智警杯备赛--机器学习算法实践

常见分类算法基础与原理

逻辑回归

概念

1.分类任务与回归任务

可以按照任务的种类,将任务分为回归任务和分类任务.那这两者的区别是什么呢?按照较官方些的说法,输入变量与输出变量均为连续变量的预测问题是回归问题,输出变量为有限个离散变量的预测问题成为分类问题

通俗一点讲，要预测的结果是一个数，比如要通过一个人的饮食预测一个人的体重，体重的值可以有无限多个，有的人50kg，有的人51kg，在50和51之间也有无限多个数.这种预测结果是某一个确定数，而具体是哪个数有无限多种可能的问题，那么可以训练出一个模型，传入参数后得到这个确定的数，这类问题称为回归问题。预测的这个变量(体重)因为有无限多种可能，在数轴上是连续的，所以称这种变量为连续变量

Logistic回归主要在流行病学中应用较多，比较常用的情形是探索某疾病的危险因素，根据危险因素预测某疾病发生的概率，等等。例如，想探讨胃癌发生的危险因素，可以选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌，即“是”或“否”，自变量就可以包括很多了，例如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的

2.逻辑回归

假设现在有一些数据点，用一条直线对这些点进行拟合（该线称为最佳拟合直线），这个拟合过程就称作回归。利用逻辑回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类。这里的“回归”一词源于最佳拟合，表示要找到最佳拟合参数集。训练分类器时的做法就是寻找最佳拟合参数，使用的是最优化算法

逻辑回归的主要用途：

• 寻找危险因素：寻找某一疾病的危险因素等；
• 预测：根据模型，预测在不同的自变量情况下，发生某病或某种情况的概率有多大；
• 判别：实际上跟预测有些类似，也是根据模型，判断某人属于某病或属于某种情况的概率有多大，也就是看一下这个人有多大的可能性是属于某病。

比如：

• 一封邮件是垃圾邮件的可能性（是、不是）
• 你购买一件商品的可能性（买、不买）
• 广告被点击的可能性（点、不点）

算法步骤

1.逻辑回归常规步骤

对于Regression问题的常规步骤为：

1. 寻找h函数（即hypothesis）；
2. 构造损失函数；
3. 想办法使得损失函数最小并求得回归参数（θ）

2.构造预测函数h

Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别），所以利用了Logistic函数（或称为Sigmoid函数），函数形式为：

hθ​(x)=g(θTx)=1+e−θTx1​

这里显示不了，函数应该是下面这个样子的

x 代表输入特征向量（比如一个人的年龄、收入等）

θ 代表模型的参数或权重，是模型需要学习的值

θTx 是一个线性组合（通常叫做线性得分或对数几率），对输入特征进行加权求和的结果，可以取任意实数

g(z) 是逻辑函数，将这个线性得分 z=θTx 作为输入，然后将其压缩到一个介于0和1之间的值，这个值可以被解释为属于某一类别的概率

e 是自然对数的底数，约等于2.71828

其中g(z)=1+e−z1​

Logistic 函数有个“S”形

横轴代表z，逻辑回归中通常是θTx

纵轴g(z)，也就是概率值

3.决策边界

如上所述，逻辑回归模型表示为：

hθ​(x)=g(θTx)=1+e−θTx1​

其中g(z)=1+e−z1​

假设阈值为0.5，

当hθ​(x)≥0.5时，y=1，当hθ​(x)<0.5时，y=0；
再次查看Logistic函数，则图则表示为

如图，当g(x)≥0.5时，z>=0

而对于hθ​(x)=g(θTx)≥0.5

则θTx≥0，此时意味着y=1

反之y=0,θTx<0

所以可以认定θTx=0

是一个决策边界，当它大于0或小于0时，逻辑回归模型分别预测不同的分类结果

逻辑回归的目标是分类，而不是预测连续值。为了将概率转化为明确的类别，需要一个决策规则。这个决策规则就是设定一个阈值（通常是0.5）

当概率 ≥ 阈值时，归为一类 (比如 1)

当概率 < 阈值时，归为另一类 (比如 0)

例如

hθ​(x)=g(θ0​+θ1​x1​+θ2​x2​)

θ0​,θ1​,θ2​分别为−3，1，1

则当−3+x1​+x2​≥0时，y=1，则x1​+x2​=3是一个线性决策边界

上述是一个线性的决策边界，当h更复杂时，需要得到一个非线性的决策边界，例如：

hθ​(x)=g(θ0​+θ1​x1​+θ2​x2​+θ3​x12​+θ4​x22​)

θ0​,θ1​,θ2​,θ3​,θ4​分别为−1，0，0，1，1

当x12​+x22​≥1时，y=1，则决策边界是一个圆形

4.损失函数

损失函数或代价函数是将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数

不同的算法常用的损失函数（Loss Function）有：

• 0-1损失函数（gold standard 标准式）

• 平方损失函数

• 绝对值损失函数

• 对数损失函数（logarithmic loss）
  主要在逻辑回归中使用，损失函数越小，模型则越好

损失函数L(Y,P(Y|X))是指样本X在分类Y的情况下，使概率P(Y|X)达到最大值。

而在逻辑回归中的损失函数使用对数损失函数定义：

Cost(hθ​(x),y)={−log(hθ​(x))−log(1−hθ​(x))​y=1y=0

逻辑回归的实现（重点）

导入算法库

from sklearn.linear_model import LogisticRegression

逻辑回归语法

class sklearn.linear_model.LogisticRegression(penalty='l2', *, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)

class sklearn.linear_model.LogisticRegression(
    penalty='l2',            # 惩罚项类型
    *,                       # 强制后续参数必须以关键字形式传递
    dual=False,              # 是否对偶或原始问题
    tol=0.0001,              # 停止优化条件的容忍度
    C=1.0,                   # 正则化强度的倒数
    fit_intercept=True,      # 是否计算截距
    intercept_scaling=1,     # 截距缩放因子
    class_weight=None,       # 类别权重
    random_state=None,       # 随机数生成器的种子
    solver='lbfgs',          # 优化算法，利用损失函数二阶导数矩阵来迭代优化损失函数                                                  （solver参数决定了对逻辑回归损失函数的优化方法，有四种）
    max_iter=100,            # 最大迭代次数
    multi_class='auto',      # 多分类策略
    verbose=0,               # 冗余模式
    warm_start=False,        # 热启动
    n_jobs=None,             # 并行运行的CPU核心数
    l1_ratio=None            # L1正则化和L2正则化的混合比 (仅当 penalty='elasticnet' 时使用)
)

liblinear：使用了坐标轴下降法来迭代优化损失函数

lbfgs：利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数

newton-cg：利用损失函数二阶导数矩阵来迭代优化损失函数

sag：随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部            分的样本来计算梯度，适合于样本数据多的时候

multi_class='auto'：多分离策略，如果选择了ovr，则4种损失函数的优化方法liblinear，newton-cg,lbfgs和sag都可以选择。但是如果选择了multinomial,则只能选择newton-cg, lbfgs和sag了

class_weight：表示分类各种类型的权重，默认不输入，即所有的分类的权重一样

                        选择‘balanced’自动根据y值计算类型权重，自己设置权重，格式：                                                  {class_label: weight}。例如0,1分类的er'yuan二元模型，设置class_weight=                                    {0:0.9, 1:0.1}，这样类型0的权重为90%，而类型1的权重为10%

max_iter=100：算法收敛最大迭代次数为100

tol=0.0001：迭代终止判断误差范围

感觉填空主要看标蓝的部分

LogisticRegression类的常用方法

fit(X, y, sample_weight=None)：拟合模型，训练LR分类器，X是训练样本，y是对应的标记向量

predict(X)：预测样本，也就是分类，X是测试集，返回array

predict_proba(X)：输出分类概率，返回每种类别的概率，按照分类类别顺序给出，如果是多分类                                 问题，multi_class="multinomial"，则会给出样本对于每种类别的概率

score(X, y, sample_weight=None)：返回给定测试集合的平均准确率，浮点型数值，对于多个分                                                              类返回，则返回每个类别的准确率组成的哈希矩阵

下面的是课程里的示例

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris#获取数据
iris = load_iris()
#数据赋值给x
X=iris.data
#数据标签赋值给y
y=iris.target
#基本数据处理， 划分数据，X是数据集，y是测试集，test_size表示测试集划分的百分比，表示测试集占数据集25%，则剩余的75%为训练集。
x_train,x_test,y_train,y_test = train_test_split(X,y,test_size=0.25)
#数据标准化，定义标准化算法对象transfer
transfer = StandardScaler()
#使用标准化算法将训练集标准化
x_train = transfer.fit_transform(x_train)
#使用标准化算法将测试集标准化
x_test = transfer.fit_transform(x_test)
# 使用逻辑回归算法，定义逻辑回归对象，其中的参数为：'liblinear'，用于优化问题的算法；l2正则化；C正则化力度
estimator = LogisticRegression(solver='liblinear',penalty='l2',C=0.1)
# 使用训练集训练逻辑回归算法，生成逻辑回归模型estimator
estimator.fit(x_train,y_train)
# 模型评估，预测测试集中数据的类别
y_predict = estimator.predict(x_test)
# 输出最终结果
print("y_predict:",y_predict)
print(y_predict==y_test)
print(estimator.score(x_test,y_test))

下面是回显

y_predict: [1 0 0 2 0 2 1 2 2 2 0 1 2 2 2 0 2 0 1 2 1 2 2 1 2 2 1 0 1 0 0 2 0 0 2 2 20]
[ True  True  True False  True  True  True  True  True  True  True  TrueTrue  True False  True  True  True  True False  True False  True  TrueFalse False  True  True False  True  True  True  True  True  True FalseTrue  True]
0.7894736842105263

线性回归算法原理

一元线性回归的实现

# -*- coding: utf-8 -*-
import numpy as np   ##科学计算库 
import scipy as sp   ##在numpy基础上实现的部分算法库
import matplotlib.pyplot as plt  ##绘图库
from scipy.optimize import leastsq  ##引入最小二乘法算法'''设置样本数据，真实数据需要在这里处理
'''
##样本数据(Xi,Yi)，需要转换成数组(列表)形式
Xi=np.array([6.19,2.51,7.29,7.01,5.7,2.66,3.98,2.5,9.1,4.2])
Yi=np.array([5.25,2.83,6.41,6.71,5.1,4.23,5.05,1.98,10.5,6.3])'''设定拟合函数和偏差函数函数的形状确定过程：1.先画样本图像2.根据样本图像大致形状确定函数形式(直线、抛物线、正弦余弦等)
'''##需要拟合的函数func :指定函数的形状
def func(p,x):k,b=preturn k*x+b##偏差函数：x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(p,x,y):return func(p,x)-y'''主要部分：附带部分说明1.leastsq函数的返回值tuple，第一个元素是求解结果，第二个是求解的代价值(个人理解)2.官网的原话（第二个值）：Value of the cost function at the solution3.实例：Para=>(array([ 0.61349535,  1.79409255]), 3)4.返回值元组中第一个值的数量跟需要求解的参数的数量一致
'''#k,b的初始值，可以任意设定,经过几次试验，发现p0的值会影响cost的值：Para[1]
p0=[1,20]#把error函数中除了p0以外的参数打包到args中(使用要求)
Para=leastsq(error,p0,args=(Xi,Yi))#读取结果
k,b=Para[0]
print("k=",k,"b=",b)
print("cost："+str(Para[1]))
print("Result linear:")
print("y="+str(round(k,2))+"x+"+str(round(b,2)))'''绘图，看拟合效果.
'''#画样本点
plt.figure(figsize=(8,6)) ##指定图像比例： 8：6
plt.scatter(Xi,Yi,color="green",label="data",linewidth=2) #画拟合直线
x=np.linspace(0,12,100) ##在0-15直接画100个连续点
y=k*x+b ##函数式
plt.plot(x,y,color="red",label="line",linewidth=2) 
plt.legend(loc='lower right') #绘制图例
plt.show()

下面是结果

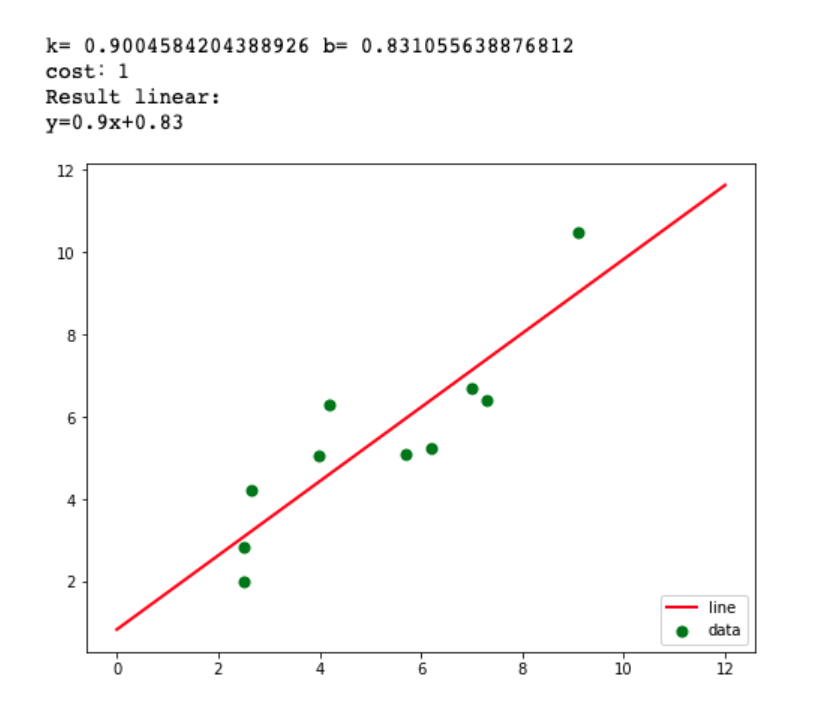
一元线性回归Sklearn实现

导入算法库

from sklearn.linear_model import LinearRegression

算法语法

class sklearn.linear_model.LinearRegression(*, fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)