基于贝叶斯网络构建结构方程_TomatoSCI分析日记
上一篇我们了解了高斯型贝叶斯网络,今天聊它的实际应用——结构方程模型(SEM)。
SEM构建时常见难题是:变量间路径如何确定?没有清晰理论假设,盲设路径容易误导。高斯贝叶斯网络能自动从数据中挖掘潜在路径,给SEM建模提供数据驱动的依据。
流程两步走:
➤ 先用贝叶斯网络探索路径结构
➤ 基于路径构建SEM,拟合评估模型
01 通过贝叶斯网络寻找路径
图1是部分数据展示,要求都要为连续变量,不能太少,当变量多而数据量少的时候,拟合的效果很差。
图2是贝叶斯网络,因为只利用它寻找路径,因此忽略系数。
图3是路径的文字表达,是接下来构建结构方程的主角。
02 结构方程拟合
图4是结构方程的可视化:
✦单向实线箭头指的是因果关系,谁影响谁,双向实线箭头是相关关系,双向虚线箭头是残差相关。
✦使用最大似然估计(ML)法估计来估算每个路径的系数,重点看变量的显著性和系数的正负号(判断正向影响和负向影响)。
✦残差相关其实就是模型未能解释的那部分之间的关系。就是即使我们建立了模型,还是有些变量之间存在着我们没能捕捉到的某些关联,这些关联表现在残差之间。
✦这是R的原始出图,非常粗糙,这里只介绍方法,美化就暂时先不做了。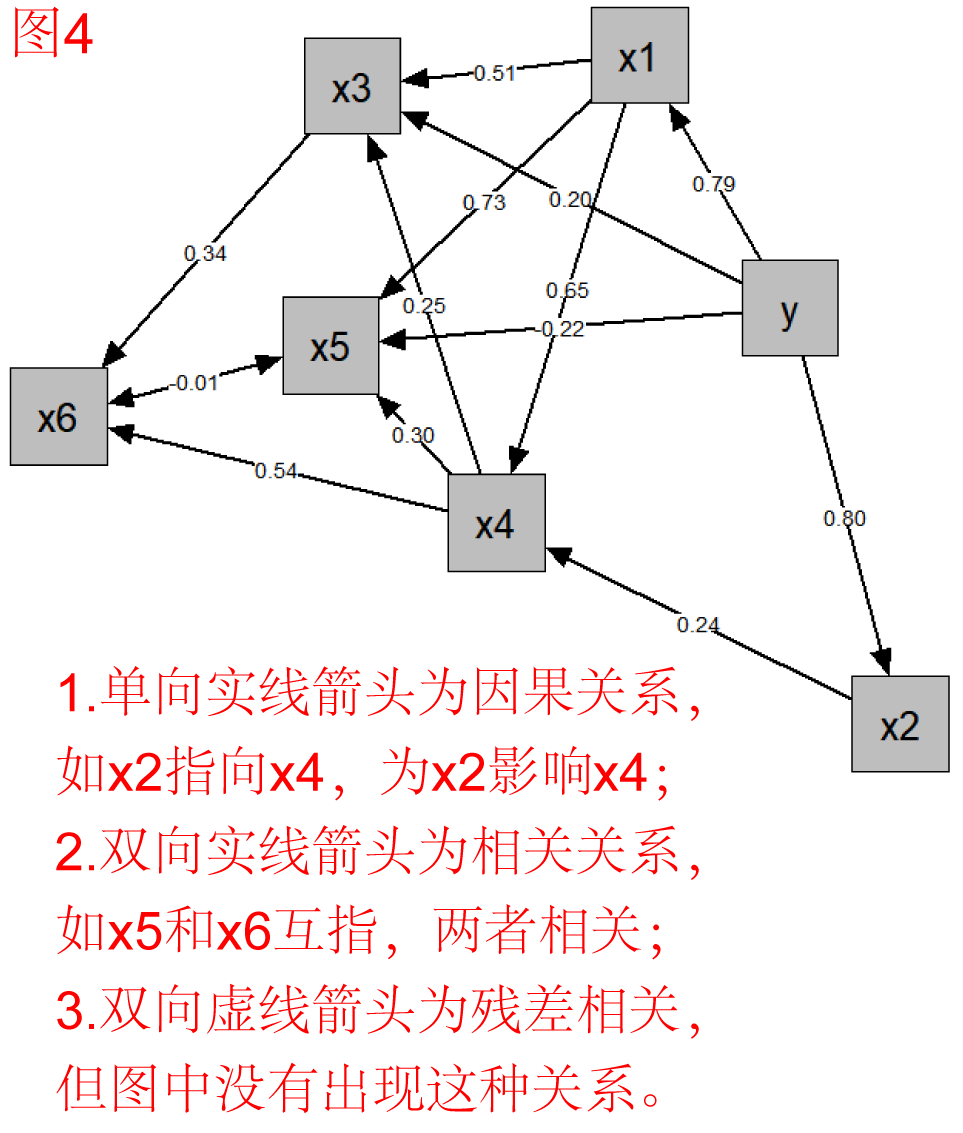
图5是结构方程拟合指标等结果:
✦P-value(Chi-square)大于0.05模型表示无显著偏差,CFI和TLI大于0.95为佳(图5A);
✦SEMR小于0.05为佳(图5B);
✦图5C的“~”匹配图中单向实线箭头的路径,表因果关系,p值小于0.05表示路径显著,系数关注正负,看正负影响;
✦图5D的“~~”匹配图中的双向实线箭头,p值和系数的理解同图5C;R方反映的是模型对因变量变化的解释程度。R²越大,说明模型越能解释因变量的变化,比如R方=0.8,意味着模型可以解释80%的因变量变化,剩下的20%是模型未能捕捉到。
03 结语
该方法优势在于,无需指定路径,对于变量间因果路径复杂的研究问题尤为适用。有潜变量的数据不适用于该方法,因为贝叶斯网络要求所有变量均为显变量。
还有一个点要避免的是,贝叶斯网络中箭头的系数只是两者之间的系数,而结构方程中箭头的系数是考虑了所有变量的系数,个人认为贝叶斯网络中的路径作为一个中间结果,我们只需关注其中变量的路径关系,系数可以不纳入分析。
TomatoSCI科研数据分析平台,欢迎大家来访!数据分析无需登录,专业在线客服答疑,还可在线传输文件,五折优惠码“tomatosci”开放使用中。PCA、RDA、PCoA、Lasso回归等方法等你就位。
