当前位置：首页 > news >正文

【数据结构】详解算法复杂度：时间复杂度和空间复杂度

news 来源：原创 2025/6/8 11:28:04

🔥个人主页：艾莉丝努力练剑

❄专栏传送门：《C语言》、《数据结构与算法》

🍉学习方向：C/C++方向

⭐️人生格言：为天地立心，为生民立命，为往圣继绝学，为万世开太平

前言：从今天开始，我们就要开始一个新篇：【数据结构与算法】啦！有诗云：“开天辟地头一篇，道轮沧海尽书言”嘛！我们之前用了34篇博客（不包括自我介绍哈）的篇幅把C语言的内容较为详细地（窃以为）给友友们介绍了一遍，我们紧接着就开始往下介绍数据结构与算法的知识点啦，数据结构与算法不分家，像算法复杂度、顺序表和链表、栈和队列、二叉树、排序这些知识点，看起来在内容上似乎没有如C语言一般多，实际上恰恰相反，这一部分内容非常丰富！大家一定要打起十二分的精神，认真学习这部分的内容！前面提到的这些知识点只是数据结构与算法内容的冰山一角（但不是说简单或者不重要，一点不简单！并且非常重要！），如同闯关游戏，由易到难，这些内容都只是初阶的数据结构知识，是往后一切大厦的根基，运输大队长（懂的友友们都知道哈）的文胆陈布雷（就是那位写出“如果战端一开，那就是地无分南北，人无分老幼，无论何人，皆有守土抗战之责任，皆应抱定牺牲一切之决心”）曾说过这么一句话喝博主这句话有异曲同工之妙：“大厦将构筑于沙丘之上”。正因如此，大家一定要认真学习数据结构与算法的内容，把基础打牢、夯实！

在C语言部分我已经向大家说明了数据结构学习需要的C语言基础：指针（一级、二级）、结构体、动态内存管理、递归（函数栈帧的创建与销毁）。大家对这几个版块如果有些陌生了话，可以去C语言专栏重温一下，专栏链接博主在每篇文章的目录下面都会附上，大家点击传送就好。

那么我们废话不多说，就从算法复杂度开始，正式进入【数据结构与算法】的内容学习！希望我的博客对友友们有所帮助！我们共同进步！

正文

一、数据结构与算法的认识

在还没有学习数据结构与算法的内容前，大抵会有友友好奇，为什么要把数据结构和算法放在一起讲，所以我们在正式学习内容之前，先来认识一下数据结构与算法的概念——

（一）数据结构

什么是数据结构？数据结构（英文名Data Structure）指的是计算机存储、组织数据（增删查改）的方式，即相互之间存在一种或多种特定关系地数组元素的集合。没有一种单一的数据结构能对所有用途都起效果，正因如此我们才要学习各种各样的数据结构，像哈希、树、图、线性表这些。

（二）算法

什么是算法呢？算法（英文名Algorithm）就是定义良好的计算过程，取一个或一组的值为输入，并产生一个或一组值作为输出，简而言之，算法就是一系列的计算步骤，用来将输入数据转化为输出结果。

比如咱们在C语言中学过的冒泡排序，就是无序的数组变成有序的数组。

注意啦，一道算法题可能存在多种思路。算法的具体实现就牵扯到本文的重点——复杂度了。

（三）总结：认识数据结构与算法的重要性

算法和数据结构是不分家的。

数据结构与算法是非常重要的一个版块，承上启下，我们现在学习初阶的数据结构不就是上承C语言，（在深入学习数据结构与算法之后——高阶数据结构）下启C++、操作系统、数据库等等相对来说学习起来十分棘手的版块。

从最近几年的趋势来看，各大厂商越来越重视对技术能力笔试，以前笔试中还分选择题、编程题，现在像深信服、美团、腾讯、科大讯飞等一票大厂的笔试都是清一色的编程题，由此可见，提升代码能力迫在眉睫，而要想写出好的代码，就要借助数据结构与算法的知识，才有可能把代码敲下来，笔试考察算法题也是可想而知，面试中一些大厂岗位实习的面试官比较看重程序员的技术水平（比如腾讯），会提问很多跟项目有关的问题，让你水也水不了，比如叫你介绍自己的项目、让你现场手撕几道算法题、考你为什么这个函数比malloc快啊诸如此类的问题。

总结：

数据结构与算法的学习没有捷径（应该说编程语言的学习本来就没有捷径可走，不然程序猿怎么还会掉头发呢？哈哈...这就是专业壁垒，也可以称为提高竞争力，二郎腿翘翘就能拿到十几个大厂offer，怎么可能呢，梦里才啥都有），还是告诉友友们两个学习的“秘诀”吧——

（1）死磕代码：敲一遍没感觉很正常，两遍、三遍、四遍...死磕，干就完了；

（2）画图！思考！——光思考是不够的，有的友友们盯着一道算法题光是看，玩君子动口不动手那套（开个玩笑），老话所谓“不动笔不读书”嘛，画图，我在介绍C语言的时候（尤其像一维数组、二维数组、指针这些）详解习题基本上都要画个图放在代码实现旁边，这样思路可能一下子就打开了，跟光思考不动笔的效果肯定不一样。

二、如何衡量算法的好坏——引入复杂度

（一）衡量算法的好坏——算法效率

在力扣(LeetCode)上面有这么一道题：轮转数组。力扣链接放这里，大家也可以试着去力扣做一做（力扣和博主以前推荐的牛客网一样，都是非常好的刷题网站，注册起来非常简单）：轮转数组

我们的思路是：循环k次将数组元素向后移动一位。

轮转一次数组元素就向后移动一位，并且保存最后一个位置的数据，我们这里用 i 表示，倒数第二位就是 i-1 ，为什么规定最后一位呢？因为如果规定第一个位置为 i ，在轮转过程中会被覆盖。

void rotate(int* nums, int numsSize, int k) 
{while (k--){int end = nums[numsSize - 1];for (int i = numsSize - 1; i > 0; i--){nums[i] = nums[i - 1];}nums[0] = end;}
}

执行和提交结果是有差异的，执行通过了提交不一定能通过，

执行一下，通过了 ——

提交一下——

这是为啥？执行可以通过，提交却通过不了，我们应该如何衡量其好坏呢？

这就要引出一个概念了，即复杂度。

算法的好与坏要从复杂度上去分析。

（二）复杂度的概念及其重要性

1、复杂度概念

算法在编写成可执行程序之后，我们运行需要耗费时间资源和空间（内存）资源，由此可见，衡量一个算法的好坏，一般是从时间和空间两个维度来衡量的，即时间复杂度和空间复杂度。

时间复杂度主要是衡量一个算法的运行快慢，而空间复杂度主要是衡量一个算法运行所需要的额外空间的大小。在计算机发展的早期，那些“大块头”计算机的存储容量很小，这时对空间复杂度才会比较在乎，近些年随着计算机行业的迅猛发展，技术日新月异，计算机的存储容量越来越大，已经达到了很高的程度，因此我们现在无需格外关注一个算法的空间复杂度了。

我们学习复杂度的重点就放在计算时间复杂度上。

2、复杂度的重要性

我们从两个角度谈谈其重要性：一个是从学习编程的角度，复杂度让程序员可以写出效率更高的代码，节省运算时间和空间；此外，从校招实习面试的考察也可以看出其作为一个考点的重要性，比如腾讯C++后台开发实习的一面曾考察“快排堆排归并时间复杂度，快排最坏的情况（上界），怎么推导的”这样一个问题。

可见，复杂度无论是作为一个学习的工具还是一个校招的考点都是非常重要的。

三、复杂度：时间复杂度和空间复杂度

（一）时间复杂度

1、时间复杂度的定义

在计算机科学中，算法的时间复杂度是用一个函数式T(N)来表示的，T(N)可以定量描述算法运行时间。既然时间复杂度是用来衡量程序的时间效率，那我们为什么不直接去计算程序的运行时间呢？其实有三个原因：

1、因为程序运行时间和编译环境、运行机器的配置都有关系，比如同一个算法程序，用一个老编译器编译和用一个新编译器编译，在相同的机器下运行时间不同；

2、同一个算法程序用一个低配置老机器运行和用一个高配置新机器运行，运行时间也不同；

3、并且这个时间只能在重新写好之后运行测试，做不到在写程序之前通过理论思想进行计算评估，故不能直接计算程序的运行时间。

程序的执行时间 = 二进制指令运行时间 * 执行次数

（假设时间是一定，是个常量）

这个T(N)函数式计算了程序的执行次数。博主在C语言专栏中有一篇文章专门介绍了编译链接，算法程序被编译后生成二进制指令，程序执行，就是CPU执行这些编译好的指令，我们通过程序代码或者说理论思想计算出程序的执行次数的函数式T(N)，假设每句指令执行时间基本一样（实际上是有差别的，只不过微乎其微可以忽略不计），执行次数和运行时间就等比例正相关，我们就可以脱离具体的编译运行环境，执行次数就可以代表程序时间效率的好坏优劣。

用T(N)这个函数式计算两个算法，出来的结果小的那个算法效率更优——

比如：A程序：T(N) = N^2，B程序：T(N) = N，B算法的效率就要优于A算法的效率。

2、T(N)函数式示例 ——引入大O渐进表示法

要求：请计算一下Func1中++count语句总共执行了多少次？

void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}
}

为什么这么化？通过这几组对比我们发现，随着N的增大，(2N + 10)对结果的影响越来越小，已经可以忽略不计，对结果影响最大的一项是N^2，故取N^2。

实际计算时间复杂度时，计算的也不是程序的精确执行次数，精确的执行次数计算起来还是很麻烦的（不同的一句程序代码，编译出的指令条数都是不一样的），计算出精确执行次数的意义不大，因为我们计算时间复杂度只是相比较算法程序的增长量级，即N不断增大时T(N)的差别，从上图我们就可以看出，N变大的过程中低位阶、常数阶对结果的影响不大（尤其N=100、1000、...之后，影响非常小），因此我们只需要计算程序能代表增长量级的大概执行次数，复杂度的表示通常使用大O的渐进表示法。

我们引入大O渐进表示法——

大O符号(Big O notation)：是用于描述函数渐进行为的数字符号：

推导大O阶规则

1、时间复杂度函数式T(N)中，只保留最高阶项，去掉那些低阶项，因为当N不断变大时，低阶项对结果影响越来越小，当N无穷大时，就可以忽略不计了；

2、如果最高阶存在且系数不是1，则去除这个项目的常数系数，因为当N不断变大，这个系数对结果影响越来越小，当N无穷大，就可以忽略不计了；

3、T(N)中如果没有N相关的项目，只有常数项，用常数1取代所有加法常数。

通过以上方法，可以得到Func1的时间复杂度为：O(N^2)。

3、示例加深巩固

示例(1)

要求：计算Func2的时间复杂度——

void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}

for循环执行2N次，while循环执行10次，这里最高阶是N^1，根据大O阶规则(2)，系数2随着N的增长对结果影响会越来越小，因此时间复杂度的结果就是O(N)。

示例(2)

要求：计算Func3的时间复杂度——

void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}

注意：T(N)函数式中的这个N是指代变量的，不是说就是N。

本题的结果其实可以进一步推理，过程已经画在图中了。

示例(3)

要求：计算Func4的时间复杂度——

void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}

执行次数只有常数项，没有N相关的项目，都用1取代所有的常数项，可能有朋友会问，如果这里这个常数项超级大，根据大O规则用1取代，不会对结果有影响吗？你的担忧没有问题，CPU计算100次和CPU计算100000000000000次时间还是有很大区别的，但是（西卡西，聪明的友友们都知道，但是后面才是重点），我在上图中画了一个坐标轴，只有常数项相当于一条直线，我们时间复杂度不是用来计算运行时间的，它是一个函数式，既然是函数式，它就是用来计算趋势的，所以如上图，随着N的变化，我们的时间没有任何变化，所以用1取代所有常数项没有问题。

示例(4)

要求：计算strchr的时间复杂度——

const char* strchr(const char* str, int character)
{const char* p_begin = s;while (*p_begin != character){if (*p_begin == '\0')return NULL;p_begin++;}return p_begin;
}

根据示例(4)我们可以总结一下：

我们发现，一些算法的时间复杂度存在最好、最坏、平均三种情况——

最坏情况：任意输入规模的最大运行次数（上界）

最好情况：任意输入规模的最小运行次数（下界）

平均情况：任意输入规模的期望运行次数

大O的渐进表示法在实际中一般情况下关注的是算法的上界，也就是最坏运行情况。

示例(5)

要求：计算BubbleSort的时间复杂度——

void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

示例(6)

要求：计算Func5的时间复杂度——

void func5(int n)
{int cnt = 1;while (cnt < n){cnt *= 2;}
}

注意对数的三种表示：

当n接近无穷大的时候，底数的大小对结果影响不大（换底公式），所以不管底数多大都可以省略不写，即写作log n，博主建议使用log n。

示例(7)

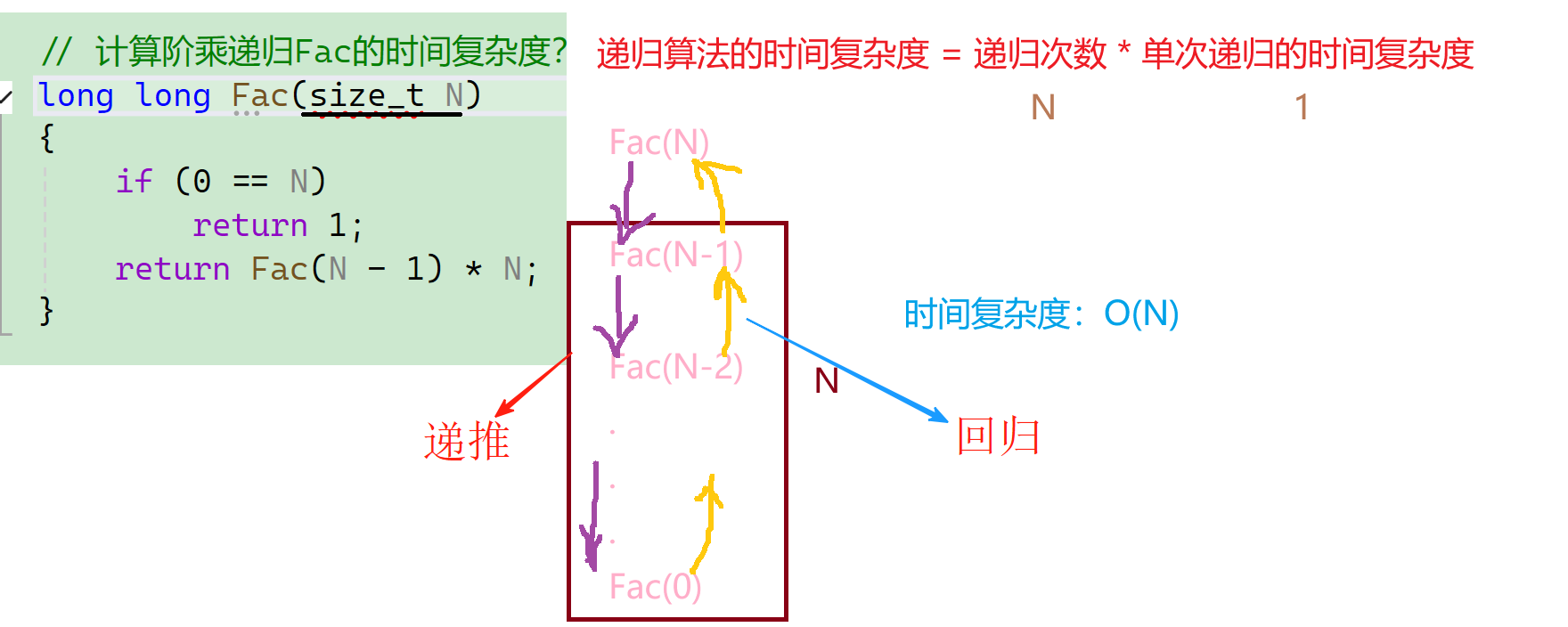
要求：计算阶乘递归Fac的时间复杂度——

long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}

（二）空间复杂度

空间复杂度也是一个数学表达式，是对一个算法在运行过程中因为算法的需要（比如在C语言动态内存管理中的malloc、calloc、realloc）需要额外临时开辟的空间。

即函数体内因实现算法而要额外开辟的空间。

void func1(int n)
{//函数体内因实现算法而需要额外开辟的空间
}

1、空间复杂度的定义

空间复杂度不是说程序占用多少字节的空间，正常情况下每个对象大小差异都不会很大，因此我们计算空间复杂度算的是变量的个数。

空间复杂度计算规则基本上和时间复杂度差不多，也是用大O渐进表示法来计算的。

注意：函数运行时所需要的栈空间（存储空间、局部变量、一些寄存器信息等）在编译期间已经确定好了，所以空间复杂度主要通过函数在运行时显式申请的额外空间来确定。

2、示例加深巩固

空间复杂度相比时间复杂度，因为计算规则差不多，只不过变成计算变量的个数，例子就少举些：

例(1)

问：计算BubbleSort的空间复杂度？

void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

我们看下面的题，只不过这次我们算的是空间复杂度：

下面划出来的就是这个算法的三个变量——

BubbleSort额外申请的空间有exchange等有限个局部变量使用了常数个额外空间。

我们知道，如果只有常数项，用常数1取代所有加法常数，这里直接算出来，是O(1)。

例(2)

计算阶乘递归Fac的空间复杂度？

long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}

递归空间复杂度 = 递归次数 * 单次递归的空间复杂度

N 1

四、复杂度（常见）的对比

下图是各个函数随n的增长其函数值的变化情况：

如下图，我们观察到：当n值增大时，时间复杂度的变化也越来越快，我们希望时间复杂度变化的慢一点，我们通过优化复杂度来优化代码。

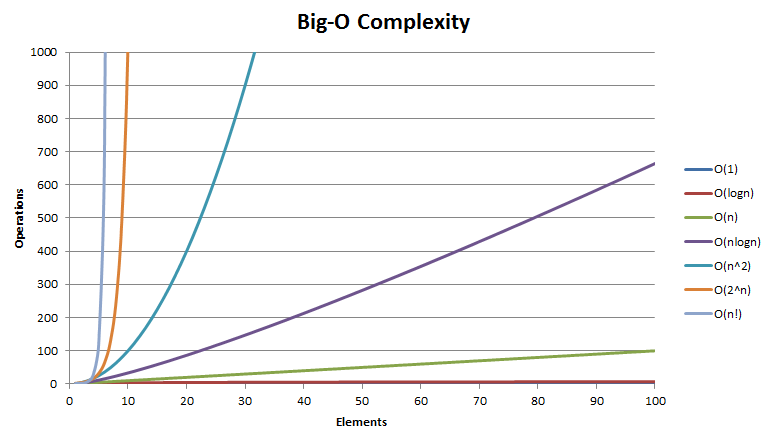
右侧的时间复杂度从上往下变化程度呈增大趋势，O(n^2)开始变化就非常夸张了。

下图是对比图：

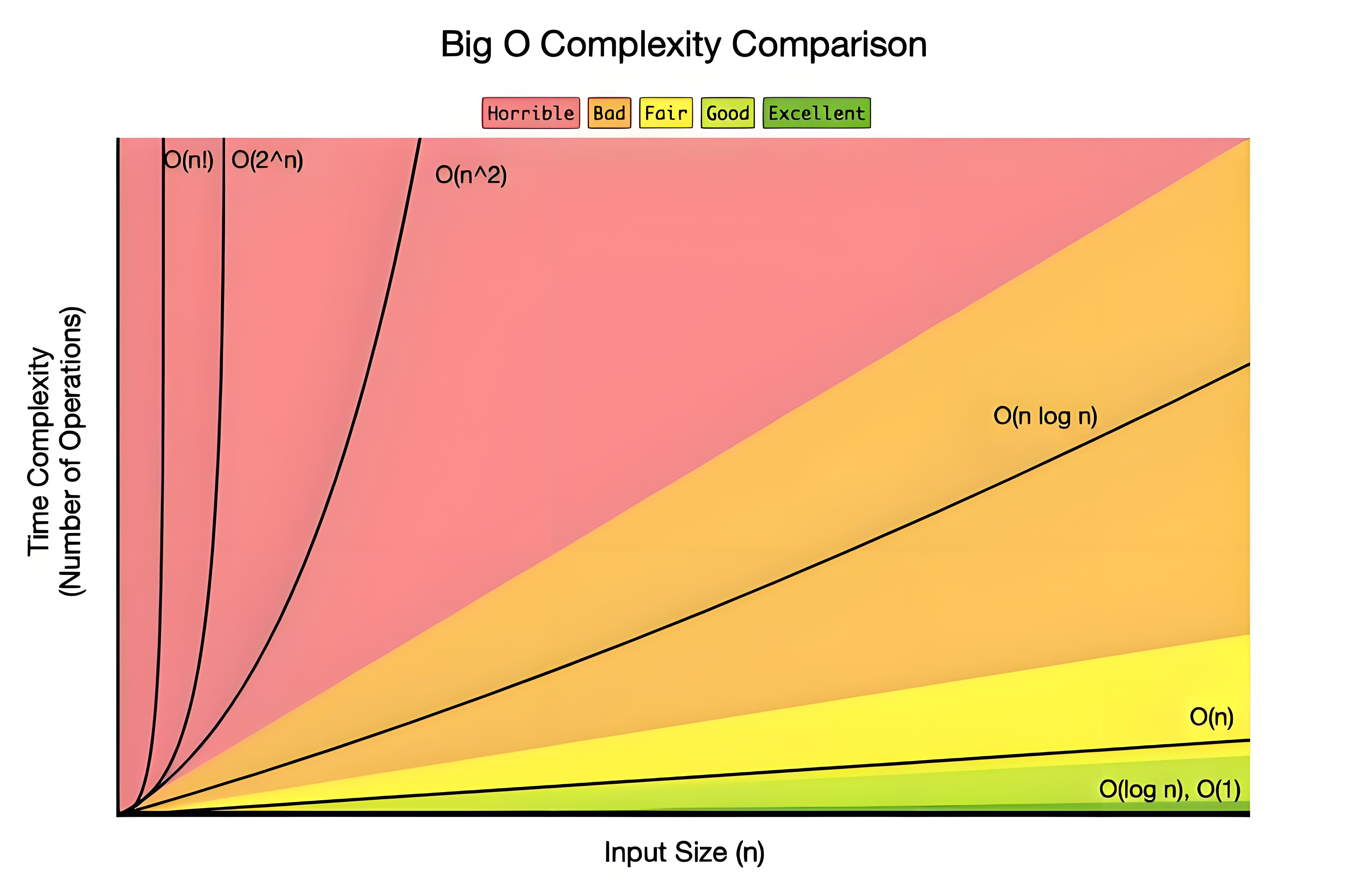
下面是各种各样的排序算法的复杂度表格：

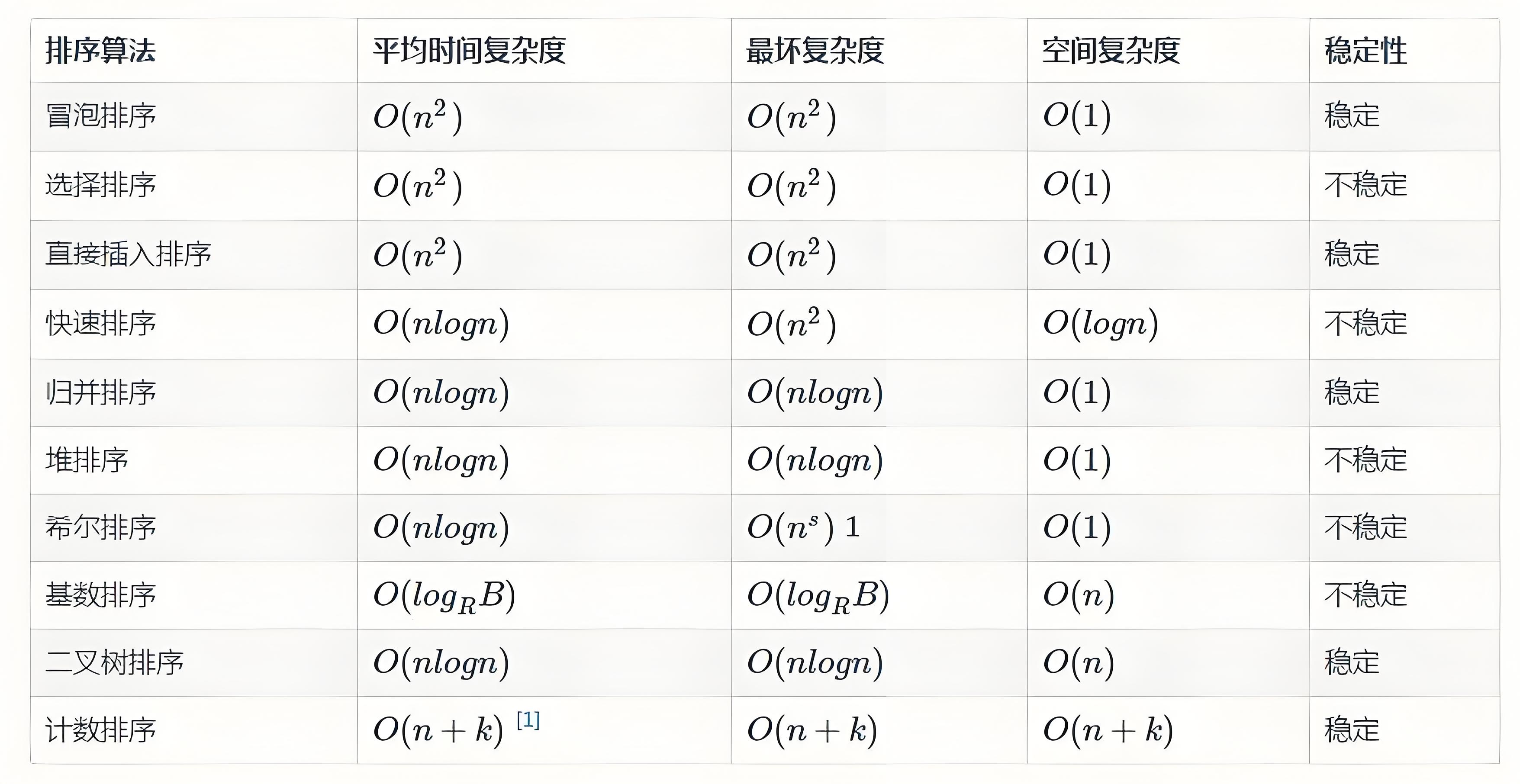
五、算法题与复杂度

回到刚才那道力扣题——旋转数组，我们刚刚的思路是循环k次将数组元素向后移动一位，我们写出来的代码运行成功了，但是提交完告诉我们“超出时间限制”，学会了大O渐进表示法，我们可以计算出用这个思路写出来的算法的时间复杂度是：O(n^2)，结合复杂度的表，我们可以发现O(n^2)那条线非常陡，O(n^2)是个不太好的复杂度，我们希望复杂度小一点。我们最开始的这个思路就是因为时间复杂度太高了，导致程序最终报错，超出了时间限制。

在讨论有没有其他思路之前，我们先看看思路(1)写出的算法的时间复杂度和空间复杂度是怎么算的，刚才我们说它的时间复杂度是O(n^2)，怎么算出来的呢？我们来看看——

k和numsSize的范围都是到10^5，嵌套循环 k * numsSize即n*n，所以时间复杂度是O(n*2)，空间复杂度是O(1)，只有一个变量。

家人们，既然本质是让时间复杂度越小越好，有没有办法把时间复杂度的“价格”打下来！有的兄弟有的，我们可以把时间复杂度变成O(N)，但是这种玩法会增加变量数，也就是说空间复杂度会增大，换言之，这是一种“空间换时间”的平衡之法，有点像端水大师哈。我们怎么做呢？

第二种思路，我们可以创建一个临时变量tmp，tmp大小和原数组一致，把原数组后k个数据依次放入tmp，再把剩下的数据依次放到tmp数组中。

//思路(2)
void rotate(int* nums, int numsSize, int k)
{//创建一个新数组tmpint tmp[numsSize];//遍历原数组，将数据轮转后放到tmp数组中for (int i = 0; i < numsSize; i++){tmp[(i + k) % numsSize] = nums[i];}//将tmp中的数据导入到nums数组for (int i = 0; i < numsSize; i++){nums[i] = tmp[i];}
}

把图像画出来（学习数据结构，一个是死磕代码，一个就是画图+思考）：

除余的好处在于不需要重复地循环就可以改数组。

这个思路的结果就是“空间换时间” ，虽然时间复杂度的确如愿以偿地降低了，但是空间复杂度增加了，虽然代码已经能圆满完成任务，但我们可不可以加大难度——不用“空间换时间”，也就是说：时间复杂度还是减小到了O(n)，但空间复杂度依旧让它为O(1)，怎么做呢？

第三种思路，我们在C语言讲过逆置，我们这里三次逆置是不是也可以实现轮转数组？

//思路(3)
//逆置
void my_reverse(int* nums, int left, int right)
{while (left < right){//交换int tmp = nums[left];nums[left] = nums[right];nums[right] = tmp;left++;right--;}
}//numsSize = 1 k=2
void rotate(int* nums, int numsSize, int k)
{k = k % numsSize;//前n-k数据逆置my_reverse(nums, 0, numsSize - k - 1);//后k个数据逆置my_reverse(nums, numsSize - k, numsSize - 1);//整体逆置my_reverse(nums, 0, numsSize - 1);
}

画图+思考：可以收获1+1>2的效果——

这样一来，不仅时间复杂度的“价格”打下来了，空间复杂度也没有增大，皆大欢喜。

轮转数组这道题有这么多思路，正体现了那句话“算法思路有很多种”。

结尾

结语：

本篇文章内容到这里就结束了，本文主要介绍了复杂度的概念，复杂度又分为时间复杂度和空间复杂度，博主相信通过本文列举的一些经典的示例和复杂度算法题的讲解，大家对复杂度已经有了更深刻的认识，可能有朋友会问：“博主，复杂度的内容光掌握这些够用吗？”大家不用担心——像博主讲的时间复杂度的内容基本上覆盖未来笔试、面试有关时间复杂度的内容考察了，只要大家掌握博主讲的这些就可以“一招鲜吃遍天”了——当然开个玩笑哈。博主的意思是大家不需要额外地再去书上啊、什么课程上挖掘了（当然对复杂度特别感兴趣的就另说了），没必要，该掌握的本文都已经覆盖到了。的的确确，像算时间复杂度不同算法的复杂度可能不一样，也有特别复杂的，但是不用担心，把本文讲的那些内容掌握就OK啦！

本期内容需要回顾的C语言知识放在下面了（指针博主写了6篇，列出来有水字数嫌疑了，就只放指针第六篇的网址，博主在指针（六）把指针部分的前五篇的网址都放在【往期回顾】了，点击【传送门】就可以去看了），大家如果对前面部分的知识点印象不深，可以去看看：

【动态内存管理】深入详解：malloc和free、calloc和realloc、常见的动态内存的错误、柔性数组、总结C/C++中程序内存区域划分

【自定义类型：结构体】：类型声明、结构体变量的创建与初始化、内存对齐、传参、位段

C语言指针深入详解（六）：sizeof和strlen的对比，【题解】数组和指针笔试题解析、指针运算笔试题解析

【深入详解】函数栈帧的创建与销毁：寄存器、压栈、出栈、调用、回收空间