C++算法训练营 Day10 栈与队列（1）

1.用栈实现队列

• LeetCode：232.用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x)将元素x推到队列的末尾
int pop()从队列的开头移除并返回元素
int peek()返回队列开头的元素
boolean empty() 如果队列为空，返回true；否则，返回false
说明：

你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty操作是合法的。
你所使用的语言也许不支持栈。你可以使用list或者deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 1：

输入：

[“MyQueue”, “push”, “push”, “peek”, “pop”, “empty”] [[], [1], [2], [],[], []]
输出： [null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1 myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

• 解题思路：

用栈来实现队列的操作时我们应该要明白，栈有一个口，而队列有两个，因此栈只能先进后出，而队列可以先进先出，因此栈需要两个才能满足队列的先进先出。

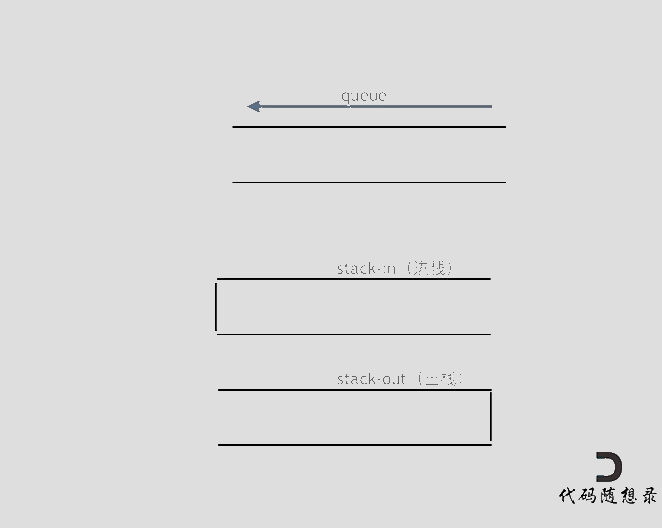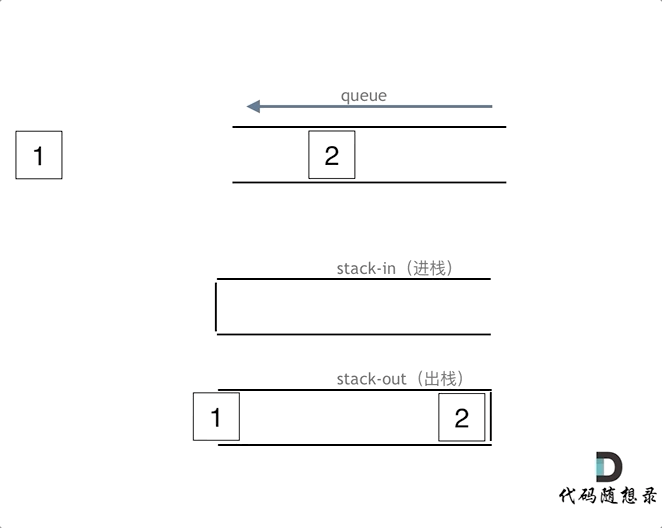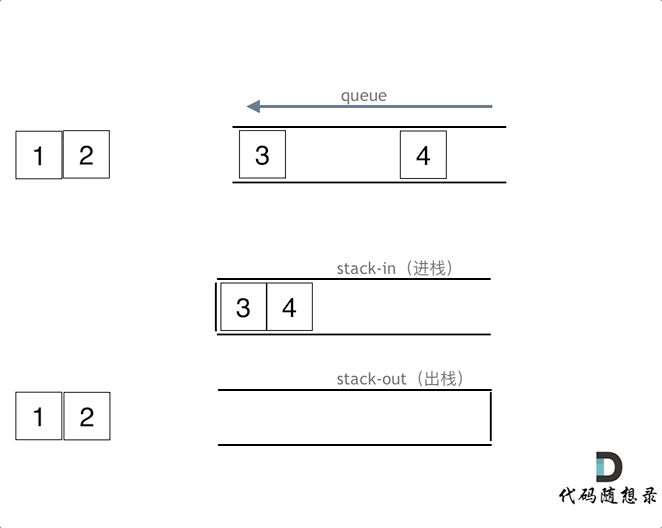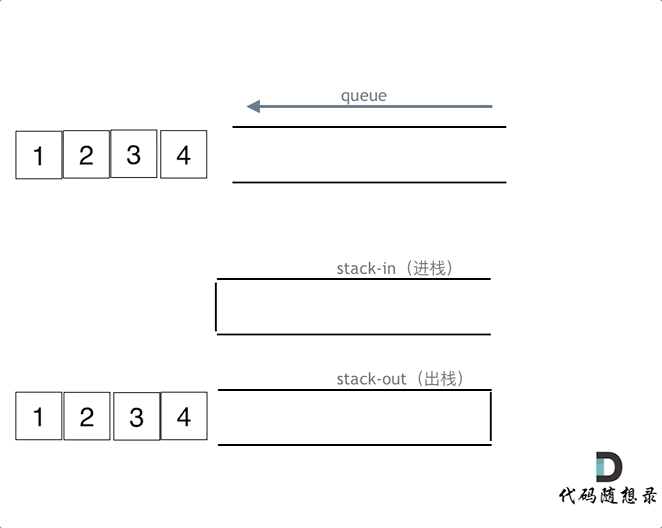
（1）push(int x)为入队操作，其时间复杂度为O(1)，可直接将新元素压入输入栈stIn，新元素总是添加到队列尾部。

 void push(int x) {stIn.push(x);}

（2）pop() 为出队操作，其平均时间复杂度为O(1)（最坏情况为O(n)），如果输出栈stOut为空，就将输入栈 stIn 所有元素转移到stOut中，然后从stOut弹出并返回栈顶元素。

 int pop() {//确保输出栈中有元素可用if (stOut.empty()) {//将输入栈的所有元素转移到输出栈（反转顺序）while(!stIn.empty()) {stOut.push(stIn.top()); //复制栈顶元素stIn.pop();             //移除输入栈顶元素}}int result = stOut.top(); //获取输出栈顶元素（队列首部）stOut.pop();              //移除输出栈顶元素return result;}

（3）peek()为查看队首函数，其平均时间复杂度为O(1)（最坏情况为O(n)），在工业级别代码开发中，最忌讳的就是实现一个类似的函数，直接把代码粘过来改一改就完事了，这样的项目代码会越来越乱，因此我们需要复用pop()获取元素，然后再将元素压回输出栈（因为peek操作不应移除元素）

int peek() {int res = this->pop(); //复用pop方法获取元素stOut.push(res);       //将元素放回输出栈（因为peek不移除元素）return res;}

其中this是一个指向当前对象的指针，在成员函数内部，可以通过this访问当前对象的所有成员。因此this->pop()等价于直接调用pop()，显式表示调用当前对象的pop成员函数。

由于peek()和pop()都需要获取队列头部元素，而pop()已经实现了：检查并转移栈元素（当stOut为空时）和返回队列头部元素，因此，不需要在peek()中重复相同的栈转移逻辑，这样写可以避免逻辑重复，也就是我们之前说的：不能直接复制粘贴过来就完事了。

（4）empty()为检查空队列函数，时间复杂度为O(1)，实现逻辑为当且仅当两个栈都为空时队列为空。

bool empty() {return stIn.empty() && stOut.empty(); //两个栈都空时队列为空}

完整代码如下：

class MyQueue {
public:stack<int> stIn;  //输入栈，用于接收新元素stack<int> stOut; //输出栈，用于队列操作//初始化队列MyQueue() {} //构造函数不需要特别操作//将元素推入队列尾部void push(int x) {stIn.push(x); //直接将新元素压入输入栈}//移除并返回队列首部元素int pop() {//确保输出栈中有元素可用if (stOut.empty()) {//将输入栈的所有元素转移到输出栈（反转顺序）while(!stIn.empty()) {stOut.push(stIn.top()); //复制栈顶元素stIn.pop();             //移除输入栈顶元素}}int result = stOut.top(); //获取输出栈顶元素（队列首部）stOut.pop();              //移除输出栈顶元素return result;}//获取队列首部元素（不移除） int peek() {int res = this->pop(); //复用pop方法获取元素stOut.push(res);       //将元素放回输出栈（因为peek不移除元素）return res;}//检查队列是否为空bool empty() {return stIn.empty() && stOut.empty(); //两个栈都空时队列为空}
};

2.用队列实现栈

• LeetCode：225.用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现MyStack类：

void push(int x)将元素x压入栈顶。
int pop()移除并返回栈顶元素。
int top()返回栈顶元素。
boolean empty()如果栈是空的，返回true；否则，返回false。

注意：

你只能使用队列的标准操作 —— 也就是push to back、peek/pop from front、size和is empty这些操作。
你所使用的语言也许不支持队列。 你可以使用list（列表）或者deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入： [“MyStack”, “push”, “push”, “top”, “pop”, “empty”] [[], [1], [2],[], [], []]
输出： [null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

• 解题思路：

由于队列是先进先出，要想实现栈的后进先出，就需要将队列前面的n - 1个元素依次重新插入队列，然后将原队尾元素出队列即可。

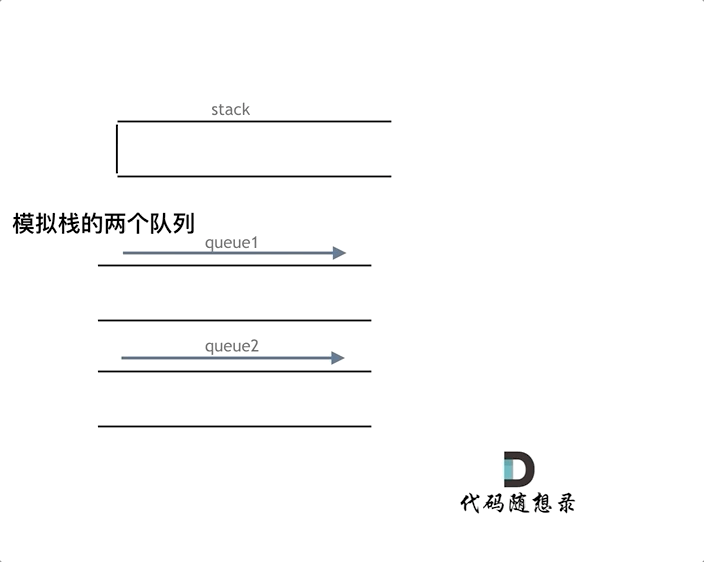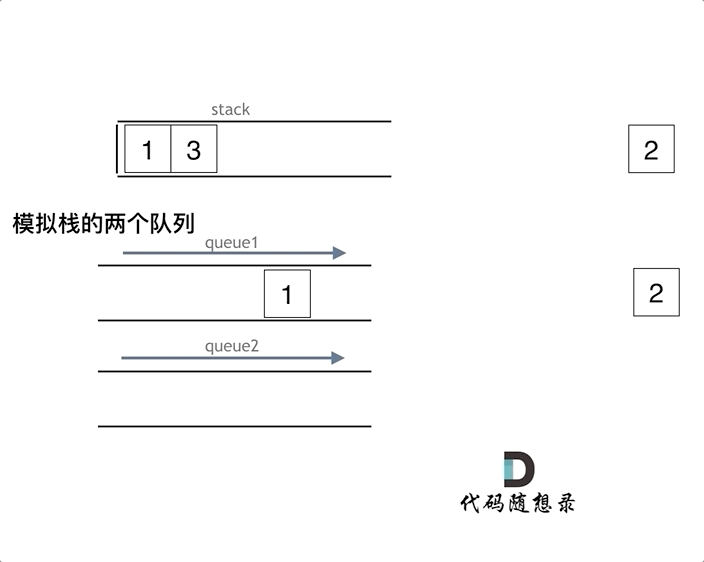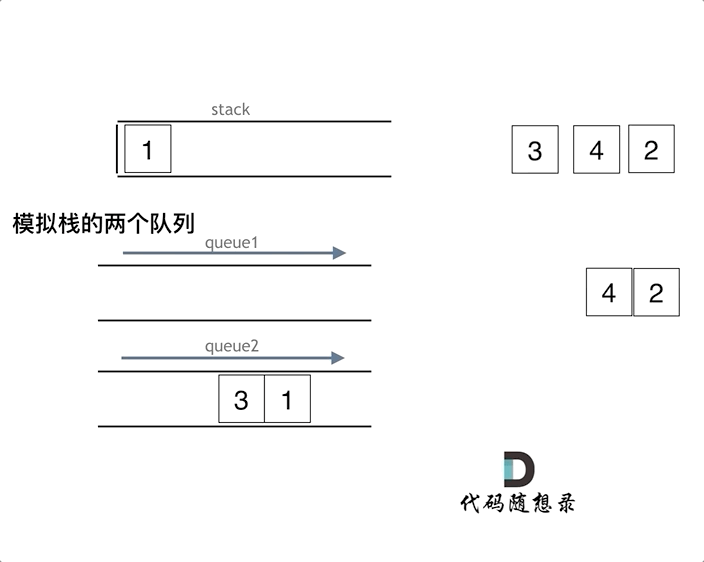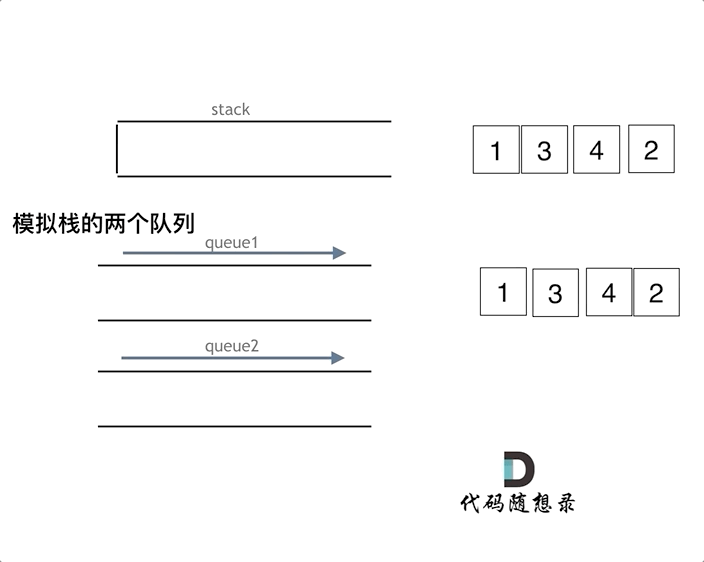
（1）push(int x) 为入栈操作，时间复杂度:为O(1)

 void push(int x) {//直接将新元素添加到队列尾部que.push(x);}

（2）pop()为出栈操作，为时间复杂度O(n)

 int pop() {//获取当前队列中元素数量int size = que.size();//我们需要保留最后一个元素作为栈顶元素//所以需要旋转 size-1 次size--;//旋转队列：将前 size-1 个元素移动到队列尾部// 样原队列的最后一个元素就会成为队列的第一个元素while (size--) {//将队首元素添加到队尾que.push(que.front());//移除原队首元素que.pop();}//此时队列的第一个元素就是栈顶元素int result = que.front();//移除栈顶元素（队列的第一个元素）que.pop();return result;}

我们来模拟一下上述代码流程：
假设我们执行三次push后调用pop，假设依次执行：

stack.push(1);
stack.push(2);
stack.push(3);
stack.pop();  // 移除并返回 3

步骤1：
初始状态（push(1), push(2), push(3) 后）
队列 que: [1, 2, 3] 1为队首, 3为队尾

步骤2：
计算旋转次数

int size = que.size();  // size = 3
size--;                 // size = 2 (需要旋转2次)

步骤3：
第一次旋转 (size=2)

que.push(que.front());  // 将队首1移到队尾 → [1,2,3,1]
que.pop();              // 移除原队首1 → [2,3,1]
// 队列状态: [2, 3, 1]

步骤4：
第二次旋转 (size=1)

que.push(que.front());  // 将队首2移到队尾 → [2,3,1,2]
que.pop();              // 移除原队首2 → [3,1,2]
// 队列状态: [3, 1, 2]

步骤5：
弹出栈顶元素

int result = que.front();   // result = 3 (栈顶元素)
que.pop();                  // 移除3 → [1, 2]
return result;              // 返回3

最终状态：
队列 que: [1, 2]
栈顶元素：2（下一次pop将返回2）

（3）top()为返回栈顶元素，其时间复杂度为O(n)，执行步骤:

1.执行与 pop() 相同的旋转操作
2.获取栈顶元素但不移除
3.恢复队列原始状态： 将栈顶元素重新加入队尾，然后移除队列头部的副本
4.返回栈顶元素

int top() {// 获取当前队列中元素数量int size = que.size();// 我们需要保留最后一个元素作为栈顶元素// 所以需要旋转 size-1 次size--;// 旋转队列：将前 size-1 个元素移动到队列尾部while (size--) {// 将队首元素添加到队尾que.push(que.front());// 移除原队首元素que.pop();}// 此时队列的第一个元素就是栈顶元素int result = que.front();// 关键步骤：为了保持栈的结构不变（因为我们只是查看栈顶元素，不是真的弹出）// 需要将栈顶元素重新放回队列尾部que.push(que.front());// 然后移除队列头部的这个元素que.pop();// 返回栈顶元素return result;}

当然，也可以写的更加简便：

int top() {int res = this -> pop();que.push(res);return res;
}

（4）empty() 为检查空栈，其时间复杂度为O(1)

 bool empty() {// 如果队列为空，则栈也为空return que.empty();}

完整代码如下：

class MyStack {
public:queue<int> que;  // 使用一个标准队列来实现栈的功能// 构造函数，不需要特殊初始化MyStack() {// 构造函数体为空，因为队列在声明时已自动初始化}// 元素入栈（压栈）操作// 时间复杂度：O(1)void push(int x) {// 直接将新元素添加到队列尾部que.push(x);}// 元素出栈（弹栈）操作// 时间复杂度：O(n)，因为需要旋转队列int pop() {// 获取当前队列中元素数量int size = que.size();// 我们需要保留最后一个元素作为栈顶元素// 所以需要旋转 size-1 次size--;// 旋转队列：将前 size-1 个元素移动到队列尾部// 这样原队列的最后一个元素就会成为队列的第一个元素while (size--) {// 将队首元素添加到队尾que.push(que.front());// 移除原队首元素que.pop();}// 此时队列的第一个元素就是栈顶元素int result = que.front();// 移除栈顶元素（队列的第一个元素）que.pop();// 返回被移除的栈顶元素return result;}// 获取栈顶元素但不移除// 时间复杂度：O(n)，因为需要旋转队列int top() {// 获取当前队列中元素数量int size = que.size();// 我们需要保留最后一个元素作为栈顶元素// 所以需要旋转 size-1 次size--;// 旋转队列：将前 size-1 个元素移动到队列尾部while (size--) {// 将队首元素添加到队尾que.push(que.front());// 移除原队首元素que.pop();}// 此时队列的第一个元素就是栈顶元素int result = que.front();// 关键步骤：为了保持栈的结构不变（因为我们只是查看栈顶元素，不是真的弹出）// 需要将栈顶元素重新放回队列尾部que.push(que.front());// 然后移除队列头部的这个元素que.pop();// 返回栈顶元素return result;}// 检查栈是否为空// 时间复杂度：O(1)bool empty() {// 如果队列为空，则栈也为空return que.empty();}
};

3.有效的括号

• LeetCode：20.有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串s，判断字符串是否有效。

有效字符串需满足：

1.左括号必须用相同类型的右括号闭合。
2.左括号必须以正确的顺序闭合。
3.每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = “()”

输出：true

示例 2：

输入：s = “()[]{}”

输出：true

示例 3：

输入：s = “(]”

输出：false

示例 4：

输入：s = “([])”

输出：true

• 解题思路：

本题的核心思想是利用栈的先进后出特性进行括号匹配，即栈非常适合做对称匹配类的题目。

（1）首先由题可知，若想括号全部匹配，必须是两两对应的，即必须为偶数，否则奇数肯定会出现不匹配的情况，因此在开始，我们要先做一个偶数的判断，其时间复杂度O(1)

if(s.size() % 2 != 0) return false;

（2）对栈进行初始化

stack<char> res;

（3）接着遍历s中的每个字符，那么在开始之前，我们先要想明白，若是不匹配会出现哪几种情况，这有利于我们书写代码的逻辑性和速度。
情况一：已经遍历完了字符串，但是栈不为空，说明没有相应的括号来匹配。

情况二：遍历字符串匹配的过程中，发现栈里没有要匹配的字符。

情况三：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号。

那么根据这三种情况就可以很快判断出是否为有效括号，接下来我们如何来解决括号的匹配问题呢？由题目可知，左括号一定是先出现的，不然先出现右括号就没有左括号与他匹配，那么根据这一点我们不难想到：

if(s[i] == '(') res.push(')');
else if(s[i] == '[') res.push(']');
else if(s[i] == '{') res.push('}');

即当我们遇到左括号时，将对应的右括号压入栈中，依次记录后续需要匹配的右括号类型。这些都完成后，我们就可以开始写判断是否为有效括号的部分了，那么（3）的整体代码如下：

for(int i = 0; i < s.size(); ++i){if(s[i] == '(') res.push(')');else if(s[i] == '[') res.push(']');else if(s[i] == '{') res.push('}');// 情况三：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号// 情况二：遍历字符串匹配的过程中，发现栈里没有我们要匹配的字符。所else if(res.empty() || s[i] != res.top()) return false;else res.pop();
}return res.empty();// 情况一：此时我们已经遍历完了字符串，若栈不为空，说明有相应的左括号没有右括号来匹配

整体代码如下所示：

class Solution {
public:bool isValid(string s) {if(s.size() % 2 != 0) return false;//如果s的长度为奇数，一定不符合要求stack<char> res;for(int i = 0; i < s.size(); ++i){if(s[i] == '(') res.push(')');else if(s[i] == '[') res.push(']');else if(s[i] == '{') res.push('}');// 第三种情况：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号 return false// 第二种情况：遍历字符串匹配的过程中，发现栈里没有我们要匹配的字符。所以return falseelse if(res.empty() || s[i] != res.top()) return false;else res.pop();}return res.empty();// 第一种情况：此时我们已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以return false，否则就return true}
}; 

4.删除字符串中的所有相邻重复项

• LeetCode：1047.删除字符串中的所有相邻重复项

给出由小写字母组成的字符串s，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在s上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入：“abbaca”
输出：“ca”
解释：
例如，在 “abbaca” 中，我们可以删除 “bb” 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 “aaca”，其中又只有 “aa” 可以执行重复项删除操作，所以最后的字符串为 “ca”。

• 解题思路

（1）初始化栈

// 1. 使用栈存储待匹配的字符
stack<char> sta;

（2）遍历字符串：若当栈空或当前字符≠栈顶元素值时，将当前字符压入栈中；若当前字符=栈顶 元素，则弹出栈顶元素，即删除重复字母对。

// 2. 遍历输入字符串for(char c : s) {// 情况1: 栈空或当前字符与栈顶不同 → 压栈if(sta.empty() || c != sta.top()) {sta.push(c);} // 情况2: 当前字符与栈顶相同 → 弹出栈顶(删除重复对)else {sta.pop();}}

（3）构建结果：将栈中剩余字符弹出，此时弹出的结果为逆序，我们需要反转操作，才能得到最终字符串。

// 3. 构建结果字符串string res = "";// 将栈中字符弹出(此时为逆序)while(!sta.empty()) {res += sta.top();sta.pop();}// 反转得到正确顺序reverse(res.begin(), res.end());return res;

运行过程如下图所示：

完整代码如下所示：

class Solution {
public:string removeDuplicates(string s) {// 1. 使用栈存储待匹配的字符stack<char> sta;// 2. 遍历输入字符串for(char c : s) {// 情况1: 栈空或当前字符与栈顶不同 → 压栈if(sta.empty() || c != sta.top()) {sta.push(c);} // 情况2: 当前字符与栈顶相同 → 弹出栈顶(删除重复对)else {sta.pop();}}// 3. 构建结果字符串string res = "";// 将栈中字符弹出(此时为逆序)while(!sta.empty()) {res += sta.top();sta.pop();}// 反转得到正确顺序reverse(res.begin(), res.end());return res;}
};