当前位置：首页 > news >正文

DFS训练（网格图）

news 来源：原创 2025/6/6 12:00:18

选自灵神题单，一、网格图DFS 。

200. 岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [["1","1","1","1","0"],["1","1","0","1","0"],["1","1","0","0","0"],["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [["1","1","0","0","0"],["1","1","0","0","0"],["0","0","1","0","0"],["0","0","0","1","1"]
]
输出：3

class Solution:def numIslands(self, grid: List[List[str]]) -> int:directions = [[0, -1], [0, 1], [1, 0], [-1, 0]]def dfs(i, j):# 若为水或者已访问则退出if grid[i][j] == "0" or visited[i][j] == True:return# 标记为已访问visited[i][j] = True# 遍历四个方向for x, y in directions:nx, ny = i + x, j + yif 0 <= nx < len(grid) and 0 <= ny < len(grid[0]):dfs(nx, ny)visited = [[False] * len(grid[0]) for _ in range(len(grid))]ans = 0  # 岛屿数量for i in range(len(grid)):for j in range(len(grid[0])):if grid[i][j] == "1" and visited[i][j] == False:dfs(i, j)ans += 1return ans

695. 岛屿的最大面积

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

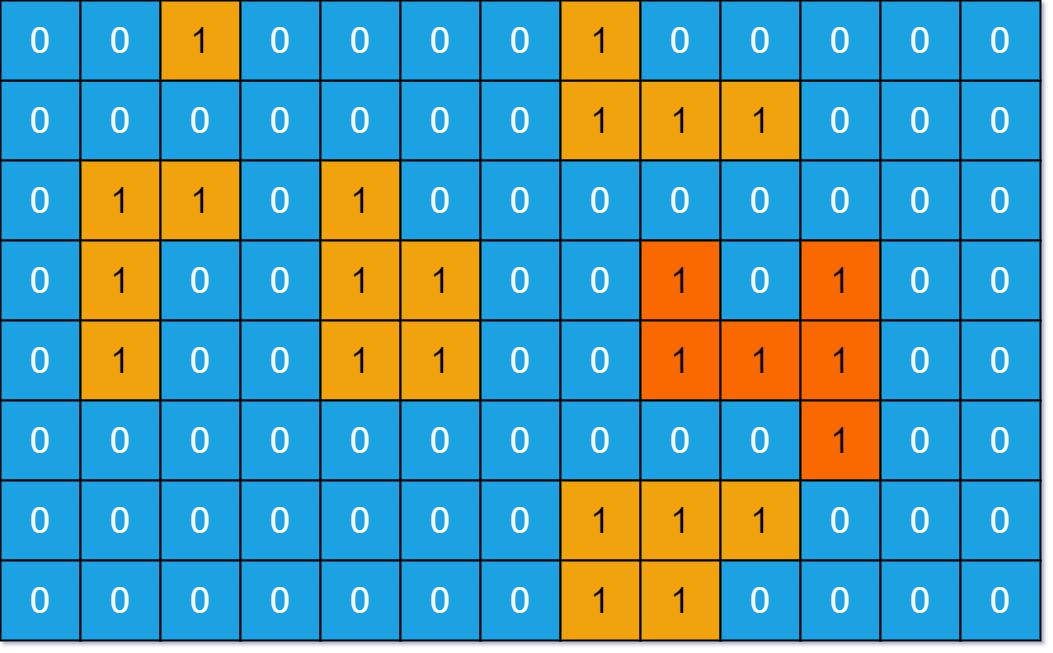
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

class Solution:def maxAreaOfIsland(self, grid: List[List[int]]) -> int:directions = [[-1, 0], [1, 0], [0, 1], [0, -1]]def dfs(i, j):nonlocal areaif grid[i][j] == 0 or visited[i][j] == True:returnarea += 1visited[i][j] = Truefor x, y in directions:nx, ny = i + x, j + yif 0 <= nx < len(grid) and 0 <= ny < len(grid[0]):dfs(nx, ny)visited = [[False] * len(grid[0]) for _ in range(len(grid))]ans = 0     # 记录最大面积for i in range(len(grid)):for j in range(len(grid[0])):area = 0dfs(i, j)ans = max(ans, area)return ans

面试题 16.19. 水域大小

你有一个用于表示一片土地的整数矩阵land，该矩阵中每个点的值代表对应地点的海拔高度。若值为0则表示水域。由垂直、水平或对角连接的水域为池塘。池塘的大小是指相连接的水域的个数。编写一个方法来计算矩阵中所有池塘的大小，返回值需要从小到大排序。

示例：

输入：
[[0,2,1,0],[0,1,0,1],[1,1,0,1],[0,1,0,1]
]
输出： [1,2,4]

class Solution:def pondSizes(self, land: List[List[int]]) -> List[int]:directions = [[-1, -1],[-1, 0],[-1, 1],[0, -1],[0, 1],[1, -1],[1, 0],[1, 1],]  # 六个方向def dfs(i, j):nonlocal areaif land[i][j] != 0 or visited[i][j] == True:returnvisited[i][j] = Truearea += 1for x, y in directions:nx, ny = i + x, j + yif 0 <= nx < len(land) and 0 <= ny < len(land[0]):dfs(nx, ny)visited = [[False] * len(land[0]) for _ in range(len(land))]ans = []for i in range(len(land)):for j in range(len(land[0])):if land[i][j] == 0 and visited[i][j] == False:area = 0  # 计算每块池塘的面积dfs(i, j)ans.append(area)ans.sort()return ans

LCS 03. 主题空间

「以扣会友」线下活动所在场地由若干主题空间与走廊组成，场地的地图记作由一维字符串型数组 grid，字符串中仅包含 "0"～"5" 这 6 个字符。地图上每一个字符代表面积为 1 的区域，其中 "0" 表示走廊，其他字符表示主题空间。相同且连续（连续指上、下、左、右四个方向连接）的字符组成同一个主题空间。

假如整个 grid 区域的外侧均为走廊。请问，不与走廊直接相邻的主题空间的最大面积是多少？如果不存在这样的空间请返回 0。

示例 1：

输入：grid = ["110","231","221"]

输出：1

解释：4 个主题空间中，只有 1 个不与走廊相邻，面积为 1。

示例 2：

输入：grid = ["11111100000","21243101111","21224101221","11111101111"]

输出：3

解释：8 个主题空间中，有 5 个不与走廊相邻，面积分别为 3、1、1、1、2，最大面积为 3。

class Solution:def largestArea(self, grid: List[str]) -> int:directions = [[-1, 0], [0, -1], [0, 1], [1, 0]]def dfs(i, j):nonlocal area, flagif visited[i][j]:returnarea += 1visited[i][j] = Truefor x, y in directions:nx, ny = i + x, j + yif 0 <= nx < len(grid) and 0 <= ny < len(grid[0]) and grid[nx][ny] == grid[i][j]:dfs(nx, ny)if nx < 0 or nx >= len(grid) or ny < 0 or ny >= len(grid[0]) or grid[nx][ny] == "0":flag = True  # 如果超出边界或者是走廊，则设置为Truevisited = [[False] * len(grid[0]) for _ in range(len(grid))]ans = 0for i in range(len(grid)):for j in range(len(grid[0])):area = 0flag = False  # 记录这个空间会不会与走廊相邻if grid[i][j] != "0" and visited[i][j] == False:dfs(i, j)if not flag:  # 如果不会相邻则记录最大空间ans = max(ans, area)return ans

463. 岛屿的周长

给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地， grid[i][j] = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

示例 1：

输入：grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出：16
解释：它的周长是上面图片中的 16 个黄色的边

示例 2：

输入：grid = [[1]]
输出：4

示例 3：

输入：grid = [[1,0]]
输出：4

class Solution:def islandPerimeter(self, grid: List[List[int]]) -> int:directions = [[-1, 0], [0, 1], [1, 0], [0, -1]]def dfs(i, j):nonlocal ansif visited[i][j]:returnvisited[i][j] = Truefor x, y in directions:nx, ny = i + x, j + y# 如果触及到网格边缘或者水域，则周长加1if nx < 0 or ny < 0 or nx >= len(grid) or ny >= len(grid[0]) or grid[nx][ny] == 0:ans += 1else:dfs(nx, ny)visited = [[False] * len(grid[0]) for _ in range(len(grid))]ans = 0for i in range(len(grid)):for j in range(len(grid[0])):if grid[i][j] == 1:dfs(i, j)break   # 由于只有一个岛屿，一次dfs后即可退出循环return ans

2658. 网格图中鱼的最大数目

给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid ，其中下标在 (r, c) 处的整数表示：

如果 grid[r][c] = 0 ，那么它是一块陆地。
如果 grid[r][c] > 0 ，那么它是一块水域，且包含 grid[r][c] 条鱼。

一位渔夫可以从任意水域格子 (r, c) 出发，然后执行以下操作任意次：

捕捞格子 (r, c) 处所有的鱼，或者
移动到相邻的水域格子。

请你返回渔夫最优策略下，最多可以捕捞多少条鱼。如果没有水域格子，请你返回 0 。

格子 (r, c) 相邻的格子为 (r, c + 1) ，(r, c - 1) ，(r + 1, c) 和 (r - 1, c) ，前提是相邻格子在网格图内。

示例 1：

输入：grid = [[0,2,1,0],[4,0,0,3],[1,0,0,4],[0,3,2,0]]
输出：7
解释：渔夫可以从格子 (1,3) 出发，捕捞 3 条鱼，然后移动到格子 (2,3) ，捕捞 4 条鱼。

示例 2：

输入：grid = [[1,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,1]]
输出：1
解释：渔夫可以从格子 (0,0) 或者 (3,3) ，捕捞 1 条鱼。

class Solution:def findMaxFish(self, grid: List[List[int]]) -> int:# 本质上是求岛屿的最大面积directions = [[-1, 0], [1, 0], [0, 1], [0, -1]]def dfs(i, j):nonlocal areaif visited[i][j] or grid[i][j] == 0:returnvisited[i][j] = Truearea += grid[i][j]for x, y in directions:nx, ny = i + x, j + yif 0 <= nx < len(grid) and 0 <= ny < len(grid[0]):dfs(nx, ny)visited = [[False] * len(grid[0]) for _ in range(len(grid))]ans = 0for i in range(len(grid)):for j in range(len(grid[0])):area = 0dfs(i, j)ans = max(ans, area)return ans

1034. 边界着色

给你一个大小为 m x n 的整数矩阵 grid ，表示一个网格。另给你三个整数 row、col 和 color 。网格中的每个值表示该位置处的网格块的颜色。

如果两个方块在任意 4 个方向上相邻，则称它们相邻。

如果两个方块具有相同的颜色且相邻，它们则属于同一个 连通分量 。

连通分量的边界 是指连通分量中满足下述条件之一的所有网格块：

在上、下、左、右任意一个方向上与不属于同一连通分量的网格块相邻
在网格的边界上（第一行/列或最后一行/列）

请你使用指定颜色 color 为所有包含网格块 grid[row][col] 的 连通分量的边界 进行着色。

并返回最终的网格 grid 。

示例 1：

输入：grid = [[1,1],[1,2]], row = 0, col = 0, color = 3
输出：[[3,3],[3,2]]

示例 2：

输入：grid = [[1,2,2],[2,3,2]], row = 0, col = 1, color = 3
输出：[[1,3,3],[2,3,3]]

示例 3：

输入：grid = [[1,1,1],[1,1,1],[1,1,1]], row = 1, col = 1, color = 2
输出：[[2,2,2],[2,1,2],[2,2,2]]

class Solution:def colorBorder(self, grid: List[List[int]], row: int, col: int, color: int) -> List[List[int]]:directions = [[-1, 0], [1, 0], [0, 1], [0, -1]]def dfs(i, j):if visited[i][j]:returnvisited[i][j] = Truefor x, y in directions:nx, ny = i + x, j + y# 如果遇到边界或者不一样的颜色，则该位置需要染色if nx < 0 or ny < 0 or nx >= len(grid) or ny >= len(grid[0]) or grid[nx][ny] != grid[i][j]:flag[i][j] = True  # 注意不能在原图上直接修改，比如说gird[i][j]=color，因为改完下次就不能判断or的最后一个条件了else:dfs(nx, ny)visited = [[False] * len(grid[0]) for _ in range(len(grid))]flag = [[False] * len(grid[0]) for _ in range(len(grid))]  # 记录需要染色的方格dfs(row, col)for i in range(len(grid)):for j in range(len(grid[0])):if flag[i][j]:grid[i][j] = colorreturn grid

1020. 飞地的数量

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次移动是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中无法在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

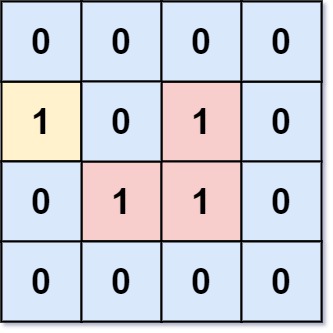
输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

示例 2：

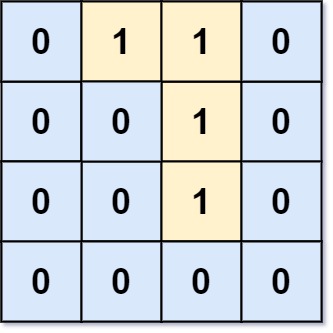
输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

class Solution:def numEnclaves(self, grid: List[List[int]]) -> int:# 题目翻译：如果没有触及到边界，则记录该岛屿面积directions = [[-1, 0], [1, 0], [0, 1], [0, -1]]def dfs(i, j):nonlocal flag, area  # 记录该岛屿有没有触及到岛屿边界if visited[i][j] or grid[i][j] == 0:returnvisited[i][j] = Truearea += 1for x, y in directions:nx, ny = i + x, j + yif nx < 0 or ny < 0 or nx >= len(grid) or ny >= len(grid[0]):flag = True  # 触及到了else:dfs(nx, ny)visited = [[False] * len(grid[0]) for _ in range(len(grid))]ans = 0for i in range(len(grid)):for j in range(len(grid[0])):flag = Falsearea = 0dfs(i, j)if flag == False:ans += areareturn ans

2684. 矩阵中移动的最大次数

给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ，矩阵由若干正整数组成。

你可以从矩阵第一列中的任一单元格出发，按以下方式遍历 grid ：

从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值严格大于当前单元格的单元格。

返回你在矩阵中能够移动的最大次数。

示例 1：

输入：grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
输出：3
解释：可以从单元格 (0, 0) 开始并且按下面的路径移动：
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
可以证明这是能够移动的最大次数。

示例 2：

输入：grid = [[3,2,4],[2,1,9],[1,1,7]]
输出：0
解释：从第一列的任一单元格开始都无法移动。

class Solution:def maxMoves(self, grid: List[List[int]]) -> int:directions = [[-1, 1], [0, 1], [1, 1]]def dfs(i, j, cnt):if visited[i][j]:returnnonlocal ansflag = Truevisited[i][j] = Truefor x, y in directions:nx, ny = i + x, j + yif nx < 0 or nx >= len(grid) or ny >= len(grid[0]):continueif grid[nx][ny] > grid[i][j]:dfs(nx, ny, cnt + 1)flag = Falseif flag:  # 如果上面的循环一次也没有进去，说明右边三个数都比当前格子小，直接记录步数ans = max(ans, cnt)ans = 0visited = [[False] * len(grid[0]) for _ in range(len(grid))]for i in range(len(grid)):dfs(i, 0, 0)return ans

1254. 统计封闭岛屿的数目

二维矩阵 grid 由 0 （土地）和 1 （水）组成。岛是由最大的4个方向连通的 0 组成的群，封闭岛是一个 完全 由1包围（左、上、右、下）的岛。

请返回 封闭岛屿 的数目。

示例 1：

输入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
输出：2
解释：
灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。

示例 2：

输入：grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
输出：1

示例 3：

输入：grid = [[1,1,1,1,1,1,1],[1,0,0,0,0,0,1],[1,0,1,1,1,0,1],[1,0,1,0,1,0,1],[1,0,1,1,1,0,1],[1,0,0,0,0,0,1],[1,1,1,1,1,1,1]]
输出：2

class Solution:def closedIsland(self, grid: List[List[int]]) -> int:directions = [[-1, 0], [1, 0], [0, 1], [0, -1]]def dfs(i, j):nonlocal flagif visited[i][j] or grid[i][j] == 1:returnvisited[i][j] = Truefor x, y in directions:nx, ny = i + x, j + yif nx < 0 or ny < 0 or nx >= len(grid) or ny >= len(grid[0]):flag = False  # 如果遇到边界了，则不是封闭岛屿else:dfs(nx, ny)visited = [[False] * len(grid[0]) for _ in range(len(grid))]ans = 0for i in range(len(grid)):for j in range(len(grid[0])):if visited[i][j] == False and grid[i][j] == 0:flag = True  # 标记该岛屿是不是封闭岛屿dfs(i, j)if flag:ans += 1return ans

130. 被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' 组成，捕获所有 被围绕的区域：

**连接：**一个单元格与水平或垂直方向上相邻的单元格连接。
区域：连接所有 'O' 的单元格来形成一个区域。
**围绕：**如果您可以用 'X' 单元格 连接这个区域，并且区域中没有任何单元格位于 board 边缘，则该区域被 'X' 单元格围绕。

通过原地将输入矩阵中的所有 'O' 替换为 'X' 来 捕获被围绕的区域。你不需要返回任何值。

示例 1：

**输入：**board = [[“X”,“X”,“X”,“X”],[“X”,“O”,“O”,“X”],[“X”,“X”,“O”,“X”],[“X”,“O”,“X”,“X”]]

输出：[[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“O”,“X”,“X”]]

解释：

在上图中，底部的区域没有被捕获，因为它在 board 的边缘并且不能被围绕。

示例 2：

**输入：**board = [[“X”]]

输出：[[“X”]]

class Solution:def solve(self, board: List[List[str]]) -> None:"""Do not return anything, modify board in-place instead."""# 标记与边缘接触的'X'单元格，然后再遍历一遍地图，如果没有被标记且为'0'的单元格则标记为'X'directions = [[-1, 0], [1, 0], [0, -1], [0, 1]]def dfs(i, j):if visited[i][j] or board[i][j] == "X":returnvisited[i][j] = Truefor x, y in directions:nx, ny = i + x, j + yif 0 <= nx < len(board) and 0 <= ny < len(board[0]):dfs(nx, ny)visited = [[False] * len(board[0]) for _ in range(len(board))]# 标记上面和下面一行for i in range(len(board)):dfs(i, 0)dfs(i, len(board[0]) - 1)# 标记左边和右边一列for j in range(len(board[0])):dfs(0, j)dfs(len(board) - 1, j)# 将未标记的未围绕区域都标记为'X'for i in range(len(board)):for j in range(len(board[0])):if visited[i][j] == False:board[i][j] = "X"

1905. 统计子岛屿

给你两个 m x n 的二进制矩阵 grid1 和 grid2 ，它们只包含 0 （表示水域）和 1 （表示陆地）。一个岛屿是由 四个方向 （水平或者竖直）上相邻的 1 组成的区域。任何矩阵以外的区域都视为水域。

如果 grid2 的一个岛屿，被 grid1 的一个岛屿完全包含，也就是说 grid2 中该岛屿的每一个格子都被 grid1 中同一个岛屿完全包含，那么我们称 grid2 中的这个岛屿为 子岛屿 。

请你返回 grid2 中 子岛屿 的数目。

示例 1：

输入：grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
输出：3
解释：如上图所示，左边为 grid1 ，右边为 grid2 。
grid2 中标红的 1 区域是子岛屿，总共有 3 个子岛屿。

示例 2：

输入：grid1 = [[1,0,1,0,1],[1,1,1,1,1],[0,0,0,0,0],[1,1,1,1,1],[1,0,1,0,1]], grid2 = [[0,0,0,0,0],[1,1,1,1,1],[0,1,0,1,0],[0,1,0,1,0],[1,0,0,0,1]]
输出：2 
解释：如上图所示，左边为 grid1 ，右边为 grid2 。
grid2 中标红的 1 区域是子岛屿，总共有 2 个子岛屿。

class Solution:def countSubIslands(self, grid1: List[List[int]], grid2: List[List[int]]) -> int:directions = [[-1, 0], [1, 0], [0, -1], [0, 1]]def dfs(i, j):nonlocal flagif visited[i][j] or grid2[i][j] == 0:returnvisited[i][j] = Trueif grid1[i][j] == 0:flag = False  # 如果岛屿1坐标相同的格子是水，岛屿2是陆地，说明不包含for x, y in directions:nx, ny = i + x, j + yif 0 <= nx < len(grid2) and 0 <= ny < len(grid2[0]):dfs(nx, ny)visited = [[False] * len(grid2[0]) for _ in range(len(grid2))]ans = 0for i in range(len(grid2)):for j in range(len(grid2[0])):if visited[i][j] == False and grid2[i][j] == 1:flag = True  # 标记当前岛屿是否被1岛屿包含dfs(i, j)if flag:ans += 1return ans

1391. 检查网格中是否存在有效路径

给你一个 m x n 的网格 grid。网格里的每个单元都代表一条街道。grid[i][j] 的街道可以是：

1 表示连接左单元格和右单元格的街道。
2 表示连接上单元格和下单元格的街道。
3 表示连接左单元格和下单元格的街道。
4 表示连接右单元格和下单元格的街道。
5 表示连接左单元格和上单元格的街道。
6 表示连接右单元格和上单元格的街道。

你最开始从左上角的单元格 (0,0) 开始出发，网格中的「有效路径」是指从左上方的单元格 (0,0) 开始、一直到右下方的 (m-1,n-1) 结束的路径。该路径必须只沿着街道走。

**注意：**你不能变更街道。

如果网格中存在有效的路径，则返回 true，否则返回 false 。

示例 1：

输入：grid = [[2,4,3],[6,5,2]]
输出：true
解释：如图所示，你可以从 (0, 0) 开始，访问网格中的所有单元格并到达 (m - 1, n - 1) 。

示例 2：

输入：grid = [[1,2,1],[1,2,1]]
输出：false
解释：如图所示，单元格 (0, 0) 上的街道没有与任何其他单元格上的街道相连，你只会停在 (0, 0) 处。

示例 3：

输入：grid = [[1,1,2]]
输出：false
解释：你会停在 (0, 1)，而且无法到达 (0, 2) 。

示例 4：

输入：grid = [[1,1,1,1,1,1,3]]
输出：true

示例 5：

输入：grid = [[2],[2],[2],[2],[2],[2],[6]]
输出：true

417. 太平洋大西洋水流问题

有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

示例 1：

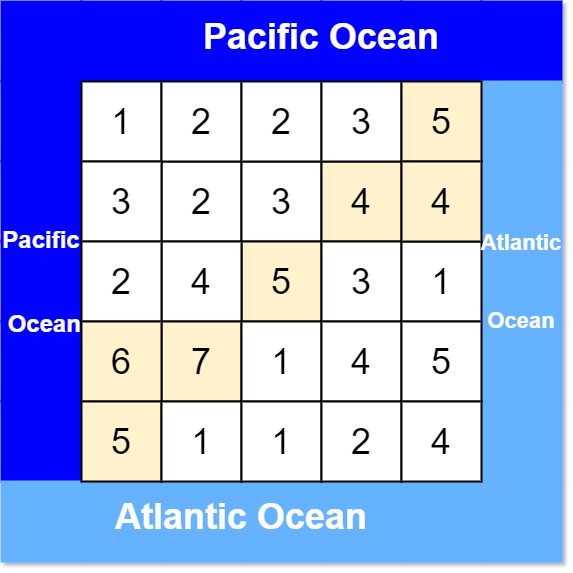
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

示例 2：

输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]

class Solution:def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:directions = [[-1, 0], [1, 0], [0, 1], [0, -1]]def dfs(i, j):nonlocal flag1, flag2if ans_flag[i][j]:flag1, flag2 = True, Truereturn  # 剪枝，如果水流到的坐标在答案中，说明一定可以留到两组边界if visited[i][j]:return# 右上角的点和左下角的点已经在两组边界边缘if i == 0 and j == len(heights[0]) - 1 or i == len(heights) - 1 and j == 0:flag1, flag2 = True, Truereturnif i == 0 or j == 0:flag1 = True  # 这里不能return或者是elif，因为还要继续判断下面的if与下面的循环if i == len(heights) - 1 or j == len(heights[0]) - 1:flag2 = Truevisited[i][j] = Truefor x, y in directions:nx, ny = i + x, j + yif 0 <= nx < len(heights) and 0 <= ny < len(heights[0]):if heights[nx][ny] <= heights[i][j]:dfs(nx, ny)ans = []ans_flag = [[False] * len(heights[0]) for _ in range(len(heights))]     # 标记答案的下标for i in range(len(heights)):for j in range(len(heights[0])):flag1, flag2 = False, False  # 标记是否流到太平洋和大西洋visited = [[False] * len(heights[0]) for _ in range(len(heights))]dfs(i, j)if flag1 and flag2:ans.append([i, j])ans_flag[i][j] = Truereturn ans

529. 扫雷游戏

让我们一起来玩扫雷游戏！

给你一个大小为 m x n 二维字符矩阵 board ，表示扫雷游戏的盘面，其中：

'M' 代表一个 未挖出的 地雷，
'E' 代表一个 未挖出的 空方块，
'B' 代表没有相邻（上，下，左，右，和所有4个对角线）地雷的 已挖出的 空白方块，
数字（'1' 到 '8'）表示有多少地雷与这块 已挖出的 方块相邻，
'X' 则表示一个 已挖出的 地雷。

给你一个整数数组 click ，其中 click = [clickr, clickc] 表示在所有 未挖出的 方块（'M' 或者 'E'）中的下一个点击位置（clickr 是行下标，clickc 是列下标）。

根据以下规则，返回相应位置被点击后对应的盘面：

如果一个地雷（'M'）被挖出，游戏就结束了- 把它改为 'X' 。
如果一个 没有相邻地雷 的空方块（'E'）被挖出，修改它为（'B'），并且所有和其相邻的 未挖出 方块都应该被递归地揭露。
如果一个 至少与一个地雷相邻 的空方块（'E'）被挖出，修改它为数字（'1' 到 '8' ），表示相邻地雷的数量。
如果在此次点击中，若无更多方块可被揭露，则返回盘面。

示例 1：

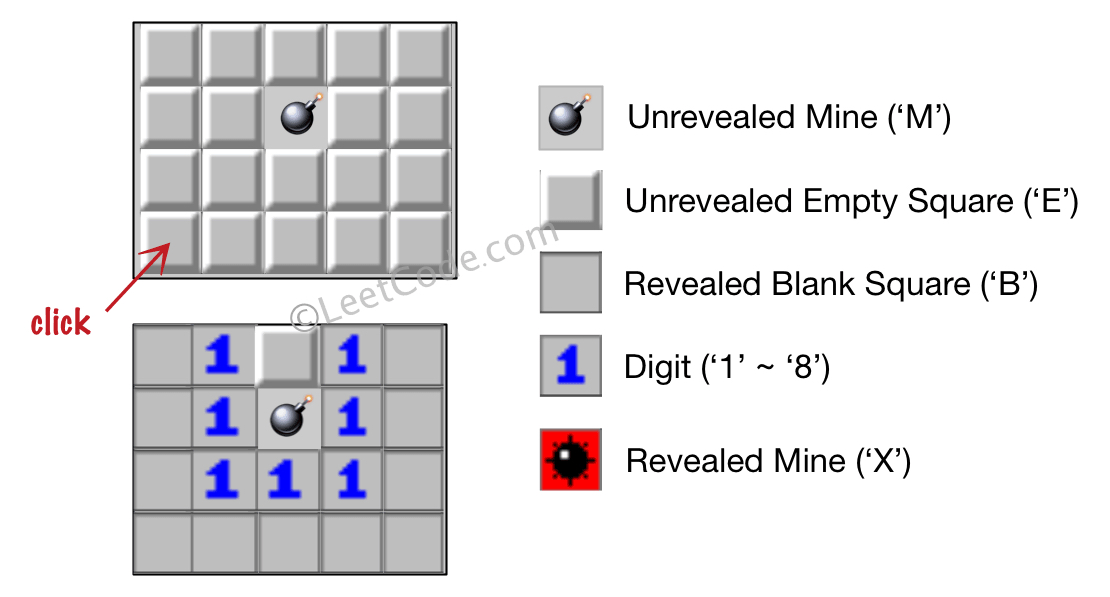
输入：board = [["E","E","E","E","E"],["E","E","M","E","E"],["E","E","E","E","E"],["E","E","E","E","E"]], click = [3,0]
输出：[["B","1","E","1","B"],["B","1","M","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]]

示例 2：

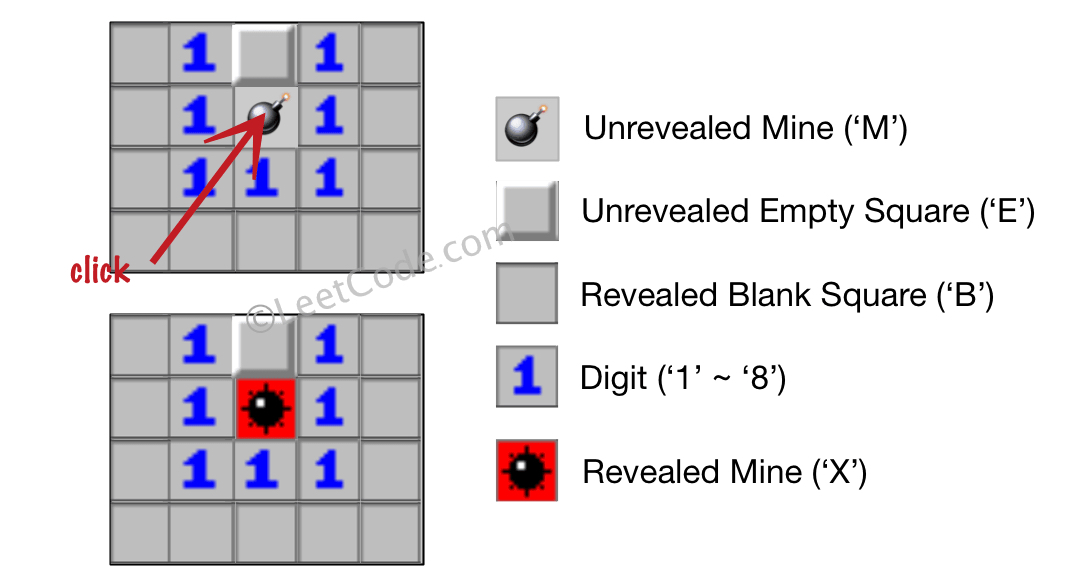
输入：board = [["B","1","E","1","B"],["B","1","M","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]], click = [1,2]
输出：[["B","1","E","1","B"],["B","1","X","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]]

1559. 二维网格图中探测环

给你一个二维字符网格数组 grid ，大小为 m x n ，你需要检查 grid 中是否存在 相同值 形成的环。

一个环是一条开始和结束于同一个格子的长度 大于等于 4 的路径。对于一个给定的格子，你可以移动到它上、下、左、右四个方向相邻的格子之一，可以移动的前提是这两个格子有 相同的值 。

同时，你也不能回到上一次移动时所在的格子。比方说，环 (1, 1) -> (1, 2) -> (1, 1) 是不合法的，因为从 (1, 2) 移动到 (1, 1) 回到了上一次移动时的格子。

如果 grid 中有相同值形成的环，请你返回 true ，否则返回 false 。

示例 1：

输入：grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]]
输出：true
解释：如下图所示，有 2 个用不同颜色标出来的环：

示例 2：

输入：grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]]
输出：true
解释：如下图所示，只有高亮所示的一个合法环：

示例 3：

输入：grid = [["a","b","b"],["b","z","b"],["b","b","a"]]
输出：false

class Solution:def containsCycle(self, grid: List[List[str]]) -> bool:directions = [[-1, 0], [1, 0], [0, -1], [0, 1]]# def dfs(i, j, ori_x, ori_y, cnt):  # 参数分别为当前坐标，原始坐标，以及步数#     nonlocal flag#     if (i,j) in visited:#         if i == ori_x and j == ori_y and cnt >= 4:#             flag = True  # 如果下一个坐标与原来坐标重合且步数大于等于4则返回#         return#     visited.add((i,j))#     for x, y in directions:#         nx, ny = i + x, j + y#         if 0 <= nx < len(grid) and 0 <= ny < len(grid[0]) and grid[nx][ny] == grid[i][j]:#             dfs(nx, ny, ori_x, ori_y, cnt + 1)#     visited.remove((i,j))  # 回溯#     if flag:#         return# visited = set()# flag = False  # 记录是否有环# for i in range(len(grid)):#     for j in range(len(grid[0])):#         dfs(i, j, i, j, 1)#         if flag:#             return True# return False# 上面的代码由于回溯，时间会超时，通过71/76# 可以将环当成一个贪吃蛇，当撞上自己的身体时，就存在环def dfs(i, j, fa_x, fa_y):  # 参数分别为当前坐标，上上一次坐标nonlocal flagif visited[i][j]:flag = Truereturnvisited[i][j] = Truefor x, y in directions:nx, ny = i + x, j + y# 下一次坐标不能是当前坐标的上一个坐标，也就是不能回头if 0 <= nx < len(grid) and 0 <= ny < len(grid[0]) and grid[nx][ny] == grid[i][j] and (nx != fa_x or ny != fa_y):dfs(nx, ny, i, j)if flag:returnvisited = [[False] * len(grid[0]) for _ in range(len(grid))]flag = False  # 记录是否有环for i in range(len(grid)):for j in range(len(grid[0])):if visited[i][j] == False:dfs(i, j, -1, -1)if flag:return Truereturn False

827. 最大人工岛

给你一个大小为 n x n 二进制矩阵 grid 。最多只能将一格 0 变成 1 。

返回执行此操作后，grid 中最大的岛屿面积是多少？

岛屿由一组上、下、左、右四个方向相连的 1 形成。

示例 1:

输入: grid = [[1, 0], [0, 1]]
输出: 3
解释: 将一格0变成1，最终连通两个小岛得到面积为 3 的岛屿。

示例 2:

输入: grid = [[1, 1], [1, 0]]
输出: 4
解释: 将一格0变成1，岛屿的面积扩大为 4。

示例 3:

输入: grid = [[1, 1], [1, 1]]
输出: 4
解释: 没有0可以让我们变成1，面积依然为 4。

class Solution:def largestIsland(self, grid: List[List[int]]) -> int:directions = [[0, 1], [0, -1], [-1, 0], [1, 0]]# 给每个岛屿编号并计算面积def dfs(i, j):nonlocal sizeif visited[i][j] or grid[i][j] != 1:returnvisited[i][j] = Truegrid[i][j] = len(area) + 2size += 1for x, y in directions:nx, ny = i + x, j + yif 0 <= nx < len(grid) and 0 <= ny < len(grid[0]):dfs(nx, ny)area = {}  # 记录岛屿的编号与面积visited = [[False] * len(grid[0]) for _ in range(len(grid))]for i in range(len(grid)):for j in range(len(grid[0])):if grid[i][j] == 1 and not visited[i][j]:size = 0dfs(i, j)area[len(area) + 2] = sizeif not area:return 1ans = max(area.values())for i in range(len(grid)):for j in range(len(grid[0])):if grid[i][j] == 0:s = set()   # 记录该水域格子上下左右的相邻岛屿有哪个for x, y in directions:nx, ny = i + x, j + yif (0 <= nx < len(grid)and 0 <= ny < len(grid[0])and grid[nx][ny] != 0):s.add(grid[nx][ny])ans = max(ans, sum(area[i] for i in s) + 1)return ans

LCP 63. 弹珠游戏

欢迎各位来到「力扣嘉年华」，接下来将为各位介绍在活动中广受好评的弹珠游戏。

N*M 大小的弹珠盘的初始状态信息记录于一维字符串型数组 plate 中，数组中的每个元素为仅由 "O"、"W"、"E"、"." 组成的字符串。其中：

"O" 表示弹珠洞（弹珠到达后会落入洞中，并停止前进）；
"W" 表示逆时针转向器（弹珠经过时方向将逆时针旋转 90 度）；
"E" 表示顺时针转向器（弹珠经过时方向将顺时针旋转 90 度）；
"." 表示空白区域（弹珠可通行）。

游戏规则要求仅能在边缘位置的 空白区域 处（弹珠盘的四角除外）沿 与边缘垂直 的方向打入弹珠，并且打入后的每颗弹珠最多能前进 num 步。请返回符合上述要求且可以使弹珠最终入洞的所有打入位置。你可以 按任意顺序 返回答案。

注意：

若弹珠已到达弹珠盘边缘并且仍沿着出界方向继续前进，则将直接出界。

示例 1：

输入： num = 4 plate = ["..E.",".EOW","..W."]

输出：[[2,1]]

解释：在 [2,1] 处打入弹珠，弹珠前进 1 步后遇到转向器，前进方向顺时针旋转 90 度，再前进 1 步进入洞中。

示例 2：

输入： num = 5 plate = [".....","..E..",".WO..","....."]

输出：[[0,1],[1,0],[2,4],[3,2]]

解释：在 [0,1] 处打入弹珠，弹珠前进 2 步，遇到转向器后前进方向逆时针旋转 90 度，再前进 1 步进入洞中。在 [1,0] 处打入弹珠，弹珠前进 2 步，遇到转向器后前进方向顺时针旋转 90 度，再前进 1 步进入洞中。在 [2,4] 处打入弹珠，弹珠前进 2 步后进入洞中。在 [3,2] 处打入弹珠，弹珠前进 1 步后进入洞中。

示例 3：

输入： num = 3 plate = [".....","....O","....O","....."]

输出：[]

解释：由于弹珠被击中后只能前进 3 步，且不能在弹珠洞和弹珠盘四角打入弹珠，故不存在能让弹珠入洞的打入位置。

class Solution:def ballGame(self, num: int, plate: List[str]) -> List[List[int]]:# 由于路径是唯一的，从出口的上下左右四个方向出发，只能对应唯一的入口# 当弹珠遇到W时，上->左->下->右->上# 当弹珠遇到E时，上->右->下->左->上dire = [[-1, 0], [0, -1], [1, 0], [0, 1]]  # 上左下右，改变方向只需取余即可# x，y表示打入区域的起始坐标，d表示发射方向# 返回的是弹珠前进的步数n, m = len(plate), len(plate[0])def dfs(x, y, d):# 如果打到边界了，返回无穷大表示不合法if x < 0 or y < 0 or x >= n or y >= m:return infc = plate[x][y]if c == ".":# 如果是空白区域，按照原方向继续飞return dfs(x + dire[d][0], y + dire[d][1], d) + 1elif c == "W":return dfs(x + dire[(d + 1) % 4][0], y + dire[(d + 1) % 4][1], (d + 1) % 4) + 1elif c == "E":return dfs(x + dire[(d + 3) % 4][0], y + dire[(d + 3) % 4][1], (d + 3) % 4) + 1else:# 遇到出口return 0ans = []# 从上下边界打入for j in range(1, m - 1):# 上边界打入的方向为 下if plate[0][j] == '.' and dfs(0, j, 2) <= num:ans.append([0, j])# 下边界打入的方向为 上if plate[n - 1][j] == '.' and dfs(n - 1, j, 0) <= num:ans.append([n - 1, j])# 从左右边界打入for i in range(1, n - 1):# 从左边界打入的方向为 右if plate[i][0] == '.' and dfs(i, 0, 3) <= num:ans.append([i, 0])# 从右边界打入的方向为 左if plate[i][m - 1] == '.' and dfs(i, m - 1, 1) <= num:ans.append([i, m - 1])return ans