当前位置：首页 > news >正文

大数据-278 Spark MLib - 基础介绍机器学习算法梯度提升树 GBDT案例详解

news 来源：原创 2025/6/6 19:19:24

点一下关注吧！！！非常感谢！！持续更新！！！

🚀 大模型与Java双线更新中！

目前《大语言模型实战》已连载至第22篇，探索 MCP 自动操作 Figma+Cursor 实现智能原型设计，持续打造实用AI工具指南！📐🤖

💻 Java篇正式开启！（300篇）

MyBatis 已完结，Spring 正在火热更新中，深入浅出助你打牢基础！

📊 大数据板块已完成多项干货更新（300篇）：

包括 Hadoop、Hive、Kafka、Flink、ClickHouse、Elasticsearch 等二十余项核心组件，覆盖离线+实时数仓全栈！

📈 GBDT 案例实战

手把手带你完成从残差计算到回归树构建与迭代训练的全过程，结合图示详细解析，最终预测精准输出！

👉 点个关注，不迷路！后续还将持续更新更多大模型+数据智能+工程实战内容，敬请期待！

在这里插入图片描述

GBDT案例

GBDT 是一种集成学习方法，全称为梯度提升决策树（Gradient Boosting Decision Tree），属于 Boosting 家族的模型。它通过多个弱学习器（通常是决策树）逐步叠加，不断优化前一次模型的预测误差，从而形成一个强学习器，常用于分类、回归等任务。

GBDT 的基本思想是：

初始化一个模型，通常预测一个常数（如均值）。
计算残差（即真实值与当前模型预测值的差值）。
训练一棵决策树来拟合这个残差。
将新树的输出加到原模型上（带上学习率系数）。
重复以上步骤，直到迭代次数达到设定值或误差足够小。

每一轮都是在减少前一轮模型的误差，而这个误差的减少过程可以看作是在目标损失函数上的梯度下降过程（所以叫“梯度”提升）。

数据介绍

根据如下数据，预测最后一个样本的身高。
在这里插入图片描述

模型训练

设置参数：
● 学习率 learning_rate = 0.1
● 迭代次数 n_trees = 5
● 树的深度 max_depth = 3

开始训练
初始化弱学习器：
在这里插入图片描述

损失函数为平方损失，因为平方损失函数是一个凸函数，直接求导，导数等于0，得到c。
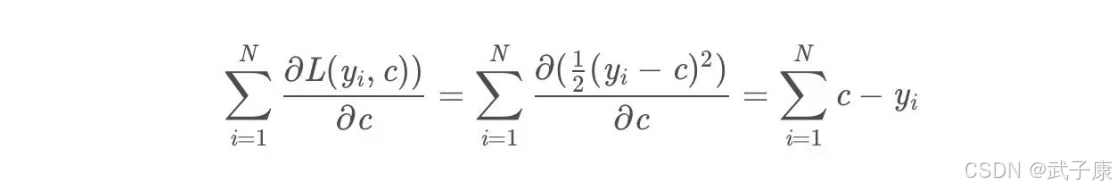
在这里插入图片描述

令导数等于0：
在这里插入图片描述

所以初始化时，c取值为所有训练样本标签的均值，c = (1.1+1.3+1.7+1.8)/4=1.475c=(1.1+1.3+1.7+1.8)/4=1.475
此时得到初始的学习率为：
f0(x) = c = 1.475

对于迭代轮数 m = 1,2…M：
由于我们设置了迭代次数，n_trees = 5, 这里 M = 5，计算负梯度，根据上文的损失函数为平方损失时，负梯度就是残差，再直白一点就是y与上一轮得到的学习器的差值：
在这里插入图片描述

残差在下表：
在这里插入图片描述
此时残差作为样本的真实值来训练弱学习器 f1(x)，即下面的数据：

接着，寻找回归树的最佳划分节点，遍历每个特征的每个可能得取值。
从年龄特征的5开始，到体重特征的70结束，分别计算分裂后两组数据的平方损失（Square Error），SEL左节点平方损失，SER右节点平方损失，找到哦啊使平方损失 SEsum = SEL + SER 最小的那个划分节点，即为最佳划分节点。

例如：
以年龄21为划分节点，将小于21的样本划分到左节点，大于21的样本划分为右节点。左节点包括x0,x1，右节点包括 x2,x3
在这里插入图片描述
以上划分点是总平方损失最小为0.025有两个划分点：年龄21和体重60，所以随机选一个作为划分点，这里我们选年龄21 现在我们的第一棵树长这个样子：

在这里插入图片描述
我们设置的参数中的树的深度 max_depth = 3，现在树的深度只有2，需要再进行一次划分，这次划分要对左右两个节点分别进行划分：

对于左节点，只含有0，1两个样本，根据下表我们选择年龄7划分：
在这里插入图片描述

对于右节点，只含有2，3两个样本，根据下表我们选择年龄30划分（也可以选体重70）：
在这里插入图片描述
现在我们第一棵树长这个样子：

此时我们树的深度满足了设置，还需要做一件事情，给这每个叶子节点分别赋一个参数Y，来你和残差
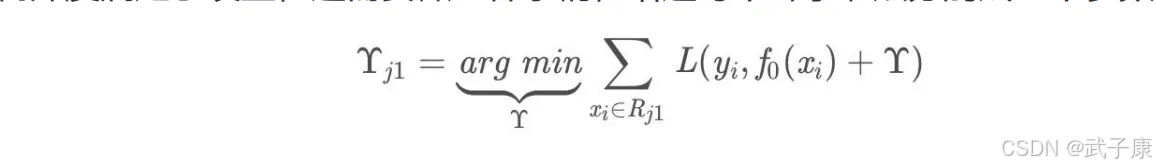
在这里插入图片描述

这里其实和上面初始化学习器是一个道理，平方损失，求导，令导数等于0，化简之后得到每个叶子节点的参数Y，其实就是标签值的值。
这个地方标签值不是原始的Y，而是本轮要拟合的标残差 y - f0(x)
根据上述划分结果，为了方便表示，规定从左到右第1,2,3,4个叶子节点：
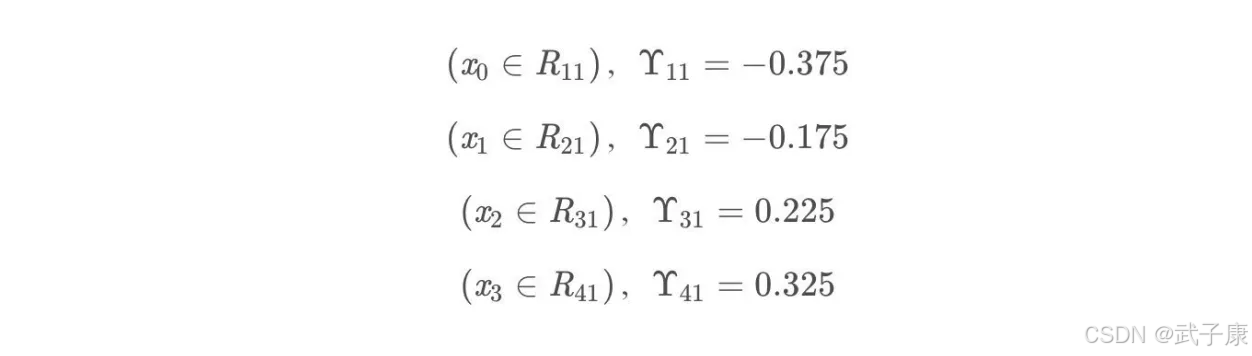
在这里插入图片描述

此时的树长这个样子：
在这里插入图片描述
此时可更新强学习器，需要用到参数学习率：learning_rate = 0.1 ，用 lr 表示：

为什么要用学习率呢？这是 Shrinkage 的思想，如果每次都全部加上（学习率为1）很容易一步学到位导致过拟合。
重复此步骤，直到 m > 5 结束，最后生成 5 棵树。
在这里插入图片描述
得到最后的强学习器：

在这里插入图片描述

预测样本

● f0(x) = 1.475
● 在f1(x)中，样本4的年龄为25，大于划分节点21岁，又小于30岁，所以被预测为 0.2250
● 在f2(x)中，样本4（省略），被预测为 0.2025
● 在f3(x)中，样本4（省略），被预测为 0.1823
● 在f4(x)中，样本4（省略），被预测为 0.1640
● 在f5(x)中，样本4（省略），被预测为 0.1476

最终预测结果：
f(x) = 1.475 + 0.1*(0.225+0.2025+0.1823+0.164+0.1476) = 1.56714