当前位置：首页 > news >正文

SVM超详细原理总结

news 来源：原创 2025/6/6 16:55:16

哈喽，我是我不是小upper~

今天想跟大家聊聊支持向量机（SVM）。很多初学者对这个算法模型特别感兴趣，它也是初学者在学习过程中非常喜爱的一种模型，更是机器学习领域中极为重要的算法之一！

今天想跟大家深入探讨一下支持向量机（SVM）的细节，咱们主要从以下几个方面来展开~

SVM 的基础内容

线性可分 SVM
- 在较为简单且理想的情况下，数据是线性可分的，也就是说，可以通过一个直线（在二维空间中）或平面（在三维空间中）等超平面，将不同类别的数据点完美地分隔开来。
- 最优超平面：我们的目标是找到这样一个超平面，它能够使得最近的数据点（我们把这些数据点称作支持向量）到超平面的距离达到最大值。在二维空间里，超平面就表现为一条直线。
- 数学表达：超平面可以用下面的方程来表示：
w⋅x+b=0
其中，w 是超平面的法向量，b 是偏置项。
- 决策规则：基于超平面，我们采用符号函数来进行分类决策，具体如下：
sign(w⋅x+b)
- 优化问题：我们的主要目标是最大化边距，这可以转化为如下的优化问题：
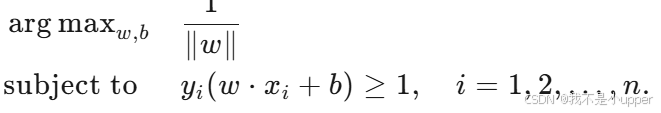
非线性 SVM 和核方法
- 然而，在现实场景中，数据往往并不是线性可分的。这时，核方法就派上用场了。核方法通过一个非线性映射，将原始特征空间映射到一个更高维的空间。在新的特征空间中，数据可能就变得线性可分了。
- 核函数：常见的核函数有多种，例如多项式核、径向基函数（RBF，也常被称为高斯核）等。
- 核函数的作用：借助核函数，我们能够在原始空间中计算出点积，而无需将数据点显式地表示在高维空间中。这大大简化了计算过程，同时也避免了高维空间带来的计算复杂度问题。
软间隔和正则化
- 在现实世界的数据中，很少有数据是完全线性可分的。因此，我们引入了软间隔的概念，允许一些数据点可以违反边距规则。
- 松弛变量：为了处理数据点的重叠和非可分情况，我们引入了松弛变量 ξi。
- 正则化参数 C：参数 C 用于控制边距的硬度以及对错误分类样本的惩罚程度，它是一个正则化参数。通过调整 C 的值，我们可以在模型的复杂度和分类准确性之间取得平衡。
优化问题（软间隔）
- 对于软间隔 SVM，优化问题转变为：

以下是对支持向量机（SVM）原理及项目实践的系统化阐述，基于技术细节展开并强化理论与代码的对应关系：

1. SVM 核心原理与数学基础

1.1 线性可分场景：硬间隔 SVM

当样本数据在特征空间中线性可分时，SVM 的目标是寻找一个最优超平面，使得不同类别数据点到超平面的几何间隔最大化。

超平面方程：在 n 维空间中，超平面由 $\mathbf{w}^T\mathbf{x} + b = 0$ 表示，其中 $\mathbf{w} = (w_1, w_2, \dots, w_n)$ 为法向量，决定超平面方向；b 为偏置项，决定超平面位置。
几何间隔：样本点 $(\mathbf{x}_i, y_i)$ 到超平面的距离为 $\frac{| \mathbf{w}^T\mathbf{x}_i + b |}{\|\mathbf{w}\|}$ ，其中 $y_i \in \{-1, +1\}$ 为类别标签。
优化目标：最大化所有样本点的最小几何间隔，等价于求解以下凸二次规划问题：该问题的解由少数关键样本点（支持向量）决定，这些点位于间隔边界上（ $y_i(\mathbf{w}^T\mathbf{x}_i + b) = 1$ ）。

1.2 非线性场景：核方法与特征空间映射

当数据在原始特征空间非线性可分时，SVM 通过核函数将样本映射到更高维的特征空间 $\mathcal{H}$ ，使数据在 $\mathcal{H}$ 中线性可分。

核函数定义：核函数 $K(\mathbf{x}_i, \mathbf{x}_j) = \phi(\mathbf{x}_i) \cdot \phi(\mathbf{x}_j)$ 表示原始空间中样本在高维空间的内积，避免了显式计算高维坐标（如 $\phi(\mathbf{x})$ 为映射函数）。
常用核函数：
- 线性核： $K(\mathbf{x}_i, \mathbf{x}_j) = \mathbf{x}_i \cdot \mathbf{x}_j$ ，适用于线性可分数据。
- 多项式核： $K(\mathbf{x}_i, \mathbf{x}_j) = (\mathbf{x}_i \cdot \mathbf{x}_j + c)^d$ ，引入多项式特征。
- 高斯核（RBF）： $K(\mathbf{x}_i, \mathbf{x}_j) = \exp(-\gamma\|\mathbf{x}_i - \mathbf{x}_j\|^2)$ ，通过参数 $\gamma$ 控制局部影响范围。

1.3 现实场景：软间隔与正则化

由于噪声和数据重叠的普遍存在，SVM 引入软间隔允许部分样本违反间隔约束，通过松弛变量 $\xi_i \geq 0$ 量化样本的 “违规程度”。

优化问题调整： $\min_{\mathbf{w}, b, \xi} \frac{1}{2}\|\mathbf{w}\|^2 + C \sum_{i=1}^m \xi_i \quad \text{s.t.} \quad y_i(\mathbf{w}^T\mathbf{x}_i + b) \geq 1 - \xi_i, \ \xi_i \geq 0$ 其中 C > 0 为正则化参数：
- C 越大，对分类错误的惩罚越强，模型复杂度越高（过拟合风险增加）；
- C 越小，允许更多分类错误，模型更倾向于最大化间隔（泛化能力增强）。

2. SVM 决策边界可视化与代码实现

2.1 二维数据决策边界绘制

以下代码基于 sklearn 实现线性 SVM 的决策边界可视化：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs# 创建 2D 数据集
X, y = make_blobs(n_samples=40, centers=2, random_state=6)# 训练 SVM 模型
clf = svm.SVC(kernel='linear', C=1000)
clf.fit(X, y)# 绘制数据点
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)# 绘制决策边界
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()# 创建网格来评估模型
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)# 绘制决策边界和边距
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])# 标记支持向量
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100, linewidth=1, facecolors='none', edgecolors='k')
plt.show()

关键逻辑：

decision_function 返回样本到超平面的有符号距离，通过等高线图可视化决策边界（Z=0）和间隔边界（Z=±1）。
支持向量为距离超平面最近的样本点，决定了超平面的位置。

2.2 三维超平面与软间隔可视化

对于三维数据，超平面为 $\mathbf{w}^T\mathbf{x} + b = 0$ ，软间隔允许样本点位于间隔内或错误分类侧。通过调整 C 可控制间隔 “硬度”，但二维代码难以直接扩展至三维，需借助投影或降维技术（如 PCA）间接可视化。

3. 鸢尾花数据集分类项目详解

3.1 数据预处理

from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaleriris = load_iris()
# 仅保留后两类数据（类别1和2）及前两个特征（简化为二维分类问题）
X_2d = iris.data[iris.target > 0, :2]
y_2d = iris.target[iris.target > 0] - 1  # 转换为0-1标签
# 标准化：使各特征均值为0、方差为1，避免尺度差异影响模型
scaler = StandardScaler()
X_2d = scaler.fit_transform(X_2d)

技术要点：

标准化是 SVM 的关键步骤，因 SVM 依赖样本间的距离计算，特征尺度差异会导致模型偏向大尺度特征。
二维化处理便于可视化，但实际应用中需保留更多特征以提升分类精度。

3.2 网格搜索与参数调优

from sklearn.model_selection import GridSearchCV, StratifiedShuffleSplit
from sklearn.svm import SVC# 定义参数网格：C（正则化强度）和gamma（RBF核参数）
C_range = np.logspace(-2, 10, 13)  # C从1e-2到1e10，共13个值
gamma_range = np.logspace(-9, 3, 13)  # gamma从1e-9到1e3，共13个值
param_grid = {'gamma': gamma_range, 'C': C_range}
# 分层交叉验证：保持类别分布均衡，5折拆分，20%数据用于验证
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=42)
grid = GridSearchCV(SVC(kernel='rbf'), param_grid, cv=cv)
grid.fit(X_2d, y_2d)

参数含义：

C：控制模型对训练数据的拟合程度，小 C 对应更宽的间隔和更强的正则化。
gamma：在 RBF 核中，控制单个样本的影响范围。小 gamma 使决策边界更平滑（泛化性强），大 gamma 导致过拟合。

3.3 决策边界与性能可视化

import matplotlib.pyplot as plt
from matplotlib.colors import Normalize# 训练不同参数组合的SVM模型
C_2d_range = [1e-2, 1, 1e2]
gamma_2d_range = [1e-1, 1, 1e1]
classifiers = [(C, gamma, SVC(C=C, gamma=gamma).fit(X_2d, y_2d)) for C in C_2d_range for gamma in gamma_2d_range]# 绘制决策边界子图
plt.figure(figsize=(8, 6))
xx, yy = np.meshgrid(np.linspace(-3, 3, 200), np.linspace(-3, 3, 200))
for k, (C, gamma, clf) in enumerate(classifiers):Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)plt.subplot(3, 3, k+1)# 绘制决策区域：-Z的色彩映射表示分类置信度plt.pcolormesh(xx, yy, -Z, cmap=plt.cm.RdBu, norm=Normalize(-1, 1))# 绘制样本点：颜色表示类别，黑色边框表示支持向量plt.scatter(X_2d[:, 0], X_2d[:, 1], c=y_2d, cmap=plt.cm.RdBu_r, edgecolors='k')plt.title(f'gamma=10^{np.log10(gamma):.0f}, C=10^{np.log10(C):.0f}')

可视化解读：

决策区域：颜色越深表示分类置信度越高，白色区域为分类边界附近（低置信度）。
参数影响：
- 当 C 固定时，增大 $\gamma$ 会使决策边界更复杂（如右下角子图出现不规则边界）。
- 当 $\gamma$ 固定时，增大 C 会缩小间隔，允许更少分类错误（如第一列子图边界更贴近样本）。

3.4 热图分析参数组合性能

scores = grid.cv_results_['mean_test_score'].reshape(len(C_range), len(gamma_range))
plt.figure(figsize=(8, 6))
# 自定义归一化：中点设为0.92，突出高分数区域
norm = MidpointNormalize(vmin=0.2, midpoint=0.92)
plt.imshow(scores, interpolation='nearest', cmap='hot', norm=norm)
plt.xlabel('gamma (log10 scale)')
plt.ylabel('C (log10 scale)')
plt.colorbar(label='Validation Accuracy')
plt.xticks(np.arange(len(gamma_range)), gamma_range.round(2), rotation=45)
plt.yticks(np.arange(len(C_range)), C_range.round(2))

性能趋势：