【拓扑】1639.拓扑排序
题目描述
这是 2018 2018 2018 年研究生入学考试中给出的一个问题:
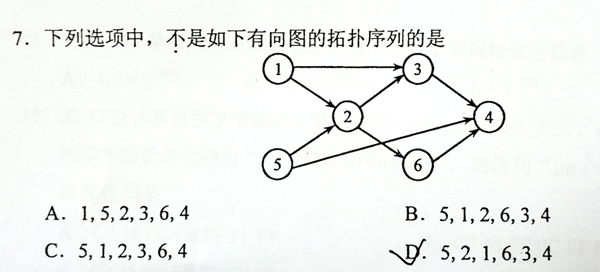
以下哪个选项不是从给定的有向图中获得的拓扑序列?
现在,请你编写一个程序来测试每个选项。
输入格式
第一行包含两个整数 N N N 和 M M M,分别表示有向图的点和边的数量。
接下来 M M M 行,每行给出一条边的起点和终点。
点的编号从 1 1 1 到 N N N。
再一行包含一个整数 K K K,表示询问次数。
接下来 K K K 行,每行包含一个所有点的排列。
一行中的数字用空格隔开。
输出格式
在一行中输出所有不是拓扑序列的询问序列的编号。
询问序列编号从 0 0 0 开始。
行首和行尾不得有多余空格,保证存在至少一个解。
数据范围
1 ≤ N ≤ 1000 1 \le N \le 1000 1≤N≤1000,
1 ≤ M ≤ 10000 1 \le M \le 10000 1≤M≤10000,
1 ≤ K ≤ 100 1 \le K \le 100 1≤K≤100
输入样例:
6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6
输出样例:
3 4
伪拓扑排序
根据序列删除结点判断下一个结点的入度是否为0
- 为 0 代表满足
- 不为 0 代表不满足条件
注意这里需要使用备份度数数组来参与每次的拓扑计算
C++ 代码
/*
根据序列删除结点判断下一个结点的入度是否为0为0 代表满足不为0 代表不满足条件
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1010, M = 10010;
int h[N],e[2*M],ne[2*M],idx;
int n,m,k;
int d[N]; // 入度
int back_d[N]; // 度数数组的备份
vector<int> temp;// 临时数组// 加边
void add(int a,int b){e[idx]=b; // 点ne[idx]=h[a]; // 边h[a]=idx++; // 指针
}// 伪拓扑排序(拿back_d去做)
bool topsort(){for(int idx=0;idx<n;idx++){// 判断当前结点的入度是否为0int cur = temp[idx];// 按序入度不为0if(back_d[cur] != 0) return false;// 削邻度for(int i=h[cur];~i;i=ne[i]){int j=e[i];// 邻居的入度必须要大于0if(back_d[j] > 0) --back_d[j];}}return true;
}int main(){cin>>n>>m;// 差点又忘了初始化h数组memset(h,-1,sizeof h);while(m--){int x,y;cin>>x>>y;add(x,y);d[y]++;}cin>>k;for(int cnt = 0 ; cnt < k ; cnt++){// 清空临时数组temp.clear(); // 或者temp.assign({})for(int i=1;i<=n;i++){int t;cin>>t;temp.push_back(t);}// 恢复度数数组// 或者 memcpy(back_d, d, n * sizeof(int)); memcpy(目标,源头,大小)for(int i=0;i<n;i++){back_d[i]=d[i];}// 拓扑排序bool ans = topsort();if(!ans){cout << cnt << " ";}}return 0;
}
