Diffusion Models: A Comprehensive Survey of Methods and Applications
CODE：2412 ACM
https://github.com/YangLing0818/Diffusion-Models-Papers-Survey-Taxonomy
Abstract
扩散模型已经成为一个强大的新深度生成模型家族，在许多应用中具有破纪录的性能，包括图像合成，视频生成和分子设计。在本调查中，我们概述了扩散模型的快速发展，将研究分为三个关键领域:有效采样，改进的似然估计和处理具有特殊结构的数据。我们还讨论了将扩散模型与其他生成模型相结合以增强结果的可能性。我们进一步回顾了扩散模型在计算机视觉、自然语言处理、时间数据建模以及其他科学学科的跨学科应用等领域的广泛应用。本调查旨在为扩散模型的状态提供一个情境化的、深入的观察，确定重点领域，并指出进一步探索的潜在领域。。
CCS概念:•计算方法→计算机视觉任务;自然语言生成;机器学习方法。
INTRODUCTION
扩散模型[111,275,280,285]已经成为最先进的深度生成模型家族。它们打破了生成对抗网络(GANs)在具有挑战性的图像合成任务中的长期统治地位[88]，并且在各种领域也显示出潜力，从计算机视觉[4,15,25,29,112,114,145,149,171,194,206,225,257,259,315,354,355,379,389]，自然语言处理[9,117,175,264,361]，时间数据建模[3,39,159,249,291,335]，多模态建模[10,243,255,258,386]，鲁棒的机器学习[23,33,144,308,357]，以及计算化学[5,115,133,166,169,196,327]和医学图像重建[31，[47-49, 53, 202, 230, 284, 328]。
已经开发了许多方法来改进扩散模型，要么通过提高经验性能[214,277,281]，要么从理论角度扩展模型的能力[187,188,279,285,371]。在过去的两年中，扩散模型的研究主体有了显著的增长，这使得新的研究人员越来越难以跟上该领域的最新发展。此外，大量的工作可能会掩盖主要趋势，阻碍进一步的研究进展。本调查旨在通过提供扩散模型研究状态的全面概述，分类各种方法，并突出关键进展来解决这些问题。我们希望这项调查能作为一个有用的切入点，为研究人员的新领域，同时提供一个更广阔的视角，为经验丰富的研究人员。
在本文中，我们首先解释了扩散模型的基础(第2节)，简要介绍了三种主要的公式:去噪扩散概率模型(ddpm)[111, 275]，基于分数的生成模型(SGMs)[280, 281]和随机微分方程(Score SDEs)[141, 279, 285]。所有这些方法的关键是用增强的随机噪声逐步扰动数据(称为“扩散”过程)，然后依次去除噪声以生成新的数据样本。我们阐明了它们是如何在相同的扩散原理下工作的，并解释了这三种模型是如何联系起来的，并且可以相互简化。
接下来，我们将对扩散模型领域的最新研究进行分类，并将其分为三个关键领域:高效采样(第3节)，改进的似然估计(第4节)，以及处理具有特殊结构的数据的方法(第5节)，例如关系数据，具有排列/旋转不变性的数据以及驻留在流形上的数据。我们通过将每个类别划分为更详细的子类别来进一步检查模型，如图图所示。此外，我们还讨论了扩散模型与其他深度生成模型的联系(第6节)，包括变分自编码器(VAEs)[156, 252]、生成对抗网络(GANs)[88]、归一化流[62,64,226,254]、自回归模型[302]和基于能量的模型(EBMs)[165, 283]。通过将这些模型与扩散模型相结合，研究人员有可能获得更强的性能。
接下来，我们的调查回顾了扩散模型在现有研究中的六个主要应用类别(第7节):计算机视觉、自然语言过程、时间数据建模、多模态学习、鲁棒的学习和跨学科应用。对于每个任务，我们提供了一个定义，描述了如何使用扩散模型来解决它，并总结了相关的先前工作。我们通过展望这一令人兴奋的新研究领域的未来可能方向来结束我们的论文(第8节和第9节)。
FOUNDATIONS OF DIFFUSION MODELS
扩散模型是一组概率生成模型，它通过注入噪声逐步破坏数据，然后学习反转这个过程来生成样本。我们在图中给出了扩散模型的直观描述。目前对扩散模型的研究主要基于三种主要的公式:去噪扩散概率模型(ddpm)[111, 214, 275]，基于分数的生成模型(SGMs)[280, 281]和随机微分方程(Score SDEs)[279, 285]。在本节中，我们将对这三个公式进行独立的介绍，同时讨论它们之间的联系。
Denoising Diffusion Probabilistic Models (DDPMs)
一种去噪扩散概率模型(DDPM)[11,275]利用了两条马尔可夫链:一条将数据扰动为噪声的正向链和一条将噪声转换回数据的反向链。前者通常是手工设计的，目的是将任何数据分布转换为简单的先验分布(例如，标准高斯分布)，而后者的马尔可夫链通过学习由深度神经网络参数化的转移核来逆转前者。通过首先从先验分布中抽样一个随机向量，然后通过反向马尔可夫链进行祖先抽样，从而生成新的数据点[158]。
先验分布（Prior Distribution）
定义：在收集数据或进行实验之前，对某个未知参数（如概率、均值等）的初始信念或假设的概率分布。
作用：反映先验知识或主观判断。例如，若认为硬币是公平的，可以选择以 p=0.5为中心的Beta分布作为先验。
后验分布（Posterior Distribution）
定义：在观测数据后，结合先验分布和似然函数更新得到的参数概率分布。
计算：通过贝叶斯定理
得出，其中：
P(θ)是先验分布，P(D∣θ)是似然函数，P(D) 是数据的边缘概率（归一化常数）。
特点：综合了先验信息和数据信息。例如，抛硬币10次得到7次正面后，若先验为Beta(1,1)，后验为Beta(8,4)，其均值接近样本比例0.7。
时间点：先验分布是数据前的初始假设，后验分布是数据后的更新结果。
影响力：先验对后验的影响取决于数据量。数据量越大，似然函数（数据）的权重越高。
应用：后验分布用于参数估计（如最大后验概率MAP）、预测和构建可信区间。
Transition Kernel 是定义马尔可夫链状态转移概率的数学工具。
对于离散状态空间，它是一个转移概率矩阵（Transition Probability Matrix），表示从当前状态转移到其他状态的概率。
对于连续状态空间，它是一个转移核函数（Transition Kernel Function），表示从当前状态转移到某个区域的概率密度。
数学表示：
设马尔可夫链的状态空间为 X，当前状态为 x，下一个状态为 y。
转移核 P(x,dy) 表示从状态 x 转移到状态 y 附近区域 dy 的概率（连续情况）或直接概率（离散情况）。
形式上，给定一个数据分布x0 ~𝑞(x0)，前向马尔可夫过程生成一个随机变量序列x1, x2…X𝑇与转换内核𝑞(X𝑡| X𝑡−1)。利用概率链式法则和马尔可夫性质，我们可以分解x1, x2，…的联合分布。X𝑇以x0为条件，记为𝑞(x1，…， x𝑇| x0)，变成
在ddpm中，我们手工制作转换内核𝑞(x𝑡| x𝑡−1)，以增量方式将数据分布𝑞(x0)转换为可处理的先验分布。过渡核的一种典型设计是高斯摄动，过渡核最常见的选择是
其中，训练前选择的超参数为:我们使用这个内核来简化这里的讨论，尽管其他类型的内核也适用于同样的方式。正如Sohl-Dickstein等人(2015)[275]所观察到的那样，这个高斯转移核允许我们将方程(1)中的联合分布边缘化，从而获得所有𝑡∈{0,1，···，𝑇}的𝑞(x𝑡| x0)的解析形式。具体来说，当设置为:
时，我们得到
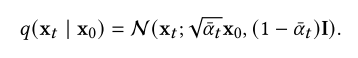
给定x0，我们可以很容易地通过对高斯向量𝝐~ N(0, I)进行采样并应用变换来获得x𝑡的样本
当𝛼𝑇≈0时，x𝑇几乎是高斯分布，因此有
直观地说，这个前向过程缓慢地向数据注入噪声，直到所有结构都丢失。为了生成新的数据样本，ddpm首先从先验分布(通常很容易获得)中生成非结构化噪声向量，然后通过在相反的时间方向上运行可学习的马尔可夫链逐渐去除其中的噪声。具体来说，反向马尔可夫链参数化为先验分布𝑝(x𝑇)= N(x𝑇;0, I)和一个可学习的转换内核𝑝(x𝑡−1 | x𝑡)。我们选择先验分布𝑝(x𝑇)= N(x𝑇;0, I)，因为正向过程是这样构造的𝑞(x𝑇)≈N(x𝑇;可学习转换内核𝑝(x𝑡−1 | x𝑡)的形式为
其中，𝜃 为模型参数，均值(χ𝑡，𝑡)和方差(χ𝑡，𝑡)用深度神经网络参数化。有了这个反向马尔可夫链，我们可以通过首先对噪声向量x𝑇~𝑝(x𝑇)进行采样来生成数据样本x0，然后从可学习的转换核x𝑡−1 ~𝑝(x𝑡−1 | x𝑡)迭代采样，直到𝑡= 1。
这个采样过程成功的关键是训练反向马尔可夫链以匹配正向马尔可夫链的实际时间反转。也就是说，我们必须调整参数𝜃，使反向马尔可夫链
的联合分布与正向过程的联合分布
非常接近。这是通过最小化两者之间的Kullback-Leibler (KL)散度来实现的:
其中(i)来自KL散度的定义，(ii)来自𝑞(x0, x1，···，x𝑇)和𝑝(x0, x1，···，x𝑇)都是分布的乘积，(iii)来自Jensen不等式。方程(8)中的第一项是数据x0的对数似然的变分下界(VLB)，这是训练概率生成模型的常见目标。我们使用“const”来表示不依赖于模型参数的常量，因此不影响优化。ddpm训练的目标是最大化负载均衡(或等效地最小化负负载均衡)，这是特别容易优化的，因为它是独立项的和，因此可以通过蒙特卡罗采样有效地估计[212]，并通过随机优化有效地优化[286]。
Ho等人(2020)[111]提出在𝐿VLB中重新加权各种项以获得更好的样本质量，并注意到在Song和Ermon[280]中，所得到的损失函数与噪声条件分数网络(ncsn)(一种基于分数的生成模型)的训练目标之间具有重要的等价性。[111]中的损失表现为
其中，𝜆(𝑡)是正权重函数，x𝑡由X0计算，𝝐由式4计算。(4)，U⟦1，𝑇⟧是集合{1，2，···，𝑇}上的均匀分布，𝝐𝜃是一个参数为𝜃的深度神经网络，它使用给定的xt和𝑡预测噪声向量𝝐。这个目标归结为等式(8)对于加权函数𝜆(𝑡)的特定选择，并且具有与基于训练分数的生成模型的多个噪声尺度上的去噪分数匹配的损失相同的形式，扩散模型的另一种公式将在下一节中讨论。
Score-Based Generative Models (SGMs)
基于分数的生成模型[280,281]的核心是(Stein)分数(又称分数或分数函数)的概念[126]。给定一个概率密度函数𝑝(x)，其分数函数定义为对数概率密度∇x log𝑝(x)的梯度。与统计学中常用的Fisher分数∇𝜃log𝑝𝜃(x)不同，这里考虑的Stein分数是数据x的函数，而不是模型参数𝜃的函数。它是一个矢量场，指向概率密度函数增长率最大的方向。
基于分数的生成模型(SGMs)[280]的关键思想是用一系列增强的高斯噪声扰动数据，并通过训练一个以噪声水平为条件的深度神经网络模型(在[280]中称为噪声条件分数网络NCSN)，共同估计所有噪声数据分布的分数函数。样本是通过使用基于分数的采样方法(包括Langevin Monte Carlo[96、137、227、280、285]、随机微分方程[136、285]、常微分方程[141、188、279、285、371]以及它们的各种组合[285])，在降低噪声水平下链接分数函数来生成的。在基于分数的生成模型中，训练和抽样是完全解耦的，因此可以在估计分数函数后使用多种抽样技术。
在2.1节中使用类似的符号，我们设𝑞(x0)为数据分布，0 <𝜎1 <𝜎2 <···< 𝜎𝑡<···<𝜎𝑇为噪声级序列。SGMs的一个典型例子涉及到通过高斯噪声分布𝑞(x𝑡| x0) = N(x𝑡;X0，𝜎𝐼)。这产生一系列噪声数据密度𝑞(x1)，𝑞(x2)，···，𝑞(x𝑇)，其中
。噪声条件分数网络是一个深度神经网络的神经网络s(x，𝑡)，用于估计分数函数∇x𝑡log𝑞(x𝑡)。从数据中学习分数函数(也就是分数估计)已经建立了分数匹配[126]、去噪分数匹配[245,246,304]和切片分数匹配[282]等技术，因此我们可以直接使用其中一种技术从扰动数据点训练我们的噪声条件分数网络。例如，使用方程(10)中的去噪分数匹配和相似的符号，则训练目标为
其中(i)由[304]导出，(ii)根据假设𝑞(x𝑡|x0)=N(x𝑡；x0，𝜎i)，以及(iii)根据x𝑡=x0+𝜎𝑡𝝐这一事实。同样，我们用𝜆(𝑡表示)正权重函数，并且“const”不依赖于可训练参数𝜃的常量。比较等式(14)和等式(10)，一旦我们设置了𝝐𝜃(x，𝑡)=−𝜎𝑡S𝜃(x，𝑡)，显然DDPM和SGM的培养目标是等价的。此外，还可以将分数匹配推广到更高阶。数据密度的高阶导数提供了关于数据分布的附加局部信息。孟等人[209]提出了一种广义去噪得分匹配方法来有效估计高阶得分函数。该模型可以提高朗之万动力学的混合速度，从而提高扩散模型的采样效率。
对于样本生成，SGMs利用迭代方法从s个S𝜃(x，𝑇)、S𝜃(x，𝑇−1)、···、S𝜃(x, 0)中依次生成样本。由于SGMs中训练和推理的解耦，存在许多采样方法，其中一些将在下一节中讨论。在这里，我们介绍了sgm的第一种采样方法，称为退火朗格万动力学(ALD)[280]。设为每个时间步长的迭代次数，𝑠𝑡> 0为步长。我们首先用x𝑇~ N(0, I)初始化ALD，然后对𝑡=𝑇，𝑇−1，····，1依次应用朗格万蒙特卡罗。在每个时间步长0≤𝑡<𝑇时，从x(0)𝑡= x(N)𝑡+1开始，然后根据以下更新规则进行迭代:
朗格万-蒙特卡罗理论[227]保证了当𝑠𝑡→0和二进制操作N→∞时，x(N)0成为数据分布𝑞(x0)的有效样本。
Stochastic Differential Equations (Score SDEs)随机微分方程
ddpm和SGMs可以进一步推广到无限时间步长或噪声水平的情况，其中扰动和去噪过程是随机微分方程(SDEs)的解。我们将此公式称为Score SDE[285]，因为它利用SDE进行噪声扰动和样本生成，而去噪过程需要估计噪声数据分布的分数函数。
SDE通过以下随机微分方程(SDE)控制的扩散过程将数据扰动为噪声[285]:
式中，f(x，𝑡)和𝑔(𝑡)为SDE的扩散和漂移函数，w为标准维纳过程(即布朗运动)。ddpm和SGMs中的前向过程都是SDE的离散化。Song et al.(2020)[285]表明，对于ddpm，对应的SDE为:
其中，当𝑇趋于无穷大时
，对于SGMs，对应的SDE为
其中，当𝑇趋于无穷时，𝜎(𝑡/𝑇)= 𝜎𝑡。这里我们使用𝑞𝑡(x)来表示x𝑡在正向过程中的分布。
至关重要的是，对于方程(15)形式的任何扩散过程，Anderson[6]表明可以通过求解以下逆时SDE来反转它:
其中¯w是时间向后流动时的标准维纳过程，d𝑡表示无穷小的负时间步长。这种反向SDE的解轨迹与正向SDE的解轨迹具有相同的边际密度，只是它们在相反的时间方向上演化[285]。直观地说，反时SDE的解决方案是逐渐将噪声转换为数据的扩散过程。此外，Song et al.(2020)[285]证明了常微分方程(ODE)的存在性，即概率流ODE，其轨迹与逆时SDE具有相同的边际。概率流ODE为:
逆时SDE和概率流ODE都允许从相同的数据分布中采样，因为它们的轨迹具有相同的边际。
一旦每个时间步t的分数函数∇x log𝑞𝑡(x)已知，我们就可以解锁逆时SDE (方程(18))和概率流ODE (方程(19))，并随后通过使用各种数值技术(如退火朗格万动力学[280](参见第2.2节)、数值SDE求解器[136,285]、数值ODE求解器[141,188,277,285,371]，以及预测校正方法(mcmc和数值ODE/SDE求解器的组合)[285]。与SGMs一样，我们通过将方程(14)中的分数匹配目标推广到连续时间，将时间相关的分数模型s (x𝑡，𝑡)参数化来估计分数函数，从而得到以下目标:
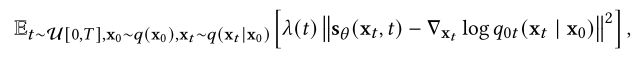
其中U[0，𝑇]表示[0，𝑇]上的均匀分布，其余的符号遵循方程(14)。
扩散模型的后续研究主要从三个主要方向改进这些经典方法(ddpm、SGMs和Score SDEs):更快更有效的采样，更准确的似然和密度估计，以及处理具有特殊结构的数据(如排列不变性、流形结构和离散数据)。在接下来的三节(第3节至第5节)中，我们对每个方向进行了广泛的调查。在表1中，我们在连续和离散时间设置下列出了三种类型的扩散模型，并进行了更详细的分类，以及相应的文章和年份。
DIFFUSION MODELS WITH EFFICIENT SAMPLING
从扩散模型中生成样本通常需要涉及大量评估步骤的迭代方法。最近的大量工作集中在加快采样过程的同时也提高了所得样品的质量。我们将这些有效的采样方法分为两大类:不涉及学习的(无学习采样)和在训练扩散模型后需要额外学习过程的(基于学习的采样)。
Learning-Free Sampling
扩散模型的许多采样器依赖于离散方程(18)中的逆时SDE或方程(19)中的概率流ODE。由于采样成本随着离散时间步数的增加而成比例地增加，许多研究人员致力于开发既减少时间步数又使离散误差最小化的离散化方案。
SDE Solvers.
DDPM的产生过程[11,275]可以看作是逆时SDE的特定离散化。如2.3节所述，DDPM的正向过程将方程(16)中的SDE离散化，其对应的反向SDE为
Song等人(2020)[285]表明，方程(5)定义的反向马尔可夫链相当于方程(21)的数值SDE求解器。
噪声条件分数网络(NCSNs)[280]和临界阻尼朗格万扩散(CLD)[66]都是从朗格万动力学中得到灵感来解决逆时SDE问题的。特别是，ncsn利用退火朗格万动力学(ALD，参见第2.2节)迭代生成数据，同时平滑地降低噪声水平，直到生成的数据分布收敛到原始数据分布。虽然ALD的采样轨迹不是逆时SDE的精确解，但它们具有正确的边际，因此在假设Langevin动力学在每个噪声水平收敛到平衡状态下产生正确的样本。一致退火采样(CAS)[137]进一步改进了ald方法，这是一种基于分数的MCMC方法，具有更好的时间步长缩放和添加的噪声。受统计力学的启发，CLD提出了一个带有辅助速度项的增广SDE，类似于欠阻尼朗格万扩散。为了获得扩展SDE的时间反转，CLD只需要学习给定数据的速度条件分布的分数函数，可以说比直接学习数据的分数更容易。据报道，增加的速度项提高了采样速度和质量。
[285]中提出的反向扩散方法对逆时SDE的离散化方法与正向扩散方法相同。对于正向SDE的任何一步离散化，可以写出一般形式如下:
其中，z~N(0, I)、fi和gi由SDE的漂移/扩散系数和离散化方案决定。反向扩散建议将逆时SDE离散化，类似于正时SDE，即
其中，s为训练后的噪声条件分数模型。Song等人(2020)[285]证明了反向扩散法是方程(18)中逆时SDE的数值求解器。该过程可应用于任何类型的正向sde，经验结果表明，对于称为VP-SDE的特定类型的sde，该采样器的性能略好于DDPM[285]。
Jolicoeur-Martineau等人(2021)[136]开发了一种具有自适应步长的SDE求解器，以更快地生成。通过比较高阶SDE求解器的输出与低阶SDE求解器的输出来控制步长。在每个时间步，高阶和低阶求解器分别从前一个样本x '𝑝𝑟𝑒𝑣生成新的样本x ' high和x ' low。然后通过比较两个样本之间的差异来调整步长。如果x ' high和x ' low相似，算法将返回x ' high，然后增加步长。x ' high和x ' low之间的相似性可以通过以下方式来衡量:
式中𝛿(x ' low, x ' prev) := max(𝜖𝑎𝑏𝑠, 𝜖𝑟𝑒𝑙 max(|x ' low|，|x ' prev|) )，以及𝜖𝑎𝑏𝑠, 𝜖𝑟𝑒𝑙为绝对公差和相对公差。
[285]中提出的预测校正方法通过结合数值SDE求解器(“预测器”)和迭代马尔可夫链蒙特卡罗(MCMC)方法(“校正器”)来解决反向SDE。在每个时间步，预测校正方法首先使用数值SDE求解器产生粗样本，然后使用基于分数的MCMC校正样本的边际分布的“校正器”。所得样本与逆时SDE的解轨迹具有相同的时间边际，即它们在所有时间步长的分布是相等的。实证结果表明，添加一个基于朗格万蒙特卡罗的校正器比使用一个没有校正器的额外预测器更有效[285]。Karras等人(2022)[141]进一步改进了[285]中的Langevin动态校正器，提出了添加和去除噪声的类似Langevin的“扰动”步骤，在CIFAR-10[161]和ImageNet-64[58]等数据集上实现了新的最先进的样本质量。
ODE solvers.
关于更快扩散采样器的大量工作是基于求解2.3节中介绍的概率流ODE (方程(19))。与SDE求解器相比，ode求解器的轨迹是确定的，因此不受随机波动的影响。这些确定性ODE解算器通常比随机解算器收敛得快得多，但代价是样本质量略差。
去噪扩散隐式模型(Diffusion Implicit Models, DDIM)[277]是加速扩散模型采样的最早工作之一。最初的动机是将原始的DDPM扩展到具有以下马尔可夫链的非马尔可夫情况
该公式将DDPM和DDIM封装为特例，其中DDPM对应于设置
，而DDIM对应于设置𝜎𝑡=0。DDIM学习马尔科夫链来逆转这种非马尔可夫扰动过程，当𝜎𝑡=0时，这是完全确定的。在[141,188,260,277]中观察到，DDIM采样过程相当于概率流ODE的特殊离散化方案。受单例数据集上ddim分析的启发，广义去噪扩散隐式模型(GDDIM)[372]提出了一种改进的Score网络的参数化，使得能够对更一般的扩散过程进行确定性采样，例如临界阻尼朗之万扩散(CLD)中的扩散过程[66]。PNDM[181]提出了一种沿着R-𝑁中特定流形生成样本的伪数值方法。它使用带有非线性转换部分的数值求解器来求解流形上的微分方程，然后生成样本，将ddim作为特例进行封装。
通过广泛的实验研究，Karras等人(2022)[141]表明，Heun的2𝑛𝑑阶数方法[8]在样本质量和采样速度之间提供了很好的权衡。高阶求解器的离散误差较小，代价是每时间步对学习到的分数函数进行一次额外的评估。Heun的方法产生的样本即使质量不比欧拉方法好，但抽样步骤更少。
扩散指数积分器采样器[371]和dpm求解器[188]利用概率流ODE的半线性结构来开发定制的ODE求解器，比通用的龙格-库塔方法更有效。具体来说，概率流ODE的线性部分可以解析计算，而非线性部分可以用类似于ODE求解器领域的指数积分器的技术来求解。这些方法包含DDIM作为一阶近似。然而，它们也允许更高阶的积分器，它可以在10到20次迭代中产生高质量的样本，远远少于扩散模型在没有加速采样的情况下通常需要的数百次迭代。
Learning-Based Sampling
基于学习的采样是扩散模型的另一种有效方法。通过使用部分步骤或训练采样器进行反向过程，该方法以样品质量的轻微下降为代价实现了更快的采样速度。与使用手工步骤的无学习方法不同，基于学习的抽样通常涉及通过优化某些学习目标来选择步骤。
Optimized Discretization.
对于预训练的扩散模型，Watson等人(2021)[313]提出了一种策略，通过选择最佳𝐾时间步长来寻找最优离散化方案，以最大化ddpm的训练目标。这种方法的关键是观察到DDPM目标可以分解为单个项的总和，使其非常适合动态规划。然而，众所周知，用于DDPM训练的变分下界与样本质量并不直接相关[294]。随后的一项工作，称为可微分扩散采样器搜索[312]，通过直接优化称为核初始距离(KID)[22]的样本质量通用度量来解决这个问题。在重参数化[156,252]和梯度重物化的帮助下，这种优化是可行的。Dockhorn等人(2022)[67]基于截断的Taylor方法，通过在一阶分数网络上训练一个额外的头部，推导出一个二阶解算器来加速合成。
Truncated Diffusion.
可以通过截断正向和反向扩散过程来提高采样速度[199,381]。关键思想是在几个步骤之后，尽早停止正向扩散过程，并开始使用非高斯分布进行反向去噪过程。通过从预训练的生成模型(如变分自编码器[156,252]或生成对抗网络[88])中扩散样本，可以有效地获得来自该分布的样本。
Knowledge Distillation.
使用知识蒸馏[190,205,260]的方法可以显著提高扩散模型的采样速度。具体来说，在渐进式蒸馏[260]中，作者建议将整个采样过程蒸馏成一个更快的采样器，只需要一半的步骤。通过将新的采样器参数化为一个深度神经网络，作者能够训练采样器来匹配DDIM采样过程的输入和输出。重复这个过程可以进一步减少采样步骤，尽管更少的步骤会导致样品质量下降。为了解决这一问题，作者提出了扩散模型的新参数化和目标函数的新加权方案。
Diffusion Models with Improved Likelihood
如2.1节所述，扩散模型的训练目标是对数似然的(负)变分下界(VLB)。然而，在许多情况下，这个界限可能并不紧密[154]，导致扩散模型的对数似然可能不是最优的。在本节中，我们调查了扩散模型的可能性最大化的最新工作。我们着重于三种类型的方法:噪声调度优化、反向方差学习和精确对数似然评估。
Noise Schedule Optimization
在经典的扩散模型公式中，正向过程中的噪声表是手工制作的，没有可训练的参数。通过与扩散模型的其他参数共同优化前向噪声调度，可以进一步最大化VLB，从而获得更高的对数似然值[154,214]。
iddpm[214]的工作表明，一定的余弦噪声调度可以提高对数似然。具体来说，余弦噪声时间表在他们的工作采取的形式
其中，𝑚是控制噪声尺度在𝑡= 0处的超参数。他们还提出了一种针对逆向过程方差的参数化方法，通过对数域（log domain）中 βt 和 1−αˉt 之间的插值来实现。
在变分扩散模型(Variational Diffusion Models, VDMs)中[154]，作者提出通过联合训练噪声调度和其他扩散模型参数来提高连续时间扩散模型的似然性，从而最大化VLB。他们使用单调神经网络𝜂(𝑡)对噪声调度进行参数化，并根据
构建前向扰动过程。此外，作者还证明了数据点x的负载均衡器可以简化为仅依赖于信噪比
的形式。其中，𝐿VLB变量可分解为
其中第一项和第二项可以直接优化，类似于训练变分自编码器。第三项可以进一步简化为:
式中，Rmax =𝑅(1)，Rmin =𝑅(𝑇)，x𝑣=¯gr𝑣x0 +𝑣𝑣<e:1>表示通过前向扰动过程将x0扩散至𝑡=𝑅−1()得到的有噪声数据点，≈x <e:1>表示通过扩散模型预测的无噪声数据点。因此，只要在Rmin和Rmax处具有相同的值，噪声调度就不会影响VLB，并且只会影响VLB的蒙特卡罗估计量的方差。
另一项研究[123,351]提出通过整合跨模态信息来修改扩散轨迹。具体来说，通过关系网络𝑟<s:2>(·)从任意条件输入的<s:2>(·)和原始样本𝑥0中提取跨模态信息，表示为𝑟<s:2>(·，𝑥0)。然后注入到正向过程中，作为一个额外的偏置来适应扩散轨迹:
其中𝑘𝑡是控制偏置项大小的非负标量。重要的是要注意，通过这种修改，前向过程不再是马尔可夫链。ContextDiff[351]引入了一个通用框架来联合学习跨模态关系网络𝑟<e:2>和扩散模型，并推导出这种改进的扩散过程的负载均衡和采样过程。
Reverse Variance Learning
经典的扩散模型公式假定逆马尔可夫链上的高斯转移核具有固定的方差参数。回想一下，我们在方程(5)中将反向核表示为𝑞es (x𝑡−1 | x𝑡)= N(Σ es (x𝑡，𝑡)，Σ es (x𝑡，𝑡))，但通常将反向方差𝑡es (x𝑡，𝑡)固定为i。许多方法提出也训练反向方差以进一步最大化VLB和对数似然值。
在iDDPM[214]中，Nichol和Dhariwal提出通过一种线性插值形式参数化反向方差，并使用混合目标训练它们来学习反向方差。这导致更高的对数似然和更快的采样，而不会损失样本质量。特别是，他们将方程(5)中的反向方差参数化为:
其中，时延时延为1 ~𝑡B 1−¯时延𝑡−1−¯时延𝑡·时延𝑡与时延为1−¯时延𝑡·时延𝑡与时延为1−¯时延𝑡·时延𝑡联合训练，最大限度地提高时延。这种简单的参数化避免了估计更复杂形式Σ (x𝑡，𝑡)的不稳定性，据报道可以提高似然值。
analysis - dpm[13]显示了一个显著的结果，即可以从预训练的分数函数中得到最优的反向方差，其解析形式如下:
因此，给定一个预训练分数模型，我们可以估计它的一阶和二阶矩，以获得最优的反向方差。将它们插入到VLB中可以导致更紧凑的VLB和更高的似然值。
Exact Likelihood Computation
在Score SDE[285]公式中，通过求解以下反向SDE生成样本，其中方程(18)中的∇x𝑡log𝑝(x𝑡，𝑡)替换为学习到的噪声条件分数模型s (x𝑡，𝑡):
在这里，我们使用𝑝sde()()()()()()表示通过求解上述SDE生成的样本的分布。也可以将得分模型代入方程(19)中的概率流ODE中生成数据，得到:
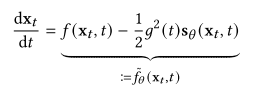
类似地，我们使用𝑝ode()()()()()来表示通过求解该ODE生成的样本的分布。神经ode[40]和连续归一化流的理论[92]表明，虽然计算成本较高，但可以准确地计算𝑝ode算法。对于𝑝sde系统，几个并行研究[119,187,279]表明存在一个有效可计算的变分下界，我们可以直接训练我们的扩散模型，使用修正的扩散损失来最大化𝑝sde系统。
具体而言，Song等人(2021)[279]通过特殊的加权函数(似然加权)证明了用于训练得分SDEs的目标隐式地最大化了𝑝sde对数据的期望值。结果表明
其中L(;𝑔(·)2)是方程(20)中的Score SDE目标，其中(𝑡)=𝑔(𝑡)2。由于D𝐾𝐿(𝑞0∥𝑝sde℃)=−E𝑞0 log(𝑝sde℃)+const，而D𝐾𝐿(𝑞𝑇∥∥)是常数，训练用L(℃;𝑔(·)2)相当于最小化- E𝑞0 log(𝑝sde temp)，即数据的预期负对数似然。此外，Song et al.(2021)和Huang et al.(2021)[119,279]给出了𝑝sde (x)的约束:
where L′(x) is defined by
方程(38)的第一部分让人想起隐式分数匹配[126]，整个边界可以用蒙特卡罗方法有效地估计。
由于概率流ODE是神经ODE或连续归一化流的特殊情况，我们可以使用这些领域中成熟的方法来准确地计算log𝑝ode ODE。具体来说，我们有
我们可以用数值ODE求解器和skill - hutchinson迹估计量来计算上述一维积分[125,274]。不幸的是，这个公式不能直接优化以最大化𝑝ode对数据的ODE，因为它需要为每个数据点x0调用昂贵的ODE求解器。为了降低使用上述公式直接最大化𝑝ode peer的成本，Song等人(2021)[279]提出最大化𝑝sde peer的变分下界作为最大化𝑝ode peer的代理，从而产生了一系列称为ScoreFlows的扩散模型。
Lu等人(2022)[187]进一步改进了ScoreFlows，提出不仅最小化普通分数匹配损失函数，而且最小化其高阶泛化。他们证明了log𝑝ode可以被一阶、二阶和三阶分数匹配错误限定。在此理论结果的基础上，作者进一步提出了有效的训练算法，以最大限度地减少高阶分数匹配损失，并报告了对数据的改进𝑝ode算法。
Diffusion Models for Data with Special Structures
虽然扩散模型在图像和音频等数据领域取得了巨大的成功，但它们并不一定能无缝地转化为其他模式。许多重要的数据域具有特殊的结构，扩散模型必须考虑到这些结构才能有效地发挥作用。例如，当模型依赖于仅在连续数据域中定义的分数函数时，或者当数据驻留在低维流形上时，可能会出现困难。为了应对这些挑战，必须以各种方式调整扩散模型。
Discrete Data
大多数扩散模型都是面向连续数据域的，因为ddpm中使用的高斯噪声扰动并不适合离散数据，SGMs和score sde所需的分数函数仅在连续数据域上定义。为了克服这一困难，一些研究[9,98,117,326]建立在Sohl-Dickstein等人(2015)[275]的基础上，以生成高维离散数据。具体来说，VQ-Diffusion[98]用离散数据空间上的随机游走或随机掩蔽操作取代高斯噪声。向前进程的最终转换内核采用的形式为
其中v(x)为单热列向量，Q𝑡为惰性随机漫步的迁移核。D3PM[9]通过构建具有吸收态核或离散高斯核的前向噪声过程来适应扩散模型中的离散数据。Campbell等人(2022)提出了离散扩散模型的第一个连续时间框架。利用连续时间马尔可夫链，他们能够推导出优于离散样本的有效采样器，同时提供样本分布与真实数据分布之间误差的理论分析。
具体分数匹配(Concrete Score Matching, CSM)[204]提出了对离散随机变量的分数函数的泛化。具体分数是由概率相对于输入方向变化的变化率来定义的，这可以看作是连续(Stein)分数的有限差分近似。具体分数可以有效地训练并应用于MCMC。
Liu等人(2023)[184]基于随机演算理论，提出了一种扩散模型框架，用于生成约束和结构化域上的数据，其中包括作为特例的离散数据。利用随机微积分中的一个基本定理，即Doob的h变换，可以通过在反向扩散过程中加入一个特殊的力项来约束数据在特定区域的分布。他们使用基于em的优化算法对力项进行参数化。利用Girsanov定理将损失函数转化为𝐿2损失。
Data with Invariant Structures
许多重要领域的数据具有不变结构。例如，图是排列不变量，点云是平移和旋转不变量。在扩散模型中，这些不变性经常被忽略，这可能导致次优性能。为了解决这个问题，一些研究[56,219]提出赋予扩散模型考虑数据不变性的能力。
Niu等人(2020)[219]首先用扩散模型解决了置换不变图生成问题。他们通过使用排列等变图神经网络[89,265,322](称为EDP-GNN)来参数化噪声条件评分模型来实现这一点。GDSS[134]通过提出连续时间图扩散过程进一步发展了这一思想。该过程通过随机微分方程(SDEs)系统对节点和边的联合分布进行建模，其中使用消息传递操作来保证排列不变性。
同样，Shi等人(2021)[267]和Xu等人(2022)[333]使扩散模型能够生成平移和旋转都不变的分子构象。例如，Xu等人(2022)[333]表明，从不变先验开始并以等变马尔可夫核进化的马尔可夫链可以诱导出不变的边际分布，这可以用于在分子构象生成中强制适当的数据不变性。形式上，设T是一个旋转或平移操作。假设
[333]证明了样本的分布保证对T不变，即𝑝0(x) =𝑝0(T(x))。因此，只要先验核和过渡核具有相同的不变性，就可以建立一个产生旋转和平移不变分子构象的扩散模型。
Data with Manifold Structures
具有流形结构的数据在机器学习中无处不在。正如流形假设[76]所假定的那样，自然数据通常存在于具有较低内在维数的流形上。此外，许多数据域具有众所周知的流形结构。例如，气候和地球数据自然位于球体上，因为这是我们星球的形状。许多工作都集中在开发流形数据的扩散模型上。我们根据流形是已知的还是习得的进行分类，并在下面介绍一些有代表性的作品。
Known Manifolds.
最近的研究已经将Score SDE公式扩展到各种已知的流形。这种适应与神经ode[40]和连续归一化流[92]推广到黎曼流形[186,201]相似。为了训练这些模型，研究人员还将分数匹配和分数函数适应于黎曼流形。
黎曼分数生成模型(RSGM)[56]可以容纳各种流形，包括球体和环体，只要它们满足温和的条件。RSGM证明了将扩散模型推广到紧黎曼流形是可能的。该模型还提供了流形上反向扩散的公式。从内禀的角度来看，RSGM近似黎曼流形上的采样过程使用测地线随机漫步。用广义去噪分数匹配目标对其进行训练。
相反，黎曼扩散模型(Riemannian Diffusion Model, RDM)[118]采用变分框架将连续时间扩散模型推广到黎曼流形。RDM使用对数似然的变分下界(VLB)作为其损失函数。RDM模型的作者已经证明，最大化这种负载均衡相当于最小化黎曼分数匹配损失。与RSGM不同，RDM采用外在观点，假设相关黎曼流形嵌入在高维欧几里德空间中。
Learned Manifolds.
根据流形假设[76]，大多数自然数据存在于内在维数显著降低的流形上。因此，由于数据维数较低，识别这些流形并直接在其上训练扩散模型是有利的。最近的许多工作都建立在这个想法之上，首先使用自动编码器将数据压缩成一个较低维的流形，然后在这个潜在空间中训练扩散模型。在这些情况下，流形由自编码器隐式定义，并通过重构损失学习。为了取得成功，设计一个允许自动编码器和扩散模型联合训练的损失函数是至关重要的。
基于潜在分数的生成模型(Latent Score- based Generative Model, LSGM)[299]试图通过将分数SDE扩散模型与变分自编码器(VAE)配对来解决联合训练问题[156,252]。在这种配置中，扩散模型负责学习先验分布。LSGM的作者提出了一个联合训练目标，该目标将VAE的证据下界与扩散模型的分数匹配目标合并。这将导致数据对数似然的新下界。通过将扩散模型置于潜在空间内，LSGM实现了比传统扩散模型更快的样本生成。此外，LSGM可以通过将离散数据转换为连续的潜在代码来管理离散数据。
潜伏扩散模型(Latent diffusion model, LDM)[255]不是联合训练自编码器和扩散模型，而是分别处理每个组件。首先，训练自编码器产生低维潜在空间。然后，训练扩散模型生成潜在代码。DALLE-2[243]采用了类似的策略，在CLIP图像嵌入空间上训练一个扩散模型，然后训练一个单独的解码器来基于CLIP图像嵌入创建图像。
扩散模型的结构导向对抗性训练(SADMs)[346]首次提出利用样本批内的结构信息。具体来说，sadm结合了一个对抗训练的结构鉴别器，以强制保存每个训练批内样本之间的流形结构。这种方法利用固有的数据流形来促进真实样本的生成，从而大大提高了以前的扩散模型在图像合成和跨域微调等任务中的能力。
Connections with Other Generative Models
在本节中，我们首先介绍其他五种重要的生成模型，并分析它们的优点和局限性。然后，我们介绍了扩散模型如何与它们联系起来，并说明了如何通过结合扩散模型来促进这些生成模型。表2总结了将扩散模型与其他生成模型相结合的算法，并在图中提供了示意图。
图3 将扩散模型与其他生成模型相结合的作品插图，例如:大型语言模型[347]中扩散模型由大型语言模型规划指导，VAE[255]中扩散模型应用于潜在空间，GAN[311]中将噪声注入鉴别器输入，归一化流[370]中将噪声注入到流的前向和后向过程中，自回归模型[116]，其中训练目标与扩散模型相似;EBM[83]，其中EBM序列通过扩散恢复似然学习。
Large Language Models and Connections with Diffusion Models
大型语言模型(Large Language Models, 大型语言模型)[1,7,27,129,348]深刻地影响了人工智能社区，并展示了先进的语言理解和推理能力。最近的研究开始将其令人印象深刻的推理能力扩展到总体生成规划的视觉生成任务。大型语言模型[35, 221, 348]和扩散模型[20,243,345,351]之间的协作可以显著提高文本-图像对齐以及生成图像的质量[177,295,375]。例如，RealCompo[375]利用大型语言模型通过生成基于大型语言模型的边界框布局的图像来增强扩散模型的组成生成。EditWorld[349]由一组大型语言模型和预训练扩散模型组成，生成包含大量具有世界知识的指令的图像编辑数据集[101]。VideoTetris[295]利用大型语言模型沿时间轴分解文本提示，引导视频生成更平滑、更合理的过渡。SemanticSDS[350]和Trans4D[366]扩展了大型语言模型的规划能力，以促进更复杂的3D和4D扩散生成。值得注意的是，RPG[347]利用多模态大型语言模型的视觉语言先验，从文本提示中推断出互补的空间布局，并在文本引导的图像生成和编辑过程中为扩散模型操纵对象组成。在合成场景中实现SOTA性能，并为后续研究提供指导。
Variational Autoencoders and Connections with Diffusion Models
变分自编码器[68,157,252]旨在学习编码器和解码器将输入数据映射到连续潜在空间中的值。在这些模型中，嵌入可以被解释为概率生成模型中的潜在变量，而概率解码器可以通过参数化似然函数来表示。此外，假设数据x是由一些未观察到的潜在变量z产生的，使用条件分布𝑝(x | z)，并使用𝑞 (z | x)来近似推断z。为了保证有效的推断，使用变分贝叶斯方法来最大化证据下界:
，假设参数化似然函数𝑝(x | z)和参数化后验逼近𝑞(z | x)可以逐点计算，且与参数可微，则ELBO可以通过梯度下降实现最大化。这个公式允许灵活选择编码器和解码器模型。通常，这些模型由指数族分布表示，其参数由多层神经网络生成。
DDPM可以被概念化为具有固定编码器的分层马尔可夫VAE。具体来说，DDPM的前向过程起到编码器的作用，该过程的结构为线性高斯模型(如方程(2)所示)。另一方面，DDPM的反向过程对应于解码器，它在多个解码步骤之间共享。解码器中的潜在变量都与样本数据的大小相同。
在连续时间环境下，Song等人(2021)[285]、Huang等人(2021)[119]和Kingma等人(2021)[154]证明，深度分层VAE的证据下界(Evidence Lower Bound, ELBO)可以近似实现分数匹配目标。因此，优化扩散模型可以看作是训练一个无限深度的分层vae——这一发现支持了Score SDE扩散模型可以被解释为分层vae的连续极限的普遍观点。
基于潜在分数的生成模型(Latent score - based Generative Model, LSGM)[299]通过说明ELBO可以被认为是潜在空间扩散背景下的一个专门的分数匹配目标，进一步推进了这一研究方向。虽然ELBO中的交叉熵项是难以处理的，但通过将基于分数的生成模型视为无限深度VAE，可以将其转化为可处理的分数匹配目标。
Generative Adversarial Networks and Connections with Diffusion Models
生成式对抗网络(GANs)[51,88,100]主要由两个模型组成:生成器𝐺和鉴别器𝐷。这两个模型通常由神经网络构建，但可以在任何形式的可微系统中实现，将输入数据从一个空间映射到另一个空间。gan的优化可以看作是一个值函数为(𝐺，𝐷)的最小-最大优化问题:
生成器𝐺旨在生成新的样例并隐式地对数据分布进行建模。鉴别器𝐷通常是一个二元分类器，用于以最大可能的精度从真实示例中识别生成的示例。优化过程在鞍点结束，鞍点产生关于生成器的最小值和关于鉴别器的最大值。也就是说，gan优化的目标是达到纳什均衡[250]。此时，可以认为生成器已经捕获了真实示例的准确分布。
gan的问题之一是训练过程中的不稳定性，这主要是由输入数据的分布与生成数据的分布不重叠引起的。一种解决方案是在鉴别器输入中注入噪声，以扩大发生器和鉴别器分布的支持度。Wang等人(2022)[311]利用柔性扩散模型，通过扩散模型确定的自适应噪声调度向鉴别器注入噪声。另一方面，GAN可以提高扩散模型的采样速度。Xiao等人(2021)[324]表明，缓慢的采样是由去噪步骤中的高斯假设引起的，只有在小步长时才合理。因此，每个去噪步骤都由条件GAN建模，允许更大的步长。为了确保扩散模型捕获数据分布中真实的流形结构，SADM[346]提倡在极小极大对策中对扩散生成器进行针对新结构鉴别器的对抗式训练，从而将真实流形结构与生成的流形结构区分开来。
Normalizing Flows and Connections with Diffusion Models
规范化流[63,251]是生成模型，生成可处理的分布来模拟高维数据[65,155]。归一化流可以将简单的概率分布转化为极其复杂的概率分布，可用于生成模型、强化学习、变分推理等领域。现有的归一化流是基于变量变换公式构建的[63,251]。归一化流的轨迹用微分方程表示。在离散时间设置中，在归一化流中从数据x到潜在z的映射是一系列双射的组合，其形式为:◦𝐹1。轨迹{x1, x2，…在规范化流中X操作满足:
for all 𝑖 ≤ 𝑁.
与连续设置类似，规范化流允许通过更改变量公式来检索精确的对数似然值。然而，在实践和理论背景下，双注入要求限制了复杂数据的建模[50,317]。一些作品试图放宽这种双射要求[65,317]。例如，DiffFlow[370]引入了一种生成建模算法，该算法结合了基于流模型和扩散模型的优点。因此，DiffFlow产生比归一化流更清晰的边界，并且与扩散概率模型相比，用更少的离散步骤学习更一般的分布。隐式非线性扩散模型(Implicit Nonlinear Diffusion Model, INDM)[150]对潜在扩散的预编码过程进行了优化，首先使用归一化流将原始数据编码到潜在空间中，然后在潜在空间中进行扩散。利用非线性扩散过程，INDM可以有效地提高似然度和采样速度。
为了扩大CNFs的训练规模，最近的工作提出了有效的无模拟方法[2,179,183]，通过参数化从噪声样本流向数据样本的向量场。Lipman等人(2022)[179]提出Flow Matching (FM)，通过在噪声分布和每个数据样本之间构建显式条件概率路径来训练cnf。Wang等人(2024)[307]深入分析了精流中精流的本质[183]，并将其扩展到精流扩散。并通过理论推导得出了一阶性质是整流扩散的基本训练目标，而不是直线性。Yang等人(2024)进一步提出了一致性流匹配[353]，这是一种新的FM方法，它显式地增强了速度场的自一致性。一致性流匹配[353]直接定义了从不同时间出发到同一端点的直线流，并对其速度值施加了约束:
其中U为[0,1−Δ𝑡]上的均匀分布，时延为正标量，Δ𝑡为时间间隔，是一个小的正标量。表示使用指数移动平均线(EMA)计算的过去值的运行平均值，其中，≥𝑡和≥𝑡+Δ𝑡遵循可以有效采样的预定义分布，例如，VP-SDE[111]或OT路径[179]。这样，一致性流匹配[353]通过以速度一致性为特征的新颖直流概念，创新性地将一致性模型和流匹配模型连接起来。
Autoregressive Models and Connections with Diffusion Models
自回归模型(ARMs)通过使用概率链式规则将数据的联合分布分解为条件分布的乘积来工作:
其中x<𝑡是𝑥1，𝑥2，…的简写。，≥𝑡−1[17,163]。深度学习的最新进展促进了各种数据模式的重大进展[34,207,264]，例如图像[45,302]，音频[140,301]和文本[18,27,95,203,211]。自回归模型(arm)通过使用单个神经网络提供生成能力。从这些模型中采样需要与数据维度相同数量的网络调用。虽然arm是有效的密度估计器，但采样是一个连续的、耗时的过程——特别是对于高维数据。
另一方面，自回归扩散模型(Autoregressive Diffusion Model, ARDM)[116]能够生成任意阶的数据，包括阶不可知的自回归模型和作为特殊情况的离散扩散模型[9,117,276]。与在arm等表征上使用因果掩蔽不同，ARDM是用一个反映扩散概率模型的有效目标来训练的。在测试阶段，ARDM能够并行地生成数据，使其应用程序能够执行一系列任意生成任务。
Mment等人(2021)[208]将随机平滑引入自回归生成模型中，以提高样本质量。通过将原始数据分布与平滑分布(例如，高斯或拉普拉斯核)卷积来平滑原始数据分布。通过自回归模型学习平滑后的数据分布，然后采用基于梯度的去噪方法或引入另一种条件自回归模型对学习到的分布进行去噪。通过适当地选择平滑程度，该方法可以在保持合理似然的前提下改善已有自回归模型的样本质量。
另一方面，自回归条件得分模型(AR-CSM)[210]提出了一种得分匹配方法来模拟自回归模型的条件分布。条件分布的得分函数，即∇𝑥𝑡𝑝(𝑥𝑡|x<；𝑡)不需要正规化，因此可以在模型中使用更灵活和更先进的神经网络。此外，即使原始数据的维度可能很高，也可以有效地估计单变量条件得分函数。对于推理，AR-CSM使用朗之万动力学，它只需要得分函数来从密度中采样。
Energy-based Models and Connections with Diffusion Models
基于能量的模型(EBMs)[36、59、70、77、81、82、90、93、94、153、162、165、213、218、238、253、325、378]可以看作是判别器[94、130、164、168]的一种生成版本，同时可以从未标记的输入数据中学习。设x ~𝑝data (x)表示训练样例，𝑝(x)表示旨在近似𝑝data (x)的概率密度函数。基于能量的模型定义为:
其中𝑍
是配分函数，对于高维x是解析难以处理的。对于图像，𝑓(x)由具有标量输出的卷积神经网络参数化。Salimans等人(2021)[261]比较了约束分数模型和基于能量的模型来建模数据分布的分数，发现在使用可比较的模型结构时，约束分数模型，即基于能量的模型，可以像无约束模型一样执行得很好。
尽管ebm具有许多理想的特性，但是对高维数据建模仍然存在两个挑战。首先，通过最大化似然来学习ebm需要MCMC方法从模型中生成样本，这在计算上是非常昂贵的。其次，如文献[217]所示，用非收敛的MCMC学习到的能量势是不稳定的，这意味着来自长期马尔可夫链的样本可能与观测到的样本存在显著差异，因此很难评估学习到的能量势。在最近的一项研究中，Gao等人(2021)[83]提出了一种扩散恢复似然方法，可以在扩散模型的反向过程中从一系列EBMs中跟踪学习样本。每个EBM都用恢复似然进行训练，其目的是在给定更高噪声水平下的噪声版本的情况下，使数据在一定噪声水平下的条件概率最大化。EBMs使恢复可能性最大化，因为它比边际可能性更容易处理，因为从条件分布中抽样比从边际分布中抽样容易得多。
Applications of Diffusion Models
由于其灵活性和强度，扩散模型最近被用于解决各种具有挑战性的现实世界任务。我们根据任务将这些应用分为六个不同的类别:计算机视觉、自然语言处理、时间数据建模、多模态学习、鲁棒的学习和跨学科应用。对于每个类别，我们都简要介绍了任务，然后详细解释了如何应用扩散模型来提高性能。表3总结了使用扩散模型的各种应用程序。
Unconditional and Conditional Diffusion Models
在介绍扩散模型的应用之前，我们先说明扩散模型的两种基本应用范例，即无条件扩散模型和条件扩散模型。作为一种生成模型，扩散模型的历史与VAE、GAN、流动模型等生成模型非常相似。它们都首先发展了无条件代，然后紧随其后的是条件代。无条件生成通常用于探索生成模型性能的上限，而条件生成更多的是应用级内容，因为它可以使我们根据我们的意图控制生成结果。扩散模型除了具有良好的生成质量和样本多样性外，在可控性方面尤其优越。无条件扩散模型的主要算法已经在第2节到第5节中进行了很好的讨论，在下一部分中，我们将主要讨论条件扩散模型如何应用于不同形式条件下的不同应用，并选择一些典型的场景进行演示。
Conditioning Mechanisms in Diffusion Models.
利用不同形式的条件来引导扩散模型的生成方向被广泛使用，如标签、分类器、文本、图像、语义图、图形等。然而，有些条件是结构性的、复杂的，因此对这些条件的条件设置方法值得探讨。主要有四种调节机制，包括串联机制、梯度机制、交叉注意机制和自适应层归一化机制。串联是指扩散模型在扩散过程中将信息制导与中间去噪目标进行串联，如标签嵌入和语义特征映射。基于梯度的机制将任务相关梯度集成到扩散采样过程中以实现可控生成。例如，在图像生成中，可以在有噪声的图像上训练辅助分类器，然后使用梯度将扩散采样过程引导到任意类标号。交叉注意在制导目标和扩散目标之间进行注意信息的传递，在去噪网络中通常采用分层方式进行。adaLN机制遵循gan[142]中自适应归一化层的广泛使用[231]，可扩展扩散模型[229]探索用自适应层归一化取代基于变压器的扩散骨干中的标准层规范层。它不是直接学习维度尺度和移位参数，而是从时间嵌入和条件的总和中回归它们。
Diffusion with DPO/RLHF.
基于大型语言模型(大型语言模型)中人类反馈强化学习(RLHF)的成功[11,224]，扩散模型中的许多方法都试图使用类似的方法进行模型对齐[75,167]。有些方法使用预训练的奖励模型或训练新的奖励模型来指导生成过程。例如，ImageReward[330]手动注释了人类偏好图像的大型数据集，并训练了一个奖励模型来评估图像与人类偏好之间的一致性。一些方法绕过奖励模型的训练，直接在人类偏好数据集上微调扩散模型[339]。diffusion -DPO[306]重新表述了直接偏好优化(DPO)，以解释扩散模型的可能性概念，利用证据下界推导出一个可微目标。最近，Zhang等人(2024)提出了IterComp[376]，迭代地将基础扩散模型与由六个强大的开源扩散模型组成的模型库中的组合感知模型偏好对齐，有效地提高了基础模型在条件扩散生成方面的性能。如图所示，IterComp[376]在达到最佳推理效率的同时，优于其他三种条件扩散方法。.
Condition Diffusion on Labels and Classifiers.
在标签的引导下调节扩散过程是一种直接向生成的样品中添加所需性质的方法。然而，当标签有限时，很难使扩散模型充分捕捉数据的整个分布。SGGM[352]提出了一种基于自生成的分层标签集的自引导扩散过程条件调节，而You等人(2023)[359]通过双伪训练证明了大规模扩散模型和半监督学习器在少量标签下相互受益。Dhariwal和Nichol提出了分类器指导，通过使用额外训练的分类器来提高扩散模型的样本质量。Ho和Salimans[113]共同训练了一个条件和无条件扩散模型，并发现可以将得到的条件和无条件分数结合起来，获得样本质量和多样性之间的权衡，类似于使用分类器引导得到的结果。
Condition Diffusion on Texts, Images, and Semantic Maps.
近年来的研究开始在文本、图像、语义图等更多语义的指导下调节扩散过程，以更好地表达样本中丰富的语义。DiffuSeq[86]在文本上设置条件，并提出了一个序列到序列的扩散框架，该框架有助于完成四个NLP任务。SDEdit[206]在样式图像上设置条件以进行图像到图像的翻译，而LDM[255]通过灵活的潜在扩散将这些语义条件统一起来。请注意，如果条件和扩散目标具有不同的模式，预对准[243,342]是加强引导扩散的实用方法。unCLIP[243]和ConPreDiff[345]在文本到图像的生成中利用CLIP的潜力，使图像和文本之间的语义对齐。RPG[347]在互补的矩形和轮廓区域上设置条件，以实现合成文本到图像的生成和复杂的文本引导图像编辑。ContextDiff[351]提出了一种通用的前向后一致扩散模型，用于更好地调节各种输入模式。
Condition Diffusion on Graphs.
图结构数据通常在节点之间表现出复杂的关系，因此扩散模型很难对图进行条件调节。SGDiff[342]提出了第一个专门为场景图到图像生成设计的扩散模型，该模型采用了一种新颖的掩模对比预训练。这种掩蔽预训练范式是通用的，可以扩展到任何跨模态扩散架构，用于粗粒度和细粒度指导。其他图条件扩散模型主要用于图的生成。Graphusion[343]利用图数据集的潜在聚类来生成与数据分布高度一致的新2D图。BindDM[121]、IPDiff[124]和IRDiff[122]提出在三维蛋白图上条件，生成具有等变扩散的三维分子。
Computer Vision
Image Super Resolution, Inpainting, Restoration, Translation, and Editing.
生成模型已被用于处理各种图像恢复任务，包括超分辨率、上漆和翻译[16,58,74,128,171,225,244,379]。图像超分辨率旨在从低分辨率输入恢复高分辨率图像，而图像修复则围绕重建图像中缺失或损坏的区域展开。
有几种方法利用扩散模型来完成这些任务。例如，通过重复细化的超分辨率(SR3)[259]使用DDPM来实现条件图像生成。SR3通过随机迭代去噪过程实现超分辨率。级联扩散模型(cascading Diffusion Model, CDM)[112]由多个扩散模型按顺序组成，每个模型生成的图像分辨率不断增加。SR3和CDM都直接将扩散过程应用于输入图像，这导致了更大的评估步骤。为了允许在有限的计算资源下训练扩散模型，一些方法[255,299]使用预训练的自编码器将扩散过程转移到潜在空间。潜在扩散模型(Latent Diffusion Model, LDM)[255]在不牺牲质量的情况下简化了扩散模型去噪的训练和采样过程。
对于绘制任务，RePaint[189]具有增强的去噪策略，该策略使用重采样迭代来更好地调节图像。ConPreDiff[345]提出了一种基于上下文预测的通用扩散模型，以持续改进无条件/条件图像生成和图像绘制(见图)。同时，Palette[257]采用条件扩散模型为四种图像生成任务创建了统一的框架:着色，绘画，裁剪和JPEG恢复。图像翻译的重点是合成具有特定所需样式的图像[128]。SDEdit[206]在提高保真度之前使用了随机微分方程(SDE)。具体来说，它首先向输入图像添加噪声，然后通过SDE对图像进行去噪。去噪扩散恢复模型(Denoising Diffusion Restoration Models, DDRM)[143]利用预训练的去噪扩散生成模型来解决线性逆问题，并展示了DDRM在不同测量噪声量下的超分辨率、去模糊、上色和着色等多个图像数据集上的通用性。有关更多文本到图像扩散模型，请参阅第7.4.1节。
Semantic Segmentation.
语义分割的目的是根据已建立的对象类别标记每个图像像素。生成式预训练可以提高语义分割模型的标签利用率，最近的研究表明，通过DDPM学习的表示包含对分割任务有用的高级语义信息[15,91]。利用这些学习表征的少量样本学习方法优于VDVAE b[44]和ALAE[232]等替代方法。同样，解码器去噪预训练(Decoder Denoising Pretraining, DDeP)[25]将扩散模型与去噪自动编码器集成在一起[305]，并在标签高效语义分割方面取得了令人满意的结果。ODISE[329]探索了开放词汇分割任务的扩散模型，并提出了一种新的隐式标题器来为图像生成标题，以便更好地利用预训练的大规模文本到图像扩散模型。
Video Generation.
由于视频帧的复杂性和时空连续性，在深度学习时代生成高质量视频仍然是一个挑战[341,362]。最近的研究转向扩散模型来提高生成视频的质量[114]。例如，柔性扩散模型(FDM)[107]使用生成模型，允许在给定任何其他子集的情况下对视频帧的任意子集进行采样。FDM还包括为此目的设计的专门架构。此外，残差视频扩散(RVD)模型[355]采用自回归的端到端优化视频扩散模型。它通过修正确定性的下一帧预测来生成未来帧，使用通过逆扩散过程产生的随机残差。有关更多文本到视频扩散模型，请参阅第7.4.5节。
Generating Data from Diffusion Models.
从生成模型合成数据集可以有效地推进分类等各种任务[12,309,385]。最近的工作已经开始利用扩散模型来实现视觉任务的这一目标。如Trabucco等人[297]采用扩散模型对少拍图像分类进行有效的数据增强。DistDiff[385]提出了一个具有分布感知扩散模型的无训练数据扩展框架。该方法通过构建层次原型来逼近真实数据分布，并利用层次能量引导优化生成过程中的潜在数据点。InstructPix2Pix[26]利用两个大型预训练模型(即GPT-3和Stable Diffusion)生成输入-目标-指令三重样例的大型数据集，并在数据集上训练一个指令跟随的图像编辑模型。为了使图像编辑能够反映来自真实物理世界和虚拟媒体的具有挑战性的世界知识和动态，EditWorld[349]引入了一个名为世界指示图像编辑的新任务，如图所示的数据示例。EditWorld提出了一种创新的合成框架，其中包含一组预训练的大型语言模型和扩散模型，如图8所示，用于合成一个用于指令跟随图像编辑的世界指导训练数据集。
Point Cloud Completion and Generation.
点云是捕捉真实世界物体的一种关键的3D表现形式。然而，扫描往往产生不完整的点云，由于部分观测或自遮挡。最近的研究已经应用扩散模型来解决这一挑战，使用它们来推断缺失的部分，以重建完整的形状。这项工作对许多下游任务有启示，如3D重建、增强现实和场景理解[194,198,367]。
Luo等人2021[193]采用了将点云视为热力学系统中的粒子的方法，使用热浴来促进从原始分布向噪声分布的扩散。同时，点体素扩散(Point-Voxel Diffusion, PVD)模型[384]将去噪扩散模型与三维形状的点体素表示结合起来。点扩散-细化(PDR)模型[198]使用条件DDPM从部分观测生成粗补全;它还建立了生成的点云和真实值之间的逐点映射。
Anomaly Detection.
异常检测是机器学习[266,380]和计算机视觉[337]中一个关键且具有挑战性的问题。生成模型已被证明具有异常检测的强大机制[84,105,323]，可以为正常或健康的参考数据建模。AnoDDPM[323]利用DDPM破坏输入图像并重建图像的健康近似值。这些方法可能比基于对抗性训练的替代方法表现更好，因为它们可以通过有效的采样和稳定的训练方案更好地对较小的数据集进行建模。DDPM- cd[84]通过DDPM将大量无监督遥感图像纳入训练过程。利用预训练的DDPM和扩散模型解码器的多尺度表示来检测遥感图像的变化。
Natural Language Generation
自然语言处理旨在理解、建模和管理来自不同来源(如文本或音频)的人类语言。文本生成已经成为自然语言处理中最关键和最具挑战性的任务之一[127,172,173]。它的目标是在给定输入数据(例如，序列和关键字)或随机噪声的情况下，用人类语言编写可信且可读的文本。许多基于扩散模型的文本生成方法已经被开发出来。离散去噪扩散概率模型(D3PM)[9]为字符级文本生成引入了类似扩散的生成模型[38]。它通过超越具有均匀转移概率的腐败过程，推广了多项扩散模型[117]。大型自回归语言模型(LMs)能够生成高质量的文本[27,46,242,373]。为了在实际应用程序中可靠地部署这些lm，通常期望文本生成过程是可控的。这意味着我们需要生成能够满足所需需求的文本(例如，主题、句法结构)。在不重新训练的情况下控制语言模型的行为是文本生成中的一个主要和重要问题[54,147]。模拟比特[42]产生模拟比特来表示离散变量，并通过自调节和非对称时间间隔进一步提高采样质量。
尽管最近的方法在控制简单句子属性(如情感)方面取得了显著的成功[160,338]，但在复杂的、细粒度的控制(如句法结构)方面进展甚微。为了处理更复杂的控制，diffusion - lm[175]提出了一种基于连续扩散的新语言模型。DiffusionLM从一系列高斯噪声向量开始，并逐渐将它们降噪为与单词对应的向量。逐步去噪步骤有助于产生分层连续的潜在表示。这种分层和连续的潜在变量可以使简单的、基于梯度的方法来完成复杂的控制。
同样，DiffuSeq[86]也在潜在空间中进行扩散过程，并提出了一种新的条件扩散模型来完成更具挑战性的文本到文本生成任务。Ssd-LM[106]在自然词汇空间上进行扩散，而不是在学习的潜在空间上进行扩散，从而允许模型在不适应现有分类器的情况下结合分类器引导和模块化控制。CDCD[61]提出用时间和输入空间连续的扩散模型对分类数据(包括文本)建模，并设计了分数插值技术进行优化。
Multi-Modal Generation
Text-to-Image Generation.
由于潜在应用的数量众多，视觉语言模型最近引起了很多关注[240]。文本到图像生成是从描述性文本生成相应图像的任务[69,146,300]。混合扩散[10]同时利用预训练的DDPM[60]和CLIP[240]模型，提出了一种基于区域的通用图像编辑解决方案，使用自然语言引导，适用于真实和多样化的图像。另一方面，unCLIP (DALLE-2)[243]提出了一种两阶段的方法，一种先验模型可以生成以文本标题为条件的基于clip的图像嵌入，另一种基于扩散的解码器可以生成以图像嵌入为条件的图像。最近，Imagen[258]提出了一种文本到图像的扩散模型和性能评估的综合基准。研究表明，Imagen在VQ-GAN+CLIP[52]、潜在扩散模型[188]和dall - e2[243]等最先进的方法中表现良好。受引导扩散模型[60,113]生成逼真样本的能力和文本到图像模型处理自由形式提示的能力的启发，GLIDE[215]将引导扩散应用于文本条件图像合成的应用。VQ-Diffusion[98]提出了一种用于文本到图像生成的矢量量化扩散模型，该模型消除了单向偏差，避免了累积预测误差。通用扩散[334]提出了第一个统一的多流多模态扩散框架，该框架支持图像到文本、图像变化、文本到图像和文本变化，并可以进一步扩展到其他应用，如语义风格解纠缠、图像-文本双引导生成、潜在的图像-文本-图像编辑、还有更多。继Versatile Diffusion之后，UniDiffuser[14]提出了一种基于Transformer的统一扩散模型框架，可以适应多模态数据分布，同时处理文本到图像、图像到文本以及图像-文本联合生成任务。ConPreDiff[345]首次将上下文预测整合到文本到图像扩散模型中，在不增加推理成本的情况下显著提高了生成性能。ContextDiff[351]通过将包含相互作用和对齐的跨模态上下文纳入正向和反向过程，提出了一般情境化扩散模型。图10所示为这些模型之间的定性比较。
扩散模型研究的一个有趣的新方向是利用预训练的文本到图像扩散模型对合成结果进行更复杂或更细粒度的控制。DreamBooth[256]提出了第一个解决主题驱动生成的新挑战问题的技术，允许用户从一些随意捕获的主题图像中重新定义主题，修改其属性，原始艺术再现等等。与那些以文本提示为条件的图像扩散模型不同，ControlNet[368]试图控制预训练的大型扩散模型来支持额外的语义图，如边缘图、分割图、关键点、形状法线、深度等。但是，大多数方法在处理涉及具有多个属性和关系的多个对象的复杂文本提示时经常面临挑战。为此，RPG[347]提出了一种全新的无需训练的文本到图像的生成/编辑框架，利用多模态大型语言模型[377]强大的思维链推理能力来增强文本到图像扩散模型的组合性。这个新的RPG框架将文本引导的图像生成(如图所示)和图像编辑(如图12所示)任务以闭环方式统一起来。值得注意的是，如图所示，RPG优于所有SOTA方法，如SDXL[233]和DALL-E 3[20]，证明了它的优越性。此外，RPG框架是用户友好的，可以推广到不同的mlm体系结构和扩散骨干(例如，ControlNet)。
Scene Graph-to-Image Generation.
尽管文本到图像的生成模型已经从自然语言描述中取得了令人兴奋的进展，但它们很难忠实地再现具有许多对象和关系的复杂句子。从场景图(SGs)生成图像是生成模型的一项重要且具有挑战性的任务[135]。传统方法[109,135,176]主要是从SGs中预测类图像布局，然后根据布局生成图像。然而，这种中间表示在SGs中会失去一些语义，并且最近的扩散模型[255]也无法解决这一限制。SGDiff[342]提出了第一个专门用于从场景图生成图像的扩散模型(图)，并学习了一个连续的SG嵌入来调节潜在扩散模型，该模型通过设计的屏蔽对比预训练在SGs和图像之间进行了全局和局部语义对齐。与非扩散和扩散方法相比，SGDiff可以生成更好地表达SGs中密集和复杂关系的图像。然而，高质量的配对图像数据集是稀缺和小规模的，如何利用大规模的文本图像数据集来增强训练或提供更好的初始化的语义扩散仍然是一个悬而未决的问题。
Text-to-3D Generation.
3D内容生成[139,178,234,331]在广泛的应用中有很高的需求，包括游戏、娱乐和机器人模拟。用自然语言增强3D内容生成对新手和有经验的美术师都有很大帮助。DreamFusion[234]采用预训练的2D文本到图像扩散模型进行文本到3d合成。它利用概率密度蒸馏损失优化随机初始化的3D模型(神经辐射场，或NeRF)，该模型利用2D扩散模型作为优化参数图像生成器的先验。为了实现NeRF的快速高分辨率优化，Magic3D[178]提出了一种基于级联低分辨率图像扩散先验和高分辨率潜在扩散先验的两阶段扩散框架。为了实现高保真的3D创建，Make-It-3D[290]通过结合正面视图参考图像的约束和新视图的扩散先验来优化神经辐射场。将粗糙模型增强为有纹理的点云，并使用参考图像的扩散先验和高质量纹理来增加真实感。prolificdreaming[310]提出了变分评分蒸馏(VSD)，基于文本提示作为随机变量来优化3D场景的分布，以KL散度为度量，从所有角度将渲染图像的分布与预训练的2D扩散模型紧密结合。ipdream[365]进一步提出了一种新的3D对象合成框架，使用户能够毫不费力地创建可控的高质量3D对象。它擅长于合成高质量的3D对象，可以极大地与提供的复杂图像提示对齐。
合成三维数据分布建模是生成模型的基础和关键任务。目前的前馈方法[27,271]主要能够生成单个对象，由于训练数据有限，在创建包含多个对象的更复杂场景时面临挑战。最近，人们提出了一系列可学习的布局组合方法[43,73,80,104,303]。这些方法结合了多个物体的特殊亮度场，然后从外部反馈中优化亮度场的位置。例如，Epstein等人[73]提出仅基于预训练的大型文本到图像模型的知识来学习合理布局的分布。Vilesov等人[303]介绍了一种基于蒙特卡罗采样和物理约束的优化方法。然而，这些形式的布局指导相对粗糙，对于细粒度的控制来说表达力不够。Yang等人(2024)[350]通过结合语义嵌入来解决这个问题，语义嵌入确保了视图一致性，并将对象明显地区分为SDS过程(即SemanticSDS[350])，这对于优化3D场景来说是灵活和富有表现力的。如图所示，与现有方法相比，SemanticSDS[350]在合成文本到3d生成方面可以达到更高的精度和质量。
Text-to-Motion Generation.
人体运动生成是计算机动画中的一项基本任务，其应用范围从游戏到机器人[369]。生成运动通常是由关节旋转和位置表示的一系列人体姿势。运动扩散模型(Motion Diffusion Model, MDM)[292]采用了一种无分类器的基于扩散的人体运动生成模型，该模型基于变压器，结合了运动生成文献的见解，并对运动位置和速度的几何损失模型进行了正则化。FLAME[151]涉及基于变压器的扩散，以更好地处理运动数据，管理可变长度的运动，并很好地处理自由格式的文本。值得注意的是，它可以编辑运动的部分，包括帧和关节，而无需任何微调。
Text-to-Video Generation.
近年来基于文本到图像扩散的生成技术取得了巨大进展，这推动了文本到视频生成技术的发展[110,273,318]。Make-A-Video[273]提出通过时空分解扩散模型将基于扩散的文本到图像模型扩展到文本到视频。它利用联合文本-图像，绕过对配对文本-视频数据的需求，并进一步提出了高分辨率、高帧率文本-视频生成的超分辨率策略。Imagen Video[110]通过设计级联视频扩散模型生成高清晰度视频，并将一些在文本到图像设置中工作良好的发现转移到视频生成中，包括冻结T5文本编码器和无分类器引导。Tune-A-Video[318]引入了用于文本到视频生成的一次视频调优，消除了使用大规模视频数据集进行训练的负担。采用有效的注意调谐和结构反转，显著提高了时间一致性。Text2Video-Zero[148]使用预训练的文本到图像扩散模型实现零样本学习文本到视频合成，通过潜在代码中的运动动力学和跨帧注意确保时间一致性。它的目标是实现经济实惠的文本引导视频生成和编辑，而无需额外的微调。FateZero[237]是第一个使用预训练的文本到图像扩散模型进行时间一致的零样本学习文本到视频编辑的框架。它融合了DDIM反演和生成过程中的注意图，最大限度地保持了编辑过程中运动和结构的一致性。ContextDiff[351]将文本条件与视频样本相互作用的跨模态上下文信息整合到正向和反向过程中，形成了文本到视频生成的前后向一致的视频扩散模型。
大多数文本到视频的扩散模型是在固定大小的视频数据集上训练的，因此通常仅限于生成相对较少的帧数，当生成较长的视频时，导致质量显著下降。一些进步[108,295,388]试图通过各种策略克服这一限制。Vlogger[388]采用屏蔽扩散模型进行条件帧输入，促进更长的视频生成，StreamingT2V[108]利用类似controlnet的条件调节机制实现自动回归视频生成。最近的VideoTetris[295]引入了一种时空合成扩散方法，用于处理具有多个对象的场景，并遵循渐进式复杂提示(即合成文本到视频生成)。此外，VideoTetris还开发了一种新的视频数据预处理方法和一致性正则化方法——参考帧注意(Reference Frame Attention)，通过增强运动动力学和提示语义来改进自回归长视频生成。图中的定性比较表明，VideoTetris不仅可以生成高质量的合成视频，还可以生成高质量的长视频，这些视频在保持最佳一致性的同时与合成提示保持一致。
Text-to-Audio Generation.
文本到音频的生成是将正常语言文本转换为语音输出的任务[170,320]。Grad-TTS[235]提出了一种新的文本到语音模型，该模型具有基于分数的解码器和扩散模型。它逐渐变换编码器预测的噪声，并通过单调对齐搜索(Monotonic Alignment Search)的方法进一步与输入的文本对齐[239]。Grad-TTS2[152]以自适应方式改进了Grad-TTS。Diffsound[336]提出了一种基于离散扩散模型[9,275]的非自回归解码器，它在每一步中预测所有的梅尔谱图标记，然后在接下来的步骤中对预测的标记进行细化。EdiTTS[288]利用基于分数的文本到语音模型来改进粗略修改的mel谱图。ProDiff[120]不是估计数据密度的梯度，而是通过直接预测干净数据来参数化去噪扩散模型。
Temporal Data Modeling
Time Series Imputation.
时间序列数据广泛用于许多重要的现实应用[72,223,341,374]。然而，由于机械或人为误差等多种原因，时间序列通常会包含缺失值[272,289,356]。近年来，归算方法主要有确定性归算[32,37,197]和概率归算[78]，其中包括基于扩散的方法。基于条件分数的扩散模型(Conditional Score-based Diffusion models for Imputation, CSDI)[291]提出了一种利用基于分数的扩散模型的新型时间序列Imputation方法。具体来说，为了挖掘时间数据之间的相关性，采用自监督训练的形式来优化扩散模型。在一些实际数据集上的应用显示了它比以往方法的优越性。控制随机微分方程(CSDE)[228]提出了一种新的概率框架，用神经控制随机微分方程来建模随机动力学。结构化状态空间扩散(SSSD)[3]集成了条件扩散模型和结构化状态空间模型[97]，以特别捕获时间序列中的长期依赖关系。它在时间序列imputation和预测任务中都表现良好。
Time Series Forecasting.
时间序列预测。时间序列预测是在一段时间内预测或预测未来价值的任务。神经网络方法最近被广泛用于解决单变量点预测方法[222]或单变量概率方法[262]的预测问题。在多变量设置中，我们也有点预测方法[174]和概率方法，它们使用高斯copulas[263]、gan[358]或归一化流[249]来显式地建模数据分布。TimeGrad[248]提出了一种用于预测多变量概率时间序列的自回归模型，该模型通过估计其梯度从每个时间步的数据分布中采样。它采用扩散概率模型，该模型与分数匹配和基于能量的方法密切相关。具体来说，它通过优化数据似然的变分界来学习梯度，并在推理期间使用朗格万抽样[280]通过马尔可夫链将白噪声转换为感兴趣分布的样本。为了处理复杂的时间序列预测，如图所示，Liu等人(2024)首次引入了检索-增强时间序列扩散(RATD)[180]，允许更大程度地利用数据集，并在去噪过程中提供有意义的指导。
Waveform Signal Processing.
在电子学、声学和一些相关领域中，信号的波形由其图形的形状表示为时间的函数，与时间和幅度尺度无关。WaveGrad[39]引入了一种用于波形生成的条件模型，用于估计数据密度的梯度。它接收高斯白噪声信号作为输入，并使用基于梯度的采样器对信号进行迭代细化。WaveGrad自然地通过调整改进步骤的数量来交换样本质量的推理速度，并在非自回归和自回归模型之间建立关于音频质量的连接。DiffWave[159]提出了一种通用且有效的扩散概率模型，用于条件或无条件波形的生成。该模型是非自回归的，并通过优化数据似然的变分界的变体来有效地训练。此外，在不同的波形生成任务中，如类条件生成和无条件生成，它可以产生高保真音频。
Robust Learning
鲁棒的学习是一类防御方法，它可以帮助学习网络，使其对对抗性扰动或噪声具有鲁棒的[23,216,232,308,319,357]。虽然对抗性训练[200]被视为图像分类器对抗对抗性攻击的标准防御方法，但对抗性净化作为一种替代防御方法已经显示出显著的性能[357]，它使用独立的净化模型将被攻击的图像净化成干净的图像。给定一个对抗性示例，DiffPure[216]在正向扩散过程中使用少量噪声对其进行扩散，然后通过反向生成过程恢复干净的图像。自适应去噪净化(Adaptive Denoising Purification, ADP)[357]表明，经过去噪分数匹配[304]训练的EBM只需几步就能有效地净化被攻击的图像。在此基础上提出了一种有效的随机净化方案，即在净化前向图像中注入随机噪声。投影梯度下降(PGD)[23]提出了一种新的基于随机扩散的预处理鲁棒化方法，旨在成为一种与模型无关的对抗防御，并产生高质量的去噪结果。此外，一些研究提出将引导扩散过程应用于高级对抗净化[308,319]。
Interdisciplinary Applications.
Drug Design and Life Science.
图神经网络[102,322,344,383]和相应的表示学习[103]技术在许多领域取得了巨大的成功[21,293,321,332,340,387]，包括在各种任务中建模分子/蛋白质，从性质预测[71,85]到分子/蛋白质生成[131,138,195,268]。分子通常用节点边图来表示。一方面，最近的研究提出针对具有生物医学或物理见解的分子/蛋白质进行GNN/transformer预训练[192,382]，并取得了显著的效果[182,364]。另一方面，越来越多的研究开始利用基于图的扩散模型来增强分子或蛋白质的生成。扭转扩散[133]提出了一种新的扩散框架，通过超空间上的扩散过程和外在到内在的评分模型对扭转角空间进行操作。GeoDiff[333]证明了用等变马尔可夫核进化的马尔可夫链可以产生不变分布，并进一步为马尔可夫核设计块以保持理想的等变性。也有其他研究将等方差性纳入三维分子生成[115]和蛋白质生成[5,19]。ConfGF[267]受模拟分子动力学的经典力场方法的启发，直接估计分子构象生成中原子坐标对数密度的梯度场。
最近，在给定靶标蛋白的情况下，通过扩散模型开始促进能够与靶标紧密结合的3D药物小分子的设计[99,122,124]。IPDiff[124]提出了一种新的基于结构的药物设计(SBDD)的3D分子扩散模型。如图所示，口袋配体相互作用在正向和反向过程中都被明确地考虑，并提出了先验条件反射和先验转移机制。值得注意的是，IPDiff在结合相关指标和分子特性方面击败了所有先前基于扩散和自回归的生成模型。BindDM[121]提出了一种用于SBDD任务的分层复合物-亚复合物扩散模型，该模型包含用于3D分子扩散生成的基本结合自适应亚复合物。IRDiff[124]针对SBDD任务提出了一种基于交互的检索增强3D分子扩散模型IRDiff。如图所示，该模型利用信息丰富的外部靶标感知参考来指导三维分子生成，设计了两种新的增强机制，即检索增强和自我增强，以结合必需的蛋白质-分子结合结构来进行靶标感知分子生成。
也有研究使用扩散模型来产生蛋白质，如DiffAb。DiffAb[196]首次提出了一种基于扩散的3D抗体设计框架，该框架对决定抗体互补性的互补决定区域(cdr)的序列和结构进行建模。实验表明，DiffAb可用于多种抗体设计任务，如联合生成序列结构、设计固定框架的cdr、优化抗体等。SMCDiff[298]提出首先通过E(3)-等变图神经网络学习不同和更长的蛋白质骨干结构的分布，然后根据给定的基序从该分布中有效地采样支架。生成结果表明，所设计的主干与alphafold2预测的结构很好地对齐。
Material Design.
固态材料是许多关键技术的重要基础。晶体扩散变分自编码器(Crystal Diffusion Variational Autoencoder, CDVAE)[327]通过提出噪声条件评分网络，同时利用排列、平移、旋转和周期不变性，将稳定性作为一种归纳偏差。Luo等人(2022)[196]模拟具有等变扩散的互补决定区域的序列和结构，并明确靶向特定抗原结构以产生原子分辨率的抗体。
Medical Image Reconstruction.
反问题是从观测测量中恢复未知信号，这是计算机断层扫描(CT)和磁共振成像(MRI)医学图像重建中的一个重要问题[47,48,230,284,328]。Song等人(2021)[284]利用基于分数的生成模型来重建与先前和观察到的测量一致的图像。Chung等人(2022)[49]训练具有去噪分数匹配的连续时间依赖分数函数，并在数值SDE求解器和数据一致性步骤之间迭代，在评估阶段进行重建。Peng等人(2022)[230]在给定观测到的k空间信号的情况下，通过逐步引导逆扩散过程进行MR重构，并提出了一种从粗到精的采样算法，以实现高效采样。
Future Directions
扩散模型的研究还处于起步阶段，在理论和实证方面都有很大的改进空间。正如前面章节所讨论的，关键的研究方向包括高效采样和改进的似然，以及探索扩散模型如何处理特殊的数据结构，如何与其他类型的生成模型接口，以及如何针对一系列应用进行定制。此外，我们预计未来对扩散模型的研究可能会扩展到以下途径。
Revisiting Assumptions. 扩散模型中的许多典型假设需要重新审视和分析。例如，扩散模型的前向过程完全抹去数据中的任何信息并使其等同于先验分布的假设可能并不总是成立。在现实中，信息的完全去除是不可能在有限的时间内实现的。了解何时停止前向噪声处理以在采样效率和样本质量之间取得平衡是非常有趣的[79]。最近在Schrödinger桥梁和最优运输方面的进展[41,55,57,269,278]提供了有希望的替代解决方案，提出了能够在有限时间内收敛到指定先验分布的扩散模型的新公式。
Theoretical Understanding. 扩散模型已经成为一个强大的框架，特别是在大多数应用中，它是唯一一个可以与生成对抗网络(GANs)竞争而无需诉诸对抗训练的框架。利用这种潜力的关键是理解扩散模型在特定任务中为何以及何时比替代方案更有效。确定扩散模型与其他类型的生成模型(如变分自编码器、基于能量的模型或自回归模型)的基本特征是很重要的。理解这些区别将有助于阐明为什么扩散模型能够在获得最高似然的同时生成高质量的样本。同样重要的是，需要为系统地选择和确定扩散模型的各种超参数提供理论指导。
Latent Representations. 与变分自编码器或生成对抗网络不同，扩散模型在其潜在空间中提供数据的良好表示效果较差。因此，它们不能很容易地用于诸如基于语义表示操作数据之类的任务。此外，由于扩散模型中的潜在空间通常与数据空间具有相同的维数，因此采样效率受到负面影响，模型可能无法很好地学习表示方案[132]。
AIGC and Diffusion Foundation Models. 从稳定扩散到ChatGPT，人工智能生成内容(Artificial Intelligence Generated Content, AIGC)得到了学术界和工业界的广泛关注。生成式预训练是GPT-1/2/3/4[220, 224, 241, 242]和(Visual) ChatGPT[316]的核心技术，它配备了大型语言模型(Large Language Models, 大型语言模型)[296]和Visual Foundation Models[24, 360, 363]，显示出良好的生成性能和惊人的突发能力[314]。将生成式预训练(仅解码器)从GPT系列转移到扩散模型类，在规模上评估基于扩散的生成性能，并分析扩散基础模型的应急能力是一个有趣的研究。此外，将大型语言模型与扩散模型相结合已被证明是一个新的有前途的方向[347,349]。
CONCLUSION
我们已经从各个角度全面地介绍了扩散模型。我们首先介绍了三个基本公式:ddpm、sgm和Score sde。然后，我们讨论了最近改进扩散模型的努力，强调了三个主要方向:采样效率、似然最大化和具有特殊结构的数据的新技术。我们还探讨了扩散模型和其他生成模型之间的联系，并概述了将两者结合起来的潜在好处。对六个领域的应用进行的调查表明，扩散模型具有广泛的潜力。最后，我们概述了未来研究的可能途径。