寒假学习笔记【匠心制作，图文并茂】——1.20拓扑、强连通分量、缩点

前言

更新的稍微有点晚……

因为强连通分量这一块难学且知识点多，学习时间久了亿点，所以直到现在才更新。

拓扑排序

OI-Wiki 是这么定义拓扑排序的：

拓扑排序（Topological sorting）要解决的问题是如何给一个有向无环图的所有节点排序。

这个感觉不是很像定义，更像是它在干什么，我们来重新定义一下拓扑排序：

拓扑排序是一种将一个有向无环图（Directed Acyclic Graph，简称 DAG）按照一定顺序对所有节点进行排序的算法。

注意：只能在有向无环图上跑拓扑。

拓扑排序是怎么运作的

接下来我就要开始操作了，注意步骤：

1. 取出图中入度为 $0$ 的点，加入队列。
2. 取出队头，将与队头相连的点的入度全减 $1$。
3. 将图上入度为 $0$ 的点加入队列。
4. 重复执行 $2$、$3$ 操作。
5. 想你的诗和远方吧……

没看明白的观众就请看下面的模拟，看明白了的，也还是看一下案例吧。

我们先随机生成一个 DAG：

首先按照第一步：取出图中入度为 $0$ 的点并放入队列（如果你连入度是啥都不知道，那你就不应该出现在这）。图中入度为 $0$ 的点不就是 $1$ 吗？此时队列中有一个 $1$。

然后进行第二步：取出队头，将与队头相连的点的入度全减 $1$。队头就是 $1$，那么我们取出 $1$ 并将所有与队头相连的点入度减 $1$，整张图就相当于变成了这样：

队列此时为空。

然后进行第三步：将图上入度为 $0$ 的点加入队列。图上入度为 $0$ 的点有 $2$ 和 $3$，所以把它们加入队列，于是队列变成了这样：

然后就是重复执行以上操作……

最后，我们得到的拓扑序就是这三种中的一种：1 2 3 6 4 5、1 3 2 4 6 5、1 3 2 6 4 5。

不难看出，一张图的拓扑序可以有很多个。所以这类题一般都是 SPJ（Special Judge）。

以 洛谷 B3644 为例，代码如下：

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,rd[106];
vector<int>v[106];
queue<int>q;
signed main()
{cin>>n;for(int x,i=1;i<=n;i++)//统计入度{while(cin>>x&&x){v[i].emplace_back(x);rd[x]++;}}for(int i=1;i<=n;i++)//第一步{if(rd[i]==0){q.emplace(i);}}while(!q.empty())//第二、三步{int x=q.front();q.pop();cout<<x<<" ";for(auto i:v[x]){rd[i]--;if(rd[i]==0){q.emplace(i);}}}return 0;
}

拓扑排序的好处

拓扑排序是一种对图的排序，这种排序可以将二维的图转化成一维的线性数组，这更便于我们跑 DP。

强连通分量

在认识强连通分量之前，我们先来认识一下强连通。

强连通是什么

强连通指如果在一个有向图中，任意两个节点都可以连通，那么我们称之为强连通。

强连通分量是什么

强连通分量（Strongly Connected Components，简称 SCC）指极大的强连通子图。意思就是说对于一个有向图，如果它的其中一个子图是强连通，并且往这个子图里加任何的有向图上的其他点和边它都不再是一个强连通子图，那么我们称之为强连通分量。

比如这个图：

其中点 $1,2,3,4$ 就构成了一个强连通子图，但如果我往这里面加 $5,6$ 中的任何一个点，这个子图就不再是强连通子图，所以点 $1,2,3,4$ 就构成了一个强连通分量。

（为了防止作者被累死，后面所有的“强连通分量”都简写为“SCC”。）

如何求 SCC

这里我讲一下最出名的 Tarjan 算法。

Tarjan 的思路其实很简单，就是把一个图看作一棵奇怪的树。

这里我们随机生成一颗树：

但是我们原本是一张图不是一颗树啊，所以这里必然有一些奇怪的边出来：

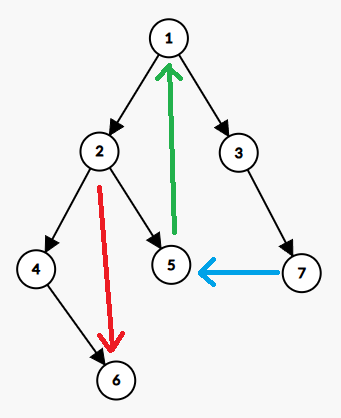
其中这些边我们大致可以分为四类：树边（黑色线）、前向边（红色线）、返祖边（绿色线）、横叉边（蓝色线）。

相信大家通过这张图一定能很好的理解这四种边的定义。

树边：构成树的边。

前向边：从某个根节点到其子节点的边。

返祖边：从某个子节点到其根节点的边。

横叉边：从某个子节点到另一个与它毫无关系的子节点的边。

这里我说明一下：所有的横叉边都只会是向左的。因为所有可能向右的横叉边都会被拿来当成树边，那么另一条边就成了向左的横叉边。

因为我们要找 SCC，也就相当于要在这张图上找环（因为一个环就是一个 SCC），那我们看除了树边以外的其他特殊边那些可能产生环呢？

答案很简单，就是返祖边和横叉边（从图上也能看出来）。

返祖边容易形成环是因为返祖边能返回去，而树边则可以走下来，这样就形成了一个环。横叉边容易形成环是因为它可以连接左右两棵子树，更容易搭建起环，它一般不会直接形成环，而会间接的促成环。

接着我们来看一下这两种边都有什么共同点。不难发现，这两种边的终点都是比起点先被扫描的点。

到这里，Tarjan 老爷子就想通了一切：定义两个数组 dfn[x] 和 low[x] 表示第 $x$ 个节点被扫描时的编号与 $x$ 所能到达的所有点中 dfn 最小的点。

这么定义有什么好处呢？好处可大了！我们假设一个节点与它的子树形成了一个 SCC，那么它以及它的所有子树都不会通过返祖边与横叉边与其他点相连，而且一定会有返祖边与这个根节点相连，所以这个 SCC 里的所有点的 low 都是这个根节点的 dfn，等到递归回到根节点时一查，发现 low==dfn，这下就说明它的所有子节点都无法通过返祖边与横叉边与其他点相连，那就说明这里就是一个 SCC，把它及它的子节点全部保存在一起就行了。

为了方便保存，Tarjan 老爷子还十分聪明的使用了桟来记录当前的访问过的点，这样取出 SCC 时就只需要一直弹出栈顶了。

以 洛谷 B3609 为例题，代码如下：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std;
code by plh
int n,m,cnt,ti,dfn[10006],low[10006],ins[10006],b[10006],vis[10006],belong[10006];
vector<int>v[10006],vv[10006];
stack<int>st;
void tarjan(int x)
{dfn[x]=low[x]=++ti;//记录编号st.emplace(x);ins[x]=1;for(auto i:v[x]){if(!dfn[i]){tarjan(i);low[x]=min(low[x],low[i]);//更新}else if(ins[i]){low[x]=min(low[x],dfn[i]);}}if(low[x]==dfn[x])//找到 SCC{cnt++;while(1){int u=st.top();st.pop();ins[u]=0;belong[u]=cnt;//记录下来每个点属于哪个 SCC（主要是为了缩点）b[u]=cnt;vv[cnt].emplace_back(u);//记录下来有哪些点if(u==x){break;}}}
}
signed main()
{cin>>n>>m;for(int x,y,i=1;i<=m;i++){cin>>x>>y;v[x].emplace_back(y);}for(int i=1;i<=n;i++){if(!dfn[i]){tarjan(i);}}for(int i=1;i<=cnt;i++){sort(vv[i].begin(),vv[i].end());}cout<<cnt<<endl;for(int i=1;i<=n;i++){if(!vis[b[i]]){for(auto j:vv[b[i]]){cout<<j<<" ";}cout<<endl;vis[b[i]]=1;}}return 0;
}

缩点

讲完强连通分量，我们就可以来好好讲讲缩点了。

缩点，就是把一个 SCC 看作一个点并构建新图，这样做的好处就在于它会形成一个新的 DAG（并且还能优化时间复杂度），便于我们跑拓扑与 dfs。

代码其实很简单，就是用上述的 belong 数组进行操作：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std;
code by plh
int n,m,ti,cnt,dis[10006],rd[10006],a[10006],b[10006],belong[10006],dfn[10006],low[10006],ins[10006];
vector<int>v[10006],vv[10006];
stack<int>st;
map<pair<int,int>,bool>mp;
queue<int>q;
void tarjan(int x)//跑 tarjan
{dfn[x]=low[x]=++ti;st.emplace(x);ins[x]=1;for(auto i:v[x]){if(!dfn[i]){tarjan(i);low[x]=min(low[x],low[i]);}else if(ins[i]){low[x]=min(low[x],dfn[i]);}}if(low[x]==dfn[x]){++cnt;while(1){int u=st.top();st.pop();ins[u]=0;belong[u]=cnt;b[cnt]+=a[u];if(u==x){break;}}}
}
int topsort()//拓扑排序
{for(int i=1;i<=cnt;i++){if(!rd[i]){q.emplace(i);dis[i]=b[i];}}while(!q.empty()){int x=q.front();q.pop();for(auto i:vv[x]){dis[i]=max(dis[i],dis[x]+b[i]);rd[i]--;if(!rd[i]){q.emplace(i);}}}int ans=0;for(int i=1;i<=cnt;i++){ans=max(ans,dis[i]);}return ans;
}
signed main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1,x,y;i<=m;i++){cin>>x>>y;v[x].emplace_back(y);}for(int i=1;i<=n;i++){if(!dfn[i]){tarjan(i);}}for(int i=1;i<=n;i++)//建新图{for(auto j:v[i]){if(belong[i]!=belong[j]&&!mp[make_pair(belong[i],belong[j])])//这里有时需要判重，有时又不需要，主要是看重边会不会有影响//如果只是单纯跑拓扑是没有什么影响的，但如果要做与边相关的运算就有影响了{vv[belong[i]].emplace_back(belong[j]);rd[belong[j]]++;mp[make_pair(belong[i],belong[j])]=1;}}}cout<<topsort();return 0;
}