Dijkstra 算法求解多种操作
一、问题背景与核心需求
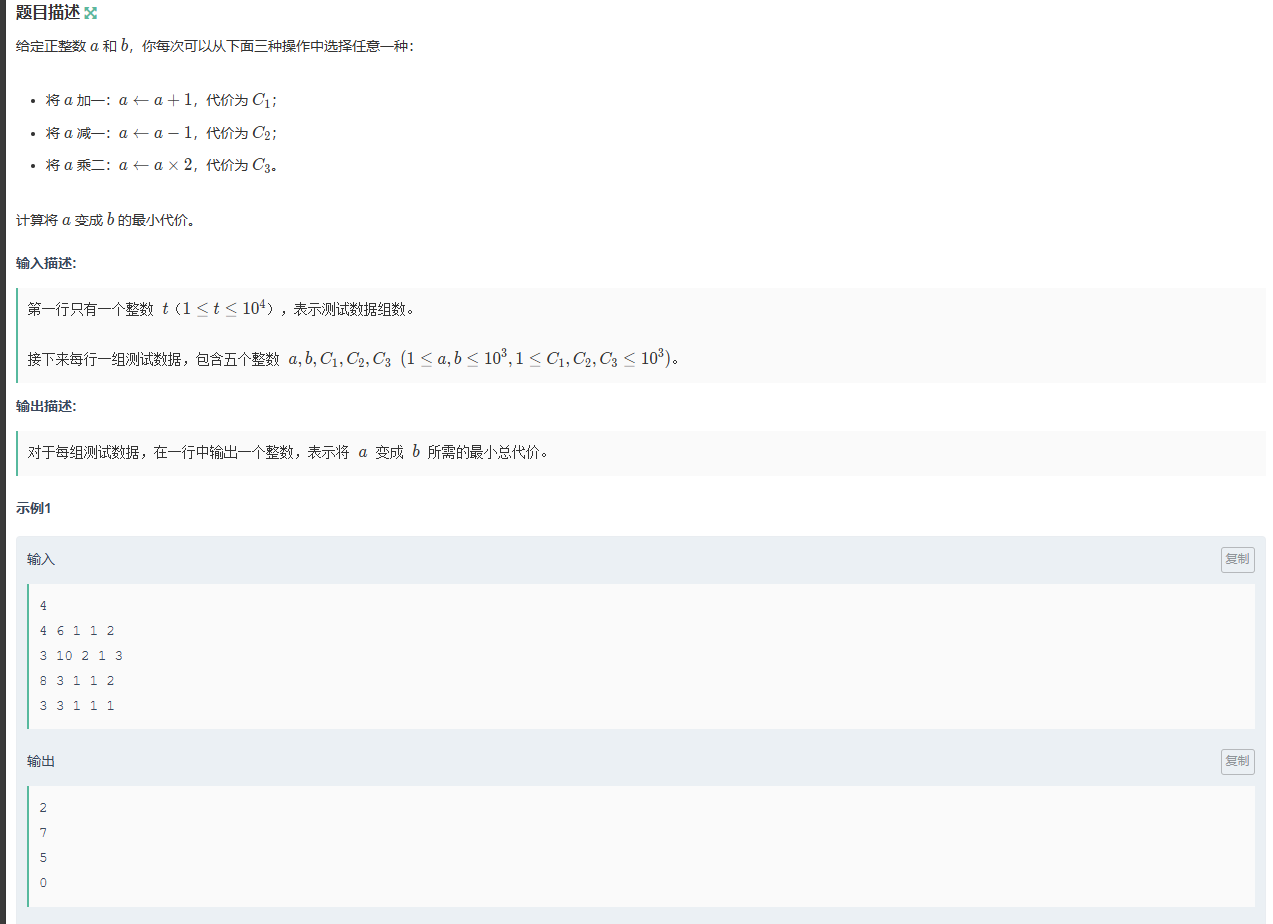
需要找到从a到b的最优操作序列,使得总花费最小。三种操作的规则为:
- 操作 1:
x → x+1,花费c1; - 操作 2:
x → x-1,花费c2; - 操作 3:
x → x*2,花费c3。
例如:若a=7,b=9,c1=1000,c2=1,c3=1,最优路径可能是7→5→10→9(先减 2 次到 5,乘 2 到 10,再减 1 到 9),总花费2*c2 + c3 + c2,比直接加 2 次(2*c1)更便宜。
我们发现,路径的选择是非常多种多样的,无法靠人力去完整的思考有哪些可能。
二、算法选择与设计
1. 问题转化为图论模型
将每个整数视为节点,每种操作视为有向边(边权为操作花费)。例如:
- 节点
x到x+1有一条边,权值c1; - 节点
x到x-1有一条边,权值c2; - 节点
x到2x有一条边,权值c3。
问题转化为:在该图中寻找从节点a到节点b的最短路径(总权值最小)。
Dijkstra 算法求解单源最短路径
2. 为何用 Dijkstra 算法?
Dijkstra 算法#图论-CSDN博客
- 所有操作的花费(边权)均为非负数(题目隐含
c1,c2,c3≥0),无负权边; - Dijkstra 算法适合求解单源最短路径(从
a到b),且在非负权图中效率高。
3. 搜索范围的确定(limit = max(a,b)*2)
需要限制节点范围,否则节点可能无限大(如多次乘 2)。选择max(a,b)*2的原因:
- 最优路径可能需要 “超过
b再返回”,例如a=7→5→10(>9)→9(b=9); max(a,b)*2足够覆盖此类情况,避免遗漏最优路径。
三、代码细节解析
1. 特殊情况处理(a > b)
当a > b时,加 1 或乘 2 会使a更大,远离b,最优策略只能是持续减 1,因此直接计算花费:(a - b) * c2。
2. Dijkstra 算法实现
- 距离数组
dist:dist[v]表示从a到v的最小花费,初始化为inf(无穷大),dist[a] = 0(起点花费为 0)。 - 优先队列
pq:小根堆(按花费升序),存储(当前花费, 节点),每次取出花费最小的节点处理。 - 邻接点生成:对当前节点
u,生成三个邻接点:u+1(花费c1);u-1(花费c2);u*2(花费c3)。
- 松弛操作:若通过
u到达v的花费(curdist + w)小于已知最小花费dist[v],则更新dist[v]并加入队列。
3. 终止条件
当队列中取出的节点为b时,说明已找到a到b的最短路径,可直接退出循环。
四、示例说明
以a=7,b=9,c1=1000,c2=1,c3=1为例:
- 节点范围
limit = max(7,9)*2 = 18,覆盖可能的路径节点(如 10)。 - 初始
dist[7] = 0,队列加入(0,7)。 - 处理节点 7 时,邻接点为 8(花费 1000)、6(花费 1)、14(花费 1),更新对应
dist并加入队列。 - 后续处理节点 6(花费 1),邻接点 5(花费 1+1=2)、7(已处理)、12(花费 1+1=2)。
- 处理节点 5(花费 2),邻接点 6(花费更高,跳过)、4(花费 3)、10(花费 2+1=3)。
- 处理节点 10(花费 3),邻接点 11(花费 3+1000)、9(花费 3+1=4),此时
dist[9] = 4,找到目标,退出。
最终输出4,符合最优路径花费。
五、码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;const ll inf = 0x3f3f3f3f3f3f3f3f; // 定义无穷大// 解决从数字a变为b的最小花费问题
void solve() {ll a, b, c1, c2, c3;cin >> a >> b >> c1 >> c2 >> c3;// 当a大于b时,只能不断减1,直接计算花费if (a > b) {cout << (a - b) * c2 << '\n';return;}// 确定搜索的上限:覆盖可能需要超过b再返回的情况ll limit = max(a, b) * 2;// 初始化距离数组,dist[x]表示从a到x的最小花费vector<ll> dist(limit + 1, inf);// 优先队列,按花费从小到大排序priority_queue<pair<ll, ll>, vector<pair<ll, ll>>, greater<>> pq;// 起点a的花费为0dist[a] = 0;pq.emplace(0, a);// Dijkstra算法主循环while (!pq.empty()) {// 取出当前花费最小的节点auto [curdist, u] = pq.top();pq.pop();// 到达目标值b,输出结果并终止if (u == b)break;// 跳过已处理的过时路径if (curdist > dist[u])continue;// 生成三种操作对应的邻接点和边权vector<pair<ll, ll>> adj = {{u + 1, c1}, // 操作1:加1,花费c1{u - 1, c2}, // 操作2:减1,花费c2{u * 2, c3} // 操作3:乘2,花费c3};// 遍历所有邻接点,进行松弛操作for (auto [v, w] : adj) {// 检查节点范围并更新最短路径if (1 <= v && v <= limit) {ll newdist = curdist + w;if (newdist < dist[v]) {dist[v] = newdist;pq.push({newdist, v});}}}}// 输出到达b的最小花费cout << dist[b] << '\n';
}int main() {// 优化输入输出效率ios::sync_with_stdio(false);cin.tie(nullptr);ll t = 1;cin >> t;while (t--)solve();
}