当前位置：首页 > news >正文

leetcode - 前缀和

news 来源：原创 2025/5/25 5:28:47

系列文章目录

leetcode - 双指针问题_leetcode双指针题目-CSDN博客

leetcode - 滑动窗口问题集_leetcode 滑动窗口-CSDN博客

高效掌握二分查找：从基础到进阶-CSDN博客

前言

1、题1 【模板】前缀和：

解法一：暴力解法

解法二：前缀和

参考代码：

2、题2 【模板】二维前缀和：

解法一：暴力解法

解法二：前缀和思想

1、预处理

2、使用该前缀和矩阵

参考代码：

3、题3 寻找数组的中心下标：

解法一：暴力解法

解法二：前缀和 & 后缀和

步骤一：预处理前缀和数组

步骤二：使用前缀和数组

步骤三：细节处理

参考代码：

题4 除自身以外数组的乘积：

解法一：暴力解法

解法二：前缀和&后缀和

参考代码：

题5 和为 K 的子数组：

解法一：暴力解法

解法二：

参考代码：

题6 和可被 K 整除的子数组：

解法一：暴力枚举

解法二：前缀和+哈希表

参考代码：

题7 连续数组：

解法一：前缀和+哈希表

参考代码：

题8 矩阵区域和：

思考：

参考代码：

总结

前言

路漫漫其修远兮，吾将上下而求索；

这是所有题目的汇总，大家可以先尝试做一下~

DP34 【模板】一维前缀和
DP35 【模板】二维前缀和
724. 寻找数组的中心下标
238. 除自身以外数组的乘积
560. 和为 K 的子数组
974. 和可被 K 整除的子数组
525. 连续数组
1314. 矩阵区域和

1、题1 【模板】前缀和：

【模板】前缀和_牛客题霸_牛客网

思考：

解法一：暴力解法

从下标l 处开始遍历相加到下标为r 的下标处；即要求哪段区间的和，就直接暴力遍历相加这段区间中的数据即可；

本题的数据量很大，暴力解法是一定会超时的；

解法二：前缀和

前缀和，专门用来解决一类问题：快速地得到某一段连续区间的和；

前缀和一般分两步进行：

1、预处理出来一个前缀和数组
2、使用该前缀和数组

对于“预处理出来一个前缀和数组”，其实就是dp 动态规划的思想，步骤如下：

1、创建一个和原数组同等规模的数组 dp
2、dp[i] 表示 [1，i] 区间（第1个数据到第i个数据）中所有所有数据的和；

图解如下:

即dp[i] = dp[i-1] + nums[i]

“使用前缀和数组”：

而对于处理每一次的询问[l,r] 可以转换为：dp[lr] = dp[r] - dp[l-1],如下图：

显然，我们可以根据 dp[r] 和 dp[l-1] 计算得到我们想要的答案；

Q1：为什么下标要从1开始？

读题干可以得知，此处的下标只能从1开始；况且，倘若下标从0开始，当我有一次想询问 [0,4] 这段区间的时候，带入我们计算的式子： dp[lr] = dp[r] - dp[l-1] ，就为 dp[lr] = dp[4] - dp[-1];下标为-1就是越界访问，所以当出现这样的情况需要特殊处理；

但是下标从1开始就没有这样的问题，eg, 循环区间 [1,7] --> dp[lr] = dp[7] - dp[0]; 倘若题干中的下标从0开始，我们还可以在其数组前面增加一个虚拟结点，让其数据从下标为1的地方开始，这样算就规避了边界情况；

参考代码：

#include <iostream>
#include<vector>
using namespace std;int n , m, l ,r;void del(vector<long long>& dp)
{cout<<dp[r]-dp[l-1]<<endl;
}int main() 
{//dp[i] 下标[1,i] 的数据和//1、输入cin>>n>>m;vector<int> nums(n+1);for(int i = 1;i<=n;i++) cin>>nums[i];//2、创建dp 表vector<long long> dp(n+1);//使用long long 防止溢出for(int i = 1;i<=n;i++){dp[i] = dp[i-1]+nums[i];}//3、处理询问while(m){cin>>l>>r;//处理del(dp);m--;}return 0;
}

2、题2 【模板】二维前缀和：

【模板】二维前缀和_牛客题霸_牛客网

思考：

本题和上一道题一样，本题题干中有明显地提示“下标从1开始”；

解法一：暴力解法

模拟实现即可；时间复杂度为O(n*m*q) ，而数据量也不少，暴力解法一定会超时；

解法二：前缀和思想

分两步解决：

1、预处理出来一个前缀和矩阵

2、使用该前缀和矩阵

1、预处理

首先是需要创建一个和原二维数组同等规模的二维数组（但是为了避免计算过程中的越界问题，会增加一行一列），其次是 dp[i][j] 表示从 [1,i] 到 [i, j] 位置，这个矩阵中所有数据之和；

Q：如何快速求出dp[i][j] 中的数据？

dp[i][j] = A + B + C + D;实际上D就是nums[i][j] ，而A就是dp[i-1][j-1];

Q: B、C如何解决呢？

上图中，蓝色区域包含了 B与C以及两个A；即 B+C = dp[i][j-1] + dp[i-1][j] - 2*A;

综上，dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + nums[i][j] ；

2、使用该前缀和矩阵

目标：求得[x1,y1]~[x2,y2] 间数据的总和；

即，涂颜色区域D为我们所求的目标；

我们可以运用上面曾经用过的思想， D = A + B + C + D - (A + B ) - (A + C ) + A

即 D = dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1];

参考代码：

#include <iostream>
#include<vector>
using namespace std;int main() {//1、输入int n, m, q, x1, y1, x2, y2;cin >> n >> m >> q;vector<vector<int>> nums(n + 1, vector<int>(m + 1));for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> nums[i][j];//2、创建dpvector<vector<long long>> dp(n + 1, vector<long long>(m + 1));for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + nums[i][j];while (q) {cin >> x1 >> y1 >> x2 >> y2;//3、处理,使用dplong long ret = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 -1];cout << ret << endl;q--;}return 0;
}

3、题3 寻找数组的中心下标：

724. 寻找数组的中心下标 - 力扣（LeetCode）

思考：

题干的意思：找到一个下标，其左边的数据之和等于其右边的数据之和；

解法一：暴力解法

枚举每一个下标，然后遍历计算这个下标左右区间中的数据之和比较它们是否相等；时间复杂度为O(N^2)

在暴力解法的基础上进行优化；

解法二：前缀和 & 后缀和

本题需要前缀和、后缀和两个一起使用；前缀和的思想表示从第一个元素开始到第i 个元素上的所有数据的和，后缀和则就表示从最后一个位置开始到当前第i 个位置所有数据的和；

此处我们用 f 、g 分别来表示前缀和、后缀和数组；

f[i] : 从前面第一个数据加到第 i-1 个数据之和；
g[i] ：从最后一个数据加到 i+1 个数据之和；

步骤一：预处理前缀和数组

遍历原数组：

前缀和：f[i] = f[i-1] + nums[i-1];

后缀和: g[i] = g[i+1] + nums[i+1];

步骤二：使用前缀和数组

从 0~n-1 枚举所有的下标，并判断f[i] 与 g[i] 是否相等即可；

步骤三：细节处理

初始化问题：f 、 g 均多开辟了一个位置；填f[0] 时会发生越界访问，故而直接将f[0] 初始化为0即可；对于 g 来说，填 g[n-1] 的时候会发生越界访问，那么直接将g[n-1] 初始化为0即可；

填表顺序：当我们在填f 这个表的时候，我们是：f[i] = f[i-1] + nums[i-1]; 所以 f 表应该从左往右填；当我们在填 g 这个表的时候，我们是：: g[i] = g[i+1] + nums[i+1]; 所以g 表的填表顺序为从右往左；

参考代码：

    int pivotIndex(vector<int>& nums) {int n = nums.size();//前缀和以及后缀和//f[i] : 从第一个数据加到 i-1//g[i] : 从最后一个数据加到 i+1 vector<int> f(n),g(n);//1、初始化f[0] = 0, g[n-1] = 0;//2、填表for(int i = 1; i<n;i++) f[i] = f[i-1] + nums[i-1];for(int i = n-2;i>=0;i--) g[i] = g[i+1] + nums[i+1];//3、使用前缀和、后缀和for(int i = 0; i<n;i++){if(g[i] == f[i]) return i;}return -1;}

题4 除自身以外数组的乘积：

238. 除自身以外数组的乘积 - 力扣（LeetCode）

思考：

解法一：暴力解法

从前往后，边枚举位置边计算除了当前数据之外的乘积，时间复杂度为O(N^2)；

假设枚举到下标i 的位置，要么所求就是区间 [0,i-1] 中所有数的乘积再乘以区间 [i+1,n-1] 中所有数据的乘积；

解法二：前缀和&后缀和

需要创建两个dp 数据: f 、g

f[i] 表示从[0,i-1] 中所有数据之间的乘积
g[i] 表示从 [i+1,n-1] 中所有数据之间的乘积

那么 f[i] = f[i-1] * nums[i-1], g[i] = g[i+1]*nums[i+1];

返回值answer[i] = f[i] * g[i];

细节处理：

1、初始化：当下标为0的时候，0-1=-1,越界了，且下标为0在 f 中意味着，下标0之前所有数据的乘积，而显然下标0之前没有数据。故而f[0] 应该初始化为1；而当下标为n-1的时候，对于 g 来说，n-1+1=n就越界了，且下标为n-1在g 中意味着，下标 n-1 之后所有数间的乘积，但是下标 n-1 之后没有数据了，所以g[n-1]应该初始化为1；

2、填表顺序；对于 f 来说，每次填表均会依靠左边已有的数据，所以填表顺序为从左往右，而对于 g 来说，每次填表均会依靠右边已有的数据，所以g 表填表的数据为从右往左；

参考代码：

    vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();//前缀和、后缀和//f[i] : [0,i-1] 之间的数据乘积//g[i] : [i+1,n-1]之间的数据乘积vector<int> f(n),g(n);//1、初始化f[0] = 1, g[n-1] =1;//f 从左往右,g 从右往左//2、填表for(int i = 1;i<n;i++) f[i] = f[i-1]*nums[i-1];for(int i = n-2;i>=0;i--) g[i] = g[i+1]*nums[i+1];//3、使用f、gvector<int> answer(n);for(int i = 0;i<n;i++) answer[i] = f[i]*g[i];return answer;}

题5 和为 K 的子数组：

560. 和为 K 的子数组 - 力扣（LeetCode）

思考：

子数组：连续数据；

解法一：暴力解法

从下标为0开始枚举位置，依次计算这个位置往后区间之和（需要一直到n-1），并且与k 相比较，其中利用计数器来计数符合条件的子数组的个数；时间复杂度为O(N^2)；

因为数据包含了正数、0、负数，数据不具有单调性就不能用同向双指针滑动窗口来解决；

解法二：

我们可以利用前缀和快速计算出一个区间中所有数的和；枚举一个子数组我们可以以数据头为枚举的依据，也可以以数据尾为枚举的依据；即以某一个位置为起点的所有子数组，以及以某一个位置为结尾的子数组，如下图：

倘若要使用前缀和，最好是采用以数据尾为枚举的依据；那么在枚举的时候，下标 i : 以 i 位置为结尾的所有子数组，我们就要计算出区间 [0,i-1]中有多少个前缀和等于sum[i]-k 的从下标0开始的子数组；

Q：以i 为结尾的子数组该如何查找？

当我们枚举到i 位置的时候，此时便可以通过前缀和的数组直到[0,i] 中的数据总和sum[i]；而此时只需要找到一个区间和为k 就可以了，那么反过来就是找一个区间的和为 sum[i] - k,如下图：

那么此处就可以转换题意，在以i 为结尾的区间中寻找和为sum[i]-k 的以下标0开始的子数组；

倘若直接遍历去查找，那么就和暴力解法没有区别；

Q2：如何快速地找到前缀和为sum[i]-k 的区间？

借助于哈希表来解决，前缀和对应出现的次数；

细节问题：

1、前缀和数据放入hash 中的时机：

一是将前缀和全部计算出来，全部放入hash 表中，但是因为此处我们创建的hash 并没有与下标挂钩，所以就不知道当前和为sum[i]-k 的子数组是否在区间 [0,i] 之中；如果用这种方式创建hash 并且照着我们上述的逻辑去实现，得到的结果势必会重复计算；所以这种方法不可行；

二是，在计算 i 位置之前，哈希表中只保存 [0,i-1] 位置的前缀和，当我们计算完 i 位置之后才把i 位置的前缀和放入哈希表中；这种方式就不会重复计算，可行；

2、不用真的创建一个前缀和数组；

在计算前缀和的时候：dp[i] = dp[i-1] + nums[i]；因为此处我们的使用和计算前缀和可以同步进行，求i 位置的前缀和仅需要直到其前一个位置的前缀和就可以了，没有必要专门创建一个数据来存放对应的前缀和数据，使用一个变量来标记i 位置之前的前缀和为多少，然后记得更新sum 便可，再计算下一次的dp[i] ……

3、如果[0,i] 的前缀和就为k

当枚举到i 位置发现其前缀和就是为 k , 那么接下来便会去 [0,-1]中去找和为0的区间，然而 [0,-1] 本身就不存在；所以我们在创建hash的时候可以将 0 这种情况就先放入，hash[0]=1; 相当于默认有一个前缀和为0的区间；

参考代码：

    int subarraySum(vector<int>& nums, int k) {int n = nums.size();//hash 快速查找unordered_map<int,int> hash;//默认就有一个和为0的前缀和数组hash[0]=1;//以 i 位置为结尾的子数组int sum = 0, ret = 0;for(int i = 0;i<n;i++) {sum+=nums[i];//前缀和“数组”的迭代if(hash.count(sum-k)) ret+=hash[sum-k];//看hash 中有没有sum[i] -k 的子数组//入hashhash[sum]++;}return ret;}

题6 和可被 K 整除的子数组：

974. 和可被 K 整除的子数组 - 力扣（LeetCode）

思考：

解法一：暴力枚举

暴力枚举出所有的子数组，判断该子数组中的数据相加是否能被 k 整除；因为本题的数据有正有负，所以依旧不能使用同向双指针滑动窗口来解决；

解法二：前缀和+哈希表

其实本题思路和上一道题是如出一辙的；

我们需要一个前缀和数组来记录以i 结尾区间中数组的总和；

在此之前，我们先了解两个小知识点：

1、同余定理：

同余定理是一个数学公式；

（a - b ）/p = k ……0 如果a-b 的差能被p 整除，也就是说 k 是一个整数；

那么可以转换成 --> a%p = b%p , 即a除以 p 的余数等于b 除以 p 的余数；

证明：

( a - b ) / p = k;

a - b = p * k;

a = p * k + b; 左右同时被 p 取余

a % p = b % p;

Q：取余的本质是什么？eg. 7%2 = 1;

取余的本质是让7 一直减2，直到最终的结果小于2 为止；也可以理解成去除 7 中有多少个2的倍数；

2、负数%整数 = 负数, 对于负数结果的修正

如果想将负数 % 正数所得到的负数修正为一个正确的正数就需要进行修正；

Q：如何进行修正？

eg. a 为负数， b 为正数

那么 a%p 的结果为负--> 想要将其结果变为正数 --> (a%p+p)p

+p 的目的是为了将负数变为正数，在模上一个p 是为了得到最后模的结果；

综上，再结合同余定理：(a%p+p)%p = (b%p+p)%p;

回到上述的分析之中,我们需要判断 (sum[i]-x)%k 是否等于0，结合上述的两个小知识点就可以转换成： (sum[i]%k + k)%k 是否等于 (x%k+k)%k ；也就是说，需要在区间 [0,i-1] 中有多少个前缀和等于(sum[i]%k + k)%k 的子数组；

注：细节处理：前缀和可能为负数，所以进行了修正处理；

同时，本题与上一题一样，没有必要创建一个前缀和数组，利用一个变量来记录便可，将前缀和数组的余数入哈希表；

细节处理思考：

1、什么时候入哈希表？与上题一样，在计算 i 位置之前，哈希表中只保存 [0,i-1] 位置的前缀和，当我们计算完 i 位置之后才把i 位置的前缀和放入哈希表中；

2、不用真的创建前缀和数组

3、在创建hash的时候可以将 0 这种情况就先放入，hash[0]=1; 相当于默认有一个前缀和为0的区间；

参考代码：

    int subarraysDivByK(vector<int>& nums, int k) {//使用哈希表，提升查找效率unordered_map<int,int> hash;hash[0%k] = 1;//默认有一个前缀和为0的区间//不用真的创建一个前缀和数组，使用变量记录就可以实现int sum = 0, ret = 0;for(auto e: nums) {sum+=e;if(hash.count((sum%k+k)%k)) ret += hash[(sum%k+k)%k];//入hashhash[(sum%k+k)%k]++;}return ret;}

题7 连续数组：

525. 连续数组 - 力扣（LeetCode）

思考：

二进制数组即数组中全为0或者1构成；我们要找含有相同数量0和1的最长连续子数组；

解法一：前缀和+哈希表

一个区间中0和1的数目相等意味着这个区间中数据总和为数据量的一半；这样的话就需要两个维度来统计，一是数据量而是该区间的总和，可以在放入哈希表的时候就判断是否符合条件；即倘若这个区间中数据总和为数据量的一半，就统计个数，这种方法是可行的，但是有两个判断的维度，有点麻烦；

换一个角度思考前缀和重点在于 “和” ，让和作为判断依据，我们可以先遍历一遍数组将0改为-1（也有不改变原数组的方法，只不过需要在取数据的时候进行判断，为0就该加-1；一样的效果，不赘述），那么当区间中的“0” 和 1 的个数相等时，该区间所有数据相加一定为0；那么整个区间和为sum 的话，我们仅需要找到和也为 sum 的前缀和数组，那么就存在以i 为结尾和为0的子数组；

那我们相当于就转换了题意：在数组中找出最长和为0的子数组

细节问题：

1、哈希表中存什么？

本题要求“和为0” 的最长子数组，故而哈希表的第一个参数来记录该数组的和，第二个参数来记录该数组中的数据长度；

2、什么时候存入哈希表？

当当前位置(i)的值与当前位置所绑定的sum 比较完之后，即使用完之后再将当前位置的前缀和存入哈希表；

3、如果有重复的<sum,i> 该怎么办？

当遍历到i 位置时发现前面已经有一个区间的前缀和为sum. 此时 i 位置的前缀和是否需要扔入哈希表？

不需要，因为本题所要的就是求和为0的最长的子数组长度；也就意味着所找的和为sum 的前缀和区间长度越小越好；

所以，如果出现重复的sum , 只保存最小的i ；

4、默认前缀和为0的情况该如何处理？

当我们发现整个数组的和为sum 的时候，此时我们需要在-1 的位置寻找一个前缀和为0的位置；所以hash[0] = -1；为-1，是保证了计算长度时的正确性；

5、区间的长度如何处理？

下标相减，如下：

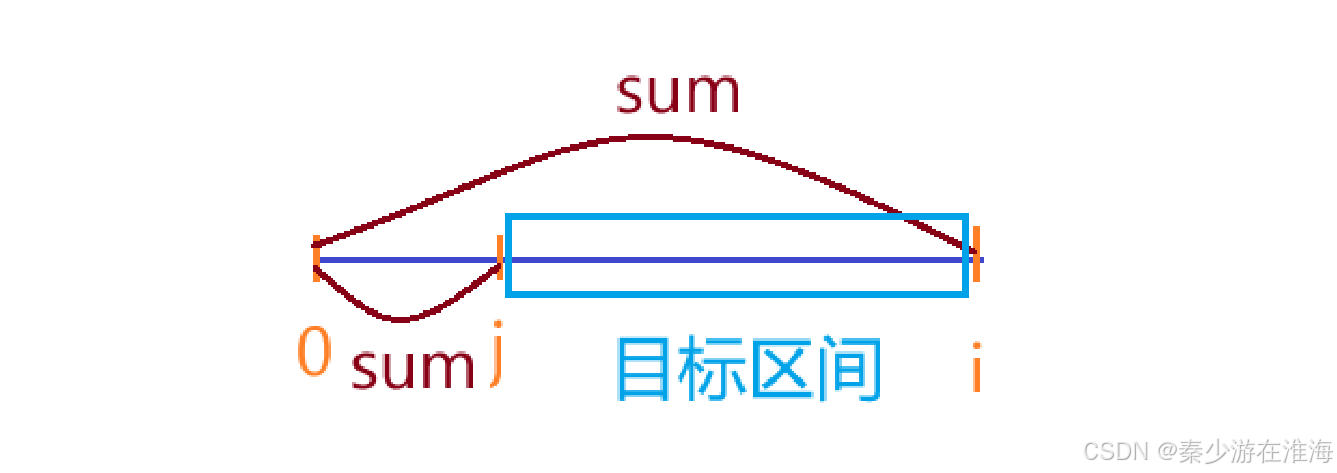
所求区间的长度： i - j;

参考代码：

    int findMaxLength(vector<int>& nums) {int n = nums.size();//首先遍历数组将0改为-1for(auto& e: nums) if(e==0) e = -1;//创建hashunordered_map<int,int> hash;//默认初始化hash[0] = -1;int sum = 0 , ret = 0;for(int i = 0; i<n;i++){sum+=nums[i];//判断sum 是否为0，并且前面是否有0if(hash.count(sum)) ret = max (ret , i - hash[sum]);else hash[sum] = i;}return ret;}

题8 矩阵区域和：

1314. 矩阵区域和 - 力扣（LeetCode）

思考：

本题的题意：以当前格子为中心，求出周围相聚k 个格子的和；

观察例子：

该题的本质：快速地求出矩阵中某个区域地和 --> 使用二维前缀和来解决；

回忆一下二维前缀和：

1、初始化前缀和矩阵： dp[i][j] = dp[i][j-1] + dp[i][j-1] - dp[i-1][j-1] + nums[i][j];
2、使用前缀和矩阵： dp[x1,y1]~[x2,y2] = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];

Q1：answer[i][j] 如何求？

想要求这块区域中的总和，需要知道该区域的左上角以及右下角左边即可；而想要求得answer[i][j] 就要清楚在原始矩阵mat 对应的范围；

细节处理：

1、我们直接根据已知坐标[i,j] 去求得对应的左上角以及右下角坐标是有可能会越界的；

当 i-k、j-k 小于0，是需要回归为0，同理，当i+k,j+k 大于该行该列的最大，也是需要进行回归的；假设行为m ,列为n;

(x1,y1)

x1 = i-k --> x1 = max( i - k , 0)
y1 = j-k --> y1 = max (j - k , 0 )

(x2 , y2)

x2 = i + k --> x2 = min (m-1, i +k)
y2 = j+k --> y2 = min(n-1, j+ k)

Q2: 下标的映射关系

在我们实现二维前缀和模板的时候，为了方便处理边界情况，下标是从1开始的；但是此处下标是从0开始的，我们有两种解决方案；一是将第一行与第一列进行单独的处理，实现起来比较麻烦，但是不用处理dp 与 nums 的下标映射关系；二是在二维前缀和数组前多增加一行一列，实现起来比较麻烦，但是需要处理dp 与 nums 的下标映射关系；

我们此处选择方法二，为dp 数组多开一行一列：

下标的映射关系：

1、初始化为dp 时：因为 dp[1][1] 对应 mat[0][0] --> dp[x][y] = mat[x-1][y-1]，所以 dp[i][j] = dp[i-1][j]+dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1];

2、使用dp 时，answer 也是从下标为0处开始计数的；此处有两种处理方式，一是修改answer[x1,y1]~[x2,y2] = dp[x2+1,y2+1] - dp[x1,y2+1] - dp[x2+1, y1] + dp[x1, y1] ; 二是在求下标的时候就进行映射关系的修改，如下:

(x1,y1)

x1 = i-k --> x1 = max( i - k , 0) + 1
y1 = j-k --> y1 = max (j - k , 0 ) + 1

(x2 , y2)

x2 = i + k --> x2 = min (m-1, i +k) + 1
y2 = j+k --> y2 = min(n-1, j+ k) + 1

参考代码：

    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size() , n = mat[0].size();vector<vector<int>> answer(m,vector<int>(n));//dp vector<vector<int>> dp(m+1, vector<int>(n+1));//多开辟一行以及一列//填dpfor(int i = 1; i<=m;i++){for(int j = 1;j<=n;j++){dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1]; //注意下标的映射关系}}//首先需要求得answer 在 mat 中对应的范围int x1, y1 , x2, y2;//使用dp for(int i = 0; i<m;i++){for(int j = 0;j<n;j++){//处理映射关系x1 = max(0 , i-k) +1 ,y1 = max(0 , j-k) +1;x2 = min(m-1, i+k) +1, y2 = min(n-1, j+k) +1;answer[i][j] = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];}}return answer;}