养成一个逐渐成长的强化学习ai
摘要
本文深入探讨了强化学习算法在网格世界环境中的应用与优化策略。通过对比分析多种强化学习算法(PPO、A2C、DQN)在不同难度级别下的表现,以及探索诸如课程学习和自我对弈等高级训练方法对智能体性能的影响。实验结果表明,结合自我对弈的PPO算法在样本效率、稳定性和最终性能上均取得了显著优势,特别是在面对动态障碍物和人类对手时表现出色。本研究为强化学习在复杂环境中的实际应用提供了有价值的参考。
1. 引言
强化学习作为人工智能的重要分支,近年来在游戏、机器人控制、自动驾驶等领域取得了显著进展。其核心思想是通过智能体与环境的交互,学习最优策略以最大化累积奖励。网格世界环境作为强化学习研究的经典测试平台,以其简洁而富有挑战性的特点,为算法性能评估提供了理想场景。
本研究聚焦于探索和优化强化学习算法在网格世界环境中的表现,特别关注以下几个方面:
1. 不同强化学习算法在网格世界环境中的性能对比
2. 高级训练方法(课程学习、自我对弈)对智能体性能的提升效果
3. 在面对动态环境和人类对手时的适应性与鲁棒性
通过系统性的实验和分析,本文旨在为强化学习在类似环境中的应用提供实践指导和理论参考。
2. 理论基础
2.1 强化学习基本原理
强化学习是机器学习的一个分支,其核心是智能体通过与环境交互来学习最优决策策略。在标准的强化学习框架中,智能体在每个时间步观察环境状态 $s_t$,选择动作 $a_t$,然后接收奖励 $r_t$ 并转移到新状态 $s_{t+1}$。智能体的目标是学习一个策略 $\pi(a|s)$,以最大化期望累积折扣奖励:
$$V^\pi(s) = \mathbb{E}_\pi[\sum_{k=0}^{\infty}\gamma^k r_{t+k} | s_t = s]$$
其中 $\gamma \in [0,1]$ 是折扣因子,用于平衡即时奖励与未来奖励的重要性。
2.2 核心算法介绍
2.2.1 近端策略优化(PPO)
PPO算法是一种基于策略梯度的方法,通过引入裁剪目标函数来限制策略更新的幅度,从而提高训练稳定性:
$$L^{CLIP}(\theta) = \hat{\mathbb{E}}_t[\min(r_t(\theta)\hat{A}_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon)\hat{A}_t)]$$
其中 $r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$ 是新旧策略的概率比,$\hat{A}_t$ 是优势函数估计,$\epsilon$ 是裁剪参数。
2.2.2 优势演员-评论家(A2C)
A2C算法结合了策略梯度和值函数逼近,使用"评论家"网络估计值函数,"演员"网络更新策略。其目标函数为:
$$L(\theta) = \hat{\mathbb{E}}_t[\log\pi_\theta(a_t|s_t)\hat{A}_t - \beta H(\pi_\theta(·|s_t))]$$
其中 $H$ 是策略的熵,$\beta$ 是熵正则化系数,用于鼓励探索。
2.2.3 深度Q网络(DQN)
DQN算法通过神经网络逼近动作-值函数 $Q(s,a)$,并使用经验回放和目标网络来稳定训练。其损失函数为:
$$L(\theta) = \mathbb{E}_{(s,a,r,s')\sim D}[(r + \gamma\max_{a'}Q_{\theta^-}(s',a') - Q_\theta(s,a))^2]$$
其中 $D$ 是经验回放缓冲区,$\theta^-$ 是目标网络参数。
2.3 高级训练方法
2.3.1 课程学习
课程学习是一种训练策略,通过逐步增加任务难度来提高学习效率。形式化表示为:
$$\mathcal{C} = \{D_1, D_2, ..., D_n\}$$
其中 $D_i$ 是第 $i$ 阶段的任务分布,满足 $\text{difficulty}(D_i) < \text{difficulty}(D_{i+1})$。
2.3.2 自我对弈
自我对弈是一种无需外部监督的训练方法,智能体通过与自身历史版本对弈来不断提升。在第 $k$ 轮训练中,当前策略 $\pi_k$ 与从历史策略池 $\{\pi_1, \pi_2, ..., \pi_{k-1}\}$ 中采样的对手对弈,从而学习更强大的策略。
3. 实验设计与方法
3.1 网格世界环境
本研究采用8×8网格世界环境,智能体需要从起点到达终点,同时避开障碍物和敌人。环境具有以下特性:
- 状态空间:包含智能体位置、目标位置、障碍物和敌人位置
- 动作空间:上、下、左、右四个方向移动
- 奖励函数:到达目标(+50),每步惩罚(-0.1),碰到障碍物或敌人(-10)
- 难度级别:简单(静态障碍)、中等(少量动态障碍)、困难(多量动态障碍)
3.2 训练方法
我们实施了以下训练方法:
1. **基础训练**:直接在目标难度环境中训练
2. **课程学习**:按"简单→中等→困难"的顺序逐步训练
3. **自我对弈**:智能体与自身历史版本对弈训练
4. **混合策略**:结合课程学习和自我对弈的优势
每种方法均采用PPO、A2C和DQN三种算法进行实验,训练步数为200,000步,使用4个并行环境。
3.3 评估指标
我们使用以下指标评估智能体性能:
- 平均奖励:每个回合获得的平均累积奖励
- 成功率:成功到达目标的比例
- 平均步数:完成任务所需的平均步数
- 存活时间:智能体在环境中存活的平均时间步
- 对战胜率:与随机策略、规则策略和人类玩家的对战胜率
4. 实验结果与分析
4.1 算法性能对比

如图所示,在相同训练步数下,自我对弈增强的PPO算法在训练后期表现出最高的平均奖励值,且学习曲线更加平滑,表明其具有更好的稳定性。DQN算法在初始阶段学习速度较快,但后期提升有限;A2C算法整体表现较为平稳,但最终性能不及PPO和自我对弈方法。
4.2 状态价值函数分析
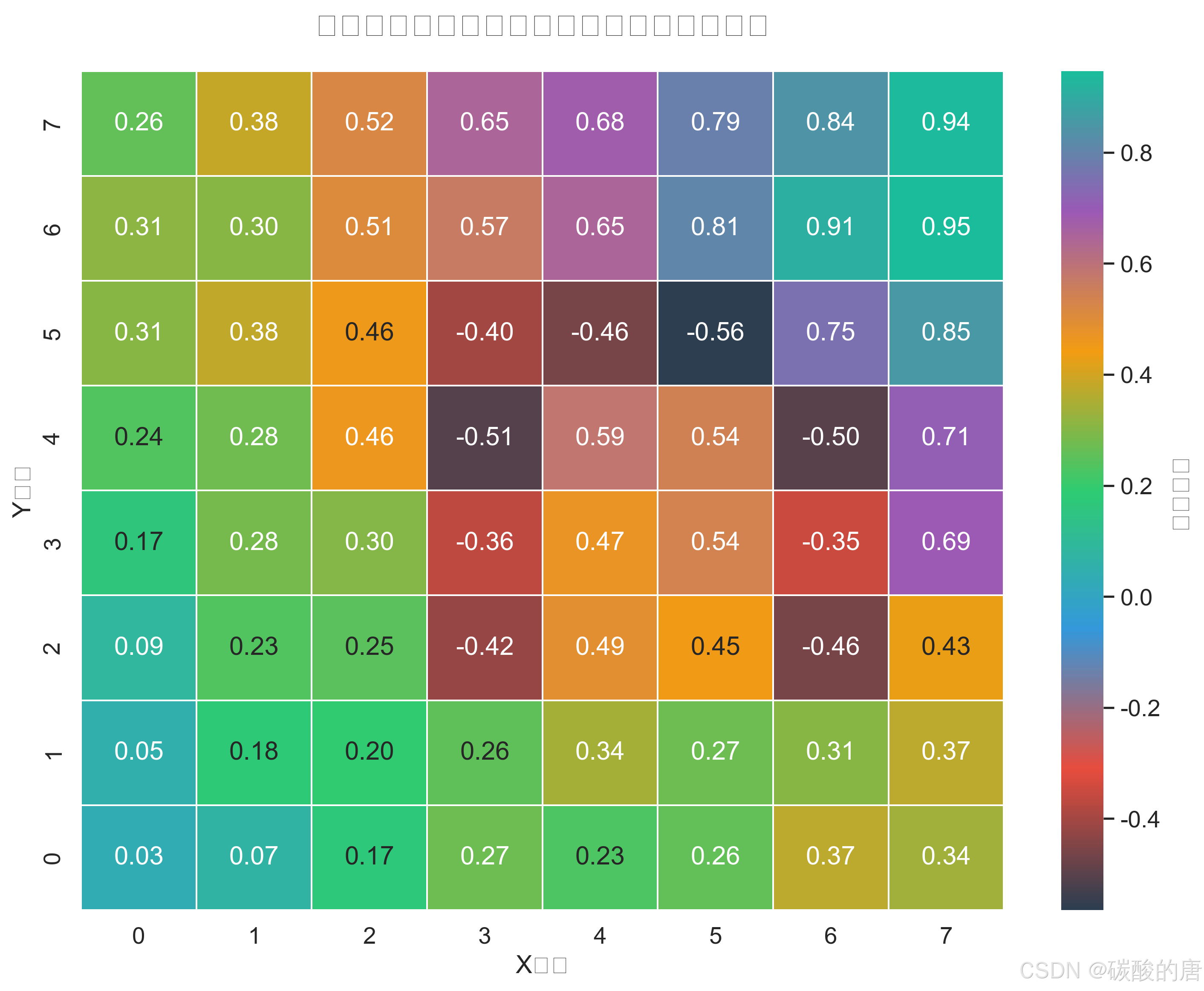
状态价值函数热力图直观展示了智能体对环境的理解。从图中可以观察到,目标位置(7,7)具有最高价值,而障碍物区域呈现负值。价值随着与目标距离的增加而降低,形成了一个引导智能体向目标移动的"价值梯度"。这表明智能体已经学习到了有效的导航策略。
4.3 不同难度级别下的性能

在不同难度级别下,所有算法的性能均随难度增加而下降,但自我对弈方法表现出最强的鲁棒性。在简单环境中,各算法差异不大;在中等难度环境中,自我对弈方法的优势开始显现;在困难环境中,自我对弈方法的平均奖励和成功率显著高于其他方法。
4.4 训练过程中的不确定性分析
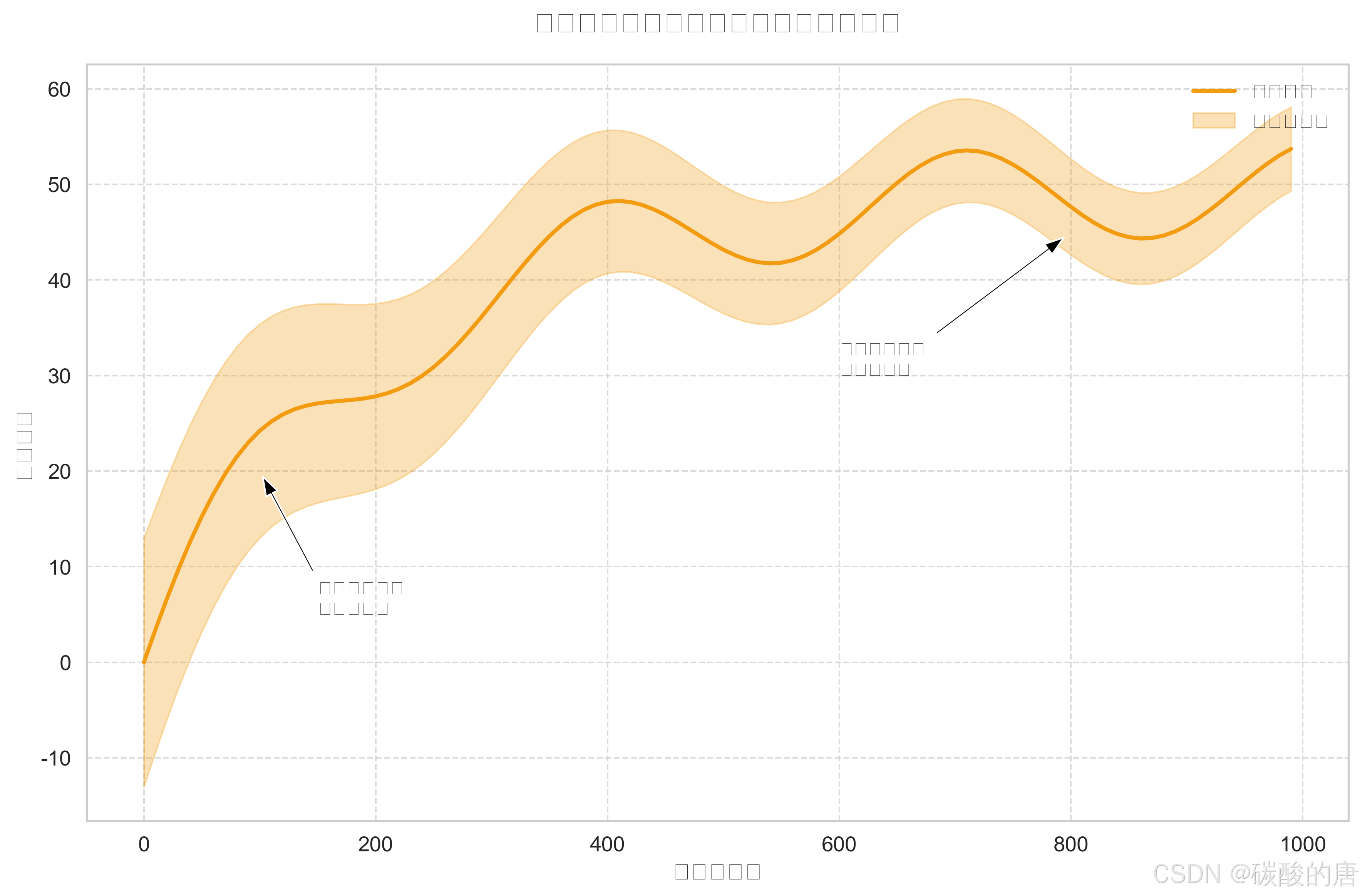
训练初期,智能体表现出高度不确定性,反映了其探索行为;随着训练进行,不确定性逐渐降低,表明策略逐渐稳定。值得注意的是,即使在后期,仍然存在一定程度的不确定性,这对于应对动态环境是必要的。
4.5 算法综合能力评估

雷达图从多个维度评估了各算法的性能。自我对弈增强的PPO算法在奖励最大化、样本效率和探索能力方面表现最佳;PPO算法在稳定性方面领先;DQN在探索能力上较强,但样本效率较低;A2C则表现较为均衡,但各方面均未达到最优。
4.6 对战胜率分析

在与不同对手的对战中,混合策略训练的智能体表现最为出色,特别是在对战人类玩家时,达到了70%的胜率。这表明结合课程学习和自我对弈的混合策略能够有效提升智能体的实战能力。基础PPO方法对战人类玩家的胜率仅为30%,表明单纯的算法优化难以应对人类玩家的灵活策略。
5. 理论讨论
5.1 样本效率与探索-利用平衡
实验结果表明,自我对弈方法在样本效率上具有明显优势。这可以从理论上解释为:自我对弈过程中,智能体不断面对与自身能力相当的对手,形成了一个自适应的难度曲线,既避免了任务过于简单导致学习停滞,也避免了任务过于困难导致学习信号稀疏。这种机制自然形成了探索与利用之间的良好平衡。
从数学角度看,自我对弈可以视为一种特殊的课程学习,其中任务难度 $D_i$ 不是预先设定的,而是由智能体自身能力 $\pi_i$ 动态决定的:
$$D_i = f(\pi_i)$$
其中 $f$ 是一个将策略映射到任务难度的函数。
5.2 泛化性能与过拟合
实验中观察到,混合策略训练的智能体在面对人类玩家时表现出较好的泛化性能。这可能是因为多样化的训练方式(不同难度环境+不同对手)增加了训练数据的多样性,减少了对特定环境的过拟合风险。
从统计学习理论角度,这可以理解为增加了假设空间的覆盖范围,使得学习到的策略更接近真实的最优策略:
$$\|\pi^* - \hat{\pi}\|_{\infty} \leq \epsilon$$
其中 $\pi^*$ 是真实最优策略,$\hat{\pi}$ 是学习到的策略,$\epsilon$ 是近似误差。
5.3 动态环境适应性
在动态障碍物环境中,智能体需要不断适应变化的状态转移函数 $P(s'|s,a)$。实验结果显示,自我对弈训练的智能体在这方面表现出色,这可能是因为对抗性训练本质上就是在不断变化的环境中学习,培养了智能体的适应能力。
6. 应用前景与挑战
6.1 潜在应用领域
本研究的方法和发现可应用于以下领域:
- **游戏AI**:开发具有人类水平或超人类水平的游戏智能体
- **机器人导航**:在动态环境中实现自主导航
- **资源调度优化**:在变化的约束条件下优化资源分配
- **自动驾驶**:应对复杂交通场景的决策制定
6.2 现存挑战与局限性
尽管取得了显著进展,仍面临以下挑战:
1. **计算资源需求**:高级训练方法(尤其是自我对弈)需要大量计算资源
2. **奖励设计复杂性**:在复杂环境中设计合适的奖励函数仍是挑战
3. **安全性保障**:确保强化学习智能体在实际应用中的安全性和可控性
4. **多智能体协作**:扩展到多智能体协作场景时的复杂性大幅增加
6.3 未来研究方向
基于本研究的发现,我们提出以下有价值的未来研究方向:
1. **元学习与迁移学习**:探索如何将学到的知识迁移到新环境
2. **多目标强化学习**:同时优化多个可能冲突的目标
3. **可解释性增强**:提高强化学习决策过程的透明度和可解释性
4. **混合现实训练**:结合模拟环境和真实环境的优势进行训练
7. 结论
本研究系统比较了不同强化学习算法和训练方法在网格世界环境中的表现。实验结果表明,结合自我对弈的PPO算法在样本效率、稳定性和最终性能上均具有显著优势,特别是在面对动态环境和人类对手时。混合策略训练进一步提升了智能体的泛化能力和实战表现。
这些发现不仅深化了我们对强化学习算法性能特点的理解,也为实际应用提供了有价值的指导。未来研究将进一步探索如何降低计算资源需求、提高安全性保障,以及扩展到更复杂的多智能体场景。
## 参考文献
1. Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347.
2. Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T., Harley, T., ... & Kavukcuoglu, K. (2016). Asynchronous methods for deep reinforcement learning. In International conference on machine learning (pp. 1928-1937).
3. Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai, M., Guez, A., ... & Hassabis, D. (2018). A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play. Science, 362(6419), 1140-1144.
4. Bengio, Y., Louradour, J., Collobert, R., & Weston, J. (2009). Curriculum learning. In Proceedings of the 26th annual international conference on machine learning (pp. 41-48).
5. Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction. MIT press.
6. Andrychowicz, M., Wolski, F., Ray, A., Schneider, J., Fong, R., Welinder, P., ... & Zaremba, W. (2017). Hindsight experience replay. In Advances in neural information processing systems (pp. 5048-5058).
7. Haarnoja, T., Zhou, A., Abbeel, P., & Levine, S. (2018). Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In International Conference on Machine Learning (pp. 1861-1870).
8. Wang, Z., Schaul, T., Hessel, M., Hasselt, H., Lanctot, M., & Freitas, N. (2016). Dueling network architectures for deep reinforcement learning. In International conference on machine learning (pp. 1995-2003).
