力扣509题:斐波那契数列的解法与代码注释
小学生一枚,自学信奥中,没参加培训机构,所以命名不规范、代码不优美是在所难免的,欢迎指正
代码是自己写的,文字是AI配的
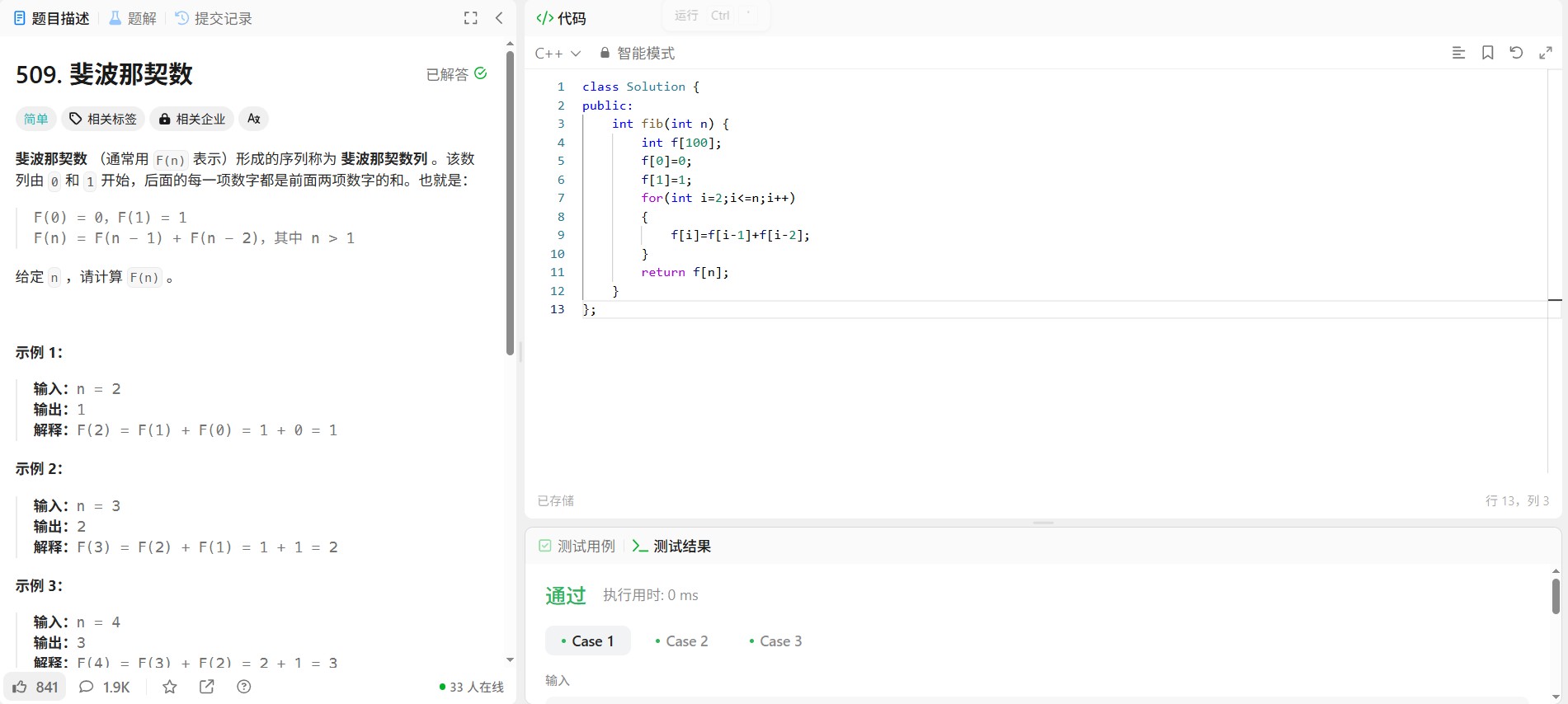
斐波那契数列是一个经典的递归问题,通常用于理解动态规划和递归的基本概念。力扣第509题要求实现一个函数,计算第n个斐波那契数。以下是一个使用动态规划思想的C++解决方案,并附有详细注释。
代码实现
class Solution {
public:int fib(int n) {// 定义一个数组来存储斐波那契数列的值int f[100];// 初始化前两个斐波那契数f[0] = 0;f[1] = 1;// 使用循环计算从第2个到第n个斐波那契数for(int i = 2; i <= n; i++) {f[i] = f[i - 1] + f[i - 2];}// 返回第n个斐波那契数return f[n];}
};
代码解析
-
数组定义:代码中定义了一个大小为100的数组
f,用于存储斐波那契数列的值。这个数组的大小可以根据实际需求进行调整,但需要确保能够存储到第n个斐波那契数。 -
初始化:数组的前两个元素
f[0]和f[1]分别被初始化为0和1,这是斐波那契数列的起始值。 -
循环计算:通过一个
for循环,从第2个斐波那契数开始,依次计算每个斐波那契数,并将其存储在数组中。每个斐波那契数都是前两个数的和。 -
返回结果:最后,函数返回数组中的第n个元素,即第n个斐波那契数。
总结
通过动态规划的方法,可以高效地计算斐波那契数列。代码中的注释和优化建议有助于理解算法的实现细节,并为进一步优化提供了思路。
