【漫话机器学习系列】272.K近邻中K的大小(K-NN Neighborhood Size)
【机器学习】K近邻算法中的K值选择详解:偏差与方差的权衡
在机器学习的众多算法中,K最近邻(K-Nearest Neighbors, 简称 KNN)是一种简单直观却非常实用的分类与回归方法。在实际使用中,我们往往会面临一个重要的参数选择问题:K值的大小该如何设置?
本文将通过一张图深入剖析 K 值的影响,帮助你在实际项目中做出更合理的模型配置决策。
一、什么是 KNN?
KNN 是一种基于“距离”度量的惰性学习算法。其核心思想是:给定一个测试样本,找到训练集中距离它最近的 K 个邻居,根据这些邻居的“投票”结果来决定测试样本的类别或回归值。
KNN 不依赖于显式的训练过程,适用于小数据集,且对特征空间直观有效。然而,这种“简单粗暴”的方法对 K 值非常敏感。
二、图解 K 值的影响
让我们来看一张形象的图(见下图):
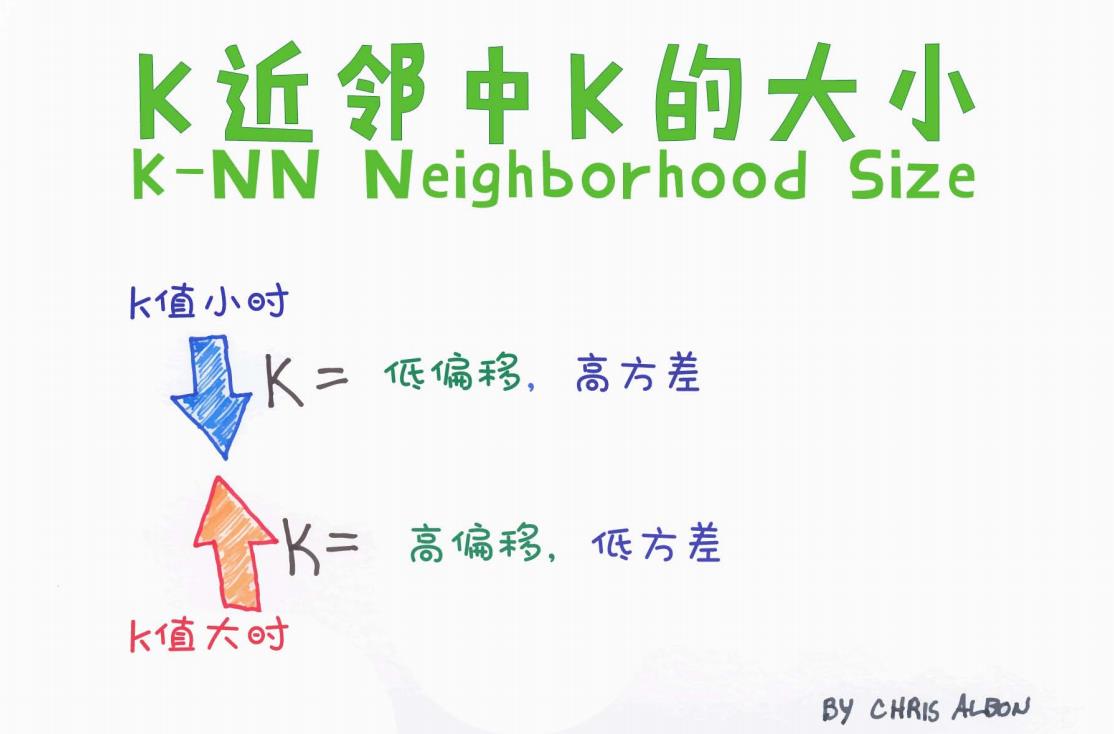
图中通过颜色鲜明的箭头,直观地展示了 K 值变化时模型的偏差(Bias)和方差(Variance)变化情况。
-
当 K 值较小时(图中蓝色向下箭头)
-
模型更加灵活,对训练数据拟合得较好
-
低偏差(Low Bias):因为模型能捕捉到数据的细节
-
高方差(High Variance):对噪声也会“记得太牢”,容易过拟合
-
-
当 K 值较大时(图中红色向上箭头)
-
模型变得平滑,考虑更多邻居的整体趋势
-
高偏差(High Bias):因平滑处理忽略了一些细节,容易欠拟合
-
低方差(Low Variance):模型对输入数据的变化不敏感,泛化能力更强
-
三、偏差-方差权衡(Bias-Variance Tradeoff)
这是机器学习中一个非常核心的概念。KNN 模型中的 K 值恰恰体现了这种权衡关系:
| K 值大小 | 模型复杂度 | 偏差(Bias) | 方差(Variance) | 过拟合风险 |
|---|---|---|---|---|
| 小(如1、3) | 高(更灵活) | 低 | 高 | 高 |
| 大(如15、30) | 低(更平滑) | 高 | 低 | 低 |
因此,在实际应用中,我们不能简单追求低偏差或低方差,而是要在二者之间取得最佳平衡,以获得更好的泛化能力。
四、如何选择合适的 K 值?
以下是一些实战中的建议:
-
使用交叉验证(Cross Validation):最常见的方法是使用 K 折交叉验证,从多个候选 K 值中选出在验证集上效果最好的那个。
-
常用范围:通常,K 值选择在 3~30 之间。K=1 往往过拟合,而 K 太大可能导致欠拟合。
-
奇数优先:在分类任务中,优先选择奇数可以避免投票结果出现平局。
-
考虑样本大小:样本数较小时,K 不宜太大,以免失去个体差异性;数据量大时,可以适当增大 K 值提升稳定性。
-
考虑维度问题:在高维空间中,距离度量不再可靠(即“维度灾难”),可以考虑降维或使用加权 KNN。
五、KNN 应用场景
KNN 算法虽然简单,但在以下场景中仍然具有良好表现:
-
图像识别与搜索(如手写数字识别)
-
文本分类(如垃圾邮件识别)
-
推荐系统(基于相似用户或物品)
-
医学诊断辅助(如根据相似病例做出预测)
六、总结
K 值的选择是 KNN 算法中至关重要的一步,直接影响模型的学习能力和泛化性能。小 K 值强调个体差异,容易过拟合;大 K 值强调整体趋势,容易欠拟合。理解并掌握这种偏差-方差的权衡机制,能够让你更灵活地应用 KNN 模型于实际任务中。
希望本文的图文解析对你有所帮助。如果你喜欢这种“图解 + 技术”的方式,欢迎点赞、收藏、关注我,一起深入学习机器学习的各个知识点!
