当前位置：首页 > news >正文

排序复习/下（C语言版）

news 来源：原创 2025/5/20 7:28:27

1.快速排序（hoare法）

单趟：

整体：

代码优化：

编辑三数取中代码：

小区间优化代码：

hoare法疑问解答：

2.快速排序（挖坑法）

3.快速排序（前后指针法）

性能分析：

全部代码（递归版）：

4.快速排序（非递归）

5.归并排序

性能分析：

6.归并排序（非递归）

全部代码：

7.计数排序（非比较排序）

性能分析：

8.排序稳定性

1.快速排序（hoare法）

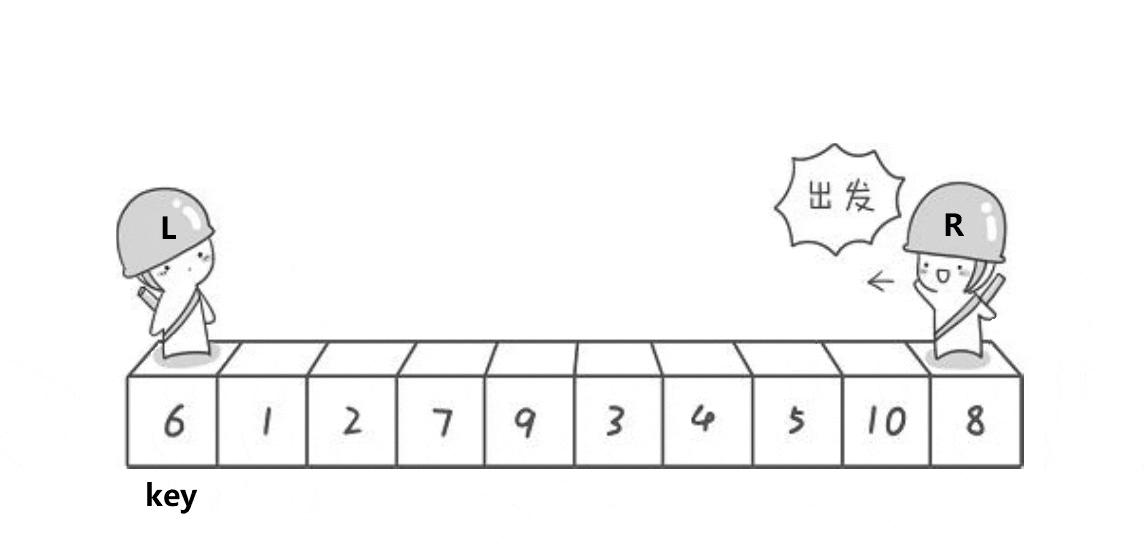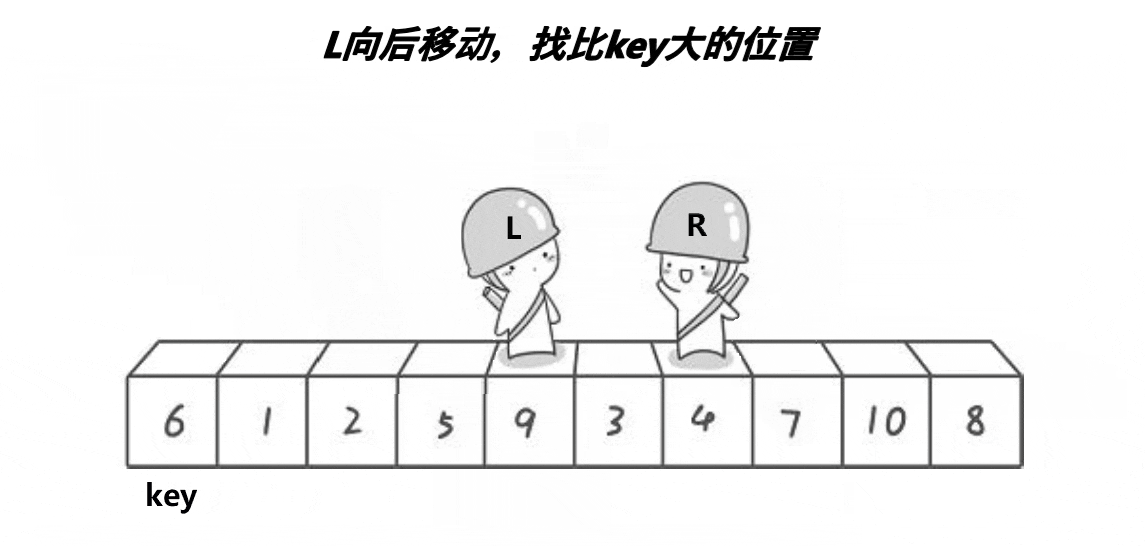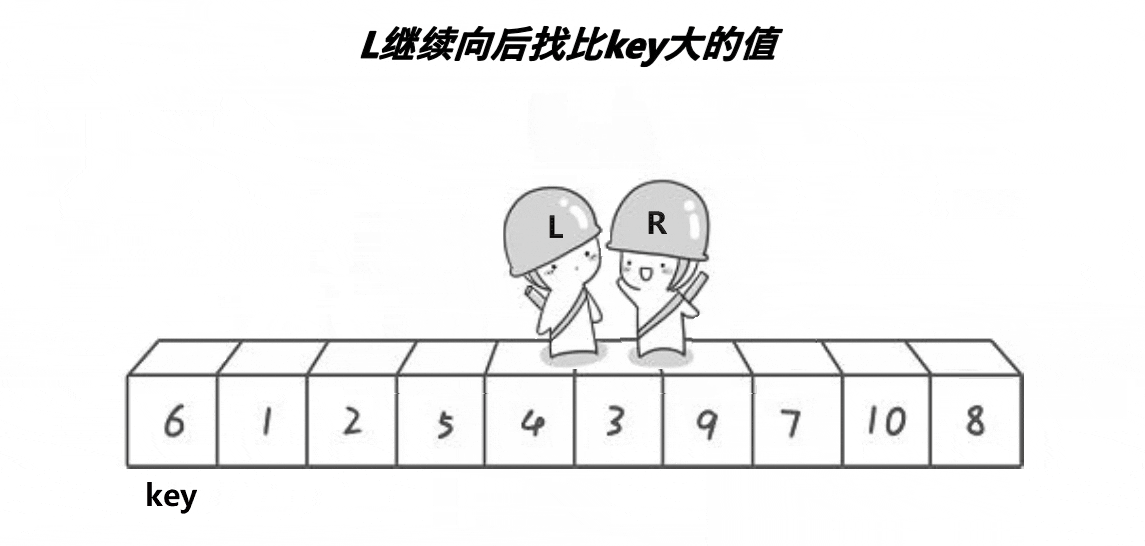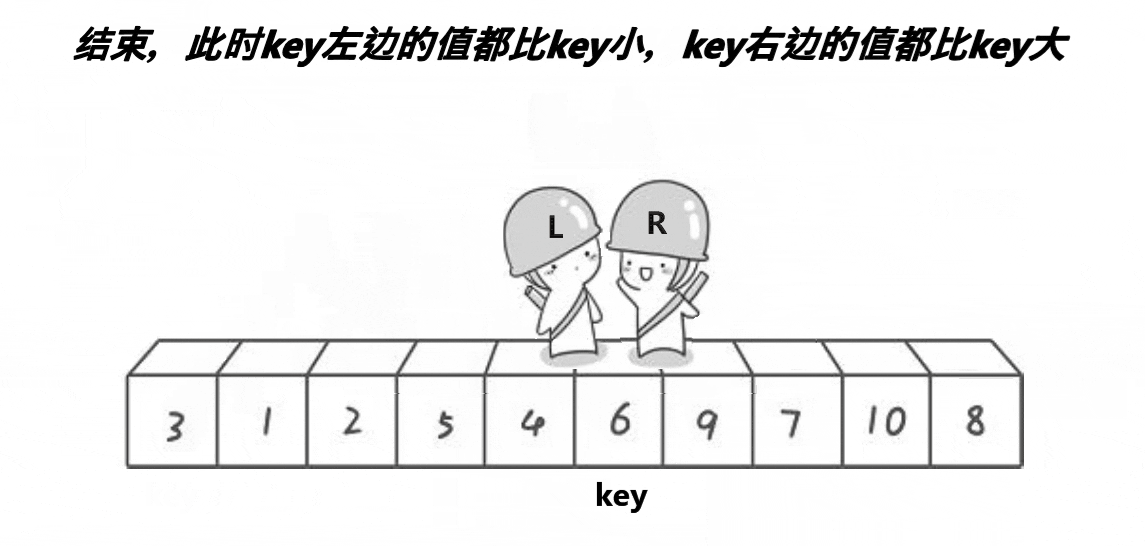
单趟：

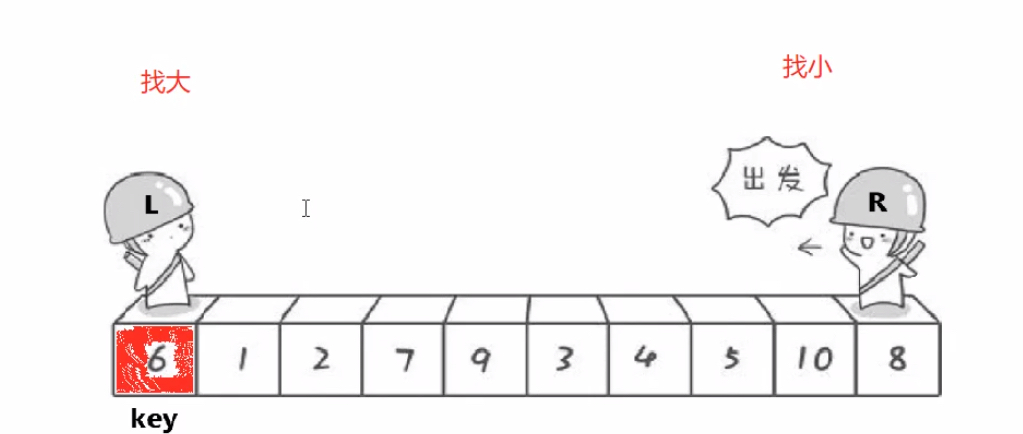
   （一般）以第一个值为key，通过一系列操作让比它大的值全在其右边，比它小的都在左边
   操作方法：定义两个指针left、right，left找大right找小，当找到了2个值以后，交换两个位置的元素；这样操作到left、right相遇，然后把begin位置的key值和left位置的元素交换
   此时key值已经排序完成了，因为其左边都是较小值，右边都是较大值

	int left = begin, right = end;int keyi = begin;while (left < right)//相等时结束循环{while (left < right && a[right] >= a[keyi])right--;//left不能大于rightwhile (left < right && a[left] <= a[keyi]) left++;//必须要先走右指针，再走左指针Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);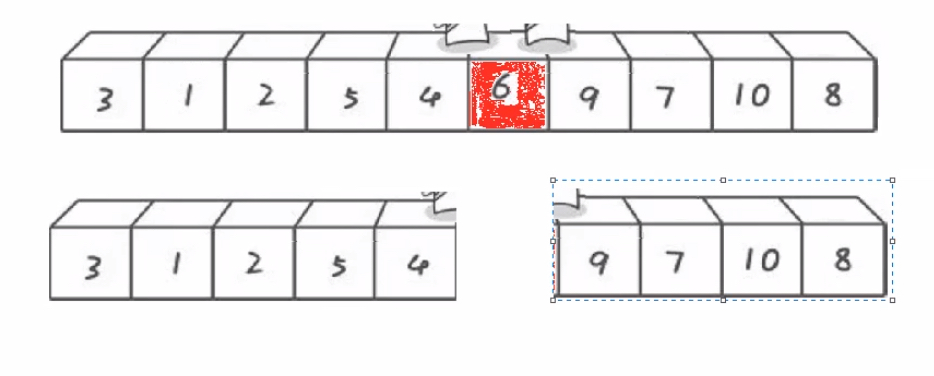

整体：

因为key已经排序完了，所以只需要对key的左右区间分别排序即可；对其左右区间分别再次进行快排，一整个问题可以由无数个子问题组成，不难想到使用递归实现
递归出口：begin >= end
如图，此时上一步是 begin = 0，end = 1，left(keyi) = 1；进入到递归调用函数以后，往左递归是(a,0,0) -> 一个单值，往右递归是(a,2,1) -> 不存在值

void QuickSort(int* a, int begin, int end)
{	if (begin >= end) return;int left = begin, right = end;int keyi = begin;while (left < right)//相等时结束循环{while (left < right && a[right] >= a[keyi])right--;//left不能大于rightwhile (left < right && a[left] <= a[keyi]) left++;//必须要先走右指针，再走左指针Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);QuickSort(a, begin, left - 1);QuickSort(a, left + 1, end);
}

代码优化：

   优化1：三数取中
   如上图，对于有序的数组，key值永远都取整个区间的最开头一个；（如果是升序）right会直接往左移动到key值位置，因此第一次的循环为N次；
   接下来左区间没有东西，往右区间走，又是以开头值为key值，循环N-1次；然后左边区间没有东西（区间begin = 1 ，此处不是看数组来判断的），右边区间又是以开头值为key值……
   整体时间复杂度会达到惊人的"N + (N - 1) + …… + 2 + 1 = O(N^2) ,
   同时因为每次函数递归调用都需要开辟一个函数栈帧，N个数据的有序数组就得开辟N个栈帧；debug版本（栈帧带着调试信息）下，100000个栈帧就会栈溢出
   因此我们可以通过在begin end mid 三个位置中找中间大小的数据，把他作为key值来解决这个问题（数组有序时，key值作为中间大小，能够左右区间都有数据去快排）

     优化2：小区间优化
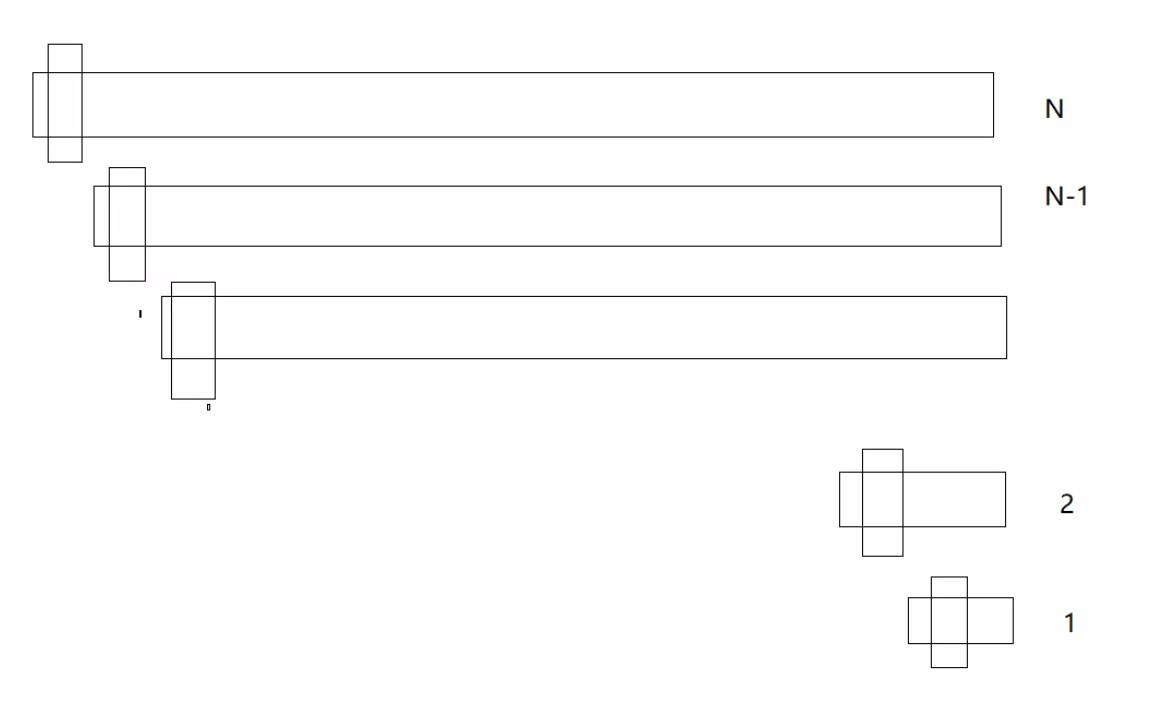
   假设每次对某一个区间快速排序完，key都落在了中间位置，那我们可以把函数递归调用看作是一棵完全二叉树在进行先序遍历（当中key值为父节点，左右区间为父节点的左右子树）
   如下图，根据完全二叉树的特点，最后一层根节点占到了所有节点的50%，倒数第二层占了25%；由于倒数几层的递归调用开销很大，因此最后几层我们可以不使用快速排序，改用别的排序方法
   希尔排序主要用来排大量数据，冒泡快速太拉了，堆排还需要创建堆然后才能排序（每个区间都要创建堆，时间开销比较大），归并排序也得要递归调用，所以插入排序是最好的选择（c++sort函数用的就是插入排序+快排）

三数取中代码：

int GetMid(int* a, int left, int right)
{int midi = (right - left) / 2;if (a[left] < a[midi]){if (a[midi] < a[right]) return midi;else if (a[left] < a[right]) return right;else return left;}else //a[left] > a[midi]{if (a[midi] > a[right]) return midi;else if (a[left] < a[right]) return left;else return right;}
}void QuickSort(int* a, int begin, int end)
{    ……;int midi = GetMid(a, begin, end);Swap(&a[begin], &a[midi]); //key值一定要放在最开头/最末尾的位置……;
}

小区间优化代码：

    if ((end - begin + 1) <= 10) InsertSort(a + begin, end - begin + 1);

只要递归到某一个区间，区间内数据量小于等于10，就停止快排使用插入排序
如果传参传的是a+4，那么在InsertSort函数里，a[0]（函数里逻辑上的数组） = a[4]（实际存储空间里的数组）

hoare法疑问解答：

   疑问1：为什么key值一定要放在区间头/尾？
   如果key放在中间位置，前面有值，那么有可能left、right在key值前面相遇，本来应该放在key值左边的元素现在放到key值右边了，肯定会出问题

   疑问2：为什么key放在区间头，一定要右指针先移动呢？
   key值由于放在头部，因此在左右指针相遇后，相遇位置处的值需要小于key值，这样才能保证key左边都是比它小的，右边都是比它大的
   右指针是专门去找小的指针，一般性会有以下3种情况：
   1.right找到小的以后，left不断找大，一直没找到直到和right相遇 -> 相遇位置值比key小
   2.left、right位置的值已经交换过数对，right不断找小一直没找到，与left相遇后由于前一次left、right（新一次找小开始的位置）的交换，当前left所指向的值依旧小于key值
   3.left一次也没动过，right不断找小，一直没找到直到与left相遇，此时相当于key和key自己进行了一次位置交换
   记忆方法：左边key右边先走，右边key左边先走

2.快速排序（挖坑法）

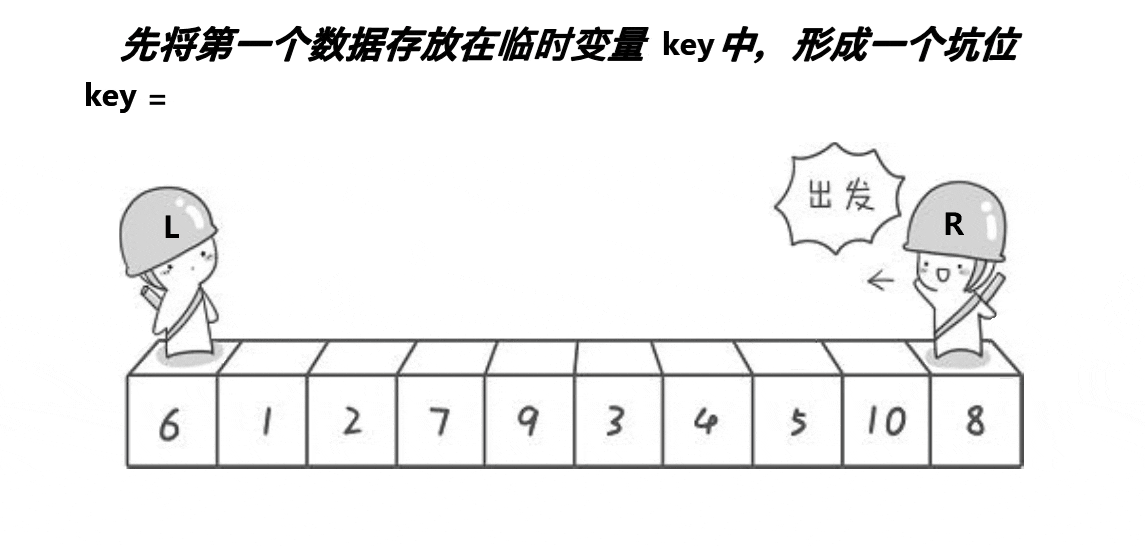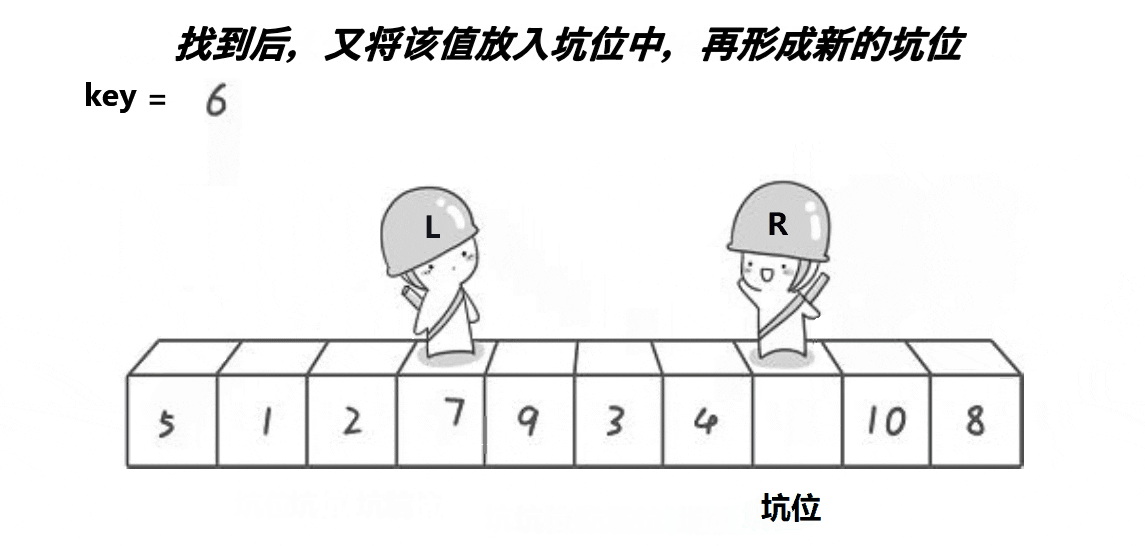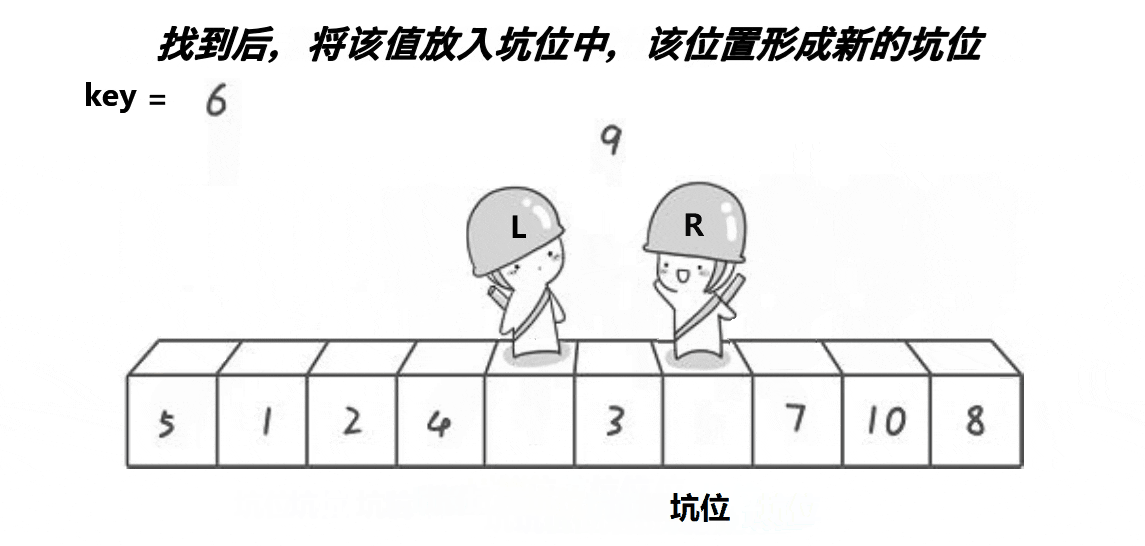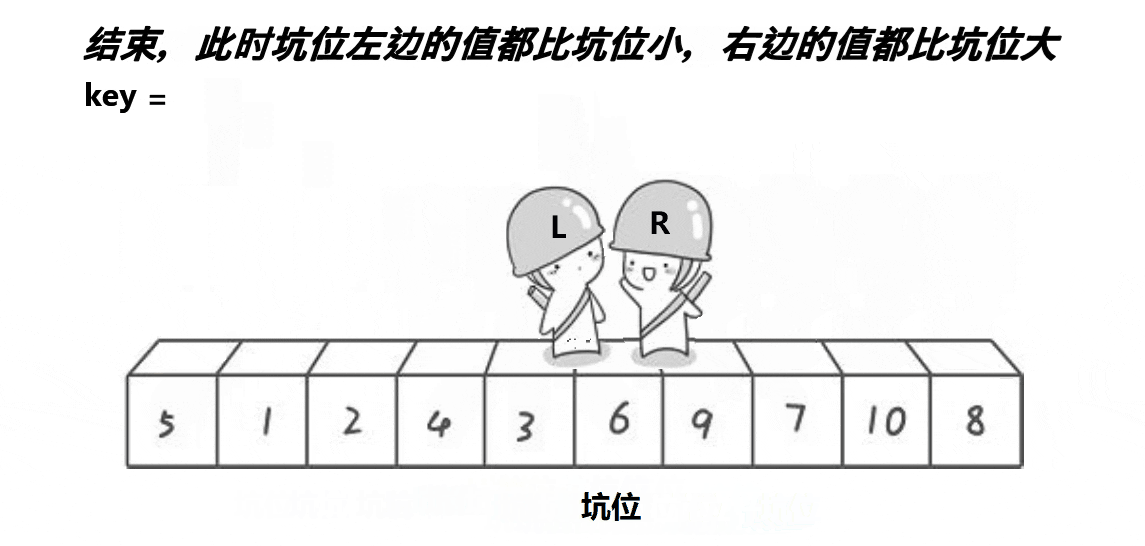
没有效率提升，但很多hoare法带来的疑问不需要分析了，因此比较好理解

3.快速排序（前后指针法）

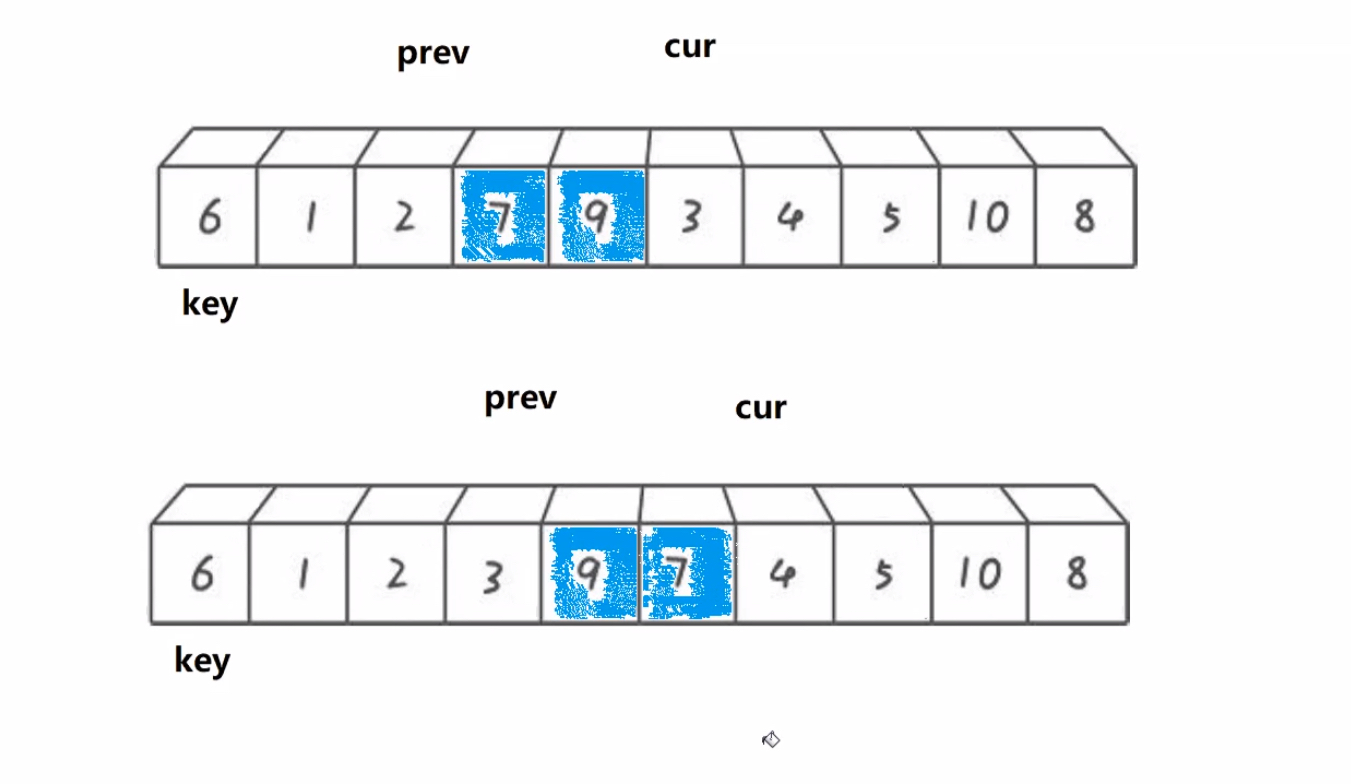
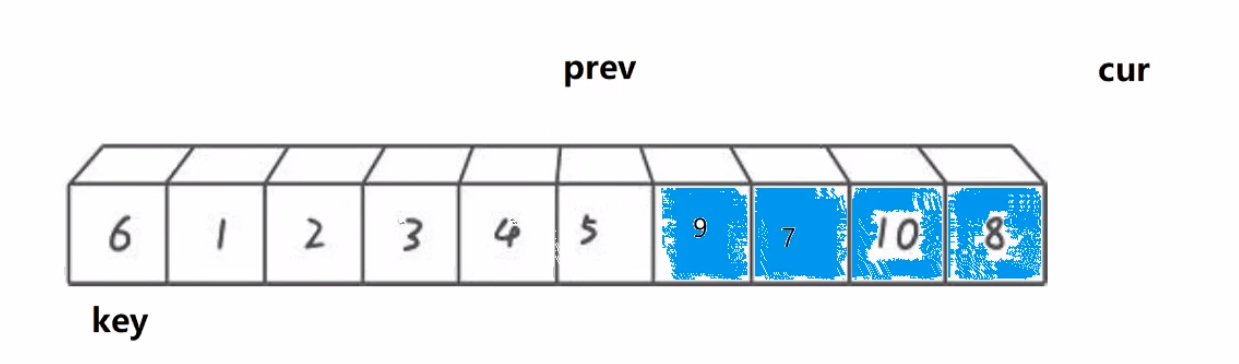
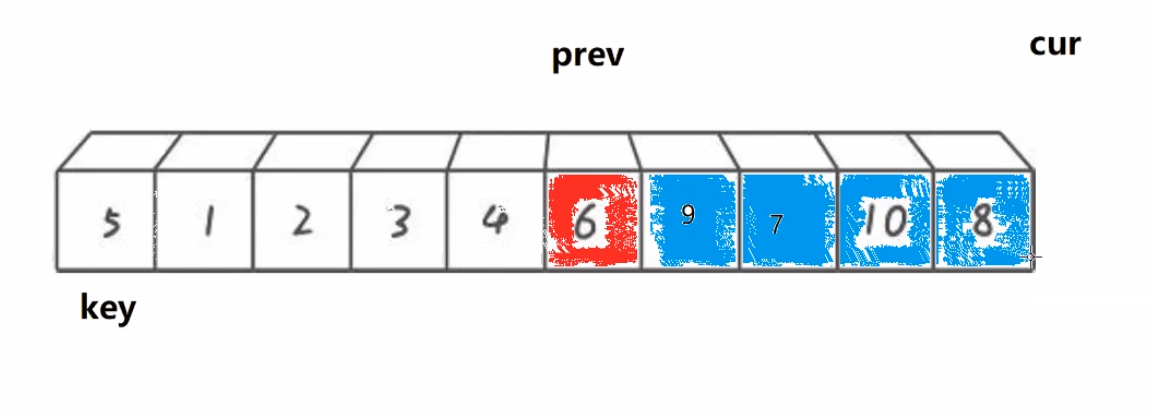
   1.搞一个prev指针，再搞一个cur指针，初始都在begin位置
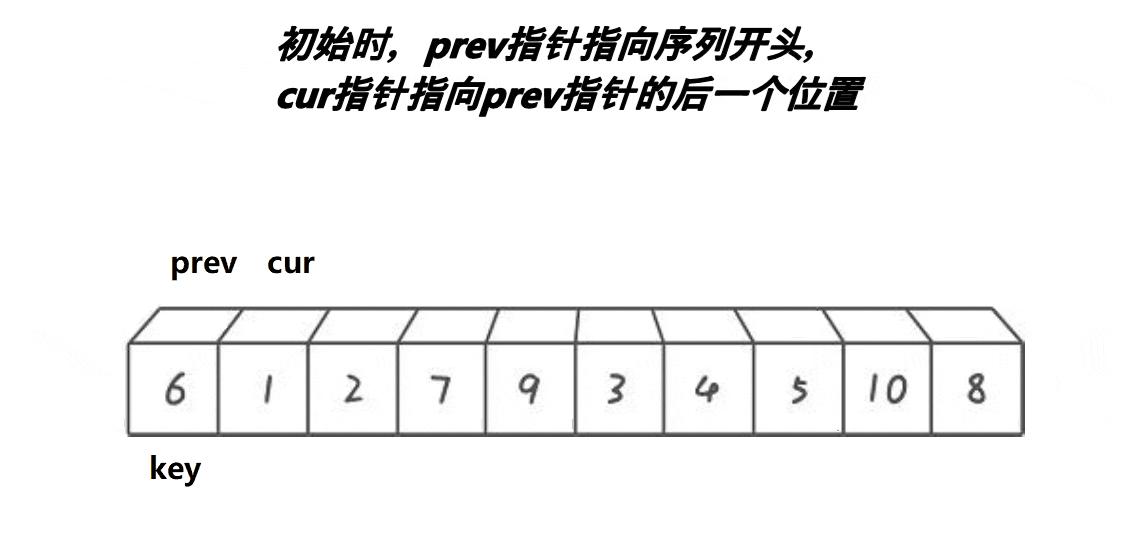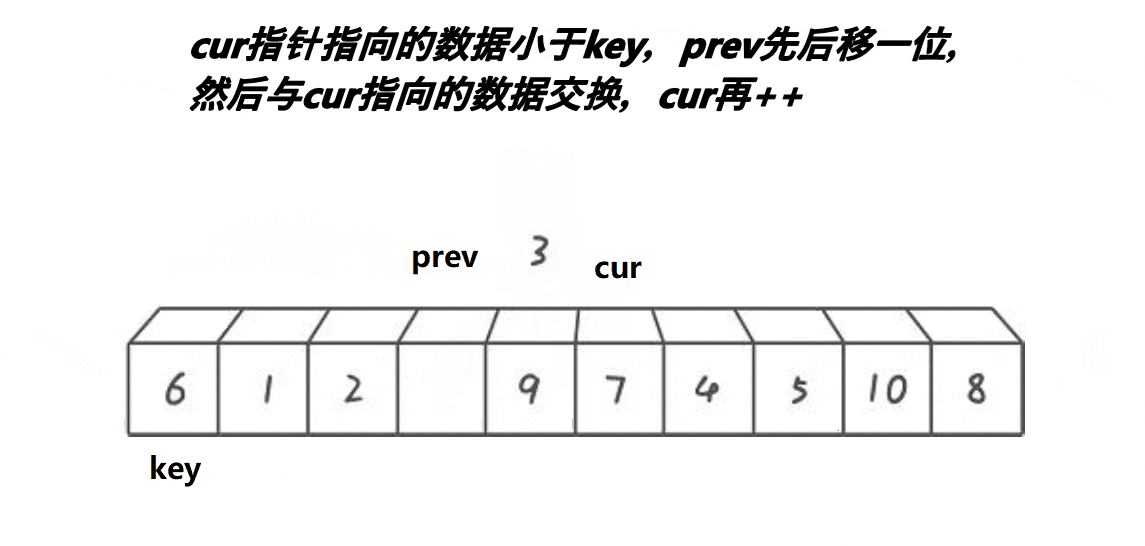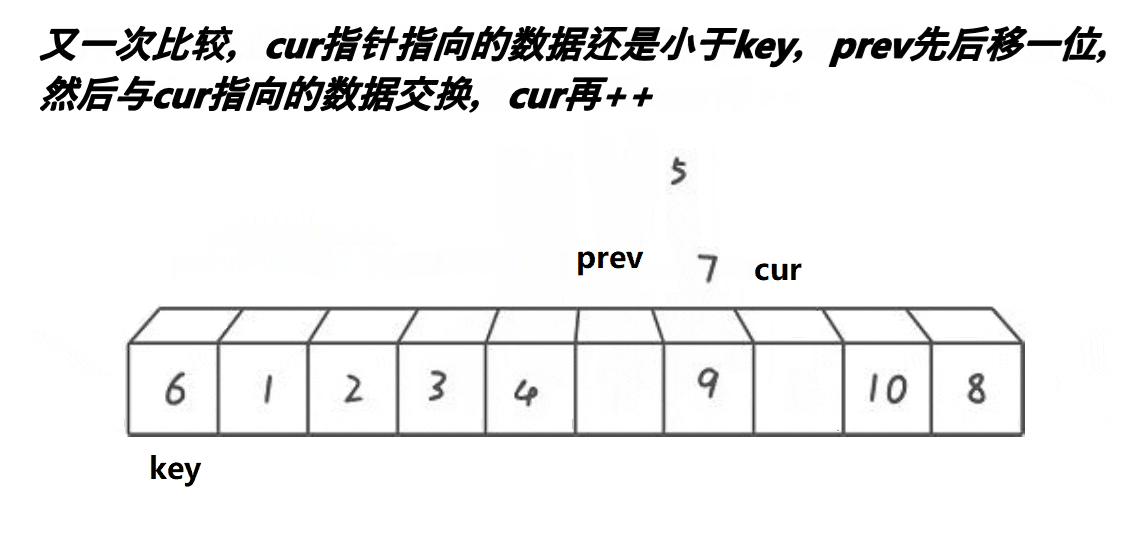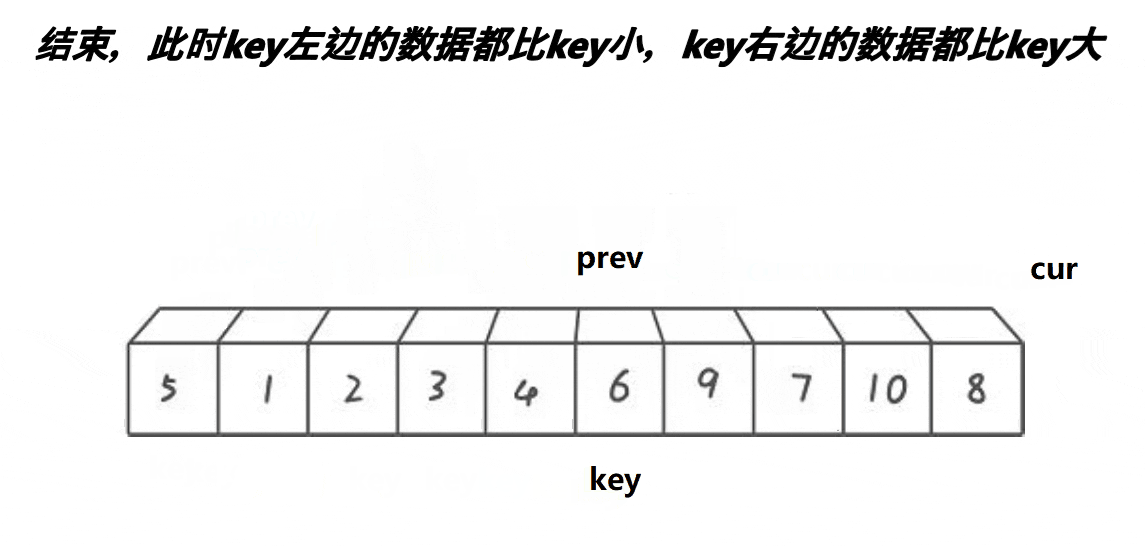
   2.cur找大（比key大），cur和prev同步向后走，直到cur找到大
   3.cur从找大变成找小，大的cur往后走prev不动(由于每次肯定cur先走，所以prev的限制是比较容易的），找到小的让prev先++，然后进行位置交换，此时就类似于把大于key的值翻滚往后移动
   4.cur遍历完数组，交换prev和keyi位置元素
   如果初始化时cur = begin + 1，那么就用后置++特性，自己和自己交换也可以

	int prev = begin, cur = begin ;int keyi = begin;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur) Swap(&a[prev], &a[cur]);cur++;}Swap(&a[prev], &a[keyi]);

性能分析：

时间复杂度：O(NlogN)，总共有logN层，每层需要遍历N个数
空间复杂度：O(logN)，需要开辟logN个栈帧

全部代码（递归版）：

int PartSort1(int* a, int begin, int end)
{int left = begin, right = end;int keyi = begin;while (left < right)//相等时结束循环{while (left < right && a[right] >= a[keyi])right--;//left不能大于rightwhile (left < right && a[left] <= a[keyi]) left++;//必须要先走右指针，再走左指针Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);return left;
}int PartSort2(int* a, int begin, int end)
{int prev = begin, cur = begin ;int keyi = begin;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur) Swap(&a[prev], &a[cur]);cur++;}Swap(&a[prev], &a[keyi]);return prev;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end) return;int midi = GetMid(a, begin, end);Swap(&a[begin], &a[midi]); //key值一定要放在最开头/最末尾的位置if ((end - begin + 1) <= 10) InsertSort(a + begin, end - begin + 1);//hoare法int left = PartSort1(a, begin, end);//前后指针法//int left = PartSort2(a, begin, end);QuickSort(a, begin, left - 1);QuickSort(a, left + 1, end);}

4.快速排序（非递归）

   非递归一般使用栈or队列来完成
   每次递归最重要的就是区间的起始下标与终止下标
   所以我们可以：循环没走一次，取栈顶空间，单趟排序然后左右子区间的起止下标入栈

[begin, keyi-1] keyi [keyi+1, end] 左右区间后进先出，所以begin如果要先出就得插入时后插入

typedef struct Stack
{int* a; //动态开辟int top; //栈顶int capacity; //可容纳空间
}st;void Stinit(st* pst)
{assert(pst);pst->a = NULL;pst->capacity = 0;pst->top = -1;
}
void Stdestory(st* pst)
{assert(pst);free(pst->a);pst->a = NULL;pst->capacity = 0;pst->top = -1;
}
void Stpush(st* pst, int x)
{assert(pst);//扩容if (pst->top + 1 == pst->capacity){int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;int* tmp = (int*)realloc(pst->a, sizeof(int) * newcapacity);if (tmp == NULL){perror("realloc fail");return;}pst->a = tmp;pst->capacity = newcapacity;}pst->a[++pst->top] = x;
}
void Stpop(st* pst) //用函数进行封装，易于管理与理解
{assert(pst);pst->top--;
}
int Sttop(st* pst)
{assert(pst);assert(pst->top >= 0);return pst->a[pst->top];
}
bool Stempty(st* pst)
{assert(pst);return pst->top == -1;
}
int Stsize(st* pst)
{assert(pst);return ++pst->top;
}void QuickSortNON(int* a, int begin, int end)//非递归写法
{st s;Stinit(&s);Stpush(&s, end);Stpush(&s, begin);while (!Stempty(&s)){int left = Sttop(&s);Stpop(&s);int right = Sttop(&s);Stpop(&s);//区间下标的获取int keyi = PartSort2(a, left, right);// [begin, keyi-1] keyi [keyi+1, end]if (keyi + 1 < right)//放入右区间的起止下标{Stpush(&s, right);Stpush(&s, keyi + 1);}if (left < keyi - 1)//放入左区间的起止下标{Stpush(&s, keyi - 1);Stpush(&s, left);}}
}

非递归就是从dfs变成了bfs
因为非递归不需要创建函数栈帧，所以没有栈溢出风险；同时栈、队列这类数据结构，空间开辟在堆区，在4G内存中堆区大小为2GB，因此空间大小可以支持更多的数据进行排序

5.归并排序

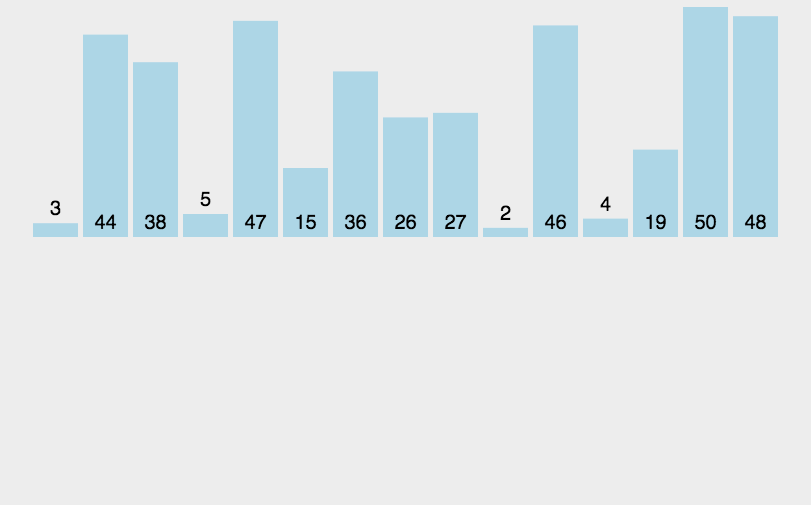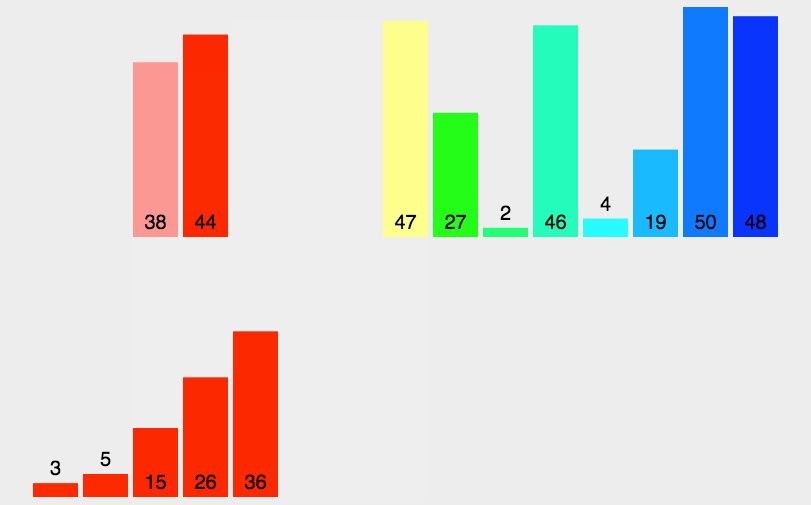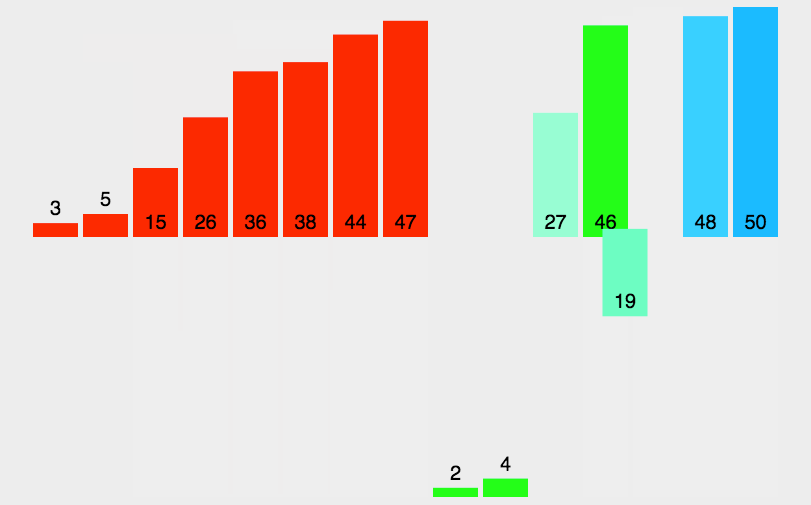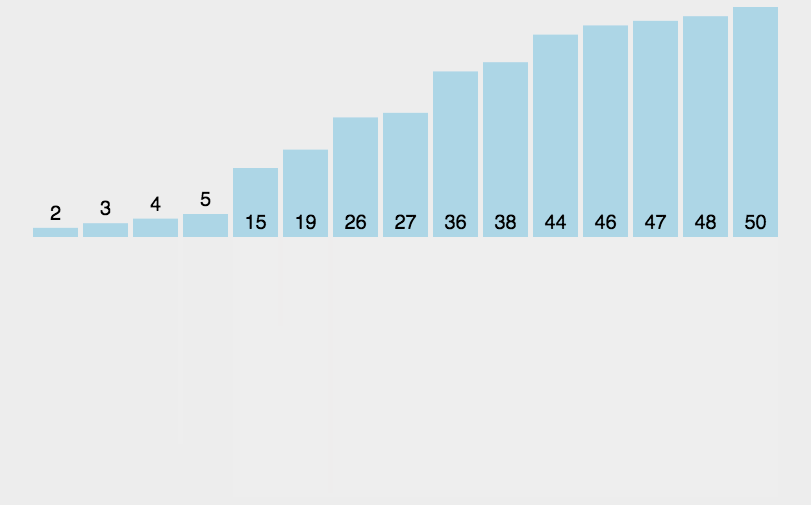
   1.把数组平分成两块，然后对两块分别再平分
   2.分到不可再分，开始归
   3.归时进行小区间的排序，小区间合并成大区间以后，再对大区间进行排序，以此类推……
   4.需要创建一个temp数组进行排序（例如2个数的区间，小的先放进temp，再放大的，自然排序完成了；大的区间，因为左右区间都有序了，所以比较放入temp时也是比较容易的）
   5.平分成一个个小区间可以通过递归来实现（子问题是大区间平分成小区间，然后归并成大区间）

void _MergeSort(int* a, int* temp, int begin, int end)
{//分->exit//递归出口理由同快排if (begin >= end) return;//分->initint midi = (begin + end) / 2;//二分//分->r&t_MergeSort(a, temp, begin, midi);_MergeSort(a, temp, midi+1, end);//归并+排序int begin1 = begin, end1 = midi;//左区间int begin2 = midi + 1, end2 = end;//右区间int i = 0;//temp数组下标从0开始while (begin1 <= end1 && begin2 <= end2)//左右区间都还有值，直到一个没有值推出循环{if (a[begin1] < a[begin2]) temp[i++] = a[begin1++];else temp[i++] = a[begin2++];}while (begin1 <= end1) temp[i++] = a[begin1++];while (begin2 <= end2) temp[i++] = a[begin2++];memcpy(a + begin, temp, (end - begin + 1) * sizeof(int));
}void MergeSort(int* a, int n)
{int* temp = (int*)malloc(n * sizeof(int));if (!temp){perror("malloc error");return;}_MergeSort(a, temp, 0, n - 1);free(temp);temp = NULL;
}

代码重点解释：

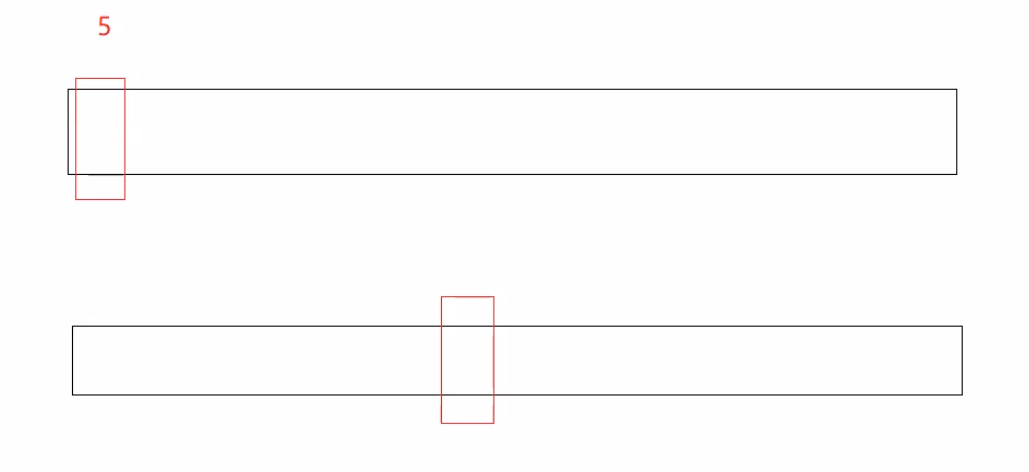
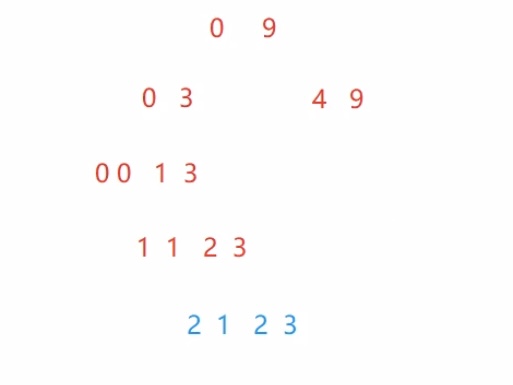
    [begin,midi-1][midi,end]这样来区间划分会导致死循环（如下图1）
   最后一层{2,3}的右区间会不断形成{2,3}，a[midi] = 2 a[end] = 3

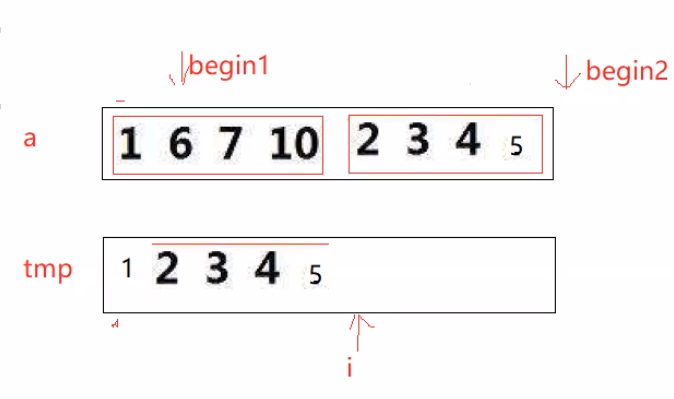
   while (begin1 <= end1) temp[i++] = a[begin1++];
   while (begin2 <= end2) temp[i++] = a[begin2++];

根据循环退出条件，此时肯定还有一个区间有值，把剩下来没有放进（具体如下图2）

memcpy(a + begin, temp, (end - begin + 1) * sizeof(int));

将结果放入原数组（原数组需要从begin下标处开始覆盖，temp每次新值会覆盖旧值，所以可以多次使用）

性能分析：

   时间复杂度：N*logN
   某一层假设有4个小区间，每个小区间都遍历一遍相当于数组遍历了一边，时间复杂度为 N
   递归看成完全二叉树，总共是进行了 logN 次区间遍历，因此时间复杂度为nlogn
   空间复杂度：N

   归并排序是一种外排序
   假设只有1G内存，把4G的大文件拆分成4个1G的小文件，对4个小文件分别进行排序（用更快的，例如希尔）
   然后再对4个小文件使用归并排序，归并成一个大文件，4G的数据就有序了
   能够通过小内存来处理大数据的，我们一般称为外排序（可以理解成用内存来完成磁盘的活）

6.归并排序（非递归）

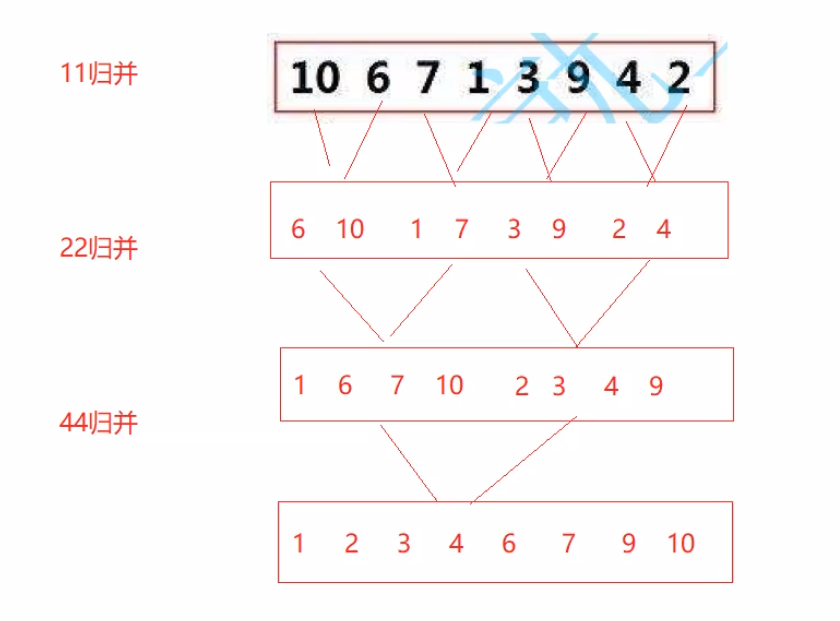
   归并的递归不使用栈和队列这类数据结构
   快排是操作+左右递归 -> 先序遍历
   归并是左右递归+操作 -> 后序遍历
   难以通过栈来实现后序遍历，因为后序遍历就决定了得先把下标依次全都放进栈，然后才能操作，使用栈无法实现归并的操作
   因此我们可以使用希尔排序的思想，将数据之间看作是多个区间对，例如4个数的数组： [0,1][2,3] -> [0,0][1,1] [2.2][3.3] 从右往左，先是两个数一块排，再是4个数一块排
   因此我们可以用到gap作为区间值的距离
   [i,i+gap-1][i+gap,i+2*gap-1] 数组下标从0开始算，所以区间终止位置下标需要-1
   其余思想与递归实现相同

void MergeSortNON(int* a, int n)
{int* temp = (int*)malloc(n * sizeof(int));if (!temp){perror("malloc error");return;}int gap = 1;while (gap < n){for (int i = 0;i < n;i += 2 * gap){int begin1 = i, end1 = i + gap - 1;//左区间int begin2 = i + gap, end2 = i + 2 * gap - 1;//右区间int j = 0;//temp数组下标从0开始while (begin1 <= end1 && begin2 <= end2)//左右区间都还有值，直到一个没有值推出循环{if (a[begin1] < a[begin2]) temp[j++] = a[begin1++];else temp[j++] = a[begin2++];}while (begin1 <= end1) temp[j++] = a[begin1++];while (begin2 <= end2) temp[j++] = a[begin2++];memcpy(a + i, temp, (end2 - i + 1) * sizeof(int));//这边i不能用begin，begin已经被修改掉了}gap *= 2;}free(temp);temp = NULL;
}

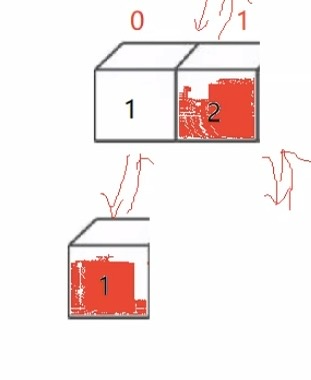
当数组的数据不是2的倍数时，有可能会导致数组越界，以下是数组越界的三种情况：

假设有一个有10个数据的数组，归并排序时会出现以下几个越界：

如上图所示，对应了错误2、错误3 [8,9][10,11] & [8,11][12,15]
此时，因为[8,9]区间的值通过前一步的操作已经有序了，所以可以直接结束本次循环（即不用归并）；只有begin1没有越界or第二组越界，end1越界begin2必越界，所以可以放在一个判断语句里判断 -> 不需要归并了，用break就好不用continue，因为越界肯定发生在最后一组区间对上

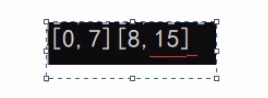
如上图所示，对应了错误1
此时[0,7][8,9]需要进行归并，所以我们可以手动将 end2 赋为 n-1

全部代码：

void MergeSortNON(int* a, int n)
{int* temp = (int*)malloc(n * sizeof(int));if (!temp){perror("malloc error");return;}int gap = 1;while (gap < n){for (int i = 0;i < n;i += 2 * gap){int begin1 = i, end1 = i + gap - 1;//左区间int begin2 = i + gap, end2 = i + 2 * gap - 1;//右区间if (begin2 >= n) break;if (end2 >= n) end2 = n - 1;int j = 0;//temp数组下标从0开始while (begin1 <= end1 && begin2 <= end2)//左右区间都还有值，直到一个没有值推出循环{if (a[begin1] < a[begin2]) temp[j++] = a[begin1++];else temp[j++] = a[begin2++];}//根据循环退出条件，此时肯定还有一个区间有值；把剩下来没有放进（图）while (begin1 <= end1) temp[j++] = a[begin1++];while (begin2 <= end2) temp[j++] = a[begin2++];memcpy(a + i, temp, (end2 - i + 1) * sizeof(int));//这边i不能用begin，begin已经被修改掉了}gap *= 2;}free(temp);temp = NULL;
}

7.计数排序（非比较排序）

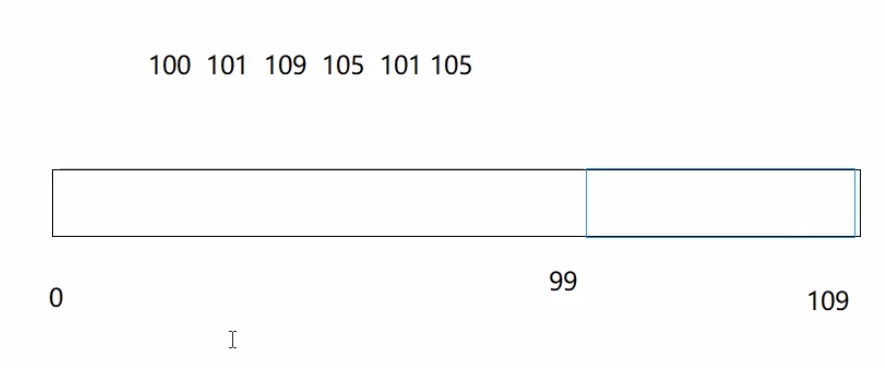
   1.搞一个count数组
   2.count数组下标对应的就是原数组中某一个元素，count数组某个下标所对应的元素大小即原数组中某一元素个数
   3.原数组里的值都比较大的话，可以通过 count[a[i]-min] 来优化 min为原数组中的最小元素（图）
   4. 3 9 100 105 这个数组依旧可以完成排序，min = 3 max = 105 range = 102，105->[102] 100->[97] 9->[6] 3->[0]
   5.负数range范围能概括到，并且i+min可以减到负数，因此负数也可以用该办法进行排序

void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (int i = 1;i < n;i++){if (a[i] < min) min = a[i];if (a[i] > max) max = a[i];}int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));if (!count){perror("calloc error");return;}//统计出现次数for (int i = 0;i < n;i++) count[a[i] - min]++;//放到原数组里int j = 0;for (int i = 0;i < range;i++){while (count[i]--) a[j++] = i + min;}free(count);count = NULL;
}

calloc(range, sizeof(int))是带初始化的malloc，相当于malloc + memset(count, 0, range * sizeof(int))

性能分析：

时间复杂度：range + N （range是对count数组遍历，原数组N个数，因此还需要 +N ）
空间复杂度：range
只适合整数/数据范围比较集中（相当于用空间换时间）

8.排序稳定性

稳定性关注的是相同值排序以后，相同值的相对顺序是否有发生变化
例如上图的2个5，红前蓝后经过多次排序以后，依然还是红前蓝后，说明是稳定的

为什么需要去判断稳定性呢？
在实践时，一般都是对结构体进行排序；假设有张三、李四两个人的成绩结构体（两人的成绩相同），并且要求张三信息必须要在李四前面，如果不具备稳定性那么张三这条信息就放在李四后了，因此需要去考虑稳定性

插入排序：稳定（相等时不挪动，因此相对顺序没有变）
希尔排序：不稳定（分组不同导致的）
选择排序：不稳定（6 6 1 1 9 7 ，min = 1 begin=0 ,a[0] 和 a[2] 交换位置以后，放在数组首部的元素6失去了稳定性）
冒泡排序：稳定（相等时不交换位置）
快速排序：不稳定（只要left、right下标2值交换位置，就有可能打破原有的相对顺序）
归并排序：稳定（相同值在不同区间，通过a[begin1]<=a[begin2]把a[begin1]放进temp数组即可保证稳定；相同值在相同区间，是通过前面归并的操作到了当前这一步的，肯定稳定）

堆排序：不稳定（相同值在不同子树，向上调整建堆时会破坏相对顺序）