【从基础到模型网络】深度学习-语义分割-基础
语义分割在深度学习与人工智能领域占据重要地位。它是计算机视觉的核心任务之一,能够将图像像素级地划分为不同语义类别,为理解图像内容提供关键支持。在自动驾驶中,可精准识别道路、车辆、行人等元素,保障行车安全;在医学影像分析中,能准确分割器官和病变区域,辅助疾病诊断。此外,它还广泛应用于机器人视觉、卫星图像分析等领域,推动人工智能向更精准、更智能的方向发展,是实现智能视觉感知的关键技术。
目录
上采样
双线性插值
转置卷积
上采样
上采样(upsampling)一般包括2种方式:
- Resize,如双线性插值直接缩放,类似于图像缩放(这种方法在原文中提到)
- Deconvolution,也叫Transposed Convolution
双线性插值
线性插值

双线性插值
又称为双线性内插。在数学上,双线性插值是有两个变量的插值函数的线性插值扩展, 其核心思想是在两个方向分别进行一次线性插值。
如图,已知Q12,Q22,Q11,Q21,但是要插值的点为P点,这就要用双线性插值 了,首先在x轴方向上,对R1和R2两个点进行插值,这个很简单,然后根据R1和R2对 P 点进行插值,这就是所谓的双线性插值。在数学上,双线性插值是有两个变量的插值函数 的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值。
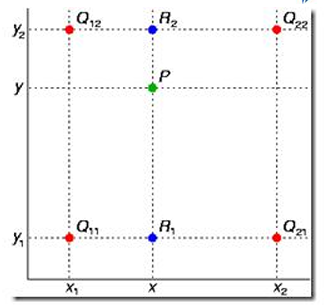
假如我们想得到未知函数 f 在点 P = (x, y) 的值,假设我们已知函数 f 在 Q11 = (x1,
y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值。
首先在 x 方向进行线性插值,得到

然后在 y 方向进行线性插值,得到
![]()
这样就得到所要的结果 f(x, y),

如果选择一个坐标系统使得 f 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1,
1),那么插值公式就可以化简为
![]()
或者用矩阵运算表示为

重点放在最后得到的矩阵的理解
双线性插值可以理解为 “两步走” 的加权估算,就像在一张方格纸上,通过四个角的已知值,估算中间某点的值。



转置卷积
conv2d_transpose(
x,
filter,
output_shape,
strides,
padding='SAME',
data_format='NHWC',
name=None
)
参数解释
filter: [kernel_size,kernel_size, output_channels, input_channels] 这里的转置卷积核
和正向卷积核有区别,在于通道数参数的放置位置,因为转置卷积是正向卷积的逆过程,所
以放置的位置相反。
实现过程
(其实就是将输入扩充后进行卷积)
先填充后卷积,本质和普通卷积没设么区别

Step 1 扩充
将 inputs 进行填充扩大,扩大的倍数与 strides 有关(strides 倍)。扩大的方式是在
元素之间插[ strides - 1 ]个 0。padding="VALID"时,在插完值后继续在周围填充的宽度
为[ kenel_size - 1 ],填充值为 0;padding = "SAME"时,在插完值后根据 output 尺寸进行填充,填充值为 0。
Step 2 卷积
对扩充变大的矩阵,用大小为 kernel_size 卷积核做卷积操作,这样的卷积核有 filters
个,并且这里的步长为 1(与参数 strides 无关,一定是 1)
注意:
conv2d_transpose 会计算 output_shape 能否通过给定的 filter,strides,padding 计算
出 inputs 的维度,如果不能,则报错。也就是说,conv2d_transpose 中的filter,strides,padding 参数,与反过程中的 conv2d 的参数相同。
转置卷积的直观解释
转置卷积(也叫反卷积)的本质是卷积的 “反向操作”,但不是严格意义上的逆运算。它通过插入空格(Zero Padding)和标准卷积来实现特征图的上采样。
Step 1: 扩充(Insert Zeros & Padding)
按 Strides 倍数插入空格
假设输入是一个 2×2 的矩阵,strides=2:
输入 (2×2)
[[1, 2],[3, 4]
]
插入空格后 (4×4)
[[1, 0, 2, 0],[0, 0, 0, 0],[3, 0, 4, 0],[0, 0, 0, 0]
]
规律:在每个元素之间插入 strides-1 个零(这里是 2-1=1 个零),使矩阵尺寸变为原来的 strides 倍。
按 Padding 规则补零
假设卷积核大小 kernel_size=3×3:
padding="VALID":在矩阵周围填充 kernel_size-1 圈零(这里是 3-1=2 圈):plaintext
填充后 (8×8):
[[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 1, 0, 2, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 3, 0, 4, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0]
]
padding="SAME":根据输出尺寸动态计算填充量,确保输出尺寸符合预期(通常使输出与输入尺寸成 strides 倍关系)。
Step 2: 卷积(标准卷积操作)
使用 3×3 卷积核对扩充后的矩阵进行卷积,步长固定为 1:
卷积核 (3×3)
[[a, b, c],[d, e, f],[g, h, i]
]
卷积过程:卷积核在扩充后的矩阵上滑动(步长 = 1),每次覆盖一个 3×3 区域;将卷积核与覆盖区域逐元素相乘后求和,得到输出矩阵的一个元素;重复此过程,直到覆盖整个扩充矩阵。
示例结果(简化)
假设卷积后得到一个 4×4 的输出矩阵(实际尺寸由 padding 和 kernel_size 决定):
输出 (4×4)
[[a, b+2d, c+2f, 2i],[d+3g, e+2h+3b, f+2i+3d, 2h+4f],[g+3a, h+3b+2d, i+3c+2f, 2b+4e],[3a, 3b+2d, 3c+2f, 2e+4h]
]
为什么这样设计?
尺寸关系的反向性
转置卷积的参数(filters, strides, padding)与正向卷积完全对称:
正向卷积:输入尺寸 H×W → 输出尺寸 (H+2P-K)/S+1 × (W+2P-K)/S+1。
转置卷积:输入尺寸 H×W → 输出尺寸 (H-1)×S-2P+K × (W-1)×S-2P+K。
tip:‘K’代表卷积核(kernel)的大小 。通常在二维卷积里,如果卷积核是正方形,K 指的就是卷积核的边长,比如 3×3 的卷积核,此时 K = 3 ;如果是长方形卷积核,在计算中一般也会统一按较大边长等情况处理
例如:
正向卷积:3×3 输入 → 2×2 输出(stride=2, padding=0)
转置卷积:2×2 输入 → 3×3 输出(stride=2, padding=0)
参数共享的对称性
转置卷积的卷积核与正向卷积共享相同的参数,只是计算过程相反:
正向卷积中,一个卷积核将 H×W 映射到 h×w。
转置卷积中,同一个卷积核将 h×w 映射回 H×W。
用TensorFlow框架(2.0+)的代码
import tensorflow as tf
import numpy as np# 输入:1 张图片,尺寸 28*28 高宽,通道数 3
x = np.ones((1, 28, 28, 3), dtype=np.float32)# 卷积核尺寸 4x4 ,5 表输出通道数,3 代表输入通道数
w = np.ones((4, 4, 5, 3), dtype=np.float32)# 扩大 2 倍
output = tf.nn.conv2d_transpose(
x, w, output_shape=(1, 56, 56, 5), strides=[1, 2, 2, 1], padding='SAME'
)# 直接执行,无需显式创建会话
print(output.shape)
