记录算法笔记(2025.5.17)验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
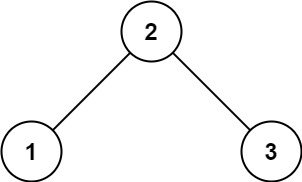
输入:root = [2,1,3]
输出:true
示例 2:
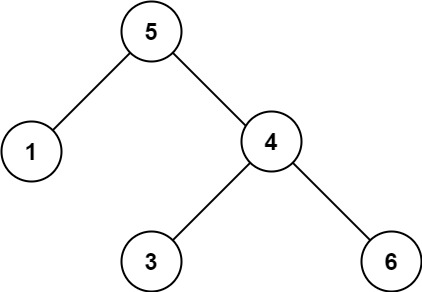
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。提示:
- 树中节点数目范围在
[1, 104]内 -231 <= Node.val <= 231 - 1
思路:
初始化
-
创建一个栈,用于存储尚未处理的节点。
-
设置一个变量
lastTreeNode,用于记录上一个访问的节点的值。初始值为long.MinValue,确保第一个节点的值总是大于它。 -
设置一个指针
current,初始指向根节点root。
主循环
循环条件是:current 不为 null 或者栈不为空。这意味着还有节点需要处理。
-
将所有左子节点压入栈:
-
从当前节点
current开始,沿着左子树一直向下,将所有左子节点依次压入栈中。 -
每次将当前节点压入栈后,将
current指向它的左子节点。 -
这一步确保了左子树的所有节点都被处理。
-
-
弹出栈顶节点并访问:
-
当左子树的所有节点都被压入栈后,弹出栈顶节点。此时,栈顶节点是当前需要访问的节点。
-
将弹出的节点赋值给
current。
-
-
检查当前节点值是否满足BST性质:
-
比较当前节点的值
current.val和上一个访问的节点值lastTreeNode。 -
如果当前节点的值小于或等于
lastTreeNode,说明这棵树不是有效的BST,直接返回false。
-
-
更新上一个访问的节点值:
-
将当前节点的值赋值给
lastTreeNode,以便在下一次循环中使用。
-
-
转向右子树:
-
将
current指向当前节点的右子节点。 -
如果当前节点没有右子节点,
current会变成null,循环会继续从栈中弹出下一个节点(即当前节点的祖先节点的右子树)。
-
循环结束
-
当
current为null且栈为空时,说明所有节点都已处理完毕。 -
如果在整个遍历过程中没有发现任何违反BST性质的情况,返回
true,表示这棵树是有效的BST。
代码:C#
public class Solution {
public bool IsValidBST(TreeNode root) {
if(root==null)
return true;
Stack<TreeNode> stack=new Stack<TreeNode>();
TreeNode current=root;
long lastTreeNode=long.MinValue;
while(current!=null ||stack.Count>0)
{
//将所有左子节点存入这个栈中,而且最低下是根节点
while(current!=null)
{
stack.Push(current);
current=current.left;
}
//弹出栈的一个节点
current=stack.Pop();
//判断当前节点是否小于上一个节点,第一次进入的时候是跟最小值比,第一个节点值随便多大
if(current.val<=lastTreeNode)
{
return false;
}
//记下当前节点的值
lastTreeNode=current.val;
//将当前节点转为右子树届节点
current=current.right;
}
return true;
}
}
