【语义分割专栏】先导篇：评价指标(PA,CPA,IoU,mIoU,FWIoU,F1)

前言

本篇向大家介绍下语义分割任务中的常用的评价指标。该怎么评价语义分割模型的优劣以及好坏呢？以下就是些常用的评价指标。本篇文章收录于语义分割专栏，如果对语义分割领域感兴趣的，可以去看看专栏，会对经典的模型以及代码进行详细的讲解哦！其中会包含可复现的代码！

混淆矩阵

相信大家对这张图都不会陌生，这就是混淆矩阵。以上展示的是二分类的情况，后面给大家扩展到多分类的情况

那么到底啥是混淆矩阵呢？可能很多人都说不太出来。要知道混淆矩阵是一种用于评估分类模型性能的表格，它展示了模型预测结果与真实标签之间的对应关系。在多分类问题中，混淆矩阵可以帮助我们了解模型在各个类别上的表现，特别是哪些类别容易被混淆。这也是为什么叫混淆矩阵的原因。

混淆矩阵的行列分别代表以下内容：

• 行（垂直方向）：代表真实类别（True Class）。每一行对应一个真实类别，表示实际属于该类别的样本。
• 列（水平方向）：代表预测类别（Predicted Class）。每一列对应一个预测类别，表示模型预测为该类别的样本。

混淆矩阵中的元素表示相应真实类别和预测类别的样本数量。

如上图所示的，对于二分类问题，将类别1称为正例（Positive），类别2称为反例（Negative），分类器预测正确记作真（True），预测错误记作（False），由这4个基本术语相互组合，构成混淆矩阵的4个基础元素，为：

• TP（True Positive）：真正例，模型预测为正例，实际是正例（模型预测为类别1，实际是类别1）

• FP（False Positive）：假正例，模型预测为正例，实际是反例 （模型预测为类别1，实际是类别2）

• FN（False Negative）：假反例，模型预测为反例，实际是正例 （模型预测为类别2，实际是类别1）

• TN（True Negative）：真反例，模型预测为反例，实际是反例 （模型预测为类别2，实际是类别2）

所以到这，我们可以很明确从混淆矩阵中获取一些信息，其中对角线的为预测正确的类别数量，横着的为真实的，竖着的为预测的。

所以我们就可以计算一些指标：

准确率(Accuracy)：准确率是所有正确预测的样本数占总样本数的比例

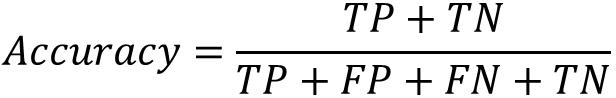
精确率(Precision)：精确率是所有正确预测的正例占预测为正例的样本数的比例。

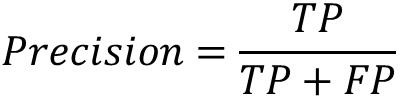
召回率(Recall)：召回率是所有正确预测的正例占实际正例的样本数的比例。

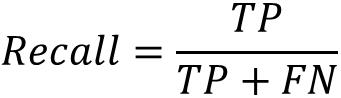
我们再来看多分类的情况，假设我们有一个3类分类问题，混淆矩阵如下所示：

|        | Predicted Class 0 | Predicted Class 1 | Predicted Class 2 |
|--------|--------------------|--------------------|--------------------|
| True 0 |        50          |        2           |        3           |
| Class  |                    |                    |                    |
| True 1 |        5           |        60          |        10          |
| Class  |                    |                    |                    |
| True 2 |        4           |        8           |        48          |
| Class  |                    |                    |                    |

那么我们的**准确率的计算就是对角线的值的和除以全部的值的和****。

即 acc = （50+60+48）/（50+2+3+5+60+10+4+8+48）

精确率就是对角线的值除以该列的值的和，例如类1：

即 Precision = 60 /（2+60+8）

召回率就是对角线的值除以该行的值的和，例如类1：

即 Recall = 60 /（5+60+10）

计算混淆矩阵

说了这么多，我们具体该如何去计算混淆矩阵呢？这里以语义分割任务为例。

def genConfusionMatrix(numClass,imgPredict, imgLabel):mask = (imgLabel >= 0) & (imgLabel < numClass)label = numClass * imgLabel[mask] + imgPredict[mask]count = np.bincount(label, minlength=numClass ** 2)confusionMatrix = count.reshape(numClass, numClass)return confusionMatrix

• 获得mask掩码

首先我们通过imgLabel图像标签获得mask掩码，通过这一步我们可以获得我们任务所需的符合要求的类别。其返回值是一个Bool矩阵，具体什么意思，看图。通过这样的方式，获得我们需要去计算的类别矩阵。

• 获得一维的label数组

然后看label的计算，非常重要，我们选择mask中True的来计算，计算过程就是$numClass\ast imgLabel[mask]+imgPredict[mask]$ ，并且我们得到的最终是一个一维的数组。

我们去理解混淆矩阵哈，我们对于该像素的预测，无论预测正确还是错误，是不是应该在其类别对应的那行，就是比如说其真实值是类5（从0开始哈），而我们预测成了类3，那么他肯定是第6行的某个预测的位置，而现在我们得到的label是一位数组，那我们乘以其类别数在加上预测的3，是不是就是这个像素应该在的混淆矩阵中的位置，只不过现在是一维的。

举个例子就是下图，我们一共有3个类，对于第一个像素的位置，真实值为类2，我们预测成了类1，在混淆矩阵中是不是应该是第三行的第二列，那么7是不是在一维数组中就是位于第三行的第二列的呢(从0开始的哈)。

• 计数并reshape

怎么计数我们用到$np.bincount(label,minlength=numClass\ast \ast 2)$这个函数。

# 我们可以看到x中最大的数为7，因此bin的数量为8，那么它的索引值为0->7
x = np.array([0, 1, 1, 3, 2, 1, 7])
# 索引0出现了1次，索引1出现了3次......索引5出现了0次......
np.bincount(x)
#因此，输出结果为：array([1, 3, 1, 1, 0, 0, 0, 1])# 我们可以看到x中最大的数为7，因此bin的数量为8，那么它的索引值为0->7
x = np.array([7, 6, 2, 1, 4])
# 索引0出现了0次，索引1出现了1次......索引5出现了0次......
np.bincount(x)
#输出结果为：array([0, 1, 1, 0, 1, 0, 1, 1])# 我们可以看到x中最大的数为3，因此bin的数量为4，那么它的索引值为0->3
x = np.array([3, 2, 1, 3, 1])
# 本来bin的数量为4，现在我们指定了参数为7，因此现在bin的数量为7，所以现在它的索引值为0->6
np.bincount(x, minlength=7)
# 因此，输出结果为：array([0, 2, 1, 2, 0, 0, 0])

然后我在将其转换shape就可以得到我们的混淆矩阵了。

评价指标

像素准确率(Pixel Accuracy,PA)

PA是最直观、最简单的指标，它计算预测正确的像素数占总像素数的比例，直接显示了模型对每个像素分类的准确度。在需要快速了解整体分类精度的场景中，这个指标非常有用。PA值越高，说明模型的预测越准确。如果PA等于1，意味着所有像素都被正确分类；而PA等于0，则表示所有像素都被错误分类。不过，这两种情况都相当极端，基本上不会出现。

得到我们的混淆矩阵后，PA指标就非常容易计算了。对角线的和除以总和即可。

def pixelAccuracy():acc = np.diag(confusionMatrix).sum() / confusionMatrix.sum()return acc

类别像素准确率(Class Pixel Accuracy,CPA)

CPA就是给每个类别单独算一下分类准不准，这样就能知道模型在处理不同类别的时候表现咋样。毕竟在语义分割里，不同的类别重要性和难易程度都不一样，通过CPA就能看出模型对哪些类别更擅长，哪些类别还不足。对某个类别来说，这个值越高，就说明这个类别的像素被分对的越多。

其实就是每个类别对应的召回率，注意这里是召回率哈，有些博客写错了都说是精确率，应该是召回率才对的。对角线的值除以该行的总和。

def classPixelAccuracy():denominator = confusionMatrix.sum(axis=1)denominator = np.where(denominator == 0, 1e-12, denominator)classAcc = np.diag(confusionMatrix) / denominatorreturn classAcc

类别平均像素准确率(Mean Pixel Accuracy,MPA)

MPA就是把每个类别的分类准确率加起来求平均，这样就能把所有类别的分类情况都考虑进去，不会只看总体情况而忽略了不同类别之间的差别。这个指标能让我们更全面地了解模型在处理不同类别时的平均表现。跟PA一样，MPA的值越高，说明模型在各个类别上的平均分类准确率也越高，它的取值范围在0到1之间。

就是CPA的和除以类别数

def meanPixelAccuracy():classAcc = classPixelAccuracy()meanAcc = np.nanmean(classAcc)return meanAcc

交并比(Intersection over Union,IoU)

IoU这个指标是通过计算预测结果和真实标签的交集和并集的比例来得出的，它能更好地反映预测区域和真实区域的重叠程度。相比单纯的像素准确率，IoU更关注物体的边界和形状是不是匹配，所以它能更准确地衡量模型的性能。IoU的值越高，说明预测结果和真实标签的重叠度越高，分割效果也越好。如果IoU等于1，那就表示预测区域和真实区域完全重合；如果IoU等于0，那就说明两者完全没有重叠。一般来说，IoU能达到0.5以上，就被认为是比较好的分割结果了。

这个怎么计算，同样的也是通过混淆矩阵，交集就是对角线的值，其实也就是预测正确的，并集就是在该对角线的值所在的行和列相加在减去该对角线的值即可，因为对角线的值加了两次。

def IntersectionOverUnion():intersection = np.diag(confusionMatrix)union = np.sum(confusionMatrix, axis=1) + np.sum(confusionMatrix, axis=0) - np.diag(confusionMatrix)union = np.where(union == 0, 1e-12, union)IoU = intersection / unionreturn IoU

平均交并比(Mean Intersection over Union,mIoU)

mIoU就是计算所有类别IoU的平均值，这个指标能综合评估模型在各个类别上的分割精度，可以说是语义分割任务中最重要的指标了。它能平衡不同类别之间的差异，更全面地反映模型的性能，所以在比较不同模型的时候，mIoU是一个比较可靠的指标。mIoU的取值范围在0到1之间，值越高代表模型在各个类别上的平均分割效果越好。一般来说，mIoU越高的模型，它的分割性能也越好。

def meanIntersectionOverUnion():mIoU = np.nanmean(IntersectionOverUnion())return mIoU

频率加权交并比(Frequency Weighted Intersection over Union,FWIoU)

FWIoU这个指标会考虑每个类别在数据里出现的次数，给交并比加权计算。这么一来，就不会只关注那些经常出现的类别，而忽略了那些不常出现的类别，评估结果更能反映模型在实际应用中的表现。FWIoU的值也在0到1之间，越高说明模型在考虑了类别出现频率后，分割效果越好。如果FWIoU接近1，那就说明模型对各种类别的分割都能很好地适应数据里的类别分布；如果FWIoU比较低，那就说明模型可能在某些经常出现或者很少出现的类别上分割得不太好。

def Frequency_Weighted_Intersection_over_Union():denominator1 = np.sum(confusionMatrix)denominator1 = np.where(denominator1 == 0, 1e-12, denominator1)freq = np.sum(confusionMatrix, axis=1) / denominator1denominator2 = np.sum(confusionMatrix, axis=1) + np.sum(confusionMatrix, axis=0) - np.diag(confusionMatrix)denominator2 = np.where(denominator2 == 0, 1e-12, denominator2)iu = np.diag(confusionMatrix) / denominator2FWIoU = (freq[freq > 0] * iu[freq > 0]).sum()return FWIoU

类别F1分数(Class F1 Score)

F1 分数结合了类别预测的精确率和召回率，对每个类别单独计算，能更细致地反映模型在不同类别上的分类性能。在一些既要求分类准确又要求不遗漏任何信息的场景中，F1 分数能提供更全面的评估信息。F1 分数的取值在 0 到 1 之间，值越高表示该类别上模型的分类性能越好。

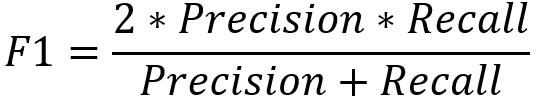
def classF1Score():tp = np.diag(confusionMatrix)fp = confusionMatrix.sum(axis=0) - tpfn = confusionMatrix.sum(axis=1) - tpprecision = tp / (tp + fp + 1e-12)recall = tp / (tp + fn + 1e-12)f1 = 2 * precision * recall / (precision + recall + 1e-12)return f1

平均F1分数(Mean F1 Score,mF1)

mF1就是把所有类别的F1分数加起来求平均，就能综合评估模型在各个类别上的整体表现，平衡了不同类别之间的差异，不会只盯着那些主要的类别而忽略了其他的类别，这样能更全面地反映模型的分类能力。mF1的取值范围在0到1之间，值越高代表模型在各个类别上的平均分类性能越好。

def meanF1Score():f1 = classF1Score()mean_f1 = np.nanmean(f1)return mean_f1

全部代码

import numpy as npclass SegmentationMetric(object):def __init__(self, numClass):self.numClass = numClassself.confusionMatrix = np.zeros((self.numClass,) * 2)def pixelAccuracy(self):acc = np.diag(self.confusionMatrix).sum() / self.confusionMatrix.sum()return accdef classPixelAccuracy(self):denominator = self.confusionMatrix.sum(axis=1)denominator = np.where(denominator == 0, 1e-12, denominator)classAcc = np.diag(self.confusionMatrix) / denominatorreturn classAccdef meanPixelAccuracy(self):classAcc = self.classPixelAccuracy()meanAcc = np.nanmean(classAcc)return meanAccdef IntersectionOverUnion(self):intersection = np.diag(self.confusionMatrix)union = np.sum(self.confusionMatrix, axis=1) + np.sum(self.confusionMatrix, axis=0) - np.diag(self.confusionMatrix)union = np.where(union == 0, 1e-12, union)IoU = intersection / unionreturn IoUdef meanIntersectionOverUnion(self):mIoU = np.nanmean(self.IntersectionOverUnion())return mIoUdef genConfusionMatrix(self, imgPredict, imgLabel):mask = (imgLabel >= 0) & (imgLabel < self.numClass)label = self.numClass * imgLabel[mask] + imgPredict[mask]count = np.bincount(label, minlength=self.numClass ** 2)confusionMatrix = count.reshape(self.numClass, self.numClass)return confusionMatrixdef Frequency_Weighted_Intersection_over_Union(self):denominator1 = np.sum(self.confusionMatrix)denominator1 = np.where(denominator1 == 0, 1e-12, denominator1)freq = np.sum(self.confusionMatrix, axis=1) / denominator1denominator2 = np.sum(self.confusionMatrix, axis=1) + np.sum(self.confusionMatrix, axis=0) - np.diag(self.confusionMatrix)denominator2 = np.where(denominator2 == 0, 1e-12, denominator2)iu = np.diag(self.confusionMatrix) / denominator2FWIoU = (freq[freq > 0] * iu[freq > 0]).sum()return FWIoUdef classF1Score(self):tp = np.diag(self.confusionMatrix)fp = self.confusionMatrix.sum(axis=0) - tpfn = self.confusionMatrix.sum(axis=1) - tpprecision = tp / (tp + fp + 1e-12)recall = tp / (tp + fn + 1e-12)f1 = 2 * precision * recall / (precision + recall + 1e-12)return f1def meanF1Score(self):f1 = self.classF1Score()mean_f1 = np.nanmean(f1)return mean_f1def addBatch(self, imgPredict, imgLabel):assert imgPredict.shape == imgLabel.shapeself.confusionMatrix += self.genConfusionMatrix(imgPredict, imgLabel)return self.confusionMatrixdef reset(self):self.confusionMatrix = np.zeros((self.numClass, self.numClass))def get_scores(self):scores = {'Pixel Accuracy': self.pixelAccuracy(),'Class Pixel Accuracy': self.classPixelAccuracy(),'Intersection over Union': self.IntersectionOverUnion(),'Class F1 Score': self.classF1Score(),'Frequency Weighted Intersection over Union': self.Frequency_Weighted_Intersection_over_Union(),'Mean Pixel Accuracy': self.meanPixelAccuracy(),'Mean Intersection over Union(mIoU)': self.meanIntersectionOverUnion(),'Mean F1 Score': self.meanF1Score()}return scoresif __name__ == "__main__":num_classes = 3generator = SegmentationMetric(num_classes)img_predict = np.random.randint(0, num_classes, size=(4, 4))img_label = np.random.randint(0, num_classes, size=(4, 4))matrix = generator.addBatch(img_predict, img_label)print("预测图像矩阵:")print(img_predict)print("标签图像矩阵:")print(img_label)print("混淆矩阵:")print(matrix)scores = generator.get_scores()for k, v in scores.items():if isinstance(v, np.ndarray):print(f"{k}: {np.round(v, 3)}")else:print(f"{k}: {v:.4f}")

结语

希望上列所述内容对你有所帮助，如果有错误的地方欢迎大家批评指正！

如果你觉得讲的还不错想转载，可以直接转载，不过麻烦指出本文来源出处即可，谢谢！

参考内容

本文参考了下列的文章内容，集百家之长汇聚于此，同时包含自己的思考想法

Python计算语义分割模型的评价指标_混淆矩阵算f1score-CSDN博客

语义分割的评价指标——PA(像素准确率)、CPA(类别像素准确率)、MPA(类别平均像素准确率)、IoU(交并比)、MIoU(平均交并比)详细总结_dice score-CSDN博客

【语义分割】评价指标代码函数：np.sum()、np.nansum()、np.nanmean()、np.diag()、np.bincount()_语义分割评价代码-CSDN博客

numpy.bincount详解_np.bincount-CSDN博客

【语义分割】评价指标：PA、CPA、MPA、IoU、MIoU详细总结和代码实现（零基础从入门到精通系列！）_语义分割指标-CSDN博客