当前位置： 首页 > news >正文

数据结构第七章（二）-树形查找：二叉排序树与平衡二叉树

news 来源：原创 2025/5/15 9:03:05

树形查找（一）

  • 二叉排序树与平衡二叉树
  • 一、二叉排序树
    • 1.查找
    • 2.插入
    • 3.删除
    • 4.查找效率分析
  • 二、平衡二叉树
    • 1.插入
      • 1.1 LL
      • 1.2 RR
      • 1.3 LR
      • 1.4 RL
    • 2.插入的查找效率分析
    • 3.删除
  • 总结

二叉排序树与平衡二叉树

一、二叉排序树

二叉排序树，又称二叉查找树（BST，Binary Search Tree）

一棵二叉树或者是空二叉树，或者是具有如下性质的二叉树：

  • 左子树上的所有结点的关键字均小于根结点的关键字；
  • 右子树上的所有结点的关键字均大于根结点的关键字；
  • 左子树和右子树又各是一棵二叉排序树。

比如下面这个水灵灵的二叉排序树：

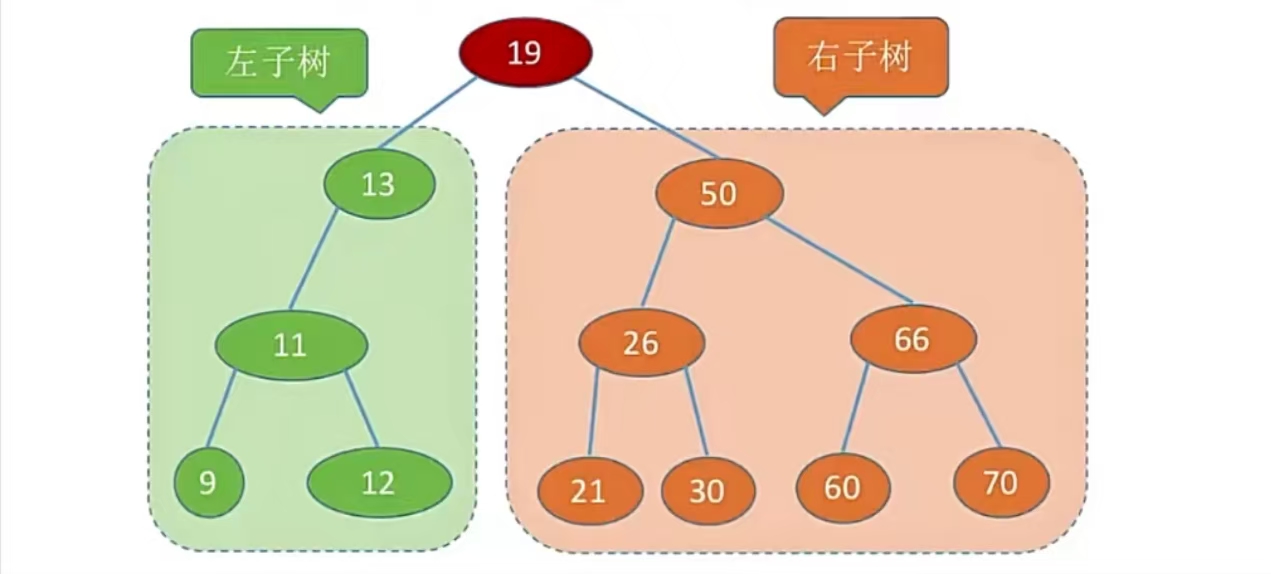
在这里插入图片描述

所以二叉排序树一定是左<根<右的，即：

左子树结点值<根结点值<右子树结点值

进行中序遍历，可以得到一个递增的有序序列

所以根据这个性质，二叉排序树可用于元素的有序组织、搜索

1.查找

我们知道，二叉排序树的左子树结点值<根结点值<右子树结点值，所以在这里查找的话，就看关键字是大了还是小了，大了的话就往右走，小了的话就往左走，直到找到或者找不到为止就可以了。

  • 若树非空，目标值与根结点的值比较；
  • 若相等，则查找成功；
  • 若小于根节点，则在左子树上查找，否则在右子树上查找。

查找成功，返回结点指针；查找失败则返回NULL

代码比较清晰：


//二叉排序树的结点
typedef struct BSTNode{int key;struct BSTNode *lchild,*rchild;
}BSTNode, *BSTree;//在二叉排序树中查找值为 key的结点
BSTNode *BST_Search(BSTree T, int key){while(T != NULL && key != T->key){ //若树空或等于根节点值，则结束循环if(key < T->key){       //小于，则在左子树上查找T = T->lchild;      //大于，则在右子树上查找}else{T = T->rchild;}}return T;
}

比如下面这张图:

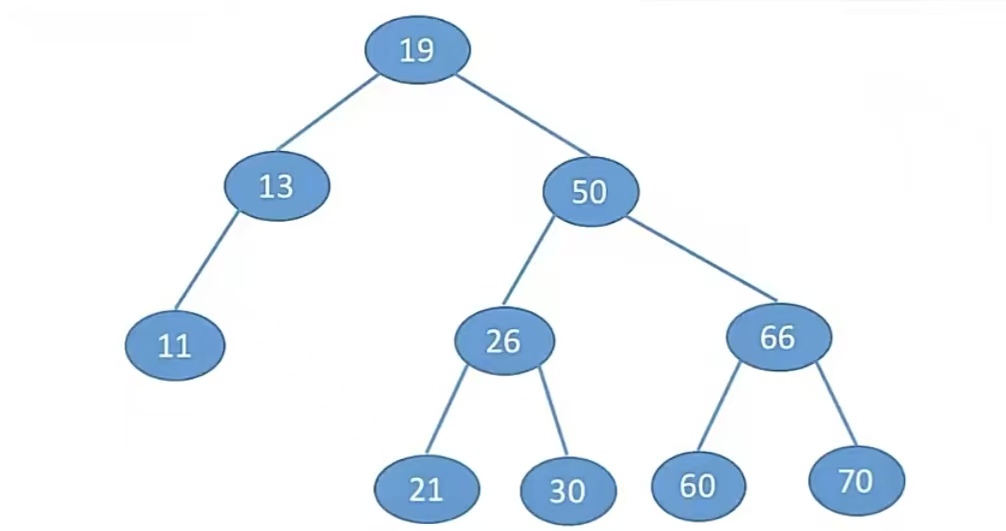
在这里插入图片描述
举个栗子，如果我们想要查找关键字为30的结点，先和根节点对比，发现19<30，找它的右孩子比；发现50>30，再找它的左孩子比；发现26<30，再找它的右孩子比；发现30=30，查找成功；

如果我们想要查找关键字为12的结点，也是重复这个流程；直到和11比，发现30>11，但是右孩子为NULL，所以T就变成了NULL，返回NULL查找失败。

上述算法过程也可以用递归来实现：


//二叉排序树的结点
typedef struct BSTNode{int key;struct BSTNode *lchild,*rchild;
}BSTNode, *BSTree;//在二叉排序树中查找值为key的结点（递归实现）
BSTNode *BST_Search_Recursion(BSTree T, int key){if(T == NULL){return NULL;    //查找失败}if(key == T->key){return T;       //查找成功}else if(key < T->key){return BST_Search_Recursion(T->lchild, key);//在左子树中找}else{return BST_Search_Recursion(T->rchild, key);//在右子树中找}}

一样的其实。

但是显然空间复杂度不一样，因为我们递归有递归调用栈嘛，所以普通二叉排序树查找的最坏空间复杂度是O(1)，但是递归查找的最坏时间复杂度是O(h)，所以需要看情况酌情使用。

2.插入

插入的话肯定是要先知道插到哪里，和上述的查找一样的；还有就要注意下我们的插入是如果在BST中找到了这个关键字就不插入了。

若原二叉排序树为空，则直接插入结点；否则，若关键字key小于根节点值，则插入到左子树，若关键字key大于根结点值，则插入到右子树。


//二叉排序树的结点
typedef struct BSTNode{int key;struct BSTNode *lchild,*rchild;
}BSTNode, *BSTree;//在二叉排序树中插入关键值为key的新结点（递归实现）
int BST_Insert(BSTree &T, int key){if(T == NULL){      //原树为空，新插入的结点为根节点T = (BSTree)malloc(sizeof(BSTNode))；T->key = k;T->lchild = T->rchild = NULL;return 1;       //返回1，插入成功}else if(k == T->key){ //树中存在相同关键字的结点，插入失败return 0;}else if(k < T->key){   //插入到T的左子树return BST_Insert(T->lchild, key);}else{                  //插入到T的右子树return BST_Insert(T->rchild, key);}
}

举个栗子，还是上面那张图，如果插入关键字为12的结点，首先递归找到要插入的位置，发现找到了结点11时，应该插入的11的右结点为空，我们到了递归出口，然后开始执行插入操作并返回成功即可。

由于是递归实现，所以我们二叉排序树插入的最坏空间复杂度也是O(h)，最新插入的结点一定是叶子结点。

那我们既然会插入了，其实也就会构造一棵二叉树了，因为你创建一棵二叉树的本质不就是把飘着的结点一个一个插进去吗，所以我们也就会构造一棵二叉树了，代码也是直接调用就可以了：

//按照str[]中的关键字序列建立二叉排序树
void create_BST(BSTree &T, int str[], int n){T = NULL;       //初始时T为空树int i = 0;while(i < n){   //依次将每个关键字插入到二叉排序树中BST_Insert(T, str[i]);i++;}
}

不过我们在构造二叉树的时候，不同的关键字序列得到的二叉树可能不同也可能相同，比如{2，1，3}和{2，1，3}，得到的就是同款二叉排序树。

3.删除

删除的话会有点麻烦，因为它是要分情况的。比如你要删除一个结点，那肯定不能哐哐删除就啥也不管了（当然删叶子结点是这样的），但是如果它还有左右孩子啥的，那你就得考虑用什么来占上它的位置，才能保证我们的树仍然满足二叉排序树的性质（左子树结点值<根结点值<右子树结点值），让它仍然是一棵水灵灵的二叉排序树。

当然我们要想删，那还是要先进行查找操作的，总要先找到它在哪才可以删了。

先搜索找到目标结点：

  • 若被删除结点z是叶结点，则直接删除，不会破坏二叉排序树的性质;
  • 若结点z只有一棵左子树或右子树，则让z的子树称为z双亲结点的子树，替代z的位置；
  • 若结点z有左、右两棵子树，则令z的直接后继（或直接前驱）替代z，然后从二叉排序树中删去这个直接后继（直接前驱），这样就转换成了第一或第二种的情况。

第一、第二种情况都比较好理解，主要是第三种左右孩子都有的情况，我们为什么要用中序遍历的后继/前驱来替代它呢？因为进行中序遍历，可以得到一个递增的有序序列，所以为了保持我们BST的特性，这样是最方便快捷的办法。

举个栗子，比如下面这张图：

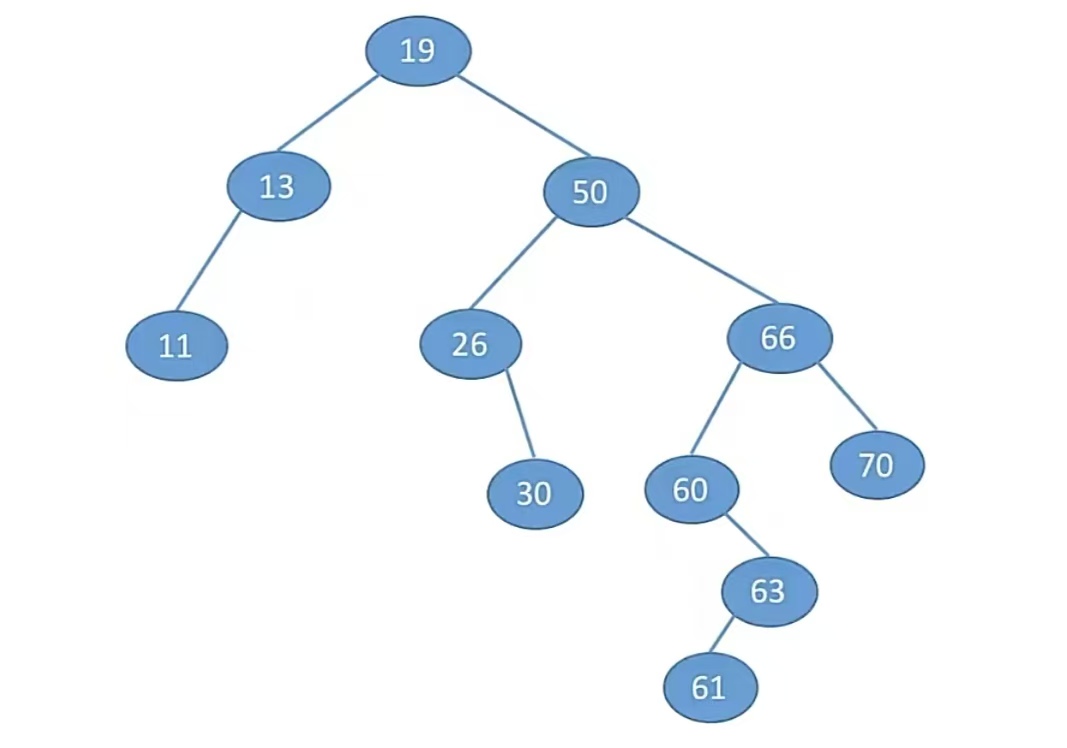
在这里插入图片描述

我们要删掉“50”这个结点，它既有左孩子，也要右孩子。如果我们要想用它的直接后继来代替它，那就只要找它的中序后继就可以了。也就是右子树中最先中序遍历的那个，即“60”，当用“60”换到“50”的位置上的时候，现在的问题就转化为了“删除60”，再看“60”有没有左右孩子，发现是有个右孩子的，所以直接用右孩子代替“60”就行了；

如果我们想用它的直接前驱来代替它，那么我们需要找到它的中序前驱，也就是左子树中最后中序遍历的那个，即“30”，当用“30”换到“50”的位置上的时候，现在的问题就转化为了“删除30”，再看“30”有没有左右孩子，发现是没有的，所以我们直接删除叶子结点就可以了。

简单来说，找中序前驱就是找左子树中的最右下结点，找中序后继就是找右子树中的最左下结点，因为中序遍历“左根右”嘛。

弱弱说一句，为什么如果它有左右孩子，删除的时候找中序前驱/后继删除，就一定能变成前面的两种情况，而不是继续“左右孩子都有”的情况呢？这是因为如果我们要找它的中序前驱，那既然满足是中序前驱，肯定是左子树里面进行了“左根右”的那个最后遍历的，也就是“最右下”，它一定没有右子树（因为有的话就不是最后遍历的了），所以一定不会又变成第三种情况，中序后继同理。

4.查找效率分析

那当然还是看我们的查找长度了，还记得什么是查找长度吗？在上一篇了，重复一下：

查找长度——在查找运算中，需要对比关键字的次数称为查找长度，反映了查找操作时间复杂度。

我们看看二叉排序树的查找效率，下面给出两棵二叉排序树：

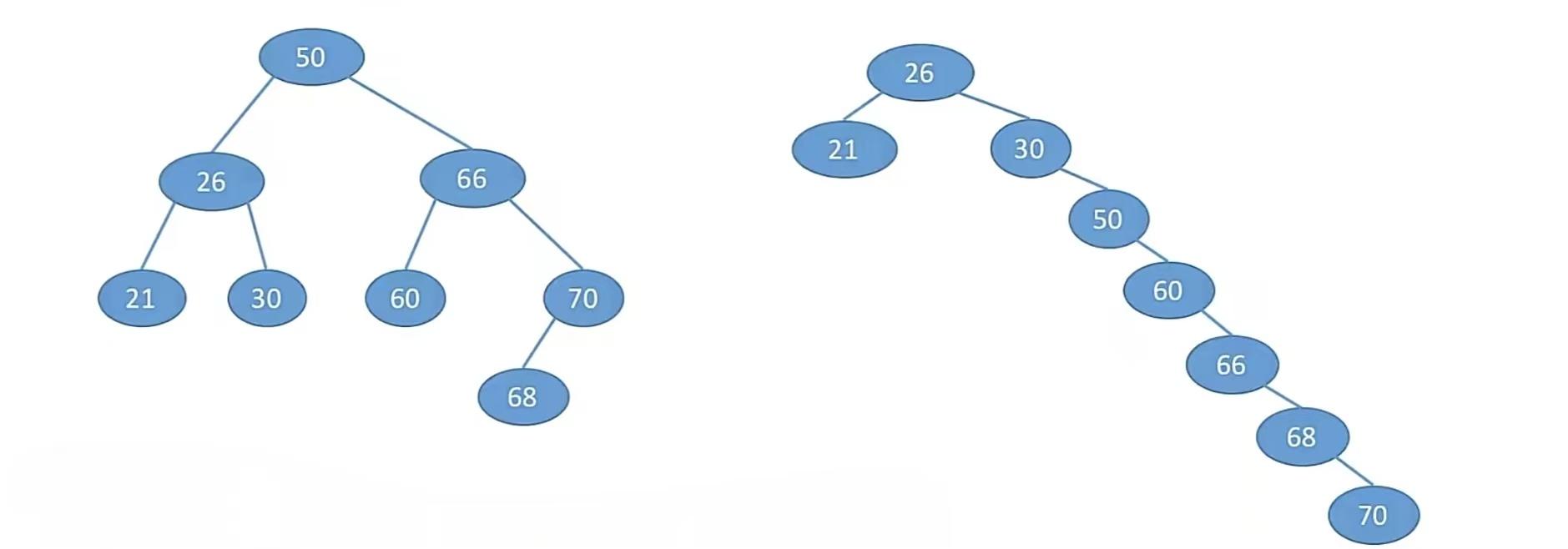
在这里插入图片描述

第一棵树：
查找成功的平均查找长度ASL = （1 * 1 + 2 * 2 + 3 * 4 + 4 * 1 ）/ 8 = 2.625

第二棵树：
查找成功的平均查找长度ASL = （1 * 1 + 2 * 2 + 3 * 1 + 4 * 1 + 5 * 1 + 6 * 1 + 7 * 1 ）/ 8 = 3.75

若树高h，找到最下层的一个结点要对比h次

最好情况：n各节点的二叉树的最小高度为⌊log2n⌋ + 1，平均查找长度=O(log2n)

最坏情况：每个结点只有一个分支，树高h=结点数n，平均查找长度=O(n)。

所以平衡二叉树最好了，平衡二叉树是树上任一结点的左子树和右子树的深度之差不超过1的树，它特别优秀，下面就讲了。

……我们刚刚其实只说了查找成功的情况，失败还没说呢，看下面的图，说完就开始说平衡二叉树：

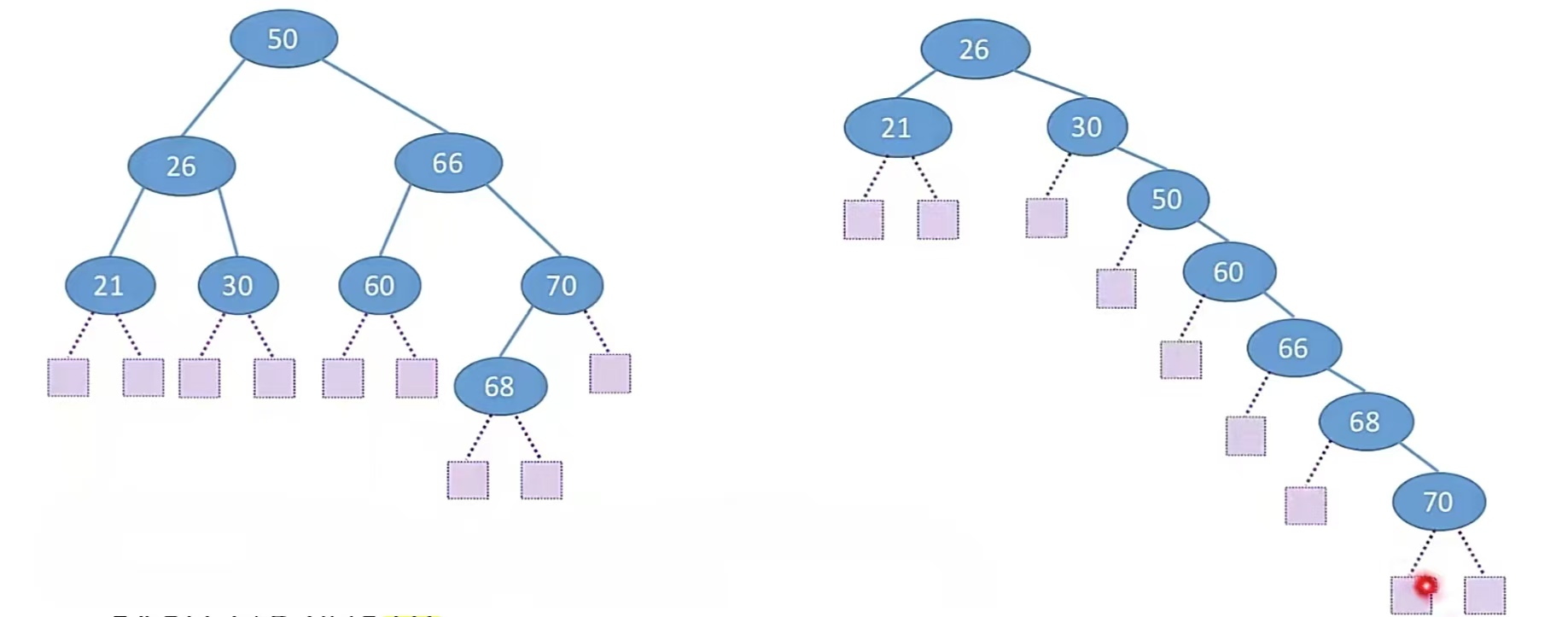
在这里插入图片描述

第一棵树：
查找失败的平均查找长度ASL = （3 * 7 + 4 * 2 ）/ 9 = 3.22

第二棵树：
查找失败的平均查找长度ASL = （ 2 * 3 + 3 * 1 + 4 * 1 + 5 * 1 + 6 * 1 + 7 * 2 ）/ 9 = 4.22

二、平衡二叉树

平衡二叉树是一种特殊的二叉排序树，人如其名，比较平衡，不会出现那种左子树长的不得了，右子树就一个啥的情况。左右子树差距最多就是1，又叫AVL树，因为这是两个人（G.M. Adelson-Velsky 和 E.M.Landis）搞出来的，所以就简称 AVL。

平衡二叉树（Balance Binary Tree），简称平衡树（AVL树）——树上任一结点的左子树和右子树的高度之差不超过1

结点的平衡因子 = 左子树高 - 右子树高

所以我们知道：

  • 平衡二叉树结点的平衡因子的值只可能是 -1、0 或者 1
  • 只要有任一节点的平衡因子绝对值大于1，就不是平衡二叉树

那么结点的定义就很明确了，只需要加上平衡因子就可以了，其他的和二叉树一样。

//平衡二叉树结点
typedef struct AVLNode{int key;        //数据域int balance;    //平衡因子struct AVLNode *lchild,*rchild;
}AVLNode,*AVLTree;

平衡二叉树的增删也是要注意的，要保证增删完它还是个平衡二叉树，尤其是插入，会比较麻烦。

1.插入

我们插入一个新结点后，查找路径上的所有结点都有可能受到影响。比如下面这张图，插入“67”后，就不再是一棵平衡二叉树了：

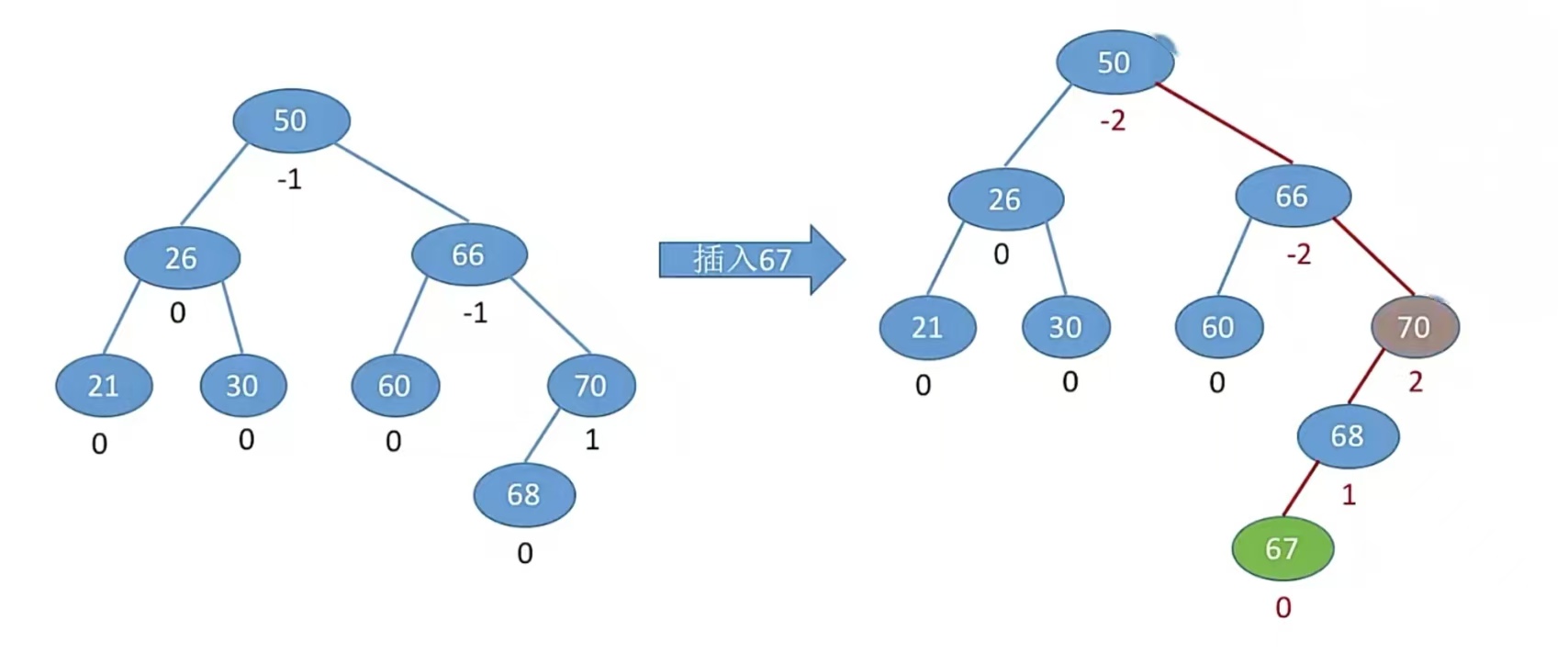
在这里插入图片描述

所以我们要做的就是，自己给它再调整成平衡二叉树。怎么调整呢？其实就是从插入点往回找到第一个不平衡结点，调整以该结点为根的子树，调整它就可以了。当然对于上面那个图而言，显然第一个不平衡结点是“70”；

所以我们每次调整的对象都是“最小不平衡子树”

在插入操作中，只要将最小不平衡子树调整平衡，则其他祖先结点都会恢复平衡。

我们根据插入的结点相对于第一个不平衡结点A的位置，把插入导致不平衡的情况分为四种：LL（在A的左孩子的左子树中插入导致不平衡），RR（在A的右孩子的右子树中插入导致不平衡），LR（在A的左孩子的右子树中插入导致不平衡），RL（在A的右孩子的左子树中插入导致不平衡），因人而异，针对不同情况给出不同的方案，这样方便我们归类汇总。

1.1 LL

我们先来讲讲这个是怎么回事，然后再拿刚刚那个图举例子（因为刚刚那个图插入其实也就是LL嘛）。首先我们知道LL是在A的左孩子的左子树中插入导致不平衡，原本是平衡的，那么就可以简化成这样：
//图1

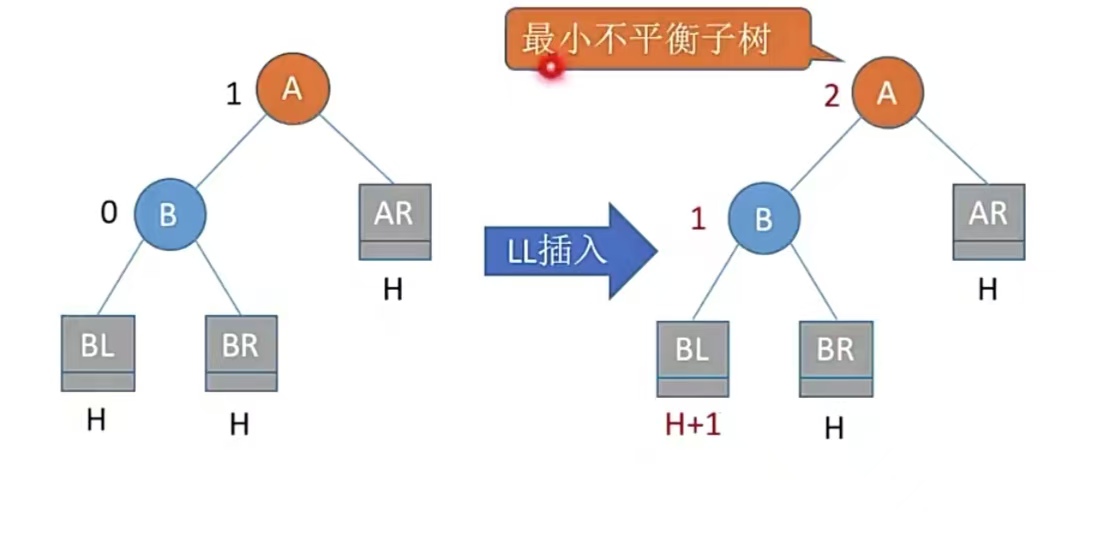
这样简化主要是为了表示出，左边这棵树还是平衡的（BL高度为H，BR高度为H，AR高度为H），但是在左子树中插入左孩子，就不平衡了（BL高度为H+1，BR高度为H，AR高度为H），A是不最小不平衡子树。（假定所有子树的高度为H，这样就能方便我们观察，插入直接导致A不平衡，该怎么办）。

此时我们就有两个目标：

1.恢复平衡；2.保持二叉排序树的特性

恢复平衡容易，但是要一遍恢复平衡，一边还保持二叉排序树的特性（左<根<右，BL＜B＜BR＜A＜AR）就不容易了，我们通过进行旋转来解决。

我们进行LL平衡旋转（右单旋转）。由于在结点A的左孩子（L）的左子树（L）上插入了新结点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根节点，将A结点向右下旋转成为B的右子树的根结点，而B的原右子树则作为A结点的左子树，如图：

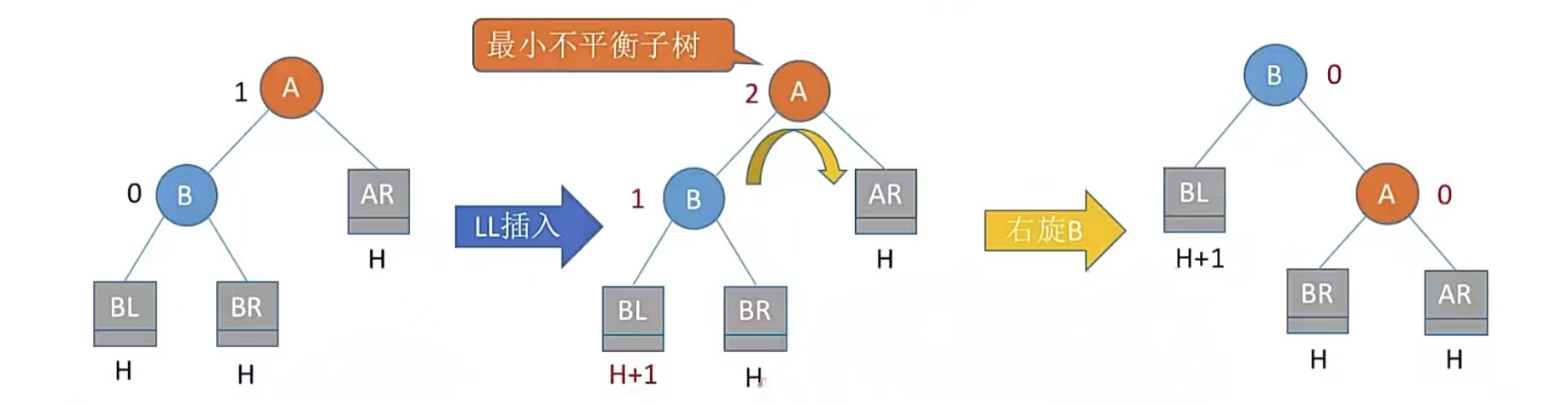
在这里插入图片描述

向右旋转了一下，B变成了根节点，B的右结点变成了A的左结点。这样的话我们既可以保证它由不平衡变成平衡，又可以保证这还是一棵二叉排序树，大同了。

所以刚刚那个栗子按照这个应该怎么办呢？就是调整以70为顶点的子树，对它进行“右旋”，即如图：

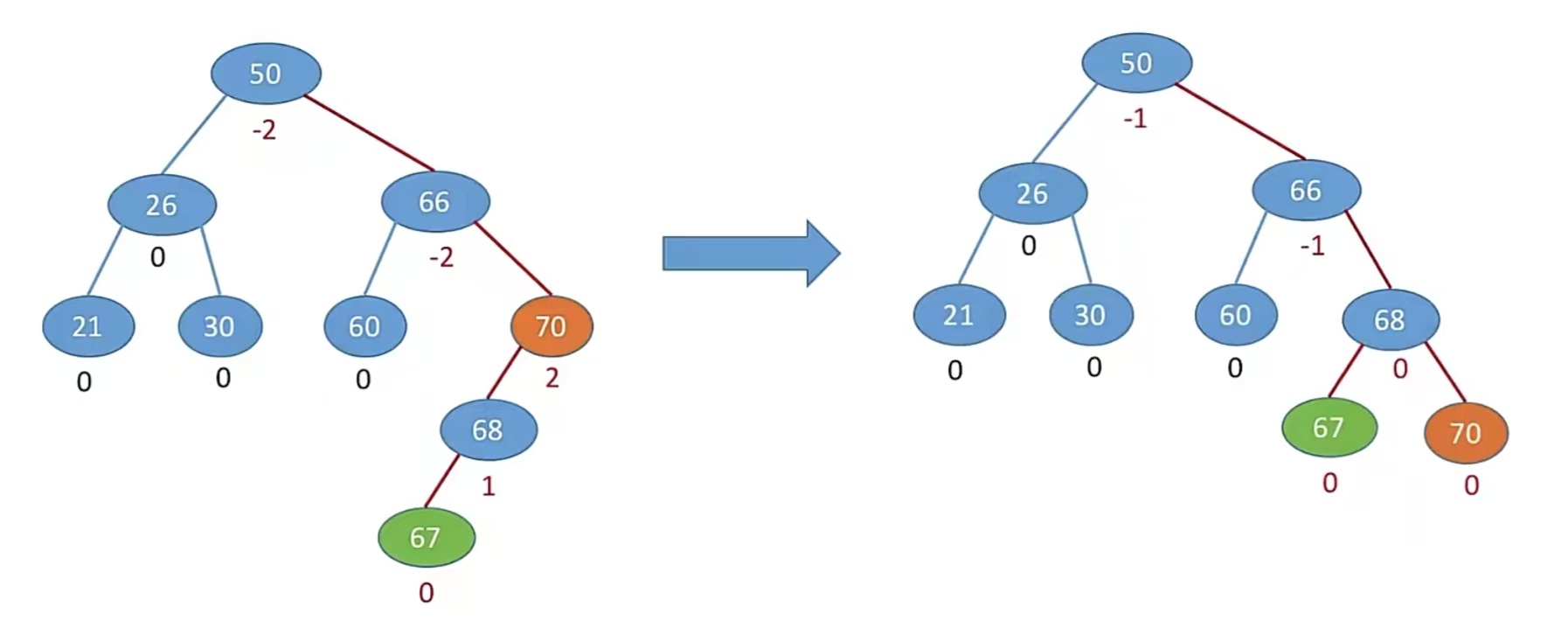
在这里插入图片描述
其实还是很简单的。

1.2 RR

刚刚说了LL，现在来看RR。RR就是在A的右孩子的右子树中插入导致不平衡，其实和LL很像，一个是左子树插入左孩子，一个是右子树插入右孩子，所以显而易见，LL应该“右旋”，那么RR就应该“左旋”。

我们先看RR怎么导致不平衡的：
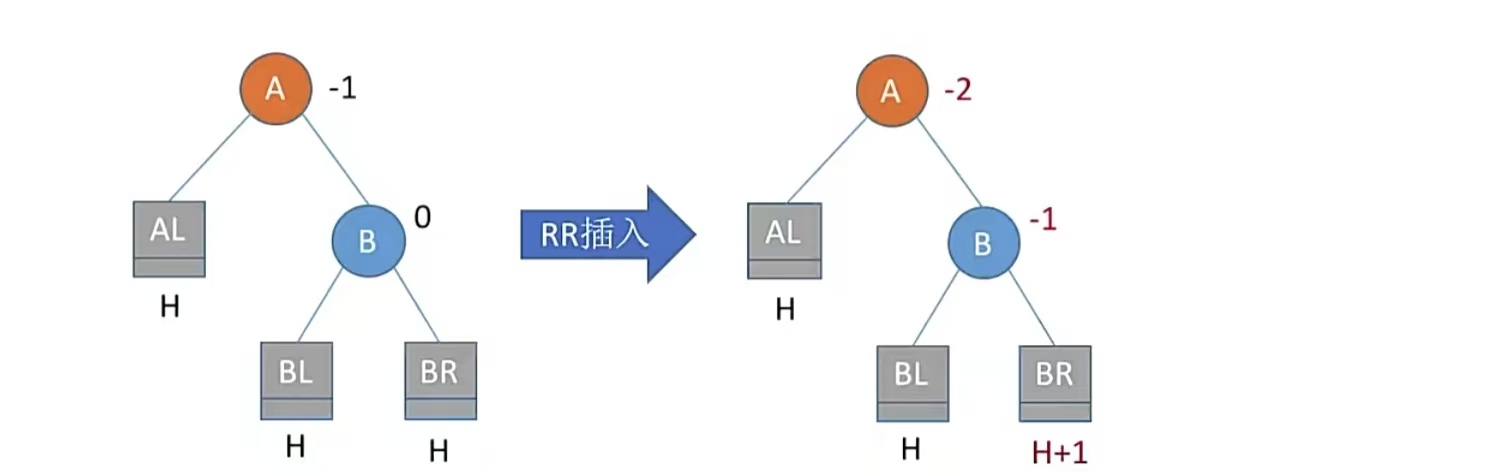
在这里插入图片描述

BR的高度由H变为H+1，导致结点A不平衡，结点A为根的子树是最小不平衡子树。所以我们应该进行“左旋”，即

我们进行RR平衡旋转（左单旋转）。由于在结点A的右孩子（R）的右子树（R）上插入了新结点，A的平衡因子由-1减至-2，导致以A为根的子树失去平衡，需要一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根节点，将A结点向左下旋转成为B的左子树的根节点，而B的原左子树则作为A结点的右子树。如图：

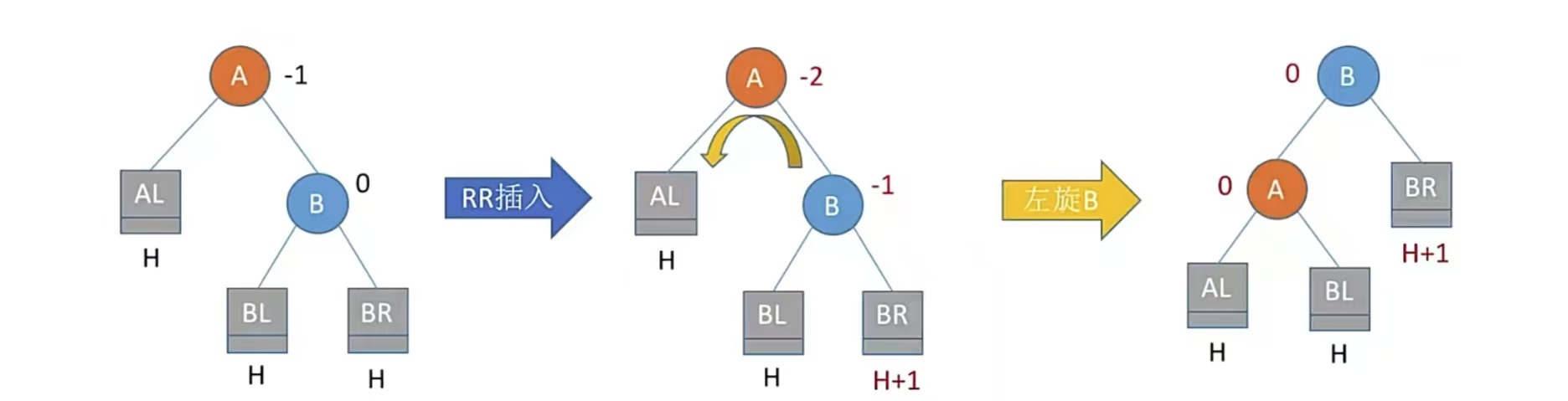
在这里插入图片描述
左旋后既能保证平衡又能保证二叉排序树的特性，即左旋后AL<A
<BL<B<BR也是满足的。

那么刚刚说了LL和RR，一个右旋一个左旋，所谓“旋转”代码思路是什么呢？其实就是一步一步来：
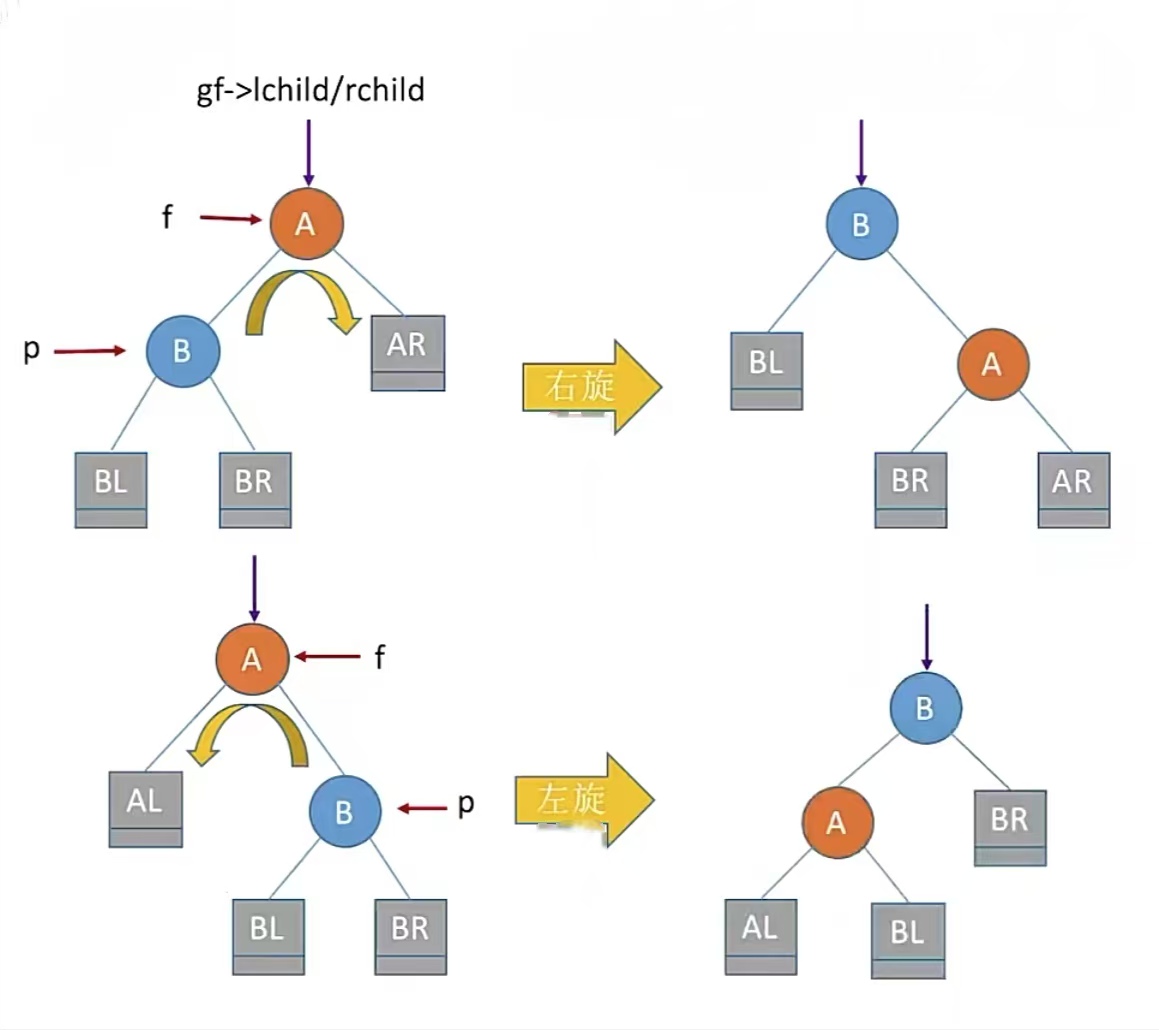
在这里插入图片描述

右旋：

实现f向右下旋转，p向由上旋转：
其中f是双亲结点，p为左孩子，gf为f的双亲结点

  • f->lchild = p->rchild;
  • p->rchild = f;
  • gf->lchild/rchild = p;

其实就是先让B的右孩子变成A的左孩子，然后再把A变成B的右孩子，最后再让A原来的双亲结点的孩子变成B（因为B代替了A的位置）。

左旋：

实现f向左下旋转，p向左上旋转：
其中f是双亲结点，p为右孩子，gf为f的双亲结点

  • f->rchild = p->lchild;
  • p->lchild = f;
  • gf->lchild/rchild = p;

这个也是一样的，其实就是先让B的左孩子变成A的右孩子，然后再把A变成B的左孩子，最后再让A原来的双亲结点的孩子变成B。

左旋、右旋操作后可以保持二叉排序树的特性哈

1.3 LR

LR，是在A的左孩子的右子树中插入导致不平衡，那么从现在开始就和上面不一样了，不是单纯的依次左旋/右旋就可以解决的了。先看看LR插入导致不平衡：
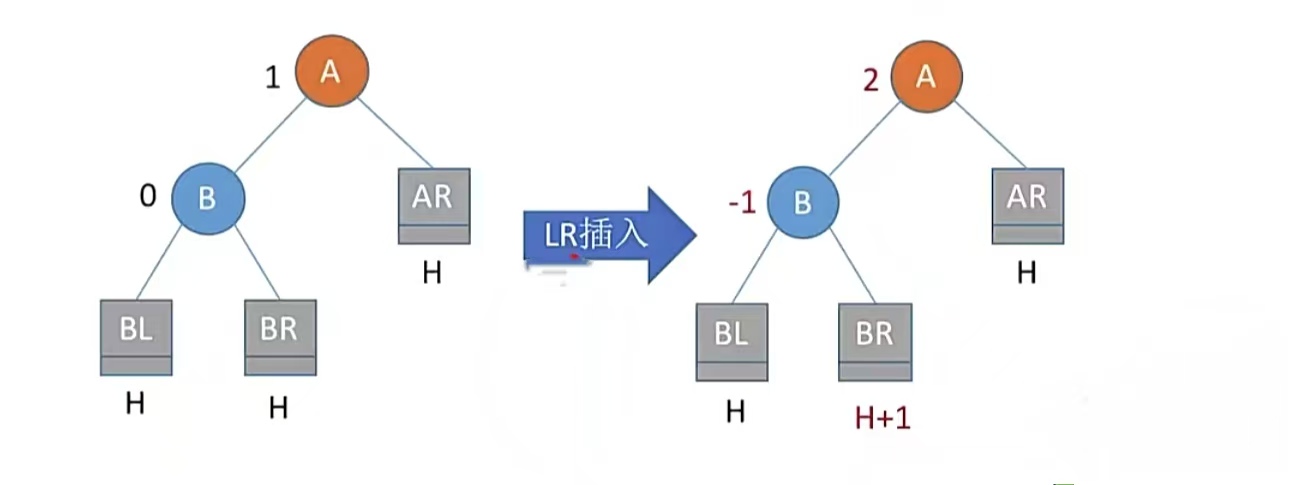
在这里插入图片描述

显然是在BR高度变为H+1后导致了A结点不平衡，那么往小了看也就是在B节点的右子树种插入了一个结点让以B结点为根的树高度增加导致的。我们假设B结点的右孩子为C结点，那么就是在C结点的左子树/右子树中插入了一个结点，如下所示：
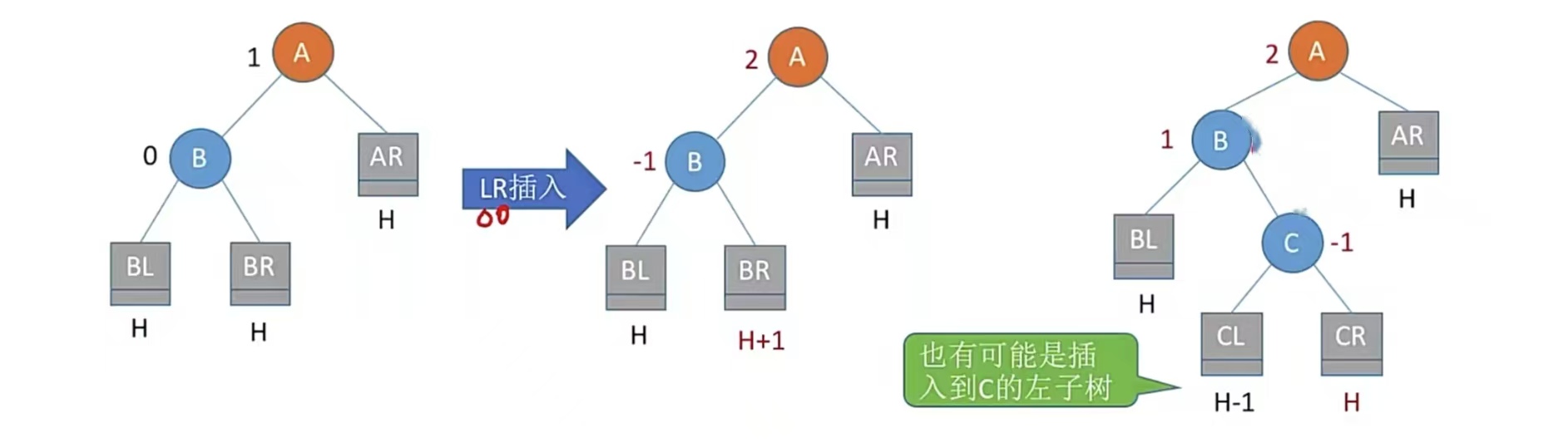
在这里插入图片描述

so 我们进行LR平衡旋转（先左后右双旋转）。由于在A的左孩子（L）的右子树（R）上插入新节点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先左旋转后右旋转。

先将A节点的左孩子B的右子树的根节点C向左上旋转提升到B结点的位置，然后再把该C结点向右上旋转提升到A结点的位置。

什么意思呢？看图：

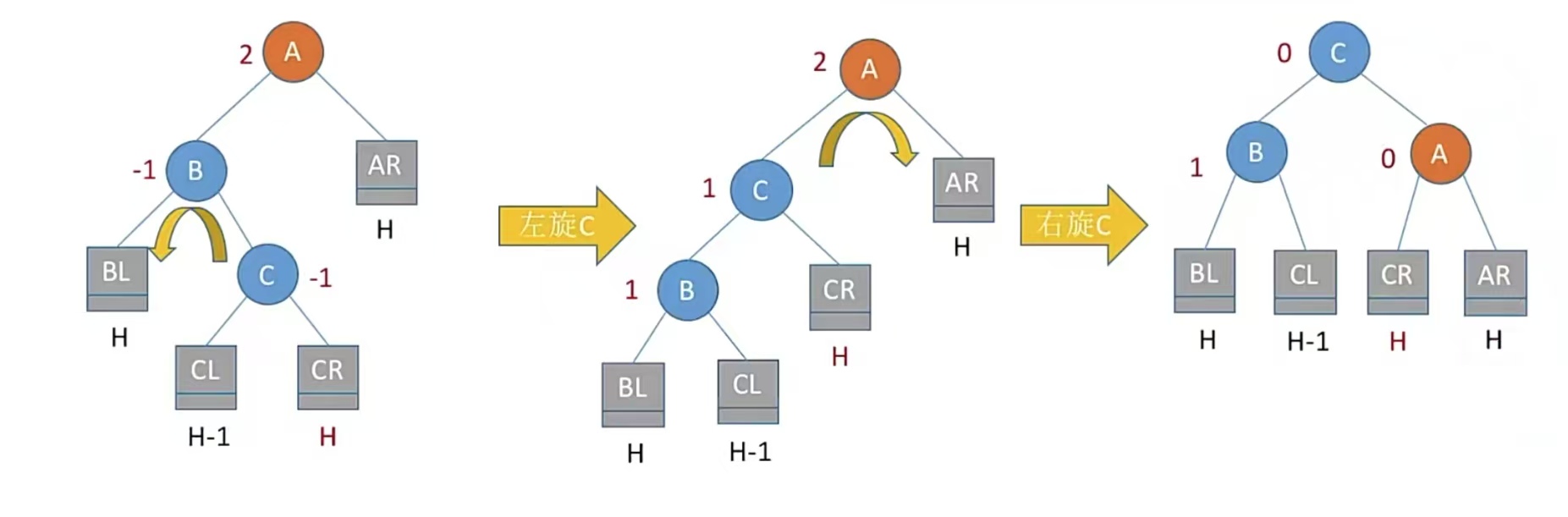
在这里插入图片描述

看着很麻烦，但其实就是转了两次。先把C的左孩子变成B的右孩子，再让B变成C的左孩子，然后再让C的右孩子变成A的左孩子，再让A变成C的右孩子。

简单来说就是先让C到B的位置，再让C到A的位置。因为C是A左孩子的右孩子，所以C到B要左旋，再到A要右旋，就是这样，没别的。这样旋转过后，还是满足BL<B<CL<C<CR<A<AR，符合二叉排序树且平衡。

我们假设的是C的左子树高度为H-1，右子树高度为H（新结点插到C的右子树上），其实C的左子树高度为H，右子树高度为H-1也是一样的转（新结点插到了左子树上），没什么区别。

我们还剩下最后一种情况，RL

1.4 RL

RL，在A的右孩子的左子树中插入导致不平衡，我们先看看怎么不平衡的（A结点的平衡因子变为-2）：

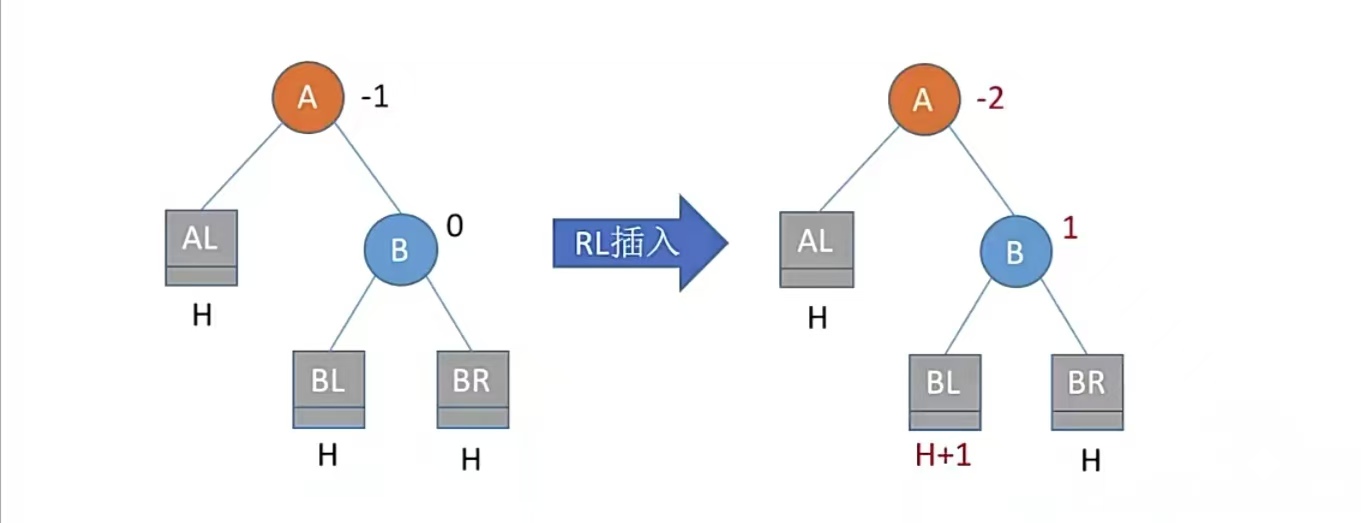
在这里插入图片描述

显然是在BL高度变为H+1后导致了A结点不平衡。我们假设B结点的左孩子为C结点，那么就是在C结点的左子树/右子树中插入了一个结点，如下所示：

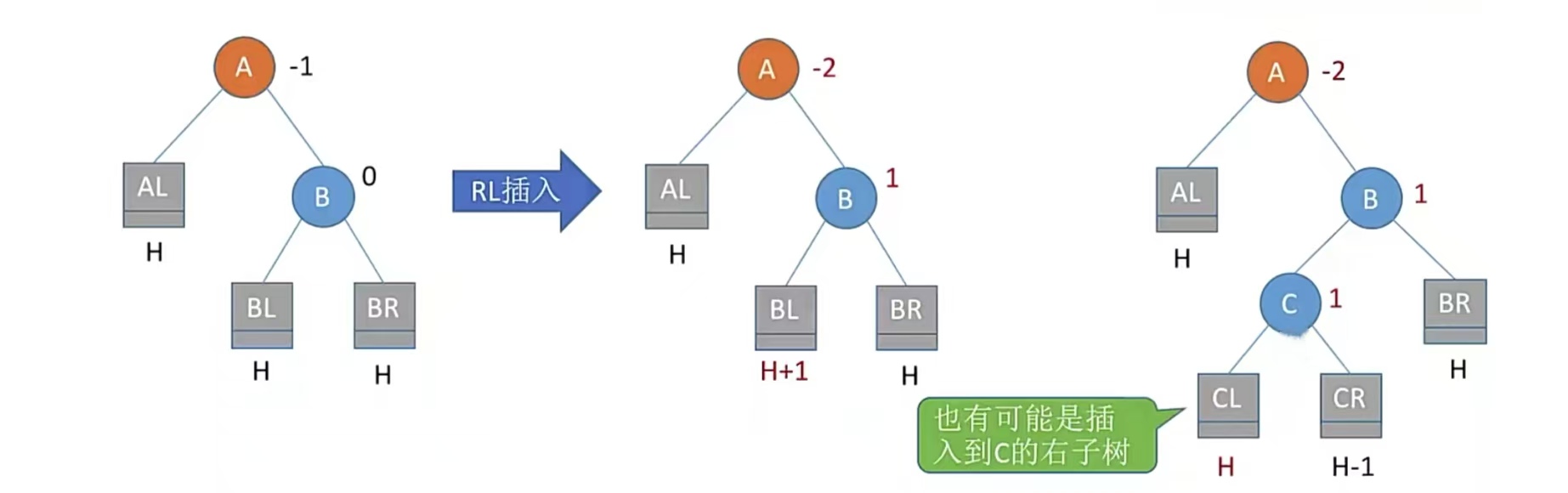
在这里插入图片描述

我们进行RL平衡旋转（先右后左双旋转）。由于在A的右孩子（R）的左子树（L）上插入新节点，A的平衡因子由-1减至-2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先右旋转后左旋转。

先将A节点的右孩子B的左子树的根节点C向右上旋转提升到B结点的位置，然后再把该C结点向左上旋转提升到A结点的位置。

也就是这样：

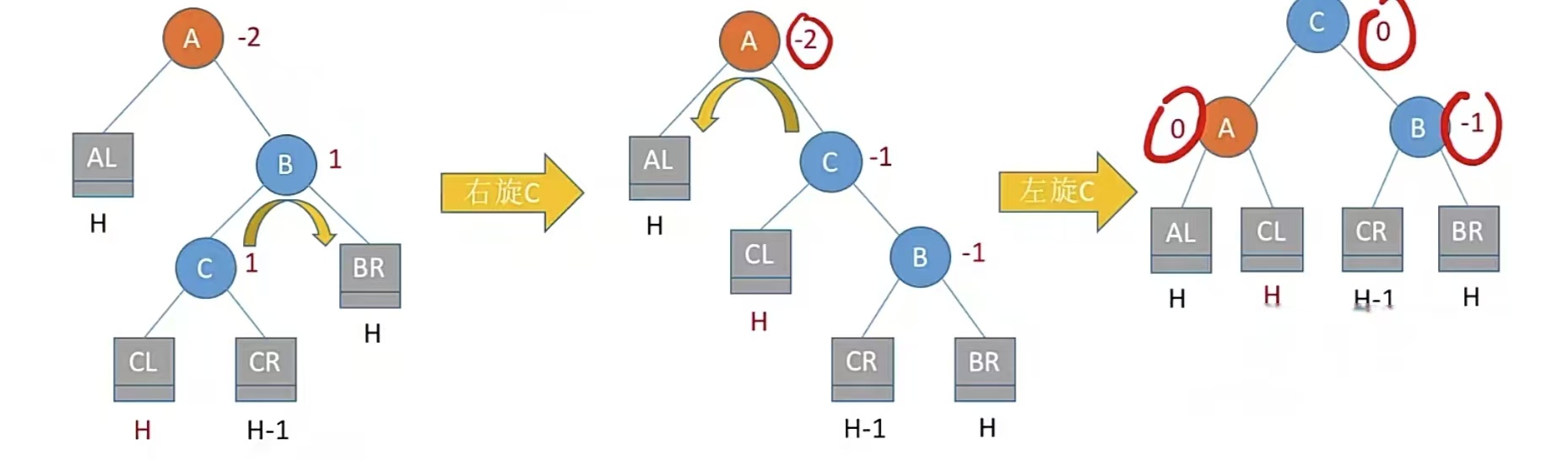
在这里插入图片描述

其实也是转了两次。先把C的右孩子变成B的左孩子，再让B变成C的右孩子，然后再让C的左孩子变成A的右孩子，再让A变成C的左孩子。

简单来说就是先让C到B的位置，再让C到A的位置。因为C是A右孩子的左孩子，所以C到B要右旋，再到A要左旋，就是这样，没别的。这样旋转过后，还是满足AL<A<CL<C<CR<B<BR，符合二叉排序树且平衡。

我们假设的是C的右子树高度为H-1，左子树高度为H（新结点插到C的左子树上），其实C的右子树高度为H，左子树高度为H-1也是一样的转（新结点插到了右子树上），也没什么区别。

其实综合来看，我们会发现，只有右孩子才能左上旋，只有左孩子才能右上旋，所以只要我们看转的那个是左孩子还是右孩子也能顺出来。

在插入操作中，只要将最小不平衡子树调整平衡，则其他祖先节点都会恢复平衡。

2.插入的查找效率分析

显然我们知道，若树高为h，则最坏情况下，查找一个关键字最多需要对比h次，即查找操作的时间复杂度（ASL）不可能超过O(h)。

还记得我们平衡二叉树的定义吗？平衡二叉树——树上任一结点的左子树和右子树的高度之差不超过1，所以它有一些性质，我们假设以nh表示深度为h的平衡树中含有的最少结点数，则：

有n0 = 0，n1 = 1，n2 = 2，并且有nh = nh-1 + nh-2 + 1

怎么说？我们来看一下就知道了：当n为0的时候，高度为0，这是一棵空树；当n为1的时候，高度为1，这棵树最少只有一个节点；当n为2的时候，高度为2，这棵树最少只有一个根节点和它的左孩子/右孩子……我们n为h的时候，高度为h，这棵树最少就是左子树和右子树分别为h-1和h-2（因为根节点也占个高度），所以 nh = nh-1 + nh-2 + 1 。

可以证明含有n个结点的平衡二叉树的最大深度为O(log2n)，平衡二叉树的平均查找长度为O(log2n)。

这个证明的过程是个论文，有兴趣的可以自己看下哈。这个论文证明了含有n个结点的平衡二叉树的最大深度为O(log2n)，式子还挺复杂的，果然计算机的尽头是数学，数学的尽头是玄学（bu shi~）

3.删除

我们花了很大篇幅说平衡二叉树的插入操作是怎么回事，那么平衡二叉树的删除操作和它有什么共同点呢？

平衡二叉树的插入操作：

  • 插入新结点后，要保持二叉排序树的特性不变（左＜中＜右）；
  • 若插入新结点导致不平衡，则需要调整平衡。

平衡二叉树的删除操作：

  • 删除结点后，要保持二叉排序树的特性不变（左＜中＜右）；
  • 若删除结点导致不平衡，则需要调整平衡。

其实都是操作后要保持二叉排序树的特性，且要调增平衡。

删除说白了其实就是先把这个结点按照二叉排序树的方式给删了，然后再往上找到最小不平衡子树给它调整平衡，完了如果发现上面的还不平衡就再往上找最小不平衡子树给它调整平衡，就是这样。我们来看看具体是怎么操作的：

平衡二叉树的删除操作具体步骤：

  1. 删除结点（方法同“二叉排序树”）；

  2. 一路向北找到最小不平衡子树，找不到就结束；

  3. 找最小不平衡子树下，“个头”最高的儿子、孙子；

  4. 根据孙子的位置，调整平衡（LL/RR/LR/RL）；

  5. 如果不平衡向上传导，继续第2条。

其中的第① 、④、⑤需要细说：

① 删除结点（方法同“二叉排序树”）：

  • 若结点的删除是叶子结点，直接删；
  • 若删除的结点只有一个子树，用子树顶替删除位置；
  • 若删除的结点有两棵子树，用前驱（或后继）结点顶替，并转换为对前驱（或后继）结点的删除。

④ 根据孙子的位置，调整平衡（LL/RR/LR/RL）；

  • 孙子在LL：儿子右单旋；
  • 孙子在RR：儿子左单旋；
  • 孙子在LR：孙子先左旋，再右旋；
  • 孙子在RL：孙子先右旋，再左旋；

⑤ 如果不平衡向上传导，继续第2条。

  • 对最小不平衡子树的旋转可能导致树变矮，从而导致上层祖先不平衡，不平衡向上传递。

什么意思呢？别急，看几个栗子就明白了：

⑴ 例1
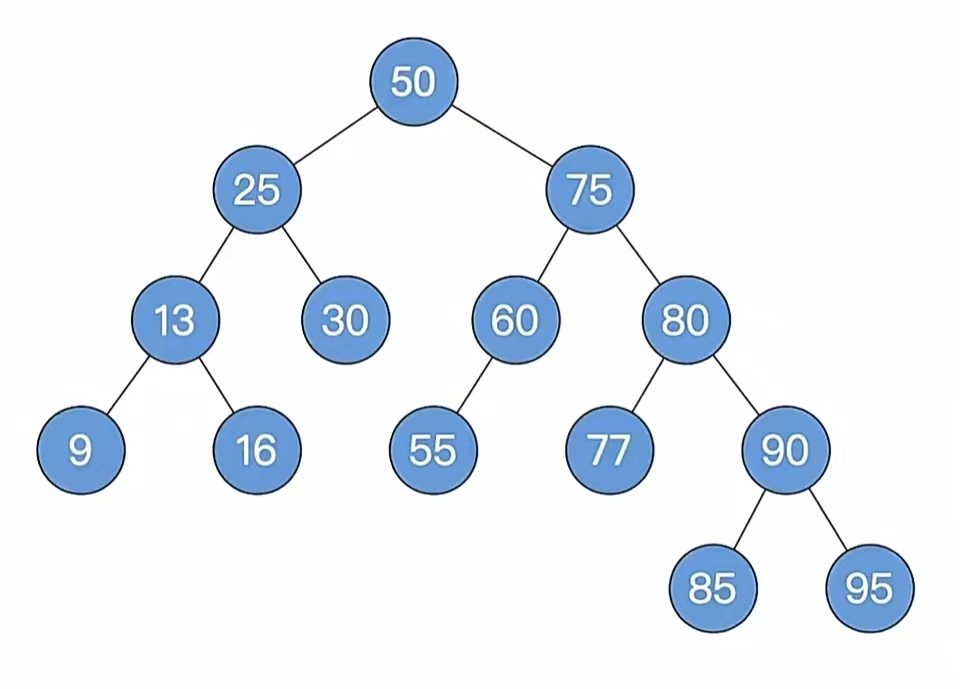
在这里插入图片描述

这是一棵平平无奇的二叉排序树，现在我们要删掉最左下的结点“9”

那么我们看步骤1，删除和二叉排序树的删除一样的，“9”是叶子结点，直接删掉就好了，删掉后就是这个样子：

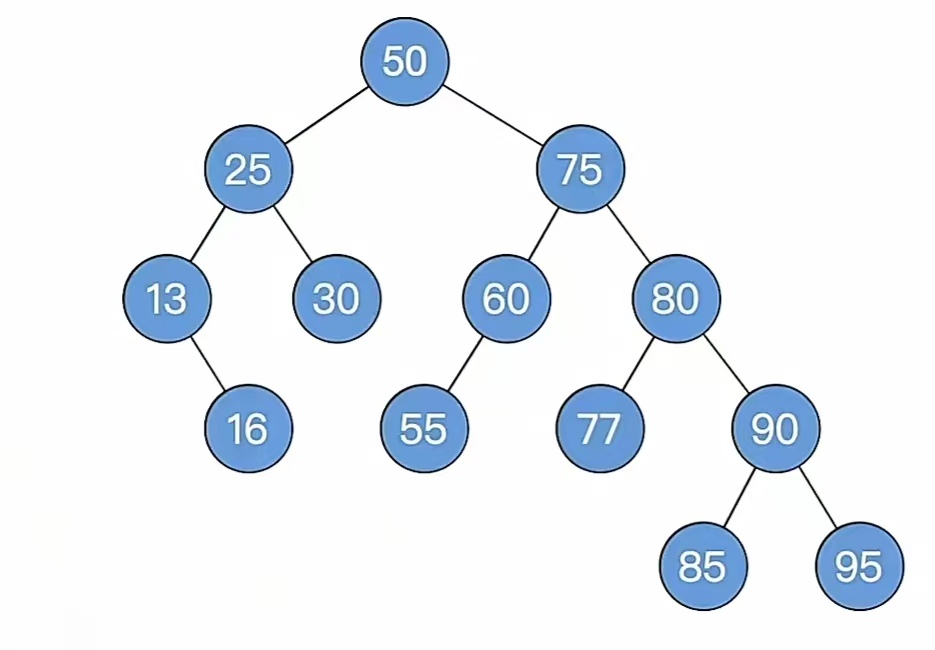
在这里插入图片描述

那么我们再看第步骤2，自底向上找最小不平衡子树，我们发现找不到，于是就完成了该平衡二叉树的指定结点删除。

⑵ 例2

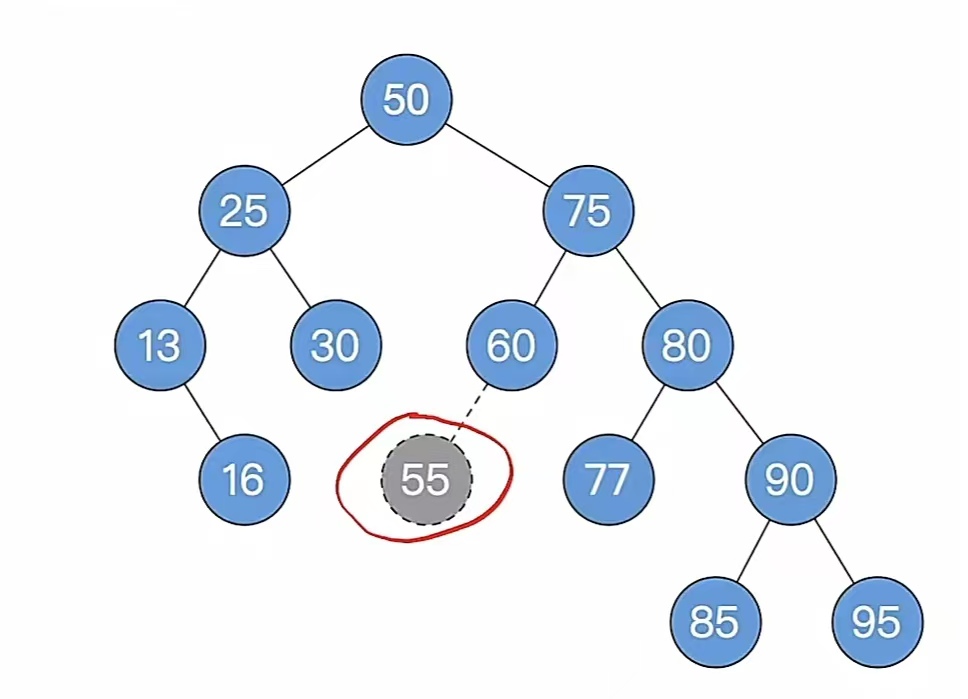
在这里插入图片描述

介个平衡二叉树，我们要把结点“55”给删了。看步骤1，删除按照二叉排序树的删除来删，我们发现它是叶子结点，所以直接删除。但是！！！和例1不同的是，我们走到步骤2，自底向上找最小不平衡子树，我们发现它不平衡了，这个最小不平衡子树就是以“75”为根的根节点。

那么发现不平衡了我们该怎么办？走到步骤3，找最小不平衡子树下，“个头”最高的儿子、孙子，那么我们来找一下：

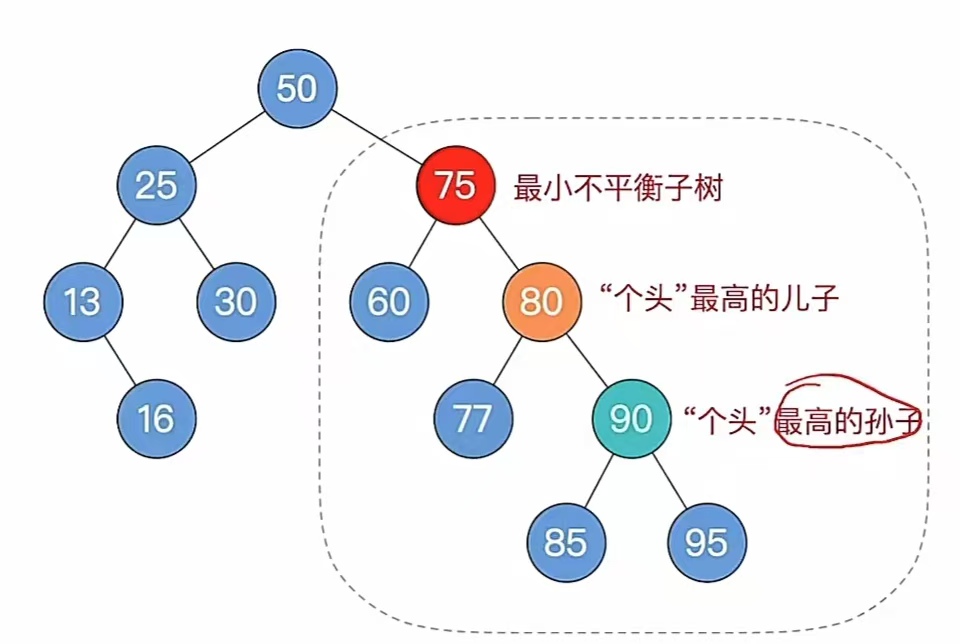
在这里插入图片描述

现在我们已经找到了最小不平衡子树下，“个头”最高的儿子、孙子，可以开始**步骤4，根据孙子的位置，调整平衡（LL/RR/LR/RL）**了。这是啥意思呢？其实我们在说步骤的时候也细说了，步骤4是这个意思：

④ 根据孙子的位置，调整平衡（LL/RR/LR/RL）；

  • 孙子在LL：儿子右单旋；
  • 孙子在RR：儿子左单旋；
  • 孙子在LR：孙子先左旋，再右旋；
  • 孙子在RL：孙子先右旋，再左旋；

其实就是和刚刚说的插入一样的，就是把“个头”最高的孙子当做是“插入”的结点一样对待，然后再看它是LL，RR，还是LR，RL，如果是LL，RR就儿子右旋/左旋，如果是LR就孙子先左再右（LR型嘛，先L再R），RL就孙子先右再左（RL型嘛，先R再L），就可以了

显然这是“LL”型，所以我们进行左单旋，也就是这样：

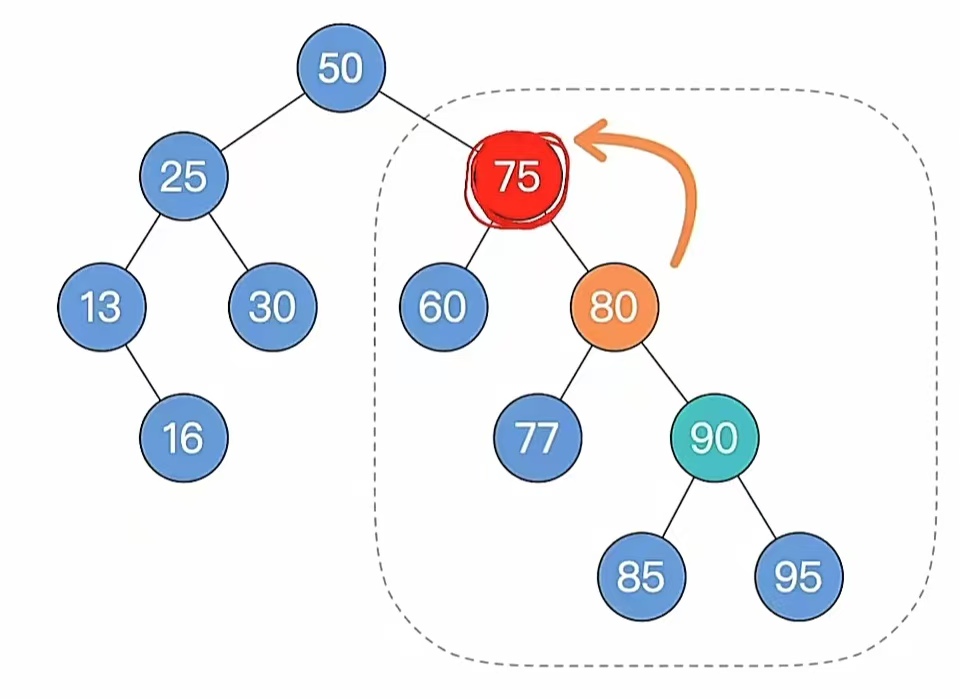
在这里插入图片描述
旋转后结果如下：

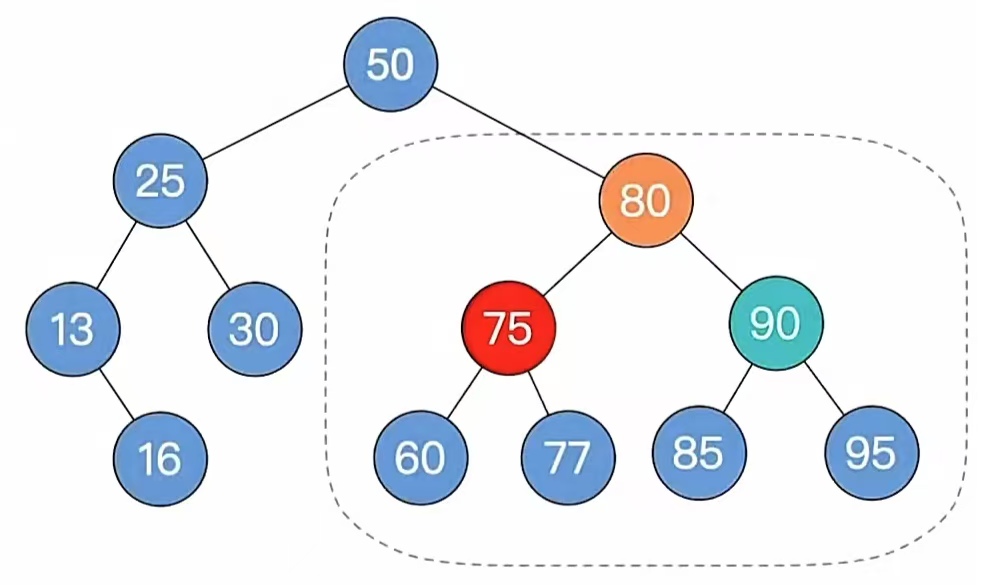
在这里插入图片描述
此时我们来到步骤5，如果不平衡向上传导，继续第2条，那我们这个时候会发现，它已经平衡了，不平衡没有向上传导，所以我们删除完成。

⑶ 例3

再看个例子：

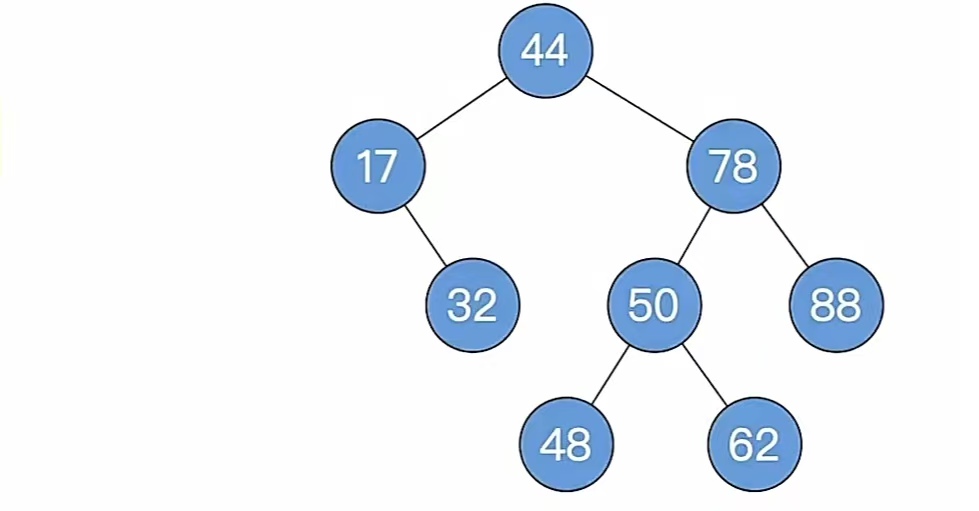
在这里插入图片描述

这个平衡二叉树，我们现在要删除“32”结点。当然还是按照步骤走，先按照二叉排序树那样删，完了再看看平不平衡，平衡就vans不平衡就找到最小不平衡树给它调整平衡，再看看调整完平不平衡，不平衡再给它调整平衡。

那我们看步骤1，删除和二叉排序树的删除一样的，“9”是叶子结点，直接删掉就好了，删掉后再看步骤2，自底向上找最小不平衡子树，删掉后发现不平衡了，找最小不平衡子树：

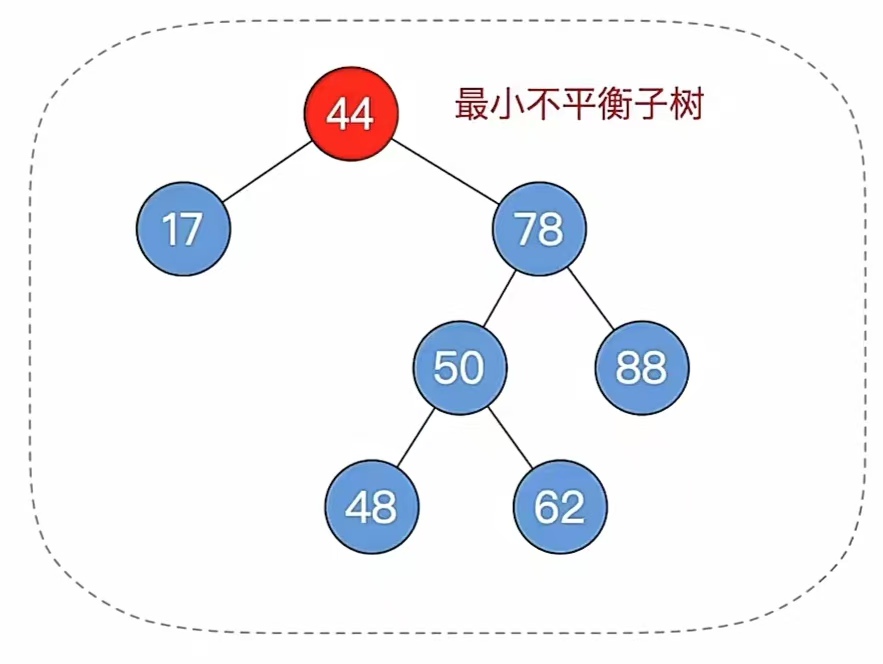
在这里插入图片描述
发现不平衡了我们该调整平衡。走到步骤3，找最小不平衡子树下，“个头”最高的儿子、孙子，我们会发现“个头”最高的儿子、孙子分别是“78”，“50”，还记得发现后怎么办吗？把孙子当做插入的结点来调整，我们发现是“RL”型，孙子先右旋再左旋

其实这样也是走到了步骤4，根据孙子的位置，调整平衡（LL/RR/LR/RL），也就是就这样：

④ 根据孙子的位置，调整平衡（LL/RR/LR/RL）；

  • 孙子在LL：儿子右单旋；
  • 孙子在RR：儿子左单旋；
  • 孙子在LR：孙子先左旋，再右旋；
  • 孙子在RL：孙子先右旋，再左旋；

如下图：

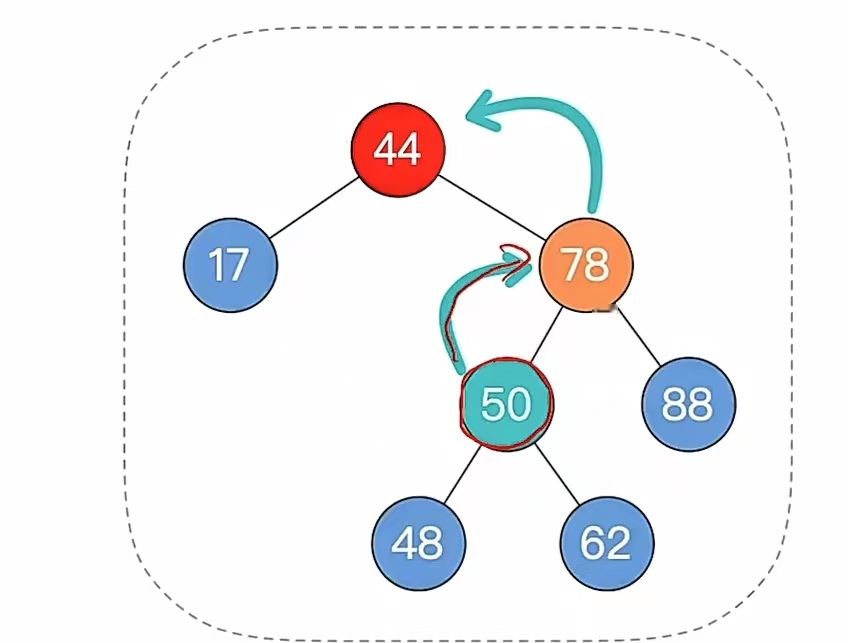
在这里插入图片描述

调整后就是这样：

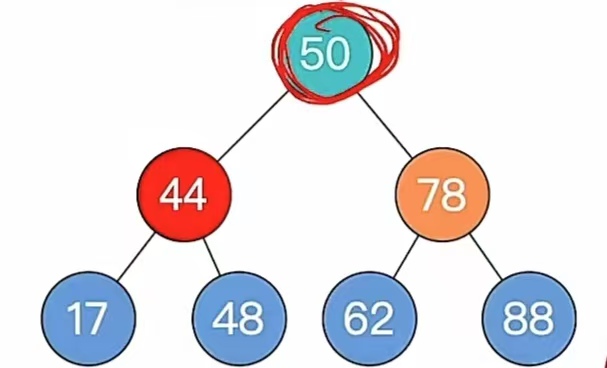
在这里插入图片描述

我们再看步骤5，如果不平衡向上传导，继续第2条，那我们这个时候会发现，它已经平衡了，不平衡没有向上传导，所以我们删除完成。

⑷ 例4

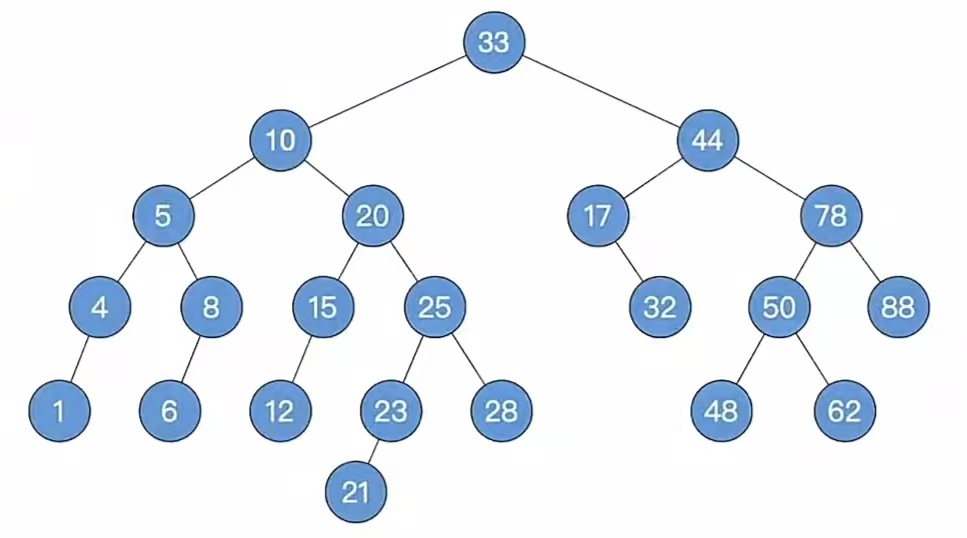
在这里插入图片描述
这次我们删除结点“32”，还是按照老办法，二叉排序树删除，发现是叶结点，直接删除；然后再自底向上找最小不平衡子树，如下：

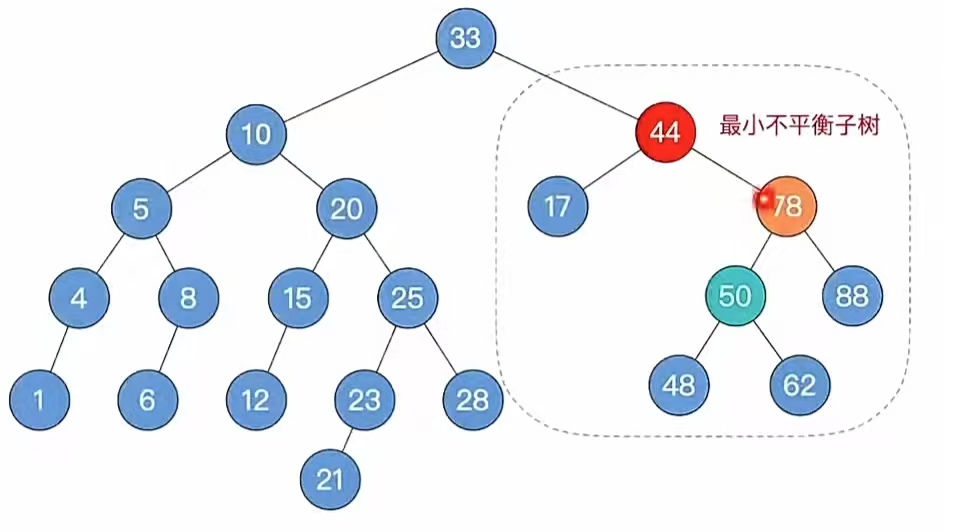
在这里插入图片描述

此时“个头”最高的儿子、孙子分别是“78”，“50”，再根据孙子的位置调整平衡，我们发现是“RL”型，调整如下：

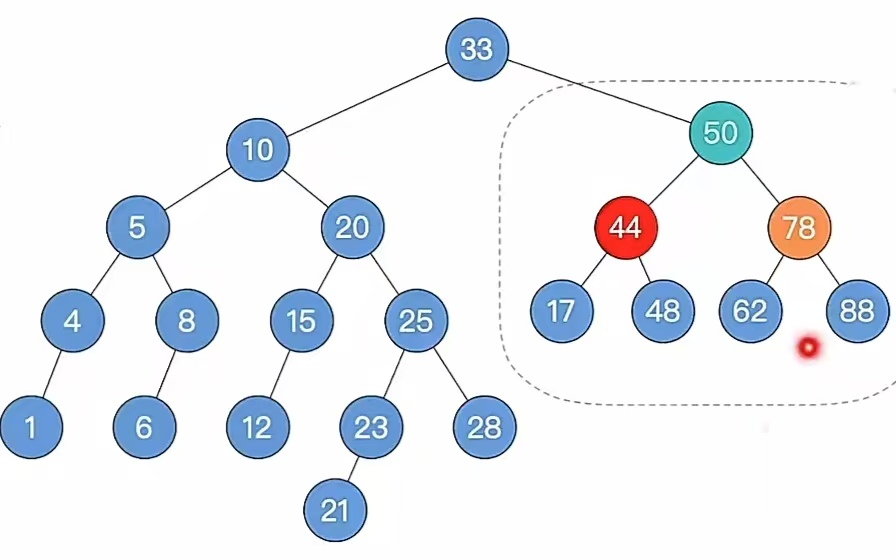
在这里插入图片描述

好，注意！！！此时我们来到步骤5，如果不平衡向上传导，继续第2条：

⑤ 如果不平衡向上传导，继续第2条。

  • 对最小不平衡子树的旋转可能导致树变矮，从而导致上层祖先不平衡，不平衡向上传递。

我们自底向上找，发现确实不平衡向上传递了，于是我们回到步骤2，自底向上找最小不平衡子树，我们找到最小不平衡子树是整棵树；于是来到步骤3，找最小不平衡子树下，“个头”最高的儿子、孙子，我们找到如下：

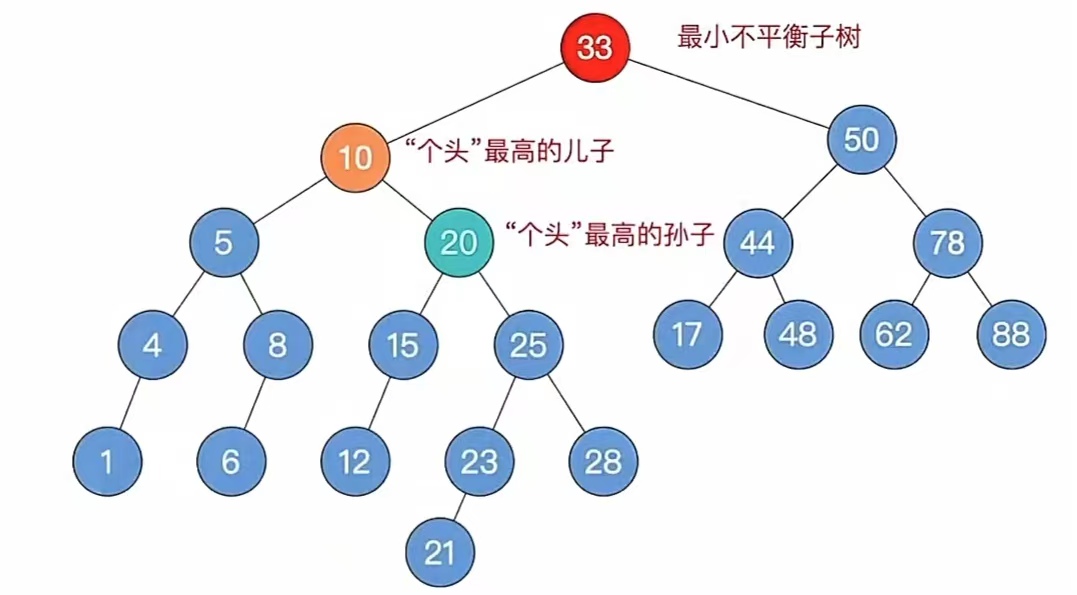
在这里插入图片描述

此时又来到步骤4，根据孙子的位置，调整平衡（LL/RR/LR/RL）， 我们发现孙子是“LR”型，所以先左旋再右旋：

左旋：
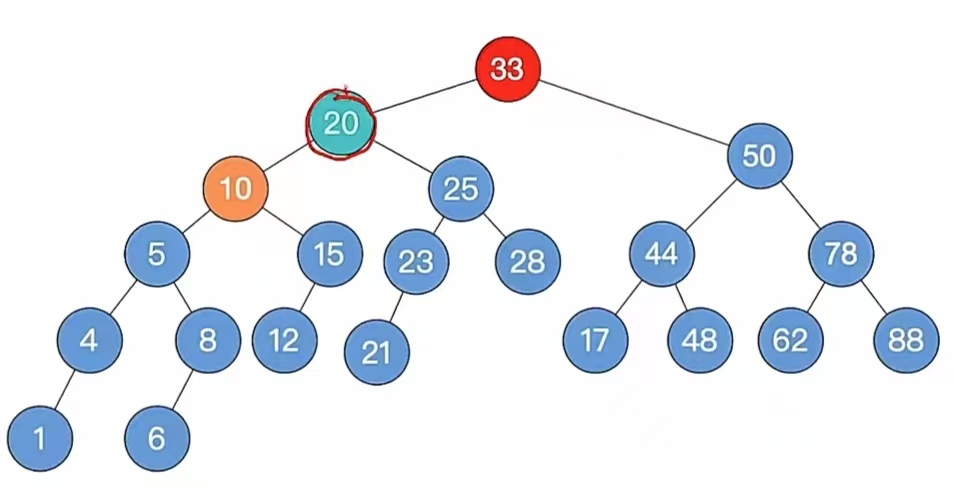
在这里插入图片描述
右旋：

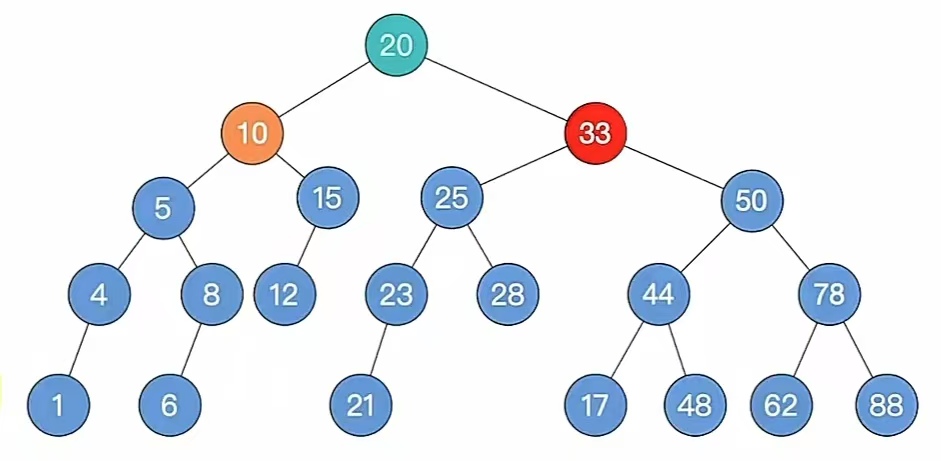
在这里插入图片描述

此时又双叒叕来到步骤5，如果不平衡向上传导，继续第2条，那我们这个时候会发现，它已经平衡了，不平衡没有向上传导，所以我们删除完成。

⑸ 例5

我们一直删的都是叶子结点，这次我们不删叶子结点，我们删除结点“75”：
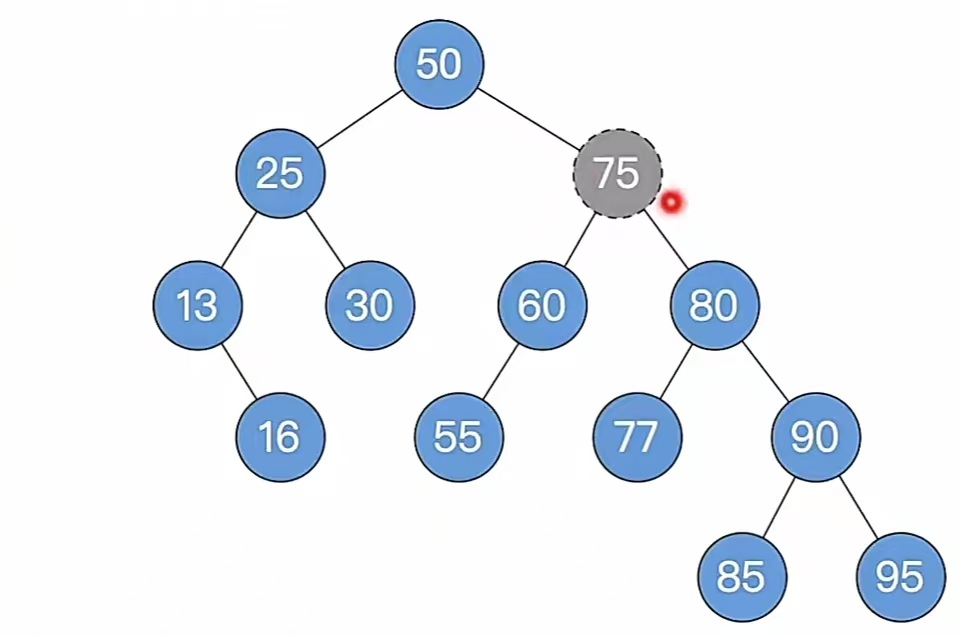
在这里插入图片描述
我们步骤1，删除和二叉排序树一样删就好了，也就是这样：

① 删除结点（方法同“二叉排序树”）：

  • 若结点的删除是叶子结点，直接删；
  • 若删除的结点只有一个子树，用子树顶替删除位置；
  • 若删除的结点有两棵子树，用前驱（或后继）结点顶替，并转换为对前驱（或后继）结点的删除。

用前驱或后继代替，前驱是“60”，后继是“77”，我们先用前驱顶替，也就是用“60”来。我们怎么顶替？也就是上面说的删除结点第3条：

被删除结点有左右子树，用前驱结点（或后继）顶替（复制数据即可），并转化为对前驱（或后继）结点的删除

也就是说，我们把“60”复制到删除的那个结点的值，转化为删除“60”：
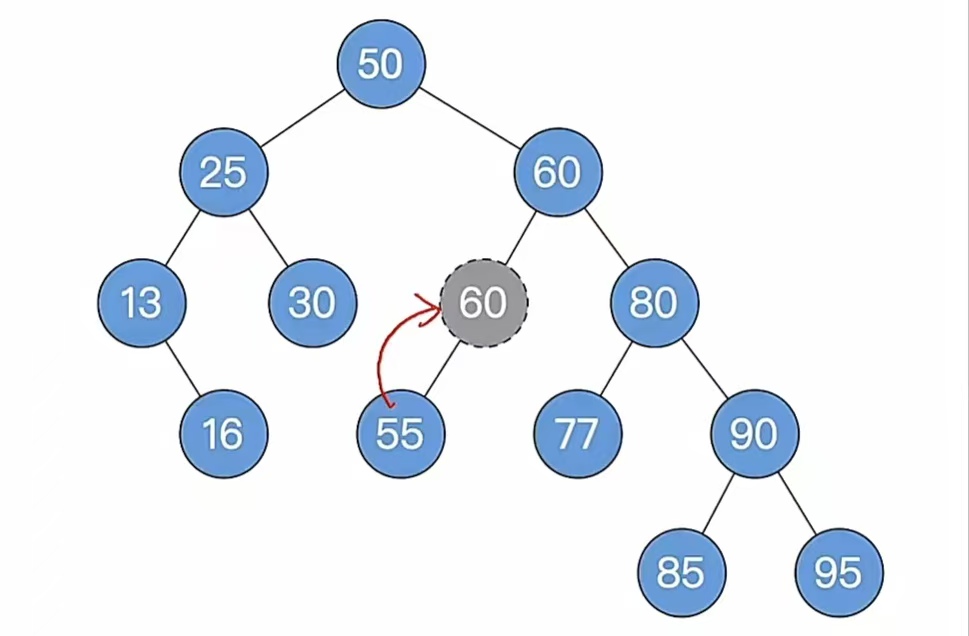
在这里插入图片描述

但是“60”也不是叶结点，所以还是要用前驱/后继顶替，但是！！！它并不是左右子树都有，只有一棵子树怎么办呢？也就是上面说的删除结点第2条：

被删除结点只有一个子树，所以用子树顶替删除位置（用结点实体顶替）

所以我们用结点“55”直接顶替。

顶替后来到步骤2，自底向上找最小不平衡子树，我们找到最小不平衡子树如下：

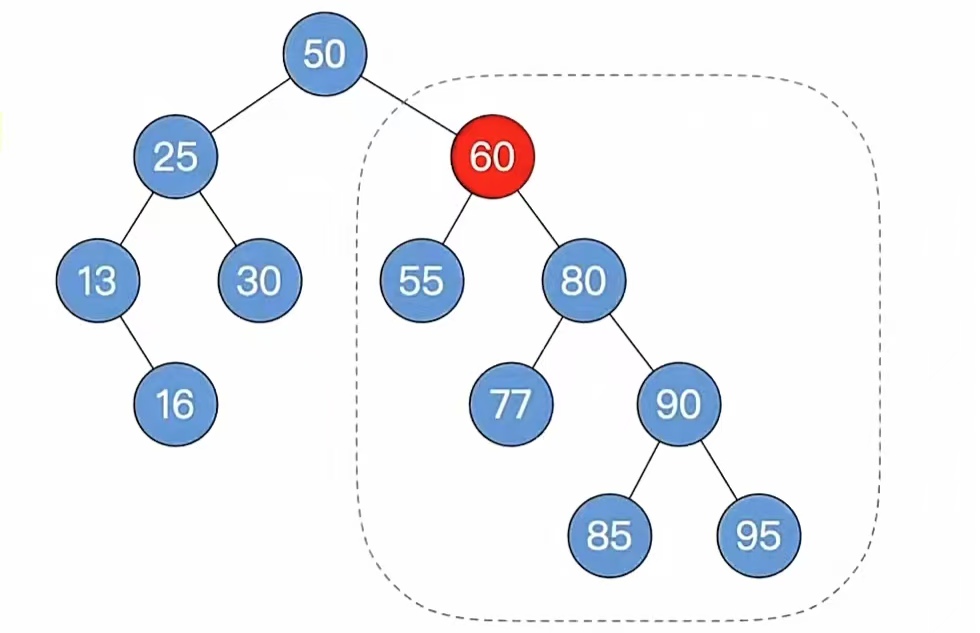
在这里插入图片描述

此时我们来到步骤3，找最小不平衡子树下，“个头”最高的儿子、孙子，找到分别为“80”，“90”，步骤4，根据孙子的位置，调整平衡（LL/RR/LR/RL）， 发现是“RR”型，我们对儿子进行左单旋：

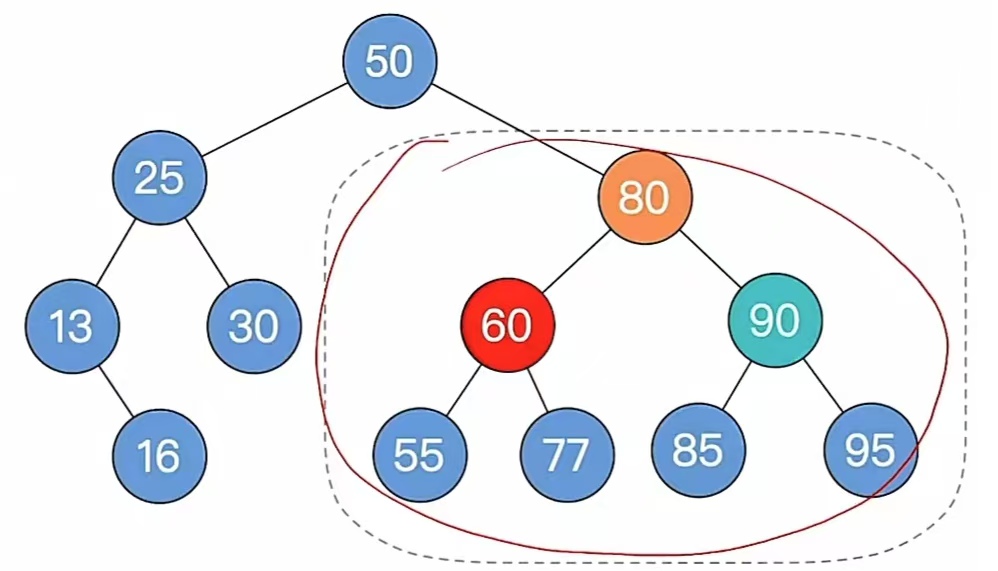
在这里插入图片描述
最后又是步骤5，如果不平衡向上传导，继续第2条，那我们这个时候会发现，它已经平衡了，不平衡没有向上传导，所以我们删除完成。

⑹ 例6

我们刚刚“例5”删结点“75”的时候用前驱顶替，现在我们用“后继”顶替，上面还得往上翻不太好看，这里再放一张：

在这里插入图片描述
① 删除结点（方法同“二叉排序树”）：

  • 若结点的删除是叶子结点，直接删；
  • 若删除的结点只有一个子树，用子树顶替删除位置；
  • 若删除的结点有两棵子树，用前驱（或后继）结点顶替，并转换为对前驱（或后继）结点的删除。

我们结点“75”可是左右子树都有的，也就是上面说的删除结点第3条：

被删除结点有左右子树，用前驱结点（或后继）顶替（复制数据即可），并转化为对前驱（或后继）结点的删除

我们发现后继是“77”，也就是说，我们把“77”复制到删除的那个结点的值，转化为删除“77”：

在这里插入图片描述

现在要删除的是叶结点，也就是上面说的删除结点第1条，所以直接删即可。

删除后来到步骤2，自底向上找最小不平衡子树，我们找到最小不平衡子树如下：
在这里插入图片描述

我们接下来应该来到步骤3，找最小不平衡子树下，“个头”最高的儿子、孙子，如下：

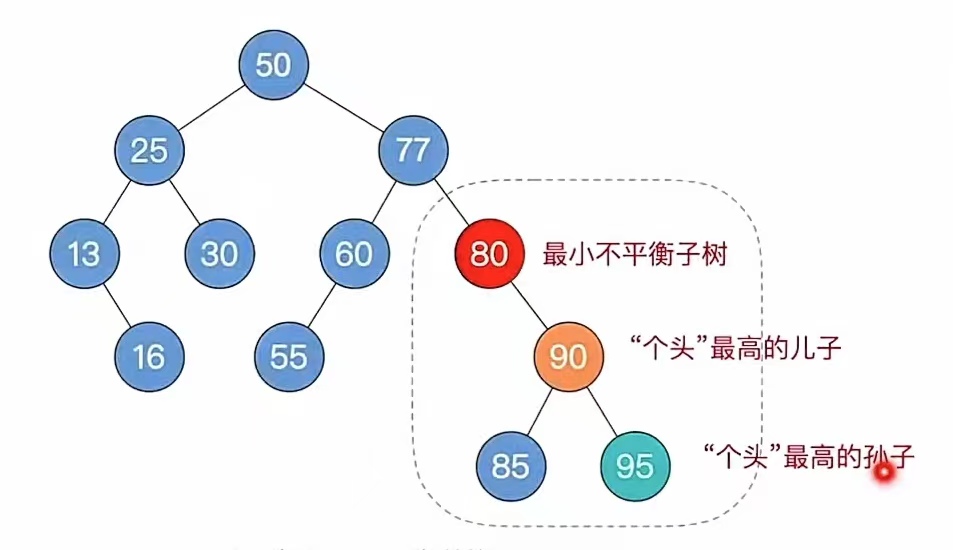
在这里插入图片描述

我们发现两个孙子“85”，“95”一样高，我们先把“95”当做“个头”最高的孙子（马上再说把“85”当做个头最高的孙子的情况）

现在就是**步骤4，根据孙子的位置，调整平衡（LL/RR/LR/RL）**我们发现是“RR”型，我们把孙子进行左单旋，调整后如下：

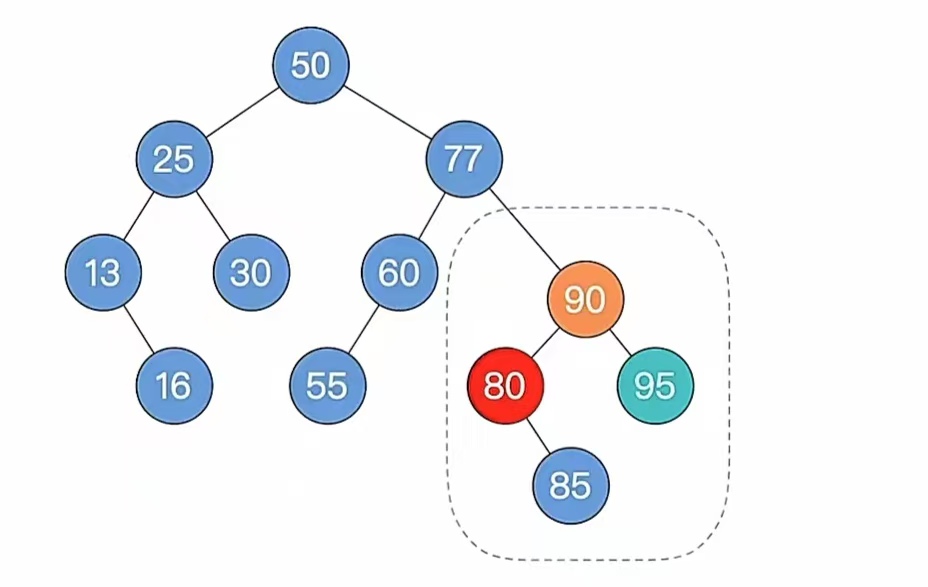
在这里插入图片描述

最后又是步骤5，如果不平衡向上传导，继续第2条，那我们这个时候会发现，它已经平衡了，不平衡没有向上传导，所以我们删除完成。

现在再拐回来说刚刚两个孙子一样高的时候的第二种情况，我们先把“95”当做“个头”最高的孙子：

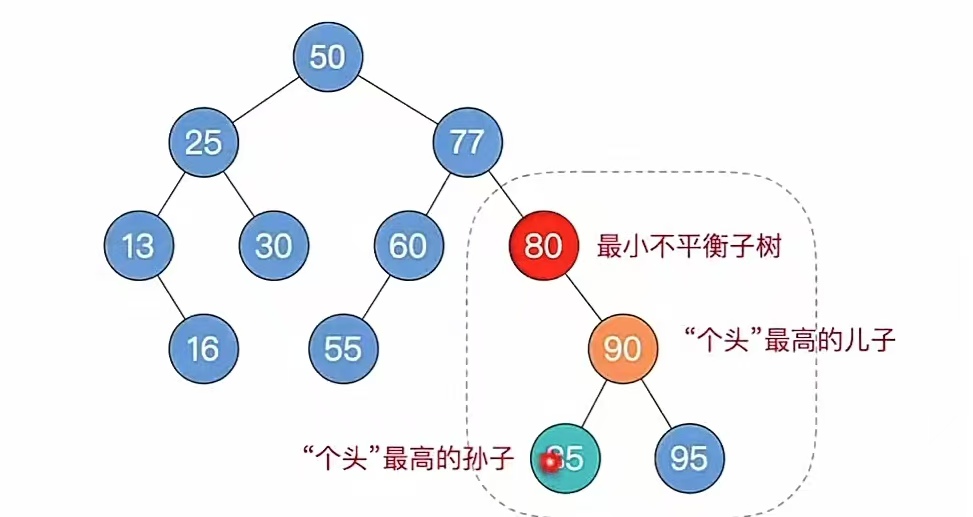
此时步骤4，根据孙子的位置，调整平衡（LL/RR/LR/RL），我们的孙子是“RL”型，要把孙子先右旋再左旋。

右旋：
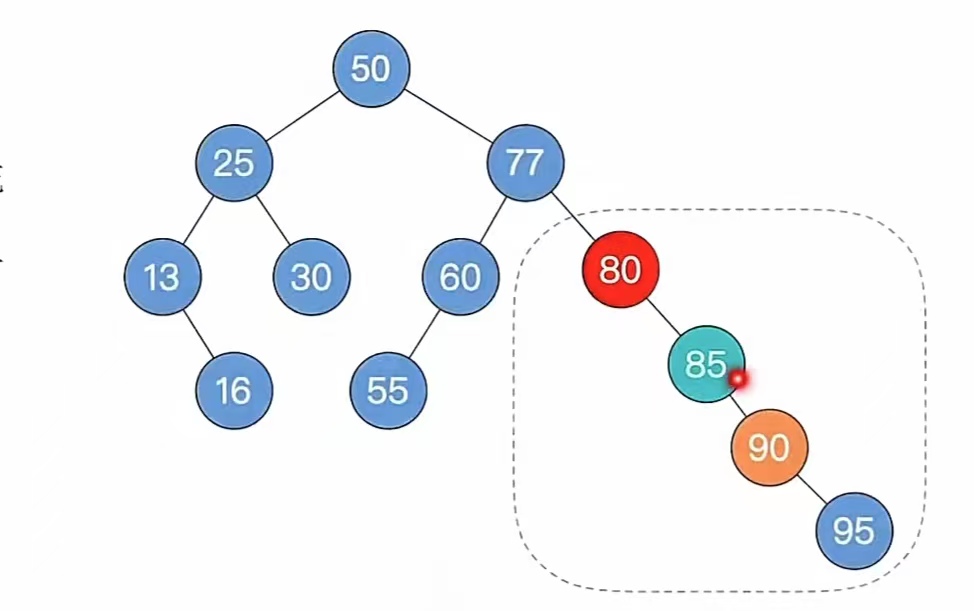
在这里插入图片描述

左旋：

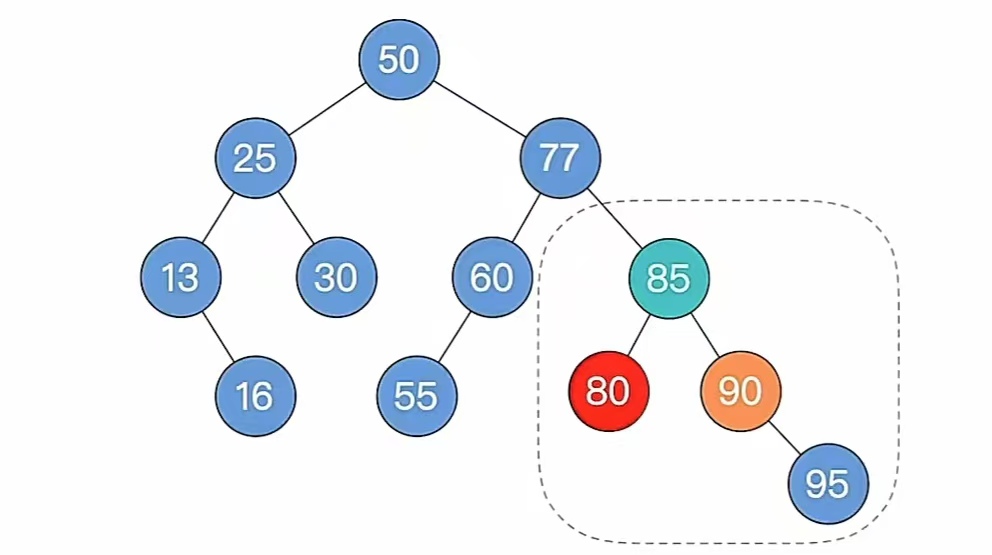
在这里插入图片描述
还是步骤5，如果不平衡向上传导，继续第2条，那我们这个时候会发现，它已经平衡了，不平衡没有向上传导，所以我们删除完成。

平衡二叉树删除的时间复杂度为O(log2n)

以上6个栗子，123是主要的，4也可以一看，56看不看都行~

总结

主要讲了BST和AVL，终点还是平衡二叉树的插入。平衡二叉树的插入，看平衡二叉树是哪种类型，LL，RR还是LR，RL，如果是LL，RR，就转A的左孩子/右孩子，如果是LR，就转A的孙子，先左旋再右旋（LR型嘛，先L再R），如果是RL，也转A的孙子，先右旋再左旋（RL型嘛，先R再L），注意如果是LL、RR针对的是儿子转，LR，RL针对的就是孙子转。还有就是要记得，平衡二叉树的最大深度为O(log2n)，平衡二叉树的平均查找长度/查找的时间复杂度为O(log2n)，平衡二叉树删除的时间复杂度为O(log2n)。

相关文章：

  • 【LeetCode 热题 100】全排列 / 子集 / 组合总和 / 分割回文串 / N 皇后
  • 论文阅读笔记——双流网络
  • 利用vba替换word中多个表格，相邻单元格的文字
  • 【Lua】Redis 自增并设置有效期
  • spring-cloud-stream学习
  • Halcon案例(二):C#联合Halcon回形针以及方向
  • 【idea】调试篇 idea调试技巧合集
  • 第五部分：第二节 - Node.js 核心模块：厨房里的基本工具
  • 显示的图标跟UI界面对应不上。
  • 无人机数据处理与特征提取技术分析！
  • Thrust库中的Gather和Scatter操作
  • 【Linux】第十六章 分析和存储日志
  • uniapp vue 沉浸式窗体如何获取并排除外部手机浏览器底部菜单栏工具栏高度
  • sqli—labs第六关——双引号报错注入
  • 小白学习java第18天（上）：spring
  • 【C++】17. 多态
  • 大型企业数据治理与数据资产化：数字化转型的炼金术革命
  • 如何解决电脑蓝屏错误代码：Oxc0000098
  • 鸿蒙OSUniApp开发支持多语言的国际化组件#三方框架 #Uniapp
  • elementUI调整滚动条高度后与固定列冲突问题解决
  • 微软将裁员3%，减少管理层
  • 美国和沙特签署上千亿美元军售协议
  • 俄副外长：俄美两国将举行双边谈判
  • 科普｜揭秘女性压力性尿失禁的真相
  • 人民日报访巴西总统卢拉：“巴中关系正处于历史最好时期”
  • 复旦相辉堂上演原创历史人物剧《王淑贞》，胡歌参演