当前位置：首页 > news >正文

19、HashTable（哈希）、位图的实现和布隆过滤器的介绍

news 来源：原创 2025/5/10 8:08:32

一、了解哈希【散列表】

1、哈希的结构

在这里插入图片描述

在STL中，HashTable是一个重要的底层数据结构, 无序关联容器包括unordered_set, unordered_map内部都是基于哈希表实现
- 哈希表又称散列表，一种以「key-value」形式存储数据的数据结构。
- 哈希函数：负责将任意大小的输入映射到固定大小的输出，即哈希值。
  - 这个哈希值作用：是放在在数组中存储键值对的索引。
- 哈希冲突：由于哈希函数的映射不是一对一的，可能会出现两个不同的键映射到相同的索引，即冲突。

解决冲突的方法：
链地址法
开发寻址法
双重哈希

2、哈希函数

定义：将键（任意类型）映射为固定大小的整数（哈希值），决定数据在哈希桶中的存储位置。

可能出现的情况
冲突情况 ：将两个或两个以上的不同key映射到同一地址。

3、hash操作

插入
查找

4、哈希的负载因子【重点】

负载因子 = 存储的元素个数/数组长度
用来形容散列表的存储密度
负载因子越小，冲突越小，负载因子越大，冲突越大。
描述冲突的程度。

5、哈希冲突的解决方法

5.1、链地址法

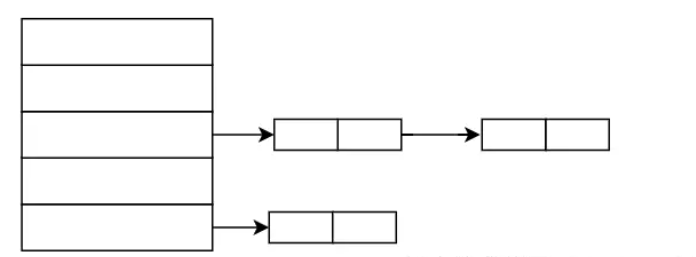
在这里插入图片描述
方法一：拉链法（链表法）将具有相同的addr的key，可以用链表连接。但是负载因子要在合理范围内。

5.2、开发寻址法

方法二：开发寻址法

将所有的数据直接存储在哈希数组中。如果冲突就采用某种算法来改变位置。
- 算法有多种思路：
- 比如 i+1，i+2，i+3等等或者 i^1, i ^ 2 , i ^3等等。但是他们会出现hash聚集，也就是近似值的hash值很接近，那么位置也接近。聚集的话，就会在一片区域内，查找，这片区域数据太多了，时间复杂从O（1）变O（n）。所以可以使用双重哈希解决。 但是负载因子要在合理范围内。

6、分布式一致性哈希

6.1、了解

一致性哈希通过环形哈希空间（Hash Ring）和 虚拟节点（Virtual Nodes）优化数据分布。

解决传统哈希表在节点数量变化时导致的全局数据迁移问题（例如模运算哈希的 hash(key) % N，当 N 变化时所有数据需重新分布）。
一致性哈希，当节点增删时，仅影响环上相邻节点的数据，避免全局数据迁移。

6.2、哈希环

将节点和数据通过哈希函数映射到一个环形空间（通常范围为 0 ~ 2^32 - 1）
节点和数据的位置由哈希值决定。

每个数据项沿环顺时针查找最近的节点作为存储位置。

6.3、基本原理

在这里插入图片描述

第一步：
- 创建哈希环。
- 将节点和数据通过哈希函数映射到一个环形空间
第二步：
- 将数据 a 、b 、c 通过哈希函数确定环上的位置，放上去。

在这里插入图片描述

第三步
- 确定a、b、c映射到哪一个节点上。
- 按顺时针顺序，将a、b、c映射到离它们最近的节点。

在这里插入图片描述

第四步
- 新增节点4，放在 1和2之间：仅需将环上相邻节点的部分数据迁移到新节点。

在这里插入图片描述

第五步
- 删除节点 4 ，把节点4上的数据 a 迁移到节点2上
- - 移除节点：该节点的数据顺时针迁移到下一个相邻节点。

6.4、虚拟节点

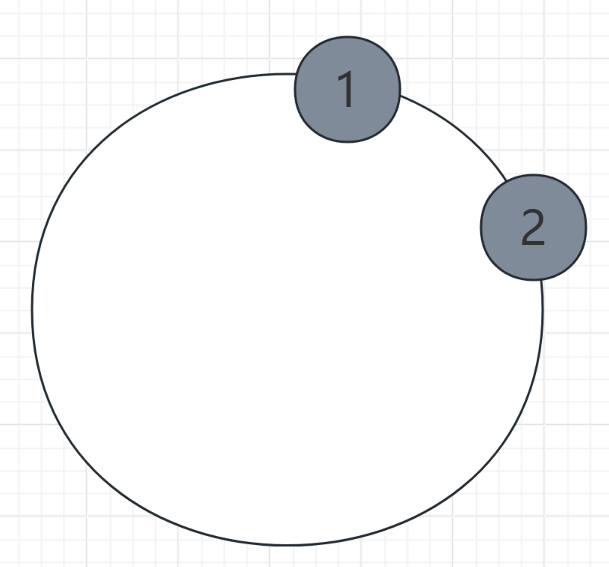
在这里插入图片描述

问题：
- 若物理节点较少，数据可能分布不均【哈希偏移】, 如上图。
- 哈希偏移:
  - 在一致性哈希中，如果节点数量较少，可能会导致数据分布不均匀，某些节点负载过高，而其他节点负载较低。
解决：
- 每个物理节点映射多个虚拟节点 。
- 数据最终存储在虚拟节点对应的物理节点。

虚拟节点的优点

数据分布均匀
虚拟节点将物理节点的负载分散到哈希环的多个位置，避免数据倾斜。

动态扩容
增加物理节点时，只需为其分配虚拟节点，数据迁移量较少。

容错性
删除物理节点时，其虚拟节点对应的数据会迁移到其他物理节点，系统仍然保持平衡。

7、哈希的代码

#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<sstream>
#include<vector>
#include<functional>
#include<utility>
#include<list>
#include<string>
#include<iostream>
#include<algorithm>
using namespace std;
template<class Key,class Value,class Hash=hash<Key>>
class HashTable{class HashNode{public:Key key;Value value;//从key构造节点，Value使用默认构造explicit HashNode(const Key& key):key(key),value(){}//从key和value构造节点HashNode(const Key&key,const Value& value):key(key),value(value){}//比较运算符，只按key来比较bool operator==(const HashNode& other)const{return key==other.key;}bool operator!=(const HashNode& other)const{return key!=other.key;}bool operator<(const HashNode& other)const{return key<other.key;}bool operator>(const HashNode& other)const{return key>other.key;}bool operator==(const Key& key)const{return this->key==key;}//打印void print ()const{cout<<key<<" "<<value<<" ";}};private:using Bucket = list<HashNode>;//定义桶的类型为存储键的链表vector<Bucket> buckets;       //存储所有桶的动态数组size_t tableSize;             //哈希表的大小，即桶的数量size_t numElements;           //哈希中的元素的数量float maxLoadFator = 0.75;    //默认最大负载因子Hash hashFunction;            //哈希函数对象//计算哈希值，并将其映射到桶的索引size_t hash(const Key& key)const{return hashFunction(key) % tableSize;}//当元素数量超过最大负载因子定义的容量时，增加桶的数量并重新分配所有键void rehash(size_t newSize){vector<Bucket> newBucket(newSize);//创建新的桶组for(Bucket& bucket:buckets){//遍历旧桶//遍历桶中的每一个键for(HashNode& hashNode:bucket){//因为这里是新的newSize计算，所以不能用hash(key)来求size_t newIndex=hashFunction(hashNode.key)%newSize;newBucket[newIndex].push_back(hashNode);//将键重新放入桶中}}buckets = move(newBucket);//使用移动语义更新桶数组tableSize = newSize;}
public://构造函数初始化哈希表HashTable(size_t size = 10,const Hash& hashFunc = Hash()):buckets(size),hashFunction(hashFunc),tableSize(size),numElements(0){}//插入键到哈希表中void insert(const Key&key,const Value& value){if((numElements+1)>maxLoadFator*tableSize){//检查是否需要重哈希//处理clear后再次插入元素时，tableSize = 0 的情况if(tableSize==0)tableSize = 1;rehash(tableSize*2);// 重哈希，桶数量翻倍}size_t index = hash(key);    //计算键的索引list<HashNode>& bucket = buckets[index];//获取对应的桶//如果不在桶中，则添加到桶中if(find(bucket.begin(),bucket.end(),key)==bucket.end()){bucket.push_back(HashNode(key,value));++numElements;}}void insertKey(const Key&key){insert(key,Value{});}//从哈希表中移除键void erase(const Key& key){size_t index = hash(key);//计算键的索引auto & bucket = buckets[index];//获取对应的桶auto it = find(bucket.begin(),bucket.end(),key);//查找键if(it!=bucket.end()){bucket.erase(it);//删除键numElements--;//减少元素的数量}}//查找键是否在哈希表中Value* findKey(const Key& key){size_t index = hash(key);//计算键的索引auto & bucket = buckets[index];//获取对应的桶auto it = find(bucket.begin(),bucket.end(),key);//查找键if(it!=bucket.end()){return &it->value;}return nullptr;}//获取哈希表中的元素数量size_t size()const {return numElements;}//打印哈希表中的所有元素void print()const{for(size_t i = 0;i<buckets.size();++i){for(const HashNode& element:buckets[i]){element.print();}}cout<<endl;}void clear(){this->buckets.clear();this->numElements=0;this->tableSize = 0;}
};
int main(int argc, char const *argv[])
{//创建一个哈希表实例HashTable<int, int> hashTable;int n;cin>>n;getchar();string line;for(int i = 0;i<n;i++){getline(cin,line);istringstream iss(line);string command;iss>>command;int key;int value;if(command=="insert"){iss>>key>>value;hashTable.insert(key,value);}if(command == "erase"){if(hashTable.size()==0){continue;}iss>>key;hashTable.erase(key);}if(command=="find"){if(hashTable.size()==0){cout<<"not exist"<<endl;continue;}iss>>key;int* res = hashTable.findKey(key);if(res!=nullptr){cout<<*res<<endl;}else{cout<<"not exist"<<endl;}}if(command=="print"){if(hashTable.size()==0){cout<<"empty"<<endl;}else{hashTable.print();}}if(command=="size"){cout<<hashTable.size()<<endl;}if(command=="clear"){hashTable.clear();}}return 0;
}

二、位图

1、问题一

腾讯问题：给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在40亿个数中。【哈希表：每个无符号整数占4字节。40亿占的是16G】

1 B是 8 bit 。
1GB = 1024MB。
1MB = 1024 KB 。
1KB = 1024B 。
40 亿个无符号整数是每个数 4字节。就有 160 亿字节
160亿字节/1024/1024/1024 ≈ 14.9 GB

2、介绍

创建一段数组空间，用比特 1 和 0 来表示存在和不存在（1是存在，0是不能存在）。

3、实现位图的计算

void set(size_t x) {size_t index = x / 32;  // 定位到哪个 intsize_t pos = x % 32;    // 定位到 int 的哪一位bits[index] |= (1 << pos);//更新pos位置的 1
}

例如 x = 37：
- index = 37 / 32 = 1（第 2 个 int）
  - 假设 bit[index]= 0000 0100
- pos = 37 % 32 = 5（第 5 位）
  - 得pos = 0001 0000
- bits[1] |= (1 << 5) 将第 37 位设为 1
- 0000 0100 | 0001 000 = 0001 0100 。保持了原来的位的1，并更新了现在要改的位为 1

3、操作

3.1、了解运算符

在这里插入图片描述

3.2、位图操作

在这里插入图片描述

4、位图的优缺点

查找很快
但是只能用于整型

5、代码实现

#include <cstddef>
#include<vector>
#include<iostream>
using namespace std;
namespace bit{class bitset{public:explicit bitset(size_t N){bits.resize(N/32+1,0);//如果是32的倍数，会多分配一个int}//设置位图void set(size_t x){size_t index = x/32;//算出x映射的位在第几个整型size_t pos = x%32;//算出x在这个整型的第几个位置bits[index]|= (1<<pos);//保留原来的1 ，设置现在需要 位 的1++num;}第pos个位置设置为0void reset(size_t x){size_t index = x/32;//算出x映射的位在第几个整型size_t pos = x%32;//算出x在这个整型的第几个位置bits[index] &= ~(1<<pos);//第pos个位置设置为0}//判断x在不在bool test(size_t x){size_t index = x/32;size_t pos = x%32;return bits[index]&(1<<pos);}private:vector<int> bits;size_t num;//个数};
};
void test_bitset(){using namespace bit;bitset bs(100);bs.set(99);bs.set(98);bs.set(97);for(size_t i =0;i<100;++i){cout<<"[%d]:%d\n"<<i<<static_cast<int>(bs.test(i))<<endl;}
}
int main(int argc, char const *argv[])
{test_bitset();return 0;
}