LLM 论文精读（三）Demystifying Long Chain-of-Thought Reasoning in LLMs

这是一篇2025年发表在arxiv中的LLM领域论文，主要描述了长思维链 Long Chain-of-Thought 对LLM的影响，以及其可能的生成机制。通过大量的消融实验证明了以下几点：

• 与shot CoT 相比，long CoT 的 SFT 可以扩展到更高的性能上限；
• 较长 CoT 的 SFT 相比于短的 CoT 而言进一步改进 RL 变得更容易；
• SFT 初始化至关重要：高质量、涌现的long CoT 模式能够显著提高泛化能力和强化学习的收益；
• CoT 的长度并不总是以稳定的方式增加；
• 构建奖励函数可以用来稳定和控制CoT长度，同时提高准确率；
• 余弦奖励可以进行调整，以激励各种长度扩展行为；
• 模型可能需要更多训练样本来学习到如何利用更大的上下文窗口大小；
• 长度奖励将通过足够的计算进行破解，但可以使用重复惩罚来缓解；
• 不同类型的奖励和惩罚具有不同的最优折扣因子；
• 向 SFT 添加噪声但多样化的数据，可在不同任务之间实现均衡的性能；

作者在文章最后提到了LLM的“推理”能力的一个可能来源是：预训练数据中包含了人类论坛中问答对话的内容，所以作者认为基于海量互联网数据预训练得到的模型仍然有未被人类关注到的其他能力。

---

写在最前面

为了方便你的阅读，以下几点的注意事项请务必了解：

• 该系列文章每个字都是我理解后自行翻译并写上去的，可能会存在笔误与理解错误，如果发现了希望读者能够在评论区指正，我会在第一时间修正错误。
• 阅读这个系列需要你有基本的 RL、DL 相关基础知识，有时候我会直接使用英文名词，因为这些词汇实在不容易找到符合语境的翻译。
• 原文可能因为版面限制存在图像表格与段落不同步的问题，为了更方便阅读，我会在博文中重新对图像表格进行排版，并做到引用图表的文字下方就能看到被引用的图表。因此可能会出现一张图片在博客中多处位置重复出现的情况。
• 对于原文中的图像，我会在必要时对图像描述进行翻译并附上我自己的理解，但如果图像描述不值得翻译我也不会强行写上去。

---

Basic Information

• 论文标题：Demystifying Long Chain-of-Thought Reasoning in LLMs
• 原文链接: https://arxiv.org/abs/2502.03373
• 发表时间：2025年02月05日
• 发表平台：arxiv
• 预印版本号：[v1] Wed, 5 Feb 2025 17:13:32 UTC (771 KB)
• 作者团队：Edward Yeo, Yuxuan Tong, Morry Niu, Graham Neubig, Xiang Yue
• 院校机构：
  • Tsinghua University;
  • Carnegie Mellon University;
• 项目链接: 【暂无】
• GitHub仓库: https://github.com/eddycmu/demystify-long-cot

---

Abstract

扩展推理计算可增强大型语言模型 (LLM) 的推理能力，而长思维链 (Long CoT) 可实现回溯和纠错等策略。强化学习 (RL) 已成为开发这些能力的重要方法，但Long CoT 出现的条件仍不清楚，并且 RL 训练需要谨慎的设计选择。本文中作者系统地研究了Long CoT 推理机制，确定了模型能够生成Long CoT 轨迹的关键因素。通过大量的监督微调 (SFT) 和 RL 实验，得出了四个主要发现：（1）虽然 SFT 并非绝对必要，但可以简化训练并提高效率；（2）推理能力往往会随着训练数据的增加而涌现，但发展方向并不能得到保证，因此奖励策略对于稳定 CoT 长度增长至关重要；（3）扩展可验证的奖励信号对于 RL 至关重要，利用带有噪声的网络提取解决方案并结合过滤机制，展现出强大的潜力，尤其适用于 STEM 推理等分布外 (OOD) 任务；(4)诸如纠错之类的核心能力本身就存在于基础模型中，但要通过强化学习有效地激励这些技能用于复杂任务需要大量计算，而衡量其有效性则需要一种细致入微的方法。这些见解为优化训练策略以增强 LLM 中的Long CoT 推理提供了实用指导。代码：https://github.com/eddycmu/demystify-long-cot。

---

1. Introduction

大型语言模型 (LLM) 在数学和编程等领域展现出卓越的推理能力。实现 LLM 推理能力的一项关键技术是思路链 (CoT) 提示，它引导模型在得出最终答案之前生成中间推理步骤。

但即使有了CoT，LLM仍然难以应对高度复杂的推理任务，例如数学竞赛、博士级科学质量保证、软件工程。近期 OpenAI 的o1模型在这些任务中取得了重大突破。这些模型的一个关键特征是它们能够利用较长的CoT来扩展推理计算，其中包括识别和纠正错误、分解困难步骤、迭代替代方法等策略，从而实现更长、更结构化的推理过程。

有多项研究尝试通过训练 LLM 生成Long CoT 来复制 o1 模型的性能，这些方法大多依赖于可验证的奖励，例如基于真实答案的准确率，这有助于避免在大规模强化学习 (RL) 中出现 reward hacking。然而，对于模型如何学习和生成Long CoT 的全面理解仍然有限。本文作者系统地研究了Long CoT 生成的潜在机制：

1. Supervised fine-tuning (SFT) for long CoTs：实现Long CoT 推理的最直接方法是SFT，分析了其扩展行为及其对强化学习的影响，发现Long CoT SFT 能够使模型达到更高的性能，并且比shot CoT 更容易的强化学习的优化；
2. Challenges in RL-driven CoT scaling：观察到强化学习并非总能稳定延长 CoT 的长度和复杂度。为了解决这个问题，作者引入了 cosine length-scaling 奖励和重复惩罚，在稳定增长 CoT 的前提下，又能鼓励诸如分支和回溯等新兴推理行为；
3. Scaling up verifiable signals for long CoT RL：可验证的奖励信号对于稳定Long CoT 强化学习至关重要。然而由于高质量、可验证数据的有限，扩大其规模仍然具有挑战性。为了解决这个问题，作者探索了使用从网络获取的包含噪声的数据。虽然这些次优监督信号会带来不确定性，但通过在SFT中适当结合并在强化学习中进行过滤，表现出了良好的前景，尤其是在out-of-domain的推理场景中，例如STEM问题解决；
4. Origins of Long CoT Abilities and RL Challenges：分支和错误验证等核心技能本身就存在于基础模型中，但有效的强化学习驱动的激励机制需要精心设计。作者研究了强化学习对long CoT 生成的影响，追踪了预训练数据中的推理模式，并讨论了衡量这些模式出现的细微差别；

---

2. Problem Formulation

本节定义符号，然后概述了用于引出 Long CoT 的 SFT 和 RL 方法。

2.1 Notation

令 $x$ 为query；$y$ 为output sequence，考虑一个以 $\theta$ 为参数的 LLM，定义了输出token 的条件分布：${\pi }_{\theta }(y_t|x,y_{1:t-1})$。

将输出中构成CoT的tokens记为 $CoT(y)\subseteq y$，CoT 通常是一个推理轨迹或解释序列。最终答案可以是一组独立的token，也可以仅仅是 $y$ 的最后一段。

使用术语长 long CoT 来描述推理标记的扩展序列，表现为比平常更长的token长度，而且还表现出更复杂的行为，例如：

1. Branching and Backtracking：模型系统地探索多条路径（branching），如果某条路径被证明是错误的，则向后回溯（backtracking）；
2. Error Validation and Correction：模型检测中间步骤中的不一致或错误，并采取纠正措施以恢复连贯性和准确性；

2.2 Supervised Fine-Tuning (SFT)

一种常见的做法是在数据集 $D_{SFT}=\{(x_i,y_i){\}}_{i=1}^N$ 上通过 SFT 初始化策略 ${\pi }_{\theta }$，其中 $y_i$ 可以是常规或long CoT 推理tokens。

2.3 Reinforcement Learning (RL)

在可选的 SFT 初始化之后，使用强化学习进一步优化长 CoT 的生成。

Reward Function

定义一个标量奖励 $r_t$ 旨在鼓励正确且可验证的推理。仅考虑基于最终答案结果的奖励，而不考虑中间步骤的基于过程的奖励，用 $r_{answer}(y)$ 来表示最终解决方案的正确性。

Policy Update

在实验中采用近端策略优化 PPO 作为默认策略优化方法。在 7.3 小节中简要讨论了强化学习方法。采用基于规则的验证器作为奖励函数，该验证器直接将预测答案与真实答案进行比较。由此产生的更新会推动策略生成能够产生更高奖励的 token。

2.4 Training Setup

采用 Llama-3.1-8B 和 Qwen2.5-7B-Math 作为基础模型，它们分别是具有代表性的通用模型和数学专用模型。对于 SFT 和 RL，默认使用 MATH 的 7,500 个训练样本提示集，并使用该提示集提供可验证的 ground truth 答案。对于 SFT，当 ground truth 答案可用时，通过拒绝抽样来合成响应。具体而言，首先对每个prompt抽取固定数量 $N$ 的候选答案，然后进行筛选，只保留最终答案与相应真实答案一致的答案。作者在类似 WebInstruct的数据上进行了实验，虽然这些数据更加多样化，但没有像 ground truth 那样的监督信号。使用 OpenRLHF 框架来训练模型。

2.5 Evaluation Setup

重点关注四个具有代表性的推理基准：MATH-500、AIME 2024、TheoremQA、MMLU-Pro-1k。鉴于训练数据主要来自数学领域，这些基准为in-domain（MATH-500 测试集）和out-of-domain（AIME 2024、TheoremQA、MMLU-Pro-1k）的评估提供了一个全面的框架。默认情况下，使用温度 $t=0.7$、$top-p=0.95$ 和最大输出长度 16,384 个tokens来生成模型。有关评估设置的更多详细信息，请参阅附录 E.1。

---

3. Impact of SFT on Long CoT

本节比较 SFT 和 RL 初始化背景下的长 CoT 数据和短 CoT 数据。

3.1 SFT Scaling

比较long CoT 与shot CoT 的第一步是为模型配备相应行为。最直接的方法是基于 CoT 数据对基础模型进行微调。由于shot CoT 很常见，因此通过从现有模型中剔除样本来整理shot CoT 的 SFT 数据相对简单。然而，如何获取高质量的long CoT 数据仍然是一个悬而未决的问题。

Setup

对于long CoT，从 QwQ-32B-Preview 中提取数据（3.3 中讨论其他long CoT 数据构建方法）；对于shot CoT，从 Qwen2.5-Math-72B-Instruct 中提取数据，这是一个在数学推理中功能强大的shot CoT 模型。具体而言，通过对每个prompt采样 $N$ 个候选答案，然后筛选出正确答案来执行拒绝抽样；对于long CoT，使用 $N\in 32,64,128,192,256$，而对于shot CoT，使用 $N\in 32,64,128,256$，为了提高效率跳过一个 $N$。在每种情况下，SFT tokens的数量都与 $N$ 成正比，基础模型为 Llama-3.1-8B。有关 SFT 设置的更多详细信息，请参阅附录 E.3。

【Note】这里初学者可能会提出疑问：如果标准答案中有一些主观描述的部分，模型输出中也有一些主观描述的内容，那么应该如何选择出正确的那条输出？通常情况下有以下四个方法：

1. 引入多维评分机制
   • 置信度评分：要求模型在给出答案的同时输出自我评估置信度，选取置信度最高的作为答案；
   • 多样性评分：剔除答案之间的语意相似性，减少高度重复的冗余答案；
   • 主观描述合理性评分：使用情感分析筛选出语意流畅的答案；
2. 使用辅助模型验证
   • 提取特征并重评分：用另外一个判别模型来对答案进行特征提取与打分；
   • 交叉验证：用多个大规模预训练模型对答案进行验证（Llama4、Qwen、GPT-4），如果一个答案在多个模型上都得到了高分，那么就用这个答案；
3. Human-in-the-loop：人工评估哪个答案最符合人类水平，但这种方式存在较高的不确定性；
4. 反向验证：根据答案让模型反向生成问题，然后再与原始问题进行对比，找到最接近的那条；

Result

Fig.1 中的虚线表明，随着 SFT tokens数量的增加，long CoT SFT 持续提升模型准确率，而短 CoT SFT 则在较低的准确率水平上提前饱和。例如，在 MATH-500 上，long CoT SFT 的准确率超过 70%，即使在 35 亿个tokens时也未达到稳定水平。相比之下，shot CoT SFT 的准确率收敛到 55% 以下，SFT tokens数量从约 2.5 亿增加到 15 亿，仅带来约 3% 的绝对提升。

3.2 SFT Initialization for RL

先前的研究表明 RL 具有比 SFT 更高的上限，作者将long CoT 和shot CoT 作为 RL 的不同 SFT 初始化方法进行比较。

Setup

使用3.1中的SFT checkpoint 初始化强化学习并训练四个周期，每个prompt采样四个响应。用PPO和MATH数据集中基于规则的验证器，并将其训练样本作为我们的强化学习提示集。使用余弦长度缩放奖励和重复惩罚，这将在章节4中详细说明。关于的强化学习设置和超参数的更多详细信息，可分别参见附录E.4和E.5.1。

Result

Fig.1 中实线和虚线之间的间隙表明，用long CoT SFT 初始化的模型通常可以通过 RL 获得更显著的提升，而用shot CoT SFT 初始化的模型则几乎无法从 RL 中获益。例如，在 MATH-500 上，RL 可以将long CoT SFT 模型的绝对精度提升 3% 以上，而shot CoT SFT 模型在 RL 前后的准确率几乎相同。

3.3 Sources of Long CoT SFT Data

为了获取long CoT 内容，作者比较了两种方法：

1. 通过提示shot CoT 模型生成原始动作并按顺序组合它们来构建long CoT 轨迹；
2. 从表现出long CoT 模式的现有模型中提取long CoT 轨迹；

Setup

为了构建较长的CoT轨迹，作者开发了一个行动提示框架 E.8，该框架定义了以下基本行为：clarify、decompose、solution step、reflection、answer。采用多步骤提示和shot CoT模型（例如Qwen2.5-72B-Instruct）来对这些行动进行排序，而更强大的模型o1-mini-0912则生成包含自我修正的反思步骤。为了提炼较长的CoT轨迹，使用QwQ-32-Preview作为教师模型。在这两种方法中，都采用MATH训练集作为提示集并使用了拒绝抽样。为了确保公平，用相同的基础模型Llama-3.1-8B，维护约20万个SFT样本，并使用与3.2中相同的强化学习设置。

Result

Table.1 显示，从涌现的long CoT 模式提炼出的模型比构造模式具有更好的泛化能力，并且可以通过 RL 进一步显著提升，而用构造模式训练的模型则不能。用涌现的long CoT 模式训练的模型在 OOD 基准 AIME 2024 和 MMLU-Pro-1k 上实现了显著更高的准确率，相对提高了 15-50%。此外，在 OOD 基准 TheoremQA 上，long CoT SFT 模型上的 RL 将其准确率显著提高了约 20%，而shot CoT 模型的性能没有变化。这也是为什么作者大部分实验都是基于提炼出的long CoT 轨迹进行的。

---

4. Impact of Reward Design on Long CoT

本节研究奖励函数设计，重点关注其对 CoT 长度和模型性能的影响。

4.1 CoT Length Stability

最近关于long CoT 的研究表明，随着思考时间的增加，模型在推理任务中的表现会自然提升。作者的实验也证实，基于从 QwQ-32B-Preview 中提炼出的long CoT 进行微调的模型，在强化学习训练中往往会延长 CoT 的长度，尽管有时并不稳定。Kimi Team 和 Hou 也指出了这种不稳定性，并已使用基于长度和重复惩罚的技术来稳定训练。

Setup

使用两个不同的模型，它们基于从 QwQ-32B-Preview 中提取的long CoT 数据进行微调，使用 MATH 训练拆分，上下文窗口大小为 16K。这两个模型分别是 Llama3.1-8B 和 Qwen2.5-Math-7B。用一个基于规则的验证器，并对正确答案设置了简单的 1 奖励，作者将其称为Classic Reward。更多详细信息请参见附录 E.5.2。

Results

两个模型在训练过程中都增加了上下文连接长度 (CoT)，最终达到了上下文窗口的极限。由于上下文连接长度超过了允许的窗口大小，这导致训练准确率下降。此外，不同的基础模型表现出不同的缩放行为。如Fig.2 所示，性能较弱的 Llama-3.1-8B 模型的上下文连接长度波动更大。

作者还发现，CoT 超出上下文窗口大小的速率在低于 1 的某个阈值时趋于平稳Fig.2。这表明超出限制开始对 CoT 长度分布施加显著的下行压力，并凸显了上下文窗口大小在隐式长度惩罚中的作用。即使没有明确的超长惩罚，轨迹也可能因为奖励或优势归一化而受到惩罚，而奖励或优势归一化在强化学习框架中都是标准做法。

4.2 Activate Scaling of CoT Length

奖励塑造可以用来稳定涌现的长度缩放。作者设计了一个奖励函数，将 CoT 长度作为额外输入，并遵循一些排序约束：

1. 正确的 CoT 比错误的 CoT 获得更高的奖励；
2. 较短的正确 CoT 比较长的正确 CoT 获得更高的奖励，这激励模型有效地使用推理计算；
3. 较短的错误 CoT 应该比较长的错误 CoT 受到更高的惩罚，这鼓励模型在不太可能得到正确答案的情况下延长其思考时间。

使用分段余弦函数易于调整且平滑，将此奖励函数称为余弦奖励Fig.3，仅在 CoT 结束时根据答案的正确性授予一次。CosFn 的公式可在附录中的Equation.1中找到。

$$R(C,L_{gen})=\{\begin{array}{ll}CosFn(L_{gen},L_{max},r_0^c,r_L^c),& \text{if }C=1,\\ CosFn(L_{gen},L_{max},r_0^w,r_L^w),& \text{if }C=0,\\ r_e,& \text{if }{L}_{gen}=L_{max}\end{array}$$

Hyperparameters:

$$\begin{array}{rl}{r}_0^c/r_0^w:& \text{Reward (correct/wrong) for }{L}_{gen}=0,\\ r_L^c/r_L^w:& \text{Reward (correct/wrong) for }{L}_{gen}=L_{max},\\ r_e:& \text{Exceed length penalty}\end{array}$$

Inputs:

$$\begin{array}{rl}C:& \text{Correctness (0 or 1)}\\ L_{gen}:& \text{Generation length}\end{array}$$

Setup

用经典奖励和余弦奖励进行了实验，使用 Llama3.1-8B 进行微调，该微调基于从 QwQ-32B-Preview 中提取的long CoT 数据，并使用 MATH 训练集拆分作为起点。更多详细信息，请参阅附录 E.5.3。

Result

余弦奖励显著稳定了强化学习下模型的长度缩放行为，从而稳定了训练准确率并提升了强化学习效率Fig.4，同时还观察到模型在下游任务上的表现有所提升Fig.5。

4.3 Cosine Reward Hyperparameters

调整余弦奖励超参数以不同方式塑造 CoT 长度。

Setup

用相同的模型进行强化学习实验，该模型基于从 QwQ-32B-Preview 中提炼出的long CoT 进行微调，但余弦奖励函数使用了不同的超参数，作者调整了正确和错误奖励 $r_0^c$ 、 $r_L^c$、$r_0^w$、$r_L^w$，并观察其对 CoT 长度的影响。更多详情，请参阅附录 E.5.4。

Result

从附录中的Fig.9 中看到，如果正确答案的奖励随着 CoT 长度的增加而增加 $r_0^c<r_L^c$，CoT 长度就会爆炸式增长；正确奖励相对于错误奖励越低，CoT 长度就越长。作者将其解读为一种训练有素的风险规避机制，其中正确奖励和错误奖励的比例决定了模型对答案的置信度，才能使其在以答案终止 CoT 时获得正的预期值。

4.4 Context Window Size

更长的上下文会给模型更大的探索空间，随着训练样本的增加，模型最终会学会利用更多的上下文窗口。这就引出了一个有趣的问题：是否需要更多的训练样本才能学会利用更大的上下文窗口？

Setup

使用相同的初始模型，并基于从 QwQ-32B-Preview 中提取的long CoT 数据进行微调，根据 MA​​TH 训练进行拆分，使用后者作为强化学习提示集。每次消融实验都使用了余弦奖励和重复惩罚，并使用不同的上下文窗口大小（4K、8K、16K）。更多详情，请参阅附录 E.5.5。

Result

上下文窗口大小为 8K 的模型表现优于 4K 的模型，这与预期一致。然而，观察到 8K 的性能优于 16K 的性能。这三个实验都使用了相同数量的训练样本Fig.6。作者认为这表明模型需要更多的训练计算才能学会充分利用更长的上下文窗口大小。

4.5 Length Reward Hacking

在获得足够的训练数据后，该模型开始出现 reward hacking 迹象，即它通过重复而不是学习解决难题来增加其在难题上的分支时间 CoT 的长度，同时模型的分支频率有所下降，这是通过计算枢纽关键词 “alternatively” 在CoT中出现的次数来估算的Fig.10。

通过使用一个简单的 N-gram 重复惩罚（Algorithm 1）来缓解这个问题。该惩罚用于重复的 token，而非对整个CoT轨迹进行评估，在计算回报时降低重复惩罚也是有效的。关于重复发生位置的具体反馈，大概能让模型更容易学会避免重复。

Setup

使用 Llama3.1-8B，该模型基于从 QwQ-32B-Preview 中提取的long CoT 数据进行了微调。两次强化学习训练，均使用了余弦奖励，但分别使用了重复惩罚和未使用重复惩罚。更多详细信息，请参阅附录 E.5.6。

Result

重复惩罚导致更好的下游任务性能和更短的 CoT，这意味着推理计算的效率更高Fig.5。

Observation

实验揭示了重复惩罚、训练准确率、余弦奖励之间的关系。当训练准确率较低时，余弦奖励会对 CoT 长度施加更大的上行压力，导致通过重复进行的奖励黑客攻击增加。这反过来又需要更强的重复惩罚。未来的工作可以进一步研究这些相互作用，并探索动态调整方法以实现更好的优化。

4.6 Optimal Discount Factors

假设使用时间局部性（即较低的折扣因子）的重复惩罚会最有效，因为其能提供关于特定违规token的更强信号。然而作者发现，当余弦奖励的折扣因子过低时，性能会下降。

为了对两种奖励类型进行最佳调整，作者修改了 PPO 中的 GAE 公式，使其能够适应多种奖励类型，每种奖励类型都有各自的折扣因子 $\gamma :{\hat{A}}_t={\sum }_{l=0}^L{\sum }_m^M{\gamma }_m^l{r}_{m,t+l}-V(s_t)$。作者在这里设定 $\lambda =1$，实验证明该方案是可行的，虽然并未对此参数进行广泛的测试。

Setup

使用相同的 Llama3.1-8B 模型，并在 QwQ-32B-Preview 提取的long CoT 数据上微调，开展了多次强化学习实验。使用余弦奖励和重复惩罚，但采用了不同的折扣因子组合。更多详情，请参阅附录 E.5.7。

Result

较低的折扣因子有效地强化了重复惩罚，而较高的折扣因子则增强了正确性奖励和超长惩罚。较高的折扣因子使得模型能够因在CoT中较早地选择正确答案而获得足够的奖励Fig.5。

观察到一个相当有趣的现象：降低余弦奖励的折扣因子会增加模型 CoT 中的分支频率，使得模型很快放弃那些似乎不能立即得出正确答案的方法 附录 D Fig.11 。作者认为这种短期思维是由于在正确答案之前获得奖励的tokens数量相对较少，这意味着通往正确答案的前的tokens被低估了，从而降低了性能Fig.5。然而，作者认为这个定性结果可能引起研究界的兴趣，因为它与延迟满足等行为与生物大脑获得的奖励分配之间的关系相似。

---

5. Scaling up Verifiable Reward

可验证的奖励信号（例如基于真实答案的奖励信号）对于稳定推理任务的long CoT 强化学习至关重要。然而，由于用于推理任务训练的高质量人工标注数据有限，因此很难扩展此类数据。为了解决这个问题，使用其他容易获取但噪声更大的数据，例如从网络语料库中提取的与推理相关的问答对。具体而言使用 WebInstruct 数据集进行实验。为了提高效率，构建了 WebInstruct-462k 一个通过最小哈希 MinHash 生成的去重子集。

5.1 SFT with Noisy Verifiable Data

研究如何将这种多样化的数据添加到 SFT 中，尽管监督数据的可靠性较低，但多样化的数据可能有助于强化学习期间模型的探索。

Setup

测试了三种配置，分别调整了不含监督数据的数据比例：0%、100%、50%，从 QwQ-32B-Preview 中提取数据进行long CoT SFT。对于含有监督信号MATH 的数据，使用真实答案进行拒绝采样；对于来自 WebInstruct 的数据，虽然没有完全可靠的监督信号，但规模更大，从教师模型中对每个提示采样一个答案且不进行过滤。对于此处的强化学习，采用与 3.2 相同的设置，使用 MATH 训练集。

Result

Table.2 显示，结合次优监督数据可提升平均性能。将 WebInstruct 数据添加到 long CoT SFT 中，与单独使用 MATH 相比，MMLU-Pro-1k 上的绝对准确率提升了 510%；混合使用 MATH 和 WebInstruct 数据可实现跨基准测试的最佳平均准确率。

5.2 Scaling up RL with Noisy Verifiable Data

比较从有噪声的可验证数据中获取奖励的两种​​主要方法：

1. 提取简短形式的答案并使用基于规则的验证器；
2. 使用能够处理自由形式响应的基于模型的验证器；

这里的一个关键因素是问答对是否可以有简短的答案。因此，比较数据集是否通过仅保留简短答案的样本进行过滤。

Setup

通过使用原始参考解决方案提示 Qwen2.5-Math-7B-Instruct 来实现基于模型的验证器。为了提取简短答案，首先提示 Llama-3.1-8B-Instruct 从原始响应中提取，然后使用 QwQ-32B-Preview 应用拒绝抽样。具体而言从 WebInstruct-462k 中为每个prompt生成两个结果，丢弃与提取的参考答案不一致的结果。此过程在 115k 个唯一提示中产生大约 189k 个响应。实验表明，拒绝抽样会丢弃许多prompt：

1. 许多 WebInstruct 提示缺乏基于规则的验证器可以有效处理的简短答案；
2. 某些提示甚至对于 QwQ-32B-Preview 来说也太难了。

对于 SFT 在过滤后的数据集上训练 Llama-3.1-8B 作为强化学习 (RL) 的初始化。强化学习阶段，未过滤设置中使用完整的 462k 个问题集，在过滤设置中使用 115k 个子集，并使用 30k 个问题集进行训练，每个问题集有 4 个答案。关于基于模型的验证器、答案提取和强化学习超参数的更多详细信息，分别请参见附录 E.5.8 & E.6 & E.7。

Result

Table.3 显示，在相同数量的 RL 样本下，带有基于规则的验证器的 RL 在经过筛选的包含简短形式答案的提示集上在大多数基准测试中均取得了最佳性能。这可能表明，经过适当筛选后的基于规则的验证器可以从嘈杂的可验证数据中生成最高质量的奖励信号。此外，与使用人工注释的验证数据 MATH 训练的模型相比，利用嘈杂但多样化的可验证数据仍可显著提升 OOD 基准测试的性能，在 TheoremQA 上的绝对增益高达 2.9%，在 MMLU-Pro-1k 上的绝对增益高达 6.8%。相比之下，将基于规则的验证器应用于未筛选的数据会导致最差的性能。这可能是因为在自由形式答案上的训练准确率较低，而基于模型的验证器性能要好得多。

---

6. Exploration on RL from the Base Model

DeepSeek-R1 已证明，通过在基础模型上扩展强化学习能力，可以实现long CoT推理。近期研究尝试通过运行相对较少次数的强化学习迭代来复制这一进展，以观察长思维链行为（例如“顿悟时刻”，这是一个突现的顿悟时刻，能够实现自我验证和修正等关键功能）的出现。本节还将探讨基于基础模型的强化学习方法。

6.1 Nuances in Analysis Based on Emergent Behaviors

自我验证行为有时会被模型的探索动作标记为突现行为或“顿悟时刻”，因为这类模式在短时间认知数据中并不常见。然而，有时自我验证行为已经存在于基础模型中，通过强化学习来强化这些行为需要满足较为严格的条件，例如强大的基础模型。

Setup

遵循 Zeng 等人的设置，使用基于规则的验证器和 PPO 算法，对大约 8000 道数学 3-5 级题目训练 Qwen2.5-Math-7B，同时也使用了作者自己基于规则的验证器实现。在推理方面，温度 $t=0$（贪婪解码），初步实验表明，对于直接通过 Qwen2.5-Math-7B 强化学习获得的模型，$t=0$ 通常表现显著优于 $t>0$。考虑到训练上下文的长度为 4096 个 token，使用的最大输出长度为 4096 个 token；对基础模型使用了零样本提示 (zero-shot prompting)，以避免在输出模式中引入偏差。从先前研究中的long CoT案例中选取了五个具有代表性的关键词：“wait”、“recheck”、“alternatively”、“retry”、“however”，并计算它们的出现频率，以量化模型自我验证的程度。关于强化学习超参数的更多细节，请参见附录 E.5.9。

Result

Fig.7 显示，基于 Qwen2.5-Math-7B 的强化学习有效地提升了准确率，但并未增加基础模型输出中存在的“重新检查”模式的频率，也未能有效地激励其他反射模式，例如“重试”和“另外”。这表明，基于基础模型的强化学习虽然显著提升了性能，但并不一定会激励反射模式。有时，基础模型的输出中也存在此类行为，而强化学习并不能显著增强这些行为。因此可能需要更加谨慎地识别突发行为。

6.2 Nuances in Analysis Based on Length Scaling

长度的增加被认为是模型有效探索的另一个重要特征。然而，有时长度的增加会伴随 KL 散度的减小，这增加了长度可能受到 KL 惩罚的影响，只是回归到基础模型的较长输出，而不是反映出长 CoT 能力的获得。

Setup

设置与 6.1相同。除了输出token长度之外，还计算了“coding rate”。由于Qwen2.5-Math-7B同时使用自然语言和编码来解决数学问题，因此如果模型输出包含“python”，则将模型输出归类为“coding”，这里的“coding”输出实际上是自然语言输出的一种特殊形式，其中的代码不会被执行，代码的输出是由模型生成的。

Result

Fig.8 (1) 显示，输出 token 的长度在初始下降之后有所增加，但从未超过基础模型的初始长度。

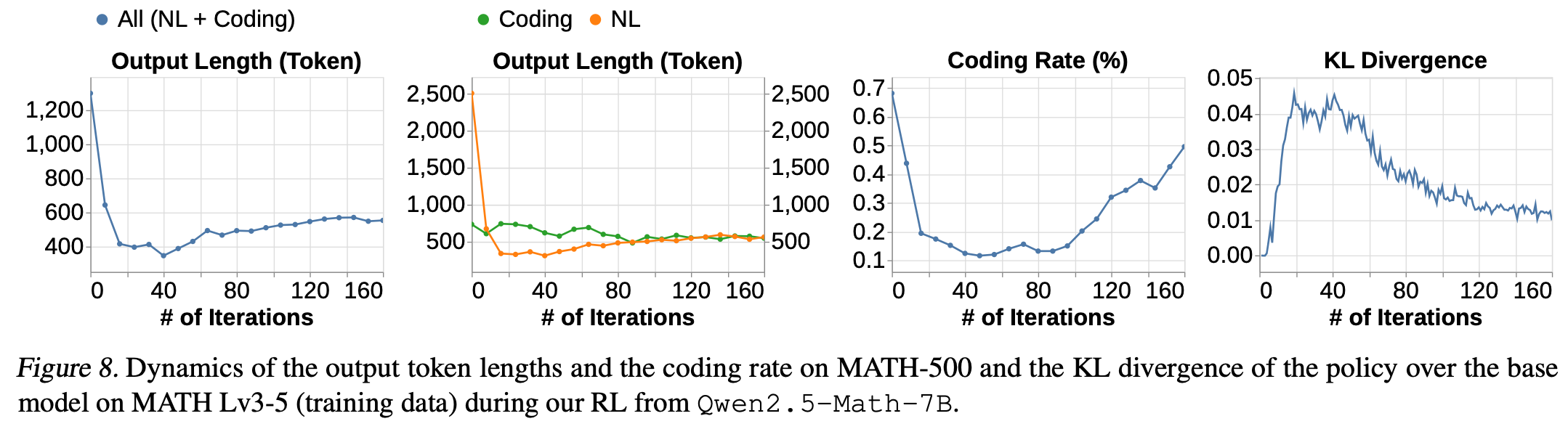
Zeng 等人认为，初始下降可能是由于模型从生成较长的编码输出过渡到生成较短的自然语言输出。然而Fig8 (2)表明，自然语言输出实际上比编码输出更长，并且初始长度的下降在两种类型的输出中均有发生。此外Fig.8 (3)显示编码率随后再次上升，这表明编码和自然语言之间的区别可能不会对优化过程产生显著影响。

作者怀疑后续的长度扩展并非源于模型的探索，因为当长度扩展时，策略相对于基础模型的 KL 散度会下降，如Fig.8 (4) 所示。这可能表明 KL 惩罚影响了长度。如果是这样，那么由于探索受到 KL 约束的限制，策略输出长度几乎不可能超过基础模型的长度。

6.3 Potential Reasons Why Emergent Behavior is NOT Observed with Qwen2.5-Math-7B

对 Qwen2.5-Math-7B 强化学习模型进行了详细分析，结果表明它未能完全复制 DeepSeek-R1 的训练行为。作者确定了以下潜在原因：

1. 基础模型相对较小（7B 参数），在受到激励时可能缺乏快速发展此类复杂能力的能力；
2. 该模型可能在（持续的）预训练和退火过程中过度暴露于类似 MATH 的短指令数据，导致过拟合并阻碍了long CoT 行为的发展。

6.4 Comparison between RL from the base Model and RL from Long CoT SFT

比较来自基础模型的 RL 和来自long CoT SFT 的 RL 的性能，发现来自long CoT SFT 的 RL 通常表现更好。

Setup

使用基础模型 Qwen2.5-Math-7B 进行比较。基础模型的强化学习结果来自6.1 中训练的模型。对于long CoT SFT 的强化学习，采用与 3.2 类似的设置。选择 7.5k MATH 训练集作为提示集，使用 QwQ-32B-Preview 对每个提示进行 32 个候选答案的拒绝采样来整理 SFT 数据，并使用带有重复惩罚的余弦长度缩放奖励和基于规则的验证器执行 PPO，每个提示采样 8 个答案并训练 8 个 epoch。为了使训练前上下文长度仅为 4096 个 token 的 Qwen2.5-Math-7B 适应long CoT SFT 和强化学习，将其 RoPE $\theta$ 乘以 10 倍。由于long CoT SFT 的经典奖励机制会崩溃，因此这里没有对比其在强化学习中的应用结果。为了进行评估，采用 2.5 中long CoT SFT 强化学习的默认温度采样设置，以及 6.1 中基础模型强化学习的贪婪解码设置，以获得最佳性能。关于蒸馏、SFT 超参数和强化学习超参数的更多详细信息，可分别参见附录 E.2、E.3 和 E.5.9。

Result

Table.4 显示，在 Qwen2.5-Math-7B 上，基于long CoT SFT 模型初始化的强化学习性能显著优于基于基础模型的强化学习，并且比long CoT SFT 本身的性能有了进一步提升。具体而言，基于余弦奖励的long CoT SFT 的强化学习平均比基于基础模型的强化学习高出 8.7%，并且比 SFT 初始化的性能提升了 2.6%。值得注意的是，仅仅将 SFT 与从 QwQ-32B-Preview 中提炼出的long CoT 结合使用就已经获得了强劲的性能。

6.5 Long CoT Patterns in Pre-training Data

根据6.1中的结果，假设一些激励行为，例如模型重新访问其解决方案，可能在预训练过程中已经部分习得。为了验证这一点，采用了两种方法来评估此类数据是否已经存在于网络上。

首先，使用生成式搜索引擎 Perplexity.ai 来识别明确包含问题解决步骤的网页，这些步骤从多个角度解决问题，或在提供答案后进行验证，使用的查询和识别的示例见附录 F.1。

其次，使用 GPT-4o 生成了一个表征“顿悟时刻”的短语列表（附录 F.2.1），然后使用 MinHash 算法搜索 OpenWebMath，这是一个从 CommonCrawl中筛选出来的数据集，该数据集在预训练中经常使用。发现在讨论主题中存在大量匹配，其中多个用户之间的对话与long CoT 相似，并且讨论了多种方法以及回溯和错误纠正（附录 F.2.2）。这提出了一个有趣的可能性，即long CoT 起源于人类对话，尽管讨论是 OpenWebMath 中常见的数据来源。

基于这些观察，作者假设强化学习主要引导模型将其在预训练期间已内化的技能重新组合成新的行为，从而提高复杂问题解决任务的表现。鉴于本文的研究范围广泛，对这部分更深入研究留待未来研究。

---

7. Discussions and Futrue Work

在本文中，揭秘了LLM中long CoT推理的过程。本节概述了未来的潜在研究方向。

7.1 Scaling up Model Size

作者认为，模型大小是限制 6.1 小节中观察到的行为出现的主要因素。Hyung Won Chung 等论文也表达了类似的观点，认为较小的模型可能难以发展高级推理能力，而更倾向于依赖基于启发式的模式识别。未来的研究可以使用更大的基础模型来探究强化学习。

7.2 RL Infrastructure Is Still in Its Infancy

在尝试扩大模型规模时，当扩展到 32B 时遇到了巨大的挑战，最终确定所需的 GPU 数量太大而无法继续。观察到开源 RL 框架（例如 OpenRLHF）通常会协调针对不同训练和推理工作负载进行优化的多个系统，这会导致内存中存储模型参数的多个副本。此外，像 PPO 这样的算法会同步且顺序地在这些工作负载之间交替，进一步限制了效率。这些因素导致了硬件利用率低，这个问题在long CoT 场景中尤其严重，因为 CoT 长度的差异较大，导致推理过程中出现落后者。作者期待机器学习和系统研究的进步将有助于克服这些限制并加速long CoT 建模的进程。

7.3 Reinforce Is More Tricky to Tune than PPO

作者还探索了 REINFORCE++ 作为 PPO 的更快替代方案用于扩展数据。然而，发现它比 PPO 明显不稳定，导致训练准确率较低Fig.13。由于这种不稳定性可能是由于未调优的设置造成的（附录 E.5.10），作者将其作为一项观察结果提出但不会对其进行评价，希望对社区有所帮助。

7.4 Scaling up Verification

研究结果表明，将基于规则的验证器与提示集过滤相结合非常有效，但设计此类规则并跨不同领域策划提示集仍然需要大量劳动力。更重要的是，这种方法将人为设计的启发式方法嵌入到强化学习环境中，反映了人类的思维习惯，而不是涌现式学习。正如《The Bitter Lesson》中所强调的那样，手动编码人类直觉往往是一种低效的长期策略，如何有效地扩展验证信号是一个值得探讨的话题。在设计强化学习环境的背景下，是否存在与预训练相当的东西，作者期待未来对次优级监督信号以及强化学习验证中自监督方法的潜力进行研究。

7.5 Latent Capabilities in Base Models

推理是基础模型中一项最近才被解锁的潜在能力。实验表明，这种思维的一个可能来源是互联网论坛上的人类对话。这引出了一个更广泛的问题：还有哪些其他能力等待从预训练数据中蕴含的海量人类知识和经验中被挖掘出来？作者期待更详细的分析，将模型行为追溯到其数据来源，从而可能产生新的见解，并有助于揭示基础模型中隐藏的能力。