当前位置：首页 > news >正文

BRAFAR: Bidirectional Refactoring, Alignment, Fault Localization, and Repair...

news 来源：原创 2025/5/23 11:07:16

BRAFAR：用于编程作业的双向重构、对齐、故障定位与修复

基本信息

作者

Xie Linna, Li Chongmin, Yu Pei, Zhang Tian, Pan Minxue（Nanjing University）

CCS 概念

社会和专业主题 → 计算机教育
计算理论 → 程序分析

关键词

程序修复、编程教育、软件重构

摘要

随着编程教育需求的增长，自动为入门级编程作业（IPAs）生成反馈的问题受到了广泛关注。尽管现有方法（如 Refactory）采用“逐块修复”策略取得了有希望的结果，但仍存在两个局限性。首先，Refactory 分别对正确和有错误的程序随机应用重构和变异操作以对齐它们的控制流结构（CFS），但成功率相对较低，且经常使原始修复任务复杂化。其次，Refactory 为有错误程序的每个基本块生成修复，当其语义与正确程序中的对应块不同时，这种方法忽略了基本块在程序中的不同作用，经常产生不必要的修复。为此，我们提出了针对 IPAs 的反馈生成方法 BRAFAR。BRAFAR 的核心创新在于其新颖的双向重构算法和粗粒度到细粒度的故障定位。前者通过以引导的方式对两个程序应用语义保持重构操作来对齐有错误程序和正确程序的 CFS，而后者则基于语句及其所包含语句的语义来识别真正需要修复的基本块。在对 1783 个真实的错误学生提交程序（来自一个公开数据集）的实验评估中，BRAFAR 显著优于 Refactory 和 Clara，以更短的时间为更多的错误程序生成了正确修复，且修复补丁更小。

1. 介绍

从计算机科学到心理学等各类大学科目的编程教育需求显著增长。众多学生参加线下编程课程和大型开放式在线课程（MOOCs），这使得教师难以及时提供个性化反馈。有效的反馈对学习至关重要，但在大规模环境中完成这项任务变得不切实际。仅仅提供失败的测试用例或教师的解决方案作为反馈往往不足。为解决这一问题，研究人员探索了自动反馈生成方法，以提供更有针对性的反馈，帮助学生有效理解和解决编码问题。

其中一条研究路线利用错误模型（手动构建或从数据中学习）来纠正学生的编程错误。然而，这些方法仍需要人工努力或修复率较低。另一条研究路线（包括 Clara、Sarfgen 和 Refactory）利用正确程序的语料库，并采用“逐块修复”策略，分别对齐错误程序和参考正确程序之间的控制流和数据流，取得了令人瞩目的修复结果。同时，这些方法也在努力生成更小的补丁。最近的技术引入了新的修复策略，但也带来了局限性，例如 AssignmentMender 依赖于自动故障定位（AFL），而 Verifx 需要匹配函数和循环结构。因此，我们的方法也采用了“逐块修复”策略。

“逐块修复”策略是一种有前景的方法，它利用代码的局部结构。它以有错误程序和具有相同控制流结构的正确参考程序作为输入，旨在通过替换有错误程序中每个基本块的表达式来生成修复，这些表达式来自参考程序中的对应块。这缩小了搜索空间并保留了有错误程序的整体结构。然而，尽管其具有潜力，但仍存在两个主要挑战：（1）如何利用正确程序来修复具有不同控制流结构的有错误程序？（2）如何最小化不必要的块修复次数，以帮助学生理解？

我们的方法如下：为了应对第一个挑战，我们引入了一种新颖的双向重构算法。该算法为两个具有不同控制流结构的程序提供双向重构指导，对齐控制流结构而不引入任何语义更改。这避免了向有错误程序引入新错误的风险。为了应对第二个挑战，我们将粗粒度到细粒度的故障定位方法与语句匹配技术集成到“逐块修复”策略中。这种组合通过减少不必要的修复并提高整体修复质量来优化修复过程。实现与评估：我们将上述方法实现为一个名为 BRAFAR 的工具，并对其性能进行了评估。通过使用 Refactory 基准测试中的 1783 个真实世界错误学生程序进行的实验表明，与最新工具 Refactory 和 Clara 相比，BRAFAR 实现了更高的修复率、更小的补丁大小和更少的过拟合。同时，我们设计了额外的实验来分别评估双向重构算法的性能以及与故障定位集成的修复策略。实验结果表明，这两个组件在减少不必要的修复和提高修复质量方面发挥了关键作用。此外，我们对 ChatGPT 的性能进行了初步评估，以强调在当前大型语言模型（LLMs）背景下我们工作的相关性和重要性。

贡献：我们的贡献总结如下：

（1）我们提出了一个用于入门级编程作业（IPAs）的通用反馈生成框架 BRAFAR。
（2）我们提出了一种双向重构算法（包括一种新颖的控制流匹配算法），以较小的修改对齐两个不同的控制流结构且不改变语义，从而有助于生成高质量的修复。
（3）我们将粗粒度到细粒度的故障定位方法与语句匹配技术集成到“逐块修复”策略中，以减少不必要的修复。
（4）我们在现实环境中对 BRAFAR 进行了评估，并公开了该工具，以便促进未来研究。

表 1：Brafar 与最相关的反馈生成方法的比较

2. 研究动机

为了更好地阐明我们方法背后的研究动机，我们对采用“逐块修复”方法的现有技术所面临的两个挑战进行了探索性研究。表 1 总结了它们的优缺点。其中，Clara 和 Sarfgen 无法为具有独特控制流或循环结构的错误程序提供反馈。它们假设总有一个正确程序具有与错误程序相同的控制流或循环结构。Refactory 通过使用重构规则生成多个正确解决方案变体来解决这一问题，但这可能导致效率和有效性方面的担忧：Refactory 只是随机重构正确代码而没有适当的指导，从而创建了巨大的搜索空间和潜在的无限代码变体，使得在有限时间内生成匹配变得困难，特别是对于复杂程序。当 Refactory 失败时，它会尝试结构变异，类似于代码差异问题，通过修改错误程序的控制流结构以匹配参考程序的结构。然而，这并未保持语义等价，通常会使原始程序的修复更加复杂，导致需要额外的、不必要的修复。

图 1：真实学生提交的动机示例

更具体地说，我们通过图 1 中的示例讨论我们方法的研究动机，该示例关注学生在顺序搜索作业中的尝试，该作业输出排序数字序列 seq 中小于 x 的数字数量。为了修复错误程序（如图 1（a）所示），Refactory 最初试图生成一个与正确程序（如图 1（b）所示）具有相同控制流结构的匹配正确变体但失败了。因此，Refactory 使用“结构变异”来修改错误程序的控制流结构以匹配参考程序的结构。这涉及删除第一个“elif”语句（第 5 行），将第二个“elif”语句（第 7 行）更新为“if”，并将“else”语句（第 9 行）更改为“elif”。这显著改变了原始错误程序的语义，导致其在更多测试套件中失败。因此，Refactory 必须投入更多精力来修复错误程序，导致需要额外的、不必要的修复，如图 1（c）所示。这个例子表明，不保持语义更改控制结构可能会导致不必要的修复和质量下降。在另一种方法中，如果我们对齐控制流结构而不引入语义更改，我们将会生成更小的补丁大小的更好修复，如实验所证明的图 1（d）所示。同时，在结构对齐后减少不必要的块修复仍然是一个挑战。尽管 Refactory 引入了规范推断和块补丁合成，但仍需要优化。我们提出将粗粒度到细粒度的故障定位方法与语句匹配集成，以生成更简洁的补丁。

3. BRAFAR 技术

我们设计并构建了 BRAFAR，这是一个用于 IPAs 的通用自动反馈生成系统——双向重构、对齐、故障定位与修复。图 2 展示了我们的方法概述。它接收三个输入：一个错误程序 $P_b$ 、（一个或多个）正确程序 C 和测试用例 T。最初，我们搜索与错误程序最近的正确程序 $P_c$ 作为修复参考。如果 $P_b$ 和 $P_c$ 具有不同的控制流结构，我们将使用一种新颖的双向重构算法（在第 3.2 节中描述）来对齐它们。然后，我们使用三个主要组件来为 $P_b$ 生成反馈：（1）对齐器（在第 3.3.1 节中描述），用于对齐 $P_b$ 和 $P_c$ 之间的块和变量。（2）故障定位器（在第 3.3.2 节中描述），用于以粗粒度到细粒度的方式定位 $P_b$ 中的可疑基本块。（3）修复器（在第 3.3.3 节中描述），接收可疑基本块及其在 $P_c$ 中的对应基本块作为输入，并输出块修复。值得注意的是，故障定位和块修复会重复进行，直到生成的程序通过所有测试套件。

3.1 搜索结果

与现有技术一样，我们的方法首先识别与错误程序最近的正确程序以进行修复。这通过考虑控制流结构的相似性然后基于整体语法细化选择来完成。首先，我们在正确程序和错误程序之间进行精确匹配，以获取它们的控制流结构（定义 3.1）。如果未找到匹配项，我们将根据控制流序列编辑距离对正确程序进行排名，并选择前 k 个（k=10）。在第二步中，我们计算错误程序与这些前 k 个程序之间的令牌级编辑距离，以识别最近的那个。

表 2：control-flowstructure节点的类型和标签

图 3：真实的学生提交

定义 3.1（控制流结构）给定程序 P，P 的控制流结构（CFS）是从抽象语法树（AST）派生的表示，它捕捉程序的控制流，同时丢弃其他细节。它通过在 AST 遍历过程中识别控制语句并为每个控制语句创建相应节点来构建。表 2 显示了三种类型的 CFS 节点。在CFS（控制流结构）构建中，一个特定的增强是添加分支节点来表示 if 语句的不同分支。图3中问题程序 $P_b$ 和正确参考程序 $P_c$ 的CFS结构在图4中展示。

这种两步法方法有效缩小了搜索空间，并充分利用了现有正确解决方案的可用性。然而，当可用的正确程序数量较少时，参考程序与被修复程序之间的相似性无法得到保证。在这种情况下，搜索过程可能变得冗余，我们工具的可行性高度依赖于双向重构算法的鲁棒性和适应性。例如，即使图3(b)中最接近的正确程序 $P_c$ 与图3(a)中待修复的问题程序 $P_b$ 具有不同的CFS结构，我们的方法仍然有效。后续章节将详细说明如何利用 $P_c$ 来修复 $P_b$ 。

3.2 双向重构

我们的双向重构目标是在不改变语义的情况下对齐错误程序 $P_b$ 和其参考程序 $P_c$ 的结构。为了保持代码的整体语义，我们的算法在过程中仔细限制重构操作，与允许添加、删除、更新或移动的结构变异不同。具体来说，我们支持以下语义保持重构操作：

类别 A. 引入新的控制流节点，规则 $R_{A_1}$ ~ $R_{A_3}$ （如图 5 所示）引入新的控制流节点而不改变语义。 $R_{A_1}$ 规则引入新的 If 语句。 $R_{A_2}$ 规则引入新的 While 语句。 $R_{A_3}$ 规则引入新的 For 语句。

类别 B. 交换条件分支，图 5 中的规则 $R_B$ 规定，在否定条件后，可以交换 If 语句不同分支中的块。

类别 C. 引入新的保护符，图 5 中的规则 $R_{C_1}$ 和 $R_{C_2}$ 在不改变语义的情况下为块 B 引入新的保护符。 $R_{C_1}$ / $R_{C_2}$ 包括两个操作：（1）添加一个条件为真/假的新 If 语句；（2）将块 B 移动到 then/else 分支。

重构规则本身很直接。我们的贡献不仅限于提供这些规则；我们还关注识别两个 CFS 之间的差异以指导重构。为此，我们提出了一种具有两个步骤的双向重构算法：（1）确定两个 CFS 之间的最佳合法匹配，（2）基于此匹配生成双向编辑脚本。

3.2.1 控制流匹配算法

双向重构的初始步骤中，我们引入了一种创新的控制流匹配算法，以建立两个 CFS 之间的最佳合法匹配。这一步骤至关重要，因为匹配的质量显著影响整个过程的成功和安全性。确保匹配的合法性至关重要，以便可以有效应用现有的重构规则（如图 5 所示），以实现结构对齐。同时，匹配长度保证了对 CFS 的最小修改。

定义 3.2（控制流序列）控制流序列是通过 CFS 的先序遍历生成的节点列表 L，其中每个节点都是树本身的元素，保留了其层次结构。L 的前 n 个节点称为 Lₙ。例如，对于 L = (M, W, If, T, E)，L₀ = ()，L₁ = (M)，L₂ = (M, W)，L₅ = (M, W₁, If, T, E)。

定义 3.3（isCompatible 函数）isCompatible(n_i, n_j) 用于判断控制流结构节点 n_i 和 n_j 是否兼容。如果满足以下条件之一，该函数返回 true：（1）两者均为方法入口；（2）两者均为分支节点；或（3）两者均为具有相同标签的控制流节点。

定义 3.4（控制流匹配）控制流匹配是两程序控制流序列之间的节点对集合。形式上，对于控制流序列 X(x₁x₂...xₘ) 和 Y(y₁y₂...yₙ)，控制流匹配 $M = \{(x_{i_1}, y_{j_1}), ..., (x_{i_s}, y_{j_s})\}$ ，其中 i₁, ..., iₛ ∈ 1..m 为不同索引，j₁, ..., jₛ ∈ 1..n 也为不同索引。∀(x, y) ∈ M 满足 isCompatible 函数的约束。若无其他匹配的长度更长，则称该匹配为“最长控制流匹配”。为找到此匹配以最小化控制流修改，可行的解决方案是最长公共子序列（LCS）算法。LCS 的工作原理如下（让函数 Longest(Q)返回 set Q 的子集，其中每个元素的长度最长）：

LCS 算法：令 $\mathrm{LCS}(X_i, Y_j)$ 表示 $X_i$ 和 $Y_j$ 之间的最长匹配集合。该问题可分解为更小、更简单的子问题，并保存解决方案以便复用。为找到 $X_i$ 和 $Y_j$ 的 LCS，我们比较 $x_i$ 和 $y_j$ 。若它们无法匹配，则 $\mathrm{LCS}(X_i, Y_j) = \mathrm{Longest} ( \mathrm{LCS}(X_i, Y_{j - 1}) \cup \mathrm{LCS}(X_{i - 1}, Y_j) )$ 。若 $x_i$ 和 $y_j$ 可以匹配，则每个匹配 $m \in \mathrm{LCS}(X_{i - 1}, Y_{j - 1})$ 通过匹配对 ( $x_i$ , $y_j$ ) 扩展，此时 $\mathrm{LCS}(X_i, Y_j) =$ $\mathrm{Longest} (\mathrm{LCS}(X_i, Y_{j - 1}) \cup \mathrm{LCS}(X_{i - 1}, Y_j) \cup (\mathrm{LCS}(X_{i - 1}, Y_{j - 1}) \oplus (x_i, y_j))$ 。例如，对于序列 X(M,W₁,W₂) 和 Y(M,W₁)，isCompatible(x₃,y₂) 返回 true，因此 LCS(X₃,Y₂)= Longest(LCS(X₃,Y₁)∪LCS(X₂,Y₂)∪(LCS(X₂,Y₁)⊕(W₂,W₁)))=
{{(M,M),(W₁,W₁)}, {(M,M),(W₂,W₁)}}。

定义 3.5（合法控制流匹配）。如果控制流匹配 M 符合现有重构规则，则认为该匹配是合法的。换句话说，合法控制流匹配识别两个 CFS 之间的重构差异，为遵守预定义规则提供基础。基于合法匹配，我们可以识别两组重构操作 $\varepsilon _{1}$ 和 $\varepsilon _{2}$ ，使得对 CFS( $P_b$ ) 应用这些操作和对 CFS ( $P_c$ ) 应用这些操作后，结果在结构上等价，即 CFS( $\varepsilon _{1}$ ( $P_b$ ))≡CFS( $\varepsilon _{2}$ ( $P_c$ ))。

考虑图 6 中的例子，两个 CFS 之间的最长公共控制流匹配 $\{(t_1.M, t_2.M), (t_1.W, t_2.W), (t_1.If, t_2.If)\}$ 被认为是非法的。这是因为 t₁ 循环外的 if 节点与 t₂ 循环内的 if 节点匹配。基于此匹配对齐两个 CFS 将需要将 t₁.If 移动到 t₁.W 的子节点。然而，图 5 中没有现有的重构规则允许这样的移动，因为这可能会改变程序的语义。为确保在每个子问题中生成匹配的合法性，额外的检查是必不可少的。因此，我们提供了四条规则来检查匹配对 ( $x_i$ , $y_j$ ) 是否可以合法地添加到给定的合法匹配 M 中，结合 CFS 的特定约束。

规则 1：如果在祖先节点集合 ancestors( $x_i$ )/ancestors( $y_j$ ) 中存在任何已匹配的 CFS 节点 $x_c$ / $y_c$ （即 ( $x_c$ , $y_c$ ) ∈ M），则与 $x_c$ / $y_c$ 在 M 中匹配的对应节点 $y_d$ / $x_d$ 也必须是 $y_j$ / $x_i$ 的祖先节点。节点 n 的祖先节点（ancestor nodes）定义为从根节点到节点 n 的路径上的所有节点。

如图 7(a) 所示，对 (t₁.If₂, t₂.If₂) 不能合法地添加到 M ({(t₁.M, t₂.M), (t₁.If₁, t₂.If₁)}) 中，因为 t₂.If₁ 和 t₂.If₂ 是兄弟节点，它们与 t₂.If₁ 和 t₂.If₂ 匹配，而 t₂.If₁ 不是 t₁.If₂ 的祖先。

规则 2：如果 $x_i$ 和 $y_j$ 是分支节点，M 应该包含对 (parent( $x_i$ ), parent( $y_j$ ))。

如图 7(b) 所示，对 (t₁.T, t₂.T₂) 不能合法地添加到 M ({(t₁.If, t₂.If)}) 中。这是因为 M 不包含对 (t₁.If, t₂.If₁)。（节点 t₁.T 应该与 t₂.T₁ 匹配，因为它们都表示匹配的 if 语句的 then 分支。）

规则 3：如果节点 $x_i$ / $y_j$ 是循环节点的后代节点（descendant），则在 $x_i$ 的祖先节点集合 ancestors( $x_i$ ) 或 $y_j$ 的祖先节点集合 ancestors( $y_j$ ) 中，所有循环节点 $x_c$ 或 $y_c$ 必须在匹配集合 M 中完成匹配。

如图 7(c) 所示，对 (t₁.If₁, t₂.If) 不能合法地添加到 M ({(t₁.M, t₂.M)}) 中。这是非法的，因为 t₂.If 是循环节点 t₂.W 的后代，而 t₁.If 不是。没有重构规则允许向 t₁.If 添加一个 while 父节点来对齐它们的控制流结构。

规则 4：如果节点 $x_i$ / $y_j$ 是未匹配的Else节点的后代节点（此场景发生于当的父节点未匹配时），则的 then 分支的所有后代节点在匹配集合 M 中必须保持未匹配状态。

如图 7(d) 所示，对 (t₁.W₂, t₂.W₂) 不能合法地添加到 M ({(t₁.M, t₂.M), (t₁.W₁, t₂.W₁)}) 中，因为 t₂.W₂ 是未匹配的 else 节点 t₂.E 的后代，但 t₂.If 的 Then 分支的后代 t₂.W₁ 在 M 中匹配。（同一分支的节点 t₁.W₁ 和 t₁.W₂ 与不同分支的 t₁.W₁ 和 t₁.W₂ 匹配。）

定义 3.6（合法扩展）给定一组合法匹配集合 Q 和一个节点对 ( $x_i$ , $y_j$ )，通过 ( $x_i$ , $y_j$ )对 Q 的合法扩展（记作 Q⊙ ( $x_i$ , $y_j$ )）定义如下：

对于 Q 中每一个可被 ( $x_i$ , $y_j$ ) 合法扩展的匹配 q，用 ( $x_i$ , $y_j$ ) 扩展该匹配 q
Q 中无法被合法扩展的匹配保持不变

然而，在 LCS 算法中引入额外的检查会损害全局解决方案的最优性。这是因为动态规划依赖于最优子结构原则，即每个子问题的解决方案必须是最佳的，并且不受其他条件的影响。因此，我们提出了一种基于 LCS 算法的新型极长合法匹配（ELLM）算法，通过将子问题转换为在控制流结构之间找到一组极长合法控制流匹配来维护最优子结构属性。

定义 3.7（极长合法匹配）两个控制流结构（CFS）之间的合法控制流匹配集合
$\mathcal{M}(\{(x_{i_1}, y_{j_1}), \dots, (x_{i_s}, y_{j_s})\})$ 仅当该匹配集不是其他任何合法控制流匹配的子集时，才被视为极其长的合法匹配（Extremely Long Legal Match）。

ELLM算法

符号定义
• ELLM ( $X_i$ , $Y_j$ )：表示节点 $X_i$ 和 $Y_j$ 之间的所有极其长的合法匹配集合。

• 最优值函数：

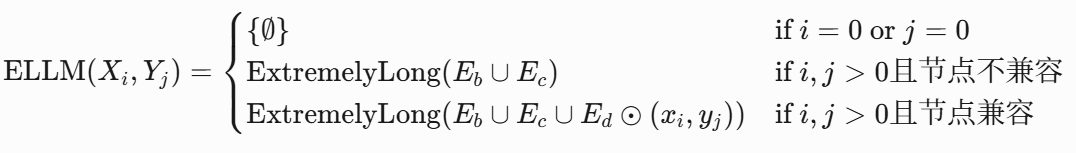
• 变量说明：

$E_b = \mathrm{ELLM}(X_{i - 1}, Y_j)$ ， $E_c = \mathrm{ELLM}(X_i, Y_{j - 1})$ ，

$E_d = \mathrm{ELLM}(X_{i - k}, Y_{j - k})$ ，其中 $\quad k = \min\{k \in [1, \min(i, j)] \mid \exists M \in \mathrm{ELLM}(X_{i - k}, Y_{j - k}), M$ 可被 ( $x_i$ , $y_j$ ) 合法扩展 $\}$

ExtremelyLong(Q)：从集合 Q 中筛选出所有不被其他匹配子集包含的匹配。
算法分支逻辑
• 分支1（终止条件）：若 i=0 或 j=0，返回空集 {∅}。

• 分支2（节点不兼容）：若节点 $x_i$ 和 $y_j$ 不兼容（如类型或结构冲突），合并 $E_b$ 和 $E_c$ 后筛选出最长匹配。

• 分支3（节点兼容）：若节点兼容，合并 $E_b$ 、 $E_c$ 和 $E_d$ 的合法扩展结果后筛选最长匹配。

定义 3.8（FindBestMatch 函数）函数 findBestMatch 选择两个序列之间的所有极长合法匹配中的最佳匹配。最佳匹配的确定分为两步：（1）根据循环节点映射的数量对匹配进行排名，并选择具有最大值的匹配，（2）考虑所选匹配中的总节点映射数量。在我们的方法中，循环节点映射优先于 If 节点映射，以确保与重复和迭代行为相关的 CFS 尽可能准确地对齐。

控制流匹配算法。该算法通过一个真实示例进行了说明。考虑到图 4 中 $P_b$ 和 $P_c$ 的 CFS，它们之间的最佳匹配显示在同一图中。生成该匹配的步骤如下：（1）首先，将两个 CFS 转换为控制流序列 X(M, W, If, T, E) 和 Y(M, W, If, T)。（2）然后，在这两个序列上运行 ELLM 算法，识别出一组极长合法匹配：{ {(M, M), (W, W)} }，以及（3）最后使用 FindBestMatch 函数来确定最佳合法匹配，结果为 {(M, M), (W, W)}。

3.2.2 总体算法

算法 1 显示了双向重构过程的总体情况（其中函数 add(a, b, i) 或 move(a, b, i) 表示引入或移动节点 a 到节点 b 的子列表的索引 i）：（1）首先，我们对两个 CFS $t_1$ 和 $t_2$ 应用控制流匹配算法以获得原始最佳合法匹配 M。特别地，如果此匹配包含一对，其中一个 CFS 中的“if”语句的“then”分支与另一个 CFS 中的“else”分支匹配（如图 8 所示），我们将使用重构规则 $R_B$ 来交换 $t_2$ 中某些“if”节点的分支。上述过程将重复进行，直到不再需要分支更改（行 1-7）。（2）接下来，我们遍历通过前序遍历生成的 CFS $t_1$ 的控制流序列 X。对于 M 中每个未匹配的节点 x，我们将使用重构规则 $R_A$ 在 CFS $t_2$ 中引入新的控制流节点 $y_n$ 并将新对 ( $x$ , $y_n$ ) 添加到 M 中（行 13-16）。特别是，如果引入了新的分支节点 $y_n$ ，我们将根据重构规则 $R_C$ 重新定位其子节点（行 17-21）。（3）同样，我们然后遍历通过前序遍历生成的 CFS $t_2$ 的控制流序列 Y，并重复上述过程以重构 CFS $t_1$ （行 8）。对图 4 中的 CFS 进行对齐的重构指导如下：（i）add(newIf, $t_2$ .M, 1)，（ii）add(newT, $t_2$ .newIf, 0)，（iii）add(newE, $t_2$ .newIf, 1)，（iv）add(newIf, $t_1$ .W, 0) 和（v）add(newT, $t_1$ .newIf, 0)。更直观地，图 9（a）和图 9（b）中展示了 $P_b$ 和 $P_c$ 的重构程序，它们是通过以下方式生成的：在 $P_b$ 中引入新的 If 条件以获得重构的错误程序 $P_{r_b}$ ，并在 $P_c$ 中引入新的 If-else 条件以获得重构的正确程序 $P_{r_c}$ 。

3.2.3 讨论

双向重构的时间成本主要由控制流匹配过程决定。对于两个长度为 n 和 m 的序列，与动态规划方法（LCS）的时间复杂度为 O(n×m) 相比，由于额外的检查，我们的 ELLM 算法在最坏情况下的时间成本呈指数增长。然而，由于现实世界中的程序（尤其是学生程序）每个方法中的 CFS 节点数量通常不多，因此在大多数情况下我们的算法是实用的。

3.3 程序修复

在本节中，我们的目标是利用参考正确程序 $P_c$ 修复错误程序 $P_b$ ，前提是它们具有相同的控制流结构。这将通过三个主要组件来实现：对齐器、故障定位器和修复器。

3.3.1 对齐器

在生成准确的修复进而生成反馈方面，将参考解决方案与错误程序对齐至关重要。此过程包括块对齐和变量对齐。

定义 3.9（程序分区）程序 P 从粗粒度到细粒度被划分为块。最初，P 的函数体被划分为复合块和基本块，每个复合块由基本块分隔。然后系统地将复合块划分为更小的单元。例如，图 9（a）中的重构错误程序 $P_{r_b}$ 被划分为 {基本块、while 块、基本块（空）、if 块、基本块}。然后，将 while 块和 if 块进一步细分为更小的单元：将 while 块划分为 {while 条件（基本块）、while 循环体}，在 while 循环体内继续进行细分。程序的基本块形成集合 $\{B_i\}_{i\in 1...n}$ 。

A.块对齐。给定错误程序 $P_b$ 和参考解决方案 $P_c$ （具有相同的 CFS），由于 CFS( $P_b$ )≡
CFS ( $P_c$ )，我们可以找到块的 1-1 映射。划分程序为块的标准根据其 CFS（定义 3.9）。具有相同 CFS 的程序共享相同的程序分区条件。

B.变量对齐。此阶段的目标是将 $P_b$ 中的变量映射到 $P_c$ 中的变量。我们应用增强型定义/使用分析（Enhanced Define/Use Analysis，EDUA）来匹配具有相似定义/使用的变量。这比传统定义/使用分析（DUA）更可靠，因为它引入了一种新的相似性计算方法。

定义 3.10（变量映射）。设 Vars(P_b)={v₁, v₂, ..., vₘ}，长度为 m，表示给定错误程序 $P_b$ 的变量集合。类似地，设 Vars( $P_c$ )={u₁, u₂, ..., uₙ}，长度为 n，为正确程序 $P_c$ 的变量集合。那么，是变量的映射，其中 i₁, ..., iₛ ∈ 1..m 是不同的索引，j₁, ..., jₙ ∈ 1..n 也是不同的索引。

定义 3.11（定义/使用权重）。设函数 $W(v_p, i)$ 表示变量 $v$ 在程序 $P$ 中第 $i$ 个基本块中的定义/使用权重。如果变量 $v$ 在第 $i$ 个基本块中被定义或使用，并且第 $i$ 个基本块是 if/while 条件或 for 迭代器，则 $W(v, i) = \alpha$ ；否则， $W(v, i) = 1$ 。（我们认为控制语句具有更高的权重，并在我们的工作中将 $\alpha$ 设置为 2。）否则，如果变量 $v$ 在第 $i$ 个基本块中未被定义或使用，则 $W(v, i) = 0$ 。

定义 3.12（定义/使用相似性）：我们计算每对变量 $<v, u>$ 的相似性，其中 $v$ 在 $P_b$ 中定义， $u$ 在 $P_c$ 中定义。设函数 $f_i(v, u)$ 表示 $v$ 和 $u$ 在第 $i$ 个基本块中定义/使用相似的程度。如果 $v$ 和 $u$ 都在第 $i$ 个基本块中被定义或使用，并且第 $i$ 个基本块是 if/while 条件或 for 迭代器，则 $f_i(v, u) = \alpha$ ；否则， $f_i(v, u) = 1$ 。否则，如果 $v$ 和 $u$ 都没有在第 $i$ 个基本块中被定义或使用，则 $f_i(v, u) = 0$ 。 $v$ 和 $u$ 之间的相似性计算如下（假设有 $n$ 个基本块）：

$Sim(v, u) = \frac{\sum_{i=1}^{n} f_i(v, u)}{max(\sum_{i=1}^{n} W(v, i), \sum_{j=1}^{n} W(u, j))}$ （1）

定义 3.13（增强型定义/使用分析，EDUA）。EDUA 存储了一组使用 EDUA 匹配的变量对。EDUA 采取保守的方法，通过多轮匹配来最小化错误匹配。在第一轮中，按顺序匹配参数变量。在第二轮中，匹配相似度 $Sim(v_b, V_c) = 1.0$ 的变量 $v_b$ 和 $v_c$ 。后续轮次匹配具有逐渐放宽的相似度阈值：≥0.9, ≥0.8, ≥0.7, ≥0.6, 或 ≥0.5。对于图 9(a) 和 9(b) 中的程序，变量映射将是：{x → x, seq → seq, i → i}。

3.3.2 故障定位器

为了减少不必要的块修复，我们引入了一种故障定位技术来识别可疑块。此方法的核心概念是推断错误程序中每个块的规范，并以粗到细的方式进行故障定位。

定义 3.14（规范）。设 B 是程序 P 中的一个块，V 是在 B 中定义或使用的变量集，D 是 V 的可能值集。程序状态 S 在执行 B 时是一个映射 $\mathbb{S}$ : V → D。块 B 的规范，记为 Spec(B)，定义为输入-输出状态对的集合 $\{\langle\mathbb{S}_{I_i}, \mathbb{S}_{O_i}\rangle\}_{i \in 1,...,r}$ 其中 i 表示 V 中的第 i 个变量 $v_i$ ， $\mathbb{S}_{O_i}$ 表示当 $\mathbb{S}_{I_i}$ 作为 B 的输入状态时 $v_i$ 的输出值。具体来说，如果 B 是一个 if/while 条件，规范 Spec(B) 将包括此表达式的输出状态。

定义 3.15（规范推断）。设 $B_c$ 是正确程序 $P_c$ 中的一个块，并且 $\{ \langle \mathbb{S}^c_{I_i}, \mathbb{S}^c_{O_i} \rangle \}_{i=1}^r$ 是 $B_c$ 的规范， $B_b$ 是错误程序 $P_b$ 中的对应块，M 是一个有效的变量映射。每个输入-输出状态对 $\langle \mathbb{S}^b_{I_i}, \mathbb{S}^b_{O_i} \rangle$ 应该满足以下条件：如果在 $P_c$ 中存在一个变量 $v_{c_i}$ 被映射到 $P_b$ 中的 $v_{b_j}$ 在 M 中，并且输入状态 $\mathbb{S}^b_{I_i}$ 等于 $\mathbb{S}^c_{I_i}$ ，则输出状态 $\mathbb{S}^b_{O_i}$ 应该与 $\mathbb{S}^c_{O_i}$ 相同。

A. 规范构建。在失败的测试套件 T 上运行重构的错误程序 $P_b$ 以收集 $P_b$ 中每个块的规范。在相同的测试套件 T 上运行重构的正确程序 $P_c$ 以收集 $P_c$ 中每个块的规范。这里，输入状态指的是在执行块之前所有变量的值，输出状态指的是执行块之后这些值。

B. 故障定位。类似于程序分区，我们采用粗到细的策略来定位可疑的基本块。这个过程通过扫描错误程序函数体中的复合块和基本块来启动。如果当前块的规范不符合预期，我们认为它是可疑的。如果定位的块不是基本块，我们继续细化搜索，直到识别出可疑的基本块。例如，对于测试用例 search(42, (-5, 1, 3, 5, 7, 10))，我们首先识别图 9(a) 中的 while 块为可疑，因为在 $P_b$ 中变量 i 的输出为 0，而预期为 6。随后，我们识别 while 条件为可疑，因为它在预期为真时输出为假。

3.3.3 修复器

我们专注于仅修复可疑的基本块，以保证最小修复。关键思想是为 $B_b$ 生成块补丁，直到 $B_b$ 在语义上等同于正确程序 $P_c$ 中对应的基本块 $B_c$ 。这个过程包括两个步骤：(1) 语句匹配和 (2) 补丁生成。

A. 语句匹配。我们通过多轮匹配 $B_b$ 和 $B_c$ 之间的语句，每一轮匹配条件逐渐放宽。在第一轮中，我们匹配在替换变量名称后变得相同的语句。在第二轮中，我们匹配在交换变量顺序后变得相同的语句。在第三轮中，我们匹配包含已匹配变量的语句。在早期轮次中匹配的语句是“更安全”的匹配，并在后续轮次中排除。最后， $B_b$ 和 $B_c$ 中未匹配的语句将与空语句匹配。

B. 补丁生成。给定语句匹配 $M(B_b, B_c)$ ，我们按如下生成块补丁：给定一对 $(S_b, S_c)$ ：
- 插入修复：如果 $S_b$ 是空，意味着 $S_c$ 未匹配到 $B_b$ 中的任何语句，将生成插入修复以插入 $S_c$ 。
- 删除修复：如果 $S_c$ 是空，意味着 $S_b$ 未匹配到 $B_c$ 中的任何语句，将生成删除修复以删除 $S_b$ 。
- 修改修复：如果 $S_b$ 和 $S_c$ 都不为空，将生成修改修复以将 $S_b$ 的 AST 转换为 $S_c$ 的 AST。

执行插入或修改操作后，我们将根据已建立的变量映射将 $S_c$ 中的变量名称替换为 $P_b$ 中的那些。如果 Vars( $S_c$ ) 中的变量 $v_c$ 未匹配到 $P_b$ 中的任何变量，我们将在相应的声明块中插入一个新的变量初始化，并添加一个新的变量映射对。注意，此过程中不会删除类型为变量声明的语句。在修复整个程序后，将移除不必要的定义。

3.3.4 整体修复过程

首先，我们在错误程序 $P_b$ 和其参考程序 $P_c$ 之间对齐块和变量。接下来，我们以粗到细的方式系统地识别 $P_b$ 中的可疑基本块。在定位到可疑基本块后，故障定位过程结束，并且识别出的块会进行修复。需要注意的是，块修复仅针对单个块，但不能保证整个程序的修复。因此，我们反复进行故障定位和块修复步骤，直到修复程序通过所有测试套件。我们为程序 $P_b$ 生成了图 9(c) 中的修复程序 $P_r$ 。

3.4 实现

BRAFAR 技术已经被开发成一个同名工具。给定一个或多个参考程序和测试用例，BRAFAR 支持修复可编译的错误 Python 程序。BRAFAR 工具的实现由五个组件组成：(1) 搜索器，(2) 双向重构算法，(3) 对齐器，(4) 故障定位算法，和 (5) 修复算法。

4. 实验评估

在本节中，我们进行了一系列实验来评估 BRAFAR 的有效性和效率。评估旨在解决以下研究问题：

RQ1 总体方法在修复错误程序方面的表现如何，包括其整体有效性、效率和修复质量？

RQ2 我们的双向重构算法在对齐控制流结构方面的表现如何？

RQ3 我们的修复策略在修复具有匹配正确参考程序的错误程序方面的表现如何？

此外，我们还对 ChatGPT进行了初步评估，以讨论在当前 LLM 上下文中工作的标志。

4.1 实验设置

基准测试设置

我们在 Refactory 的大型数据集上评估 BRAFAR。该数据集包含来自 5 个不同入门级编程作业的 2442 个正确提交和 1783 个错误学生程序，以及参考程序和教师设计的测试套件。我们仅在修复通过所有测试套件时才认为修复是正确的。表 3 提供了数据集的基本信息，更多详细信息可在 Refactory 中找到。

基线反馈生成技术

我们选择了 Refactory 和 Clara 作为基线，因为它们是相关的公开 Python 反馈生成器。尽管先前的研究在相同数据集上评估了它们，但我们在相同条件下重新执行了 Refactory 和 Clara 以进行公平比较。注意，在重现 Clara 时，我们进行了一些必要的代码修改以适应数据集。由于其他最近方法（如 AssignmentMender 和 Fapr）缺乏公开可用性，因此无法进行比较。此外，由于 Verifx 专为 C 程序设计，因此被排除在我们的比较之外。

环境

所有实验均在配备 Intel® CoreTM i7-10700 CPU、32GB RAM 并运行 Ubuntu 22.04 的台式机上进行。在实验期间，所有工具均设置为单线程模式，每个错误程序的修复设置了一分钟的超时。具体来说，Clara 需要一个离线阶段来聚类正确程序，为此我们为每个作业分配了额外的五分钟超时。

4.2 RQ1：总体性能

表 3：五种 IPA 的总体结果：修复率（RR）、平均修复时间（Time）和相对补丁大小（RPS）。“%Match” 列给出了找到具有匹配 CFS 的正确程序的错误程序的百分比。

表 3 展示了 BRAFAR、Refactory 和 Clara 之间的总体性能比较。Clara 成功为 1783 个错误程序中的 69.5% 生成了正确的修复，平均耗时 0.49 秒。Refactory 为 89.7% 的错误提交生成了正确的修复，平均每项修复耗时 3.38 秒。相比之下，BRAFAR 总共为 1756 个程序（≈98.5%）生成了正确的修复，平均耗时 0.35 秒。这表明 BRAFAR 在修复更多错误提交的同时，比 Refactory 和 Clara 需要的时间更少。

4.2.1 修复率

Clara 的低修复率主要是由于其无法修复具有独特循环结构的错误程序，约占失败原因的 67.0%（543 个失败中的 364 个）。剩余失败中，Refactory 和 BRAFAR 由于其结构对齐阶段，实现了更高的修复率。BRAFAR 仅在 27 个案例中未能生成修复。BRAFAR 失败的唯一原因是参考程序中调用了未知方法。使用这些正确解决方案修复错误程序可能将未知方法调用引入错误程序，使其无法编译。Refactory 也遇到了相同的失败原因，但其失败案例更多，这主要是由于在修复过程中缺乏有效的变量映射，以及在修复过程中近一半的失败是由于异常或超时。

4.2.2 修复大小

为了进一步评估生成的补丁，我们使用 Zhang-Shasha 树编辑距离算法计算补丁大小，并通过将补丁大小除以原始错误程序的大小来归一化补丁大小，使用相对补丁大小（RPS）指标。RPS 的计算公式为 $RPS = \mathrm{Dist}(AST_r, AST_b) / \mathrm{Size}(AST_b)$ ，这是现有技术中广泛使用的指标。为了确保公平比较，我们重新计算了 Clara 的补丁大小，以使其与 BRAFAR 和 Refactory 一致。如表 3 所示，BRAFAR 生成的修复具有比 Refactory 和 Clara 更小的平均 RPS。这表明我们的修复更小，因此更易于学生理解。图 10 展示了更详细的 RPS 比较。图 10（a）比较了 RPS 的分布，图 10（b）绘制了 BRAFAR、Refactory 和 Clara 的 RPS 核密度估计（KDE）。从图 10（a）和 10（b）中，我们观察到：（1）BRAFAR 生成的修复中有 67% 的 RPS 小于 0.3，53% 小于 0.2，31% 小于 0.1；（2）当 RPS 小于 0.3 时，BRAFAR 的 RPS 值数量或密度高于 Refactory 和 Clara；当 RPS 小于 0.25 时，BRAFAR 的 RPS 值数量或密度高于 Clara。即，BRAFAR 生成的修复中有更大比例具有较小的 RPS。

4.2.3 修复质量

为了评估 BRAFAR 生成的修复质量，并将其与 Refactory 和 Clara 生成的修复进行比较，我们随机且按比例选择了 100 个错误程序，这些程序都能被 BRAFAR 和 Refactory 修复。由于 Clara 的修复性能相对较差，我们将其排除在外。然后，我们手动检查了这些工具生成的修复。总共检查了 148 个错误方法，因为第二个作业的每个错误提交平均需要修复 3 个方法。

在 148 个方法中，BRAFAR 生成了：（a）109 个仅涉及程序员会进行的必要且自然修改的最小修复，（b）22 个涉及一些不必要修改的小修复，（c）7 个虽然正确但与学生思路有偏差或完全偏离的偏离修复，以及（d）9 个修复几乎为空方法体的免费修复。由于大多数（88.5%）生成的修复是最小和小修复，因此生成的修复质量总体较高，不会导致修复后的程序偏离学生思路，因此更容易理解。与此同时，大量存在的偏离修复表明了未来改进当前修复质量的方向。一方面，为了减少大型修复的数量，我们在生成修复时应利用有关错误方法的语义和语法信息。另一方面，为了更好地使免费修复与其他现有方法的实现保持一致，修复生成过程需要纳入跨方法的语义和语法信息。

BRAFAR 在修复质量方面优于 Refactory。在 148 个错误方法中，两种工具在 90 个案例中生成了相同的修复；在 19 个案例中，它们生成了质量相当的不同修复，即最小、小、偏离或免费修复。在一个案例中，Refactory 的修复被认为更好；在剩余的 38 个案例中，BRAFAR 的修复被认为更好。在这 38 个案例中，BRAFAR 分别生成了 32 个和 6 个最小和小修复，而 Refactory 在 19 个案例中生成了偏离修复。此外，在需要更复杂修复的错误方法中，两种工具生成的修复质量差异更为显著。在 35 个错误方法中，BRAFAR 在 16 个和 13 个案例中分别生成了最小和小修复，而 Refactory 在 26 个案例中生成了偏离修复。

相比之下，Clara 在 53 个案例中未能生成修复，其中 49 个失败是由于结构不匹配问题。对于其余修复的案例，BRAFAR 和 Clara 在 65 个案例中生成了质量相当的修复。BRAFAR 在 28 个案例中生成了更好的修复，而 Clara 仅在 2 个案例中生成了更好的修复。

总体而言，我们的手动分析表明，BRAFAR 可以为错误编程作业生成高质量的修复，并且与 Refactory 和 Clara 生成的修复相比，BRAFAR 的修复通常具有相当或更好的质量。

4.2.4 采样率

正如 Refactory 报告的那样，当采样率为 0% 时，即仅使用主解决方案作为输入正确程序，Refactory 实现了超过 90% 的修复率，而 Clara 的修复准确率不到 40%。我们在相同的条件下评估了 BRAFAR 的有效性，该工具成功修复了 1783 个案例中的 1772 个（99.4%），采样率为 0%。同时，不同的采样率对 BRAFAR 修复单个错误学生程序的平均时间影响不大。因此，我们得出结论，BRAFAR 和 Refactory 修复错误编程作业的有效性对输入的正确提交数量不敏感。相比之下，Clara 依赖于多样化的正确程序。此外，BRAFAR 在输入的正确程序减少到最小时比 Refactory 更有效。

4.3 RQ2：双向重构评估

BRAFAR 和 Refactory 较高的修复率归功于它们的结构对齐算法。如表 3 所示，只有 64.5% 的错误程序具有与正确程序匹配的 CFS。为了修复剩余的 633 个程序，BRAFAR 和 Refactory 首先进行结构对齐。然而，在 233 个程序中，两种工具分别通过找到匹配的正确方法并将其作为参考，无需进一步对齐即可修复它们。本节重点关注评估 BRAFAR 和 Refactory 对剩余 339 个错误程序的结构对齐能力（包括 387 个需要结构对齐的方法），以研究它们的有效性、效率和 CFS 编辑距离。

为了帮助这些错误程序找到具有匹配结构的正确程序，Refactory 尝试使用一组重构规则生成新的正确变体。然而，Refactory 在此过程中面临有效性和效率方面的挑战，如前一节所述。对于有效性问题，Refactory 仅帮助 339 个错误程序中的 94 个（27.7%）找到新的匹配正确程序。对于效率问题，Refactory 在线重构过程中每个方法的平均时间（排除偏差值）约为 3.0 秒。为了进一步分析性能，我们参考了图 11：（1）随着方法控制结构复杂性的增加，Refactory 仅通过重构正确程序而不进行任何指导的方法在结构对齐方面显得不足且不成功。（2）Refactory 的重构过程的平均时间呈指数增长。相比之下，在应用双向重构算法后，BRAFAR 在很短的时间内（≈0.0 秒）成功实现了所有错误程序（100%）的结构对齐。

在剩下的 245 个错误程序（包含 277 个错误方法）中，Refactory 在结构对齐阶段进行了结构变异。我们关注 BRAFAR 和 Refactory 对这些程序的 CFS 修改，并在图 12 中进行了比较：（1）图 12（a）表明，BRAFAR 的大部分 CFS 修改不超过 2 次操作，且数量下降速度比 Refactory 更快。（2）图 12（b）显示，Refactory 的 CFS 修改随着 CFS 节点的增加而趋于变大。相反，BRAFAR 展现出更一致的行为。我们得出结论，在大多数情况下，我们的双向重构算法能够以较小的 CFS 修改大小实现有效的结构对齐。

此外，如第 2 节所述，Refactory 的结构变异不能保持程序的语义，最终可能需要更多精力来修复错误程序。我们简单比较了两种工具进行结构变异后错误程序通过的测试用例数量，发现 Refactory 生成的变异程序中有 63.7%（156/245）失败的测试用例更多。关注这些经历结构变异的错误程序的修复结果，Refactory 成功修复了 93.9%（230/245）的程序，平均 RPS 达到 0.68。相比之下，BRAFAR 实现了更高的修复率 99.2%，并为这些错误程序生成了平均 RPS 更小的修复（0.49）。较小的 RPS 结果是通过我们的双向重构算法和我们的集成修复策略实现的。为了单独评估双向重构算法如何帮助减少 RPS，我们创建了 Refactory+，用此算法的结果替换了结构变异的结果。混合工具对这些错误程序的平均 RPS 为 0.55。这表明 BRAFAR 能够在保持语义一致性的同时实现结构对齐，从而有助于生成更小的修复。

4.4 RQ3：修复策略评估

BRAFAR 较小的平均相对补丁大小（RPS）主要归因于其集成的修复策略，该策略结合了粗粒度到细粒度的故障定位方法。为了比较我们的修复策略与 Refactory 的策略，我们关注这些错误程序（共 1150 个），它们具有与正确提交匹配的相同 CFS，因此无需结构对齐过程。总结来说，Refactory 生成了 1119 个修复，平均 RPS 为 0.26，而 BRAFAR 生成了 1150 个修复，平均 RPS 更小，为 0.22。具体来说，对于第 1 个作业，BRAFAR 的平均 RPS 为 0.25，Refactory 为 0.31。对于第 2 个作业，BRAFAR 的平均 RPS 为 0.15，Refactory 为 0.20。对于第 3 个作业，BRAFAR 的平均 RPS 为 0.25，Refactory 为 0.27。对于第 4 个作业，BRAFAR 的平均 RPS 为 0.16，Refactory 为 0.20。对于第 5 个作业，BRAFAR 的平均 RPS 为 0.16，Refactory 为 0.18。这表明我们的集成修复策略可以帮助生成比 Refactory 更小的修复。

4.5 ChatGPT 评估

大语言模型（LLMs）的最新进展使其在编程任务中得到广泛应用。为了了解 BRAFAR 与 LLMs 在修复 IPAs 方面的比较，我们对 ChatGPT 4.0 进行了初步实验，修复了来自同一数据集的错误 Python 程序。在实验中，我们将 ChatGPT 4.0 的所有超参数设置为默认值，例如温度、max_length 和 top_p。

为了标准化流程，类型 I 的查询形式为“修复以下错误代码 $P_b$ ，尽量减少修改”，其中 $P_b$ 是错误的学生代码；类型 II 的查询形式为“修复以下错误代码 $P_b$ ，尽量减少修改，并附上测试用例 T”，其中 T 是一组测试用例；类型 III 的查询形式为“修复以下错误代码 $P_b$ ，尽量减少修改，并附上参考正确代码 $P_c$ ”，其中 $P_c$ 是教师提供的参考程序。表 4 显示了 ChatGPT 对五个 IPAs 的修复结果以及 Brafar 的结果以供参考。

我们承认，与相关工作中的实验相比，我们对 ChatGPT 的实验较为初步，不足以进行定量分析，例如我们仅使用了 ChatGPT 的默认超参数值，且未真正与 ChatGPT 交互以使其有机会完善其答案。然而，根据结果，我们对 ChatGPT 在修复 IPAs 方面的有效性做出以下两个观察：（1）首先，当未提供任何附加信息时，ChatGPT 在修复编程作业方面面临挑战，但在提供测试用例和参考实现时修复率显著提高。这表明，提供更全面的输入可能会实现更高的修复率。（2）其次，正确地将附加信息或要求编码到提示中对于 ChatGPT 有效理解和利用它们至关重要。手动检查发现，在类型 III 查询的成功修复案例中，47.2%（737/1562）中，ChatGPT 仅返回了参考程序作为修复结果。这些结果被认为价值较低，表明 ChatGPT 在理解和利用上下文信息方面的能力有限。同时，尽管指示 ChatGPT 生成“尽量减少修改”的修复，但其生成的修复比 Brafar 返回的修复大得多，表明 ChatGPT 在没有额外帮助的情况下理解和满足要求的能力也有限。

我们相信，尽管 LLMs 发展迅速并在编程任务中取得了成功，但我们的工作仍然具有意义。原因是，给定错误的学生程序、一组测试和一组非空的正确实现作为参考作为输入，存在逐步推导出高质量修复的解决方案，而 Brafar 就是这样一个系统且有效的解决方案。相比之下，尽管 LLMs 非常强大，但它们本质上是概率性的，还有很长的路要走才能完全理解和利用输入数据并持续生成高质量的修复。

4.6 实验有效性威胁

在本节中，我们将列出一些可能威胁实验发现有效性的因素。

构建有效性：我们发现的构建有效性威胁涉及实验评估中的测量是否准确捕捉了研究现象。我们将修复分类为正确，如果它通过了所有输入测试。尽管这种方法可能错误地接受错误修复（如果输入测试遗漏了程序规范的某些方面），但在编程作业评分的背景下这是合理的，因为它模仿了教师在实践中确定程序正确性的方式，并且与该领域其他研究人员评估正确性的方式一致。

内部有效性：内部有效性威胁涉及实验是否控制了可能的混杂因素。一个明显的威胁来自我们实现 Brafar 的可能错误。为了缓解这一威胁，我们在最终实验之前审查了 Brafar 的实现和实验脚本，以确保其正确性。

外部有效性：外部有效性威胁涉及实验发现是否推广到其他环境。我们在相关工作的一个数据集上评估了 Brafar，该数据集包含大量针对五个不同入门级编程作业的正确和错误实现，构成了实际入门级编程作业的良好代表。

5. 相关工作

自动反馈生成问题在过去几年中引起了广泛关注。它似乎与自动程序修复（APR）相关。然而，与专业软件相比，学生程序具有不同的特征，导致传统 APR 工具性能不佳。

我们的工作建立在先前的反馈生成技术之上，这些技术采用“逐块修复”策略。其中，Clara 通过对正确提交进行动态分析聚类，并使用它们修复具有匹配循环结构的错误程序。Sarfgen 提出了一种新方法，将 AST 嵌入数值向量以加速搜索最近的正确解决方案。它们无法为具有独特控制流/循环结构的错误程序生成补丁。Refactory 尝试通过使用重构规则创建多个正确变体来解决这一问题，但正如前面提到的，其有效性有限。

针对 OCaml 编写的学生程序的最新修复技术包括 FixML 和新发布的 Cafe。虽然 FixML 仅限于修复多位置错误，但 Cafe 利用上下文感知匹配算法通过使用多个部分匹配的参考程序分别修复方法来修复错误程序。然而，在我们的方法中，上下文敏感的 Interprocedural 分析不在讨论范围内。

新发布的自动反馈生成技术采用了不同的修复策略，但也引入了新的限制。例如，AssignmentMender 使用部分修复通过重用提交中的细粒度代码片段生成简洁的反馈。然而，其性能严重依赖于现有的自动故障定位（AFL）技术，并且在生成复杂修复（如修复多个语句）方面受到限制。另一方面，Verifx 旨在生成可验证正确的程序修复作为学生反馈。但 Verifx 无法为具有独特循环结构的错误程序生成修复。

虽然上述技术和我们的方法集中在代码级反馈，但 Fan 等人开辟了一条新途径。他们将程序抽象为“概念图”以提供概念级反馈。这些概念图包含翻译成自然语言的表达式，以增强可读性，使其更适合作为学生的提示。

像 Copilot 和 ChatGPT 这样的大型语言模型（LLMs）已被证明在代码相关任务中有效。本文对 ChatGPT 在我们的数据集上进行了评估。尽管在某些情况下表现良好，但仔细评估和验证其建议至关重要，特别是对于复杂场景。有效的提示工程，即增强 ChatGPT 性能，依赖于传统的程序分析，这突显了我们工作的持续相关性。

6. 结论

我们提出了 BRAFAR，一个用于编程作业的通用反馈生成框架。为了解决两个挑战，BRAFAR 集成了用于控制流修复的双向重构算法，并采用粗粒度到细粒度的故障定位方法以减少不必要的修复。我们在真实学生提交程序上的评估结果表明，与现有方法相比，BRAFAR 能够在更短的时间内以更小的修复大小实现更高的修复成功率。

数据可用性：在当前研究中实现/分析的工具/数据集可在 https://github.com/LinnaX7/brafar-python 找到。

启发

双方调整比单方面改更有效：改代码时，同时调整正确和错误的程序结构，让它们“对齐”，而不是只改错误代码。这样能避免把错误代码改得更乱。

保持代码功能不变的调整技巧：调整代码结构时，用一些“安全操作”，比如交换if-else分支（同时反转条件），保证程序功能不变。

小模型可以和AI大模型互补使用：ChatGPT直接改代码容易改过头，而传统方法能生成更精准的小改动。结合两者优势——用传统方法确定哪里要改，改多少，用AI生成具体修改建议。

是否可以尝试不同类型的错误使用不同的模型或方法来进行修改？

BibTex

@inproceedings{10.1145/3650212.3680326,
author = {Xie, Linna and Li, Chongmin and Pei, Yu and Zhang, Tian and Pan, Minxue},
title = {BRAFAR: Bidirectional Refactoring, Alignment, Fault Localization, and Repair for Programming Assignments},
year = {2024},
isbn = {9798400706127},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
url = {https://doi.org/10.1145/3650212.3680326},
doi = {10.1145/3650212.3680326},
booktitle = {Proceedings of the 33rd ACM SIGSOFT International Symposium on Software Testing and Analysis},
pages = {856–868},
numpages = {13},
keywords = {Program Repair, Programming Education, Software Refactoring},
location = {Vienna, Austria},
series = {ISSTA 2024}
}