求组合数【递推+快速幂+卢卡斯+线性筛】

递推 杨辉三角

可以将$C_n^m$理解为从n个不同的数中选m个有几种选法。
方案数就是$C_n^m$。
由于n，m的范围不大，可以利用递归
递归式：$C_n^m$=$C_{n-1}^m$+$C_{n-1}^{m-1}$
理解：
对第一个数有选和不选两种方式

• 不选，从剩下的n-1个数中选m个 即$C_{n-1}^m$
• 选，从剩下的n-1个数中选m-1个 即$C_{n-1}^{m-1}$

特别的，选0次时应赋值为1，以便后面递推；
时间复杂度O(n*n)

void getC()
{for(int i=0;i<N;i++){for(int j=0;j<i;j++){if(j==0)c[i][j]=1;elsec[i][j]=c[i-1][j]+c[i-1][j-1];}}
}

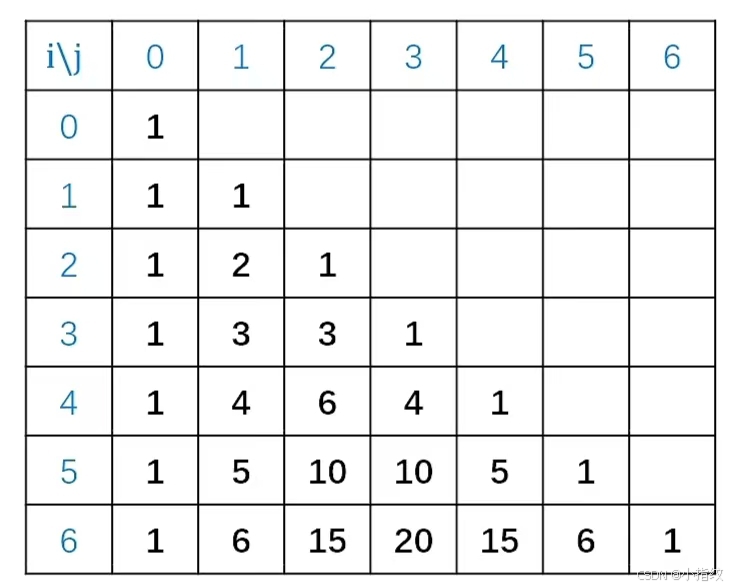
通过列表发现，与杨辉三角的规律一致。

快速幂+逆元

当n,m的范围较大时，我们就不能用递归了，因为会TLE.
考虑用阶乘公式来计算：

阶乘的逆元怎么算？

为了能清楚的理解，还是建议大家自己推导推导~

时间复杂度O(nlogP)

void qmi(int a,int b)//快速幂
{int ans=1;while(b){if(b&1)ans=ans*a%P;a=a*a%P;b>>=1; }return ans;
}
void init()//打表 
{f[0]=g[0]=1;for(int i=1;i<N;i++){f[i]=f[i-1]*i%P;g[i]=g[i-1]*qmi(i,P-2)%P;} 
}
int getC()
{return f[n]*g[m]%P*g[n-m]%P;
}

卢卡斯定理

这个n和m的范围太大了，上面两个方法都不行，就要学习新的方法啦。
这个新的方法是让m/p和n/p的组合数与m%p和n%p的组合数相乘
。

时间复杂度O(plogp+logpn)
代码很简单，会用到上面的内容

void qmi(int a,int b)
{int ans=1;while(b){if(b&1)ans=ans*a%P;a=a*a%P;b>>=1; }return ans;
}
void init()//打表 
{f[0]=g[0]=1;for(int i=1;i<N;i++){f[i]=f[i-1]*i%P;g[i]=g[i-1]*qmi(i,P-2)%P;} 
}
int getC()
{return f[n]*g[m]*g[n-m]%p;
}
int lucas(int n,int m,int p)
{if(m==0)return 1;return lucas(n/p,m/p,p)*getC(n%p,m%p,p)%p;
}

高精度 线性筛

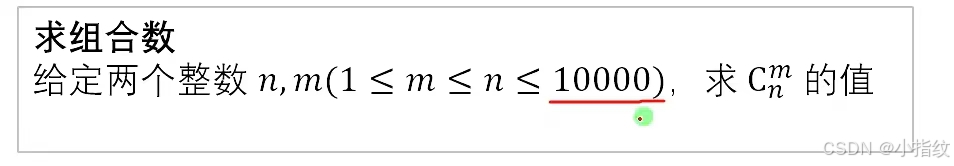
组合数的增长速度相当的快，必须用高精度来存。

• 1.筛质数，把1~n之间的质数筛出来。
• 2.枚举所有质数。
  
  代码实现：

int get(int n,int p)//n的阶乘中p的个数 
{int s=0;while(n)s+=n/p,n/=p;return s;
}
int getC(int n,int m,int p)//C中P的个数 
{return get(n,p)-get(m,p)-get(n-m,p);
}
void mul(int c[],int p,int &len)//高精度 
{int t;for(int i=0;i<len;i++){t+=c[i]*p;c[i]=t%10;t/=10;} while(t){c[len++]=t%10;t/=10;}
}
int main()
{int c[N],len=1,c[0]=1;for(int i=0;i<cnt;i++){int p=prim[i];int s=getC(n,m,p);while(s--)mul(c,p,len);}
}

题目练习

题目来源：B3717 组合数问题

题目描述

给出 $T$ 次询问，每次给出 $n,m$，请求出 $\left(\genfrac{}{}{0ex}{}{n}{m}\right)$ 对 $998,244,353$ 取模的结果。

其中 $\left(\genfrac{}{}{0ex}{}{n}{m}\right)$ 为二项式系数，它的另一种写法是 $C_n^m$。

输入格式

输入的第一行是两个整数，分别表示询问的次数 $T$ 和所给出 $n$ 的最大值 $N$。
接下来 $T$ 行，每行两个整数，依次表示给出的 $n$ 和 $m$。

输出格式

为了避免输出过大，请你输出一行一个整数，表示所有询问的结果的按位异或和。

输入 #1

3 5
3 3
4 2
5 3

输出 #1

13

说明/提示

样例 1 解释

三组询问的答案依次是 $1,6,10$。

数据规模与约定

对 $100\%$ 的数据，保证 $1\le T\le 5\times 10^6$，$0\le m\le n\le N\le 5\times 10^6$。

提示

请注意大量的数据读入对程序效率造成的影响，选择合适的读入方式，避免超时。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e6+5;
int g[N], f[N], q[N];
const int p = 998244353;
void init(int n, int p) {g[1] = 1, f[0] = 1, q[0] = 1;for(int i = 2; i <= n; i++) g[i] =  (p - p / i) * g[p % i] % p; // 线性求逆元for(int i = 1; i <= n; i++) f[i] =  f[i - 1] * g[i] % p, q[i] =  q[i - 1] * i % p; // 线性求阶乘逆元
}
signed main() {ios::sync_with_stdio(0);int ans = 0, t, maxn;cin >> t >> maxn;init(maxn, p);while(t--) {int n, m; cin >> n >> m;int a =  q[n] * f[m] % p * f[n - m] % p;ans ^= a;}cout << ans << endl;return 0;
}

如有不足，后续补充~