计算方法实验六 数值积分
【实验性质】综合性实验。
【实验目的】理解插值型积分法;掌握复化积分法算法。
【实验内容】
1对 ,用复化梯形积分和变步长梯形积分求值(截断误差不超过
,用复化梯形积分和变步长梯形积分求值(截断误差不超过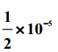 )。
)。
【理论基础】
积分在工程中有重要的应用,数值积分的基本思想是用被积函![]() 在区间
在区间![]() 上的一些点
上的一些点![]() 处的值
处的值![]() 的线性组合作为积分的近似值:
的线性组合作为积分的近似值:

实际应用中 f x( )是未知的,一般用 f x( ) 的次数不超过n的插值多项式![]() 来代替(插值型求积方法):
来代替(插值型求积方法):







【实验过程】
1.用复化梯形积分求解,给出代码,并用表格记载求解过程〔区间数n=30、50、70、100、150〕。
程序代码:
头文件:
#ifndef DEFINITEINTEGRAL_H
#define DEFINITEINTEGRAL_H
#include<math.h>
class definiteintegral
{
public:
definiteintegral();
double T_Integral(double a ,double b,double(*f)(double));
double S_Integral(double a ,double b,double(*f)(double));
double C_Integral(double a ,double b,double(*f)(double));
double Tn_Integral(double a ,double b,double(*f)(double),int n);
double Sn_Integral(double a ,double b,double(*f)(double),int n);
double Cn_Integral(double a ,double b,double(*f)(double),int n);
double V_T_Integral(double a, double b, double(*f)(double),double e);
};
#endif // DEFINITEINTEGRAL_H
主函数:
//实验六
#include <iostream>
#include <windows.h>
#include "colvector.h"
#include "matrix.h"
#include <windows.h>
#include "linearequations.h"
#include "interpolationpolynomial.h"
#include "definiteintegral.h"
double f1(double x){
return x*x*x-sin(x)-4*x-1;
}
double f2(double x){
return 3*x*x-cos(x)-4;
}
double f3(double x){
double result =sin(x)+4*x-1;
if(result>0){
return pow(result,1.0/3);
}else{
return -pow(fabs(result),1.0/3);
}
}
using namespace std;
double f4(double x)
{
return 1/(1+x*x);
}
int main()
{
SetConsoleOutputCP(CP_UTF8);
double a=0,b=1.0;
definiteintegral obj;
cout<<"梯形积分:\t\t"<<obj.T_Integral(a,b,f4)<<endl;
cout<<"Simpson积分:\t\t"<<obj.S_Integral(a,b,f4)<<endl;
cout<<"Cotess积分:\t\t"<<obj.C_Integral(a,b,f4)<<endl;
cout<<endl;
cout<<"复化梯形积分:\t\t"<<obj.Tn_Integral(a,b,f4,150)<<endl;
cout<<"复化Simpson积分:\t"<<obj.Sn_Integral(a,b,f4,30)<<endl;
cout<<"复化Cotes积分:\t\t"<<obj.Cn_Integral(a,b,f4,30)<<endl;
cout<<endl;
cout<<"交步长梯形积分:\t\t"<<obj.V_T_Integral(a,b,f4,0.00001)<<endl;
return 0;
}
代码块:
#include "definiteintegral.h"
definiteintegral::definiteintegral(){}
double definiteintegral::T_Integral(double a,double b,double(*f)(double)){
return (b-a)/2.0*(f(a)+f(b));
}
double definiteintegral::S_Integral(double a,double b,double(*f)(double)){
return (b-a)/6.0*(f(a)+4*f((a+b)/2)+f(b));
}
double definiteintegral::C_Integral(double a,double b,double(*f)(double)){
double h=(b-a)/4.0;
return (b-a)/90*(7*f(a)+32*f(a+h)+12*f(a+2*h)+32*f(a+3*h)+7*f(b));
}
double definiteintegral::Tn_Integral(double a,double b,double(*f)(double),int n){
double h=(b-a)/n;
double result =0;
double sum=0;
for(int i=1;i<=n-1;i++){
sum +=f(a+i*h);
}
result =h/2.0*(f(a)+2*sum+f(b));
return result;
}
double definiteintegral::Sn_Integral(double a,double b,double(*f)(double),int n){
double h=(b-a)/n;
double result =0;
double sum1=0,sum2=0;
for(int i=1;i<=n;i++){
sum1 +=f(a+(i-1)*h+h/2);
}
for(int i=1;i<=n-1;i++){
sum2 +=f(a+i*h);
}
result =h/6.0*(f(a)+4*sum1+2*sum2+f(b));
return result;
}
double definiteintegral::Cn_Integral(double a,double b,double(*f)(double),int n){
double h=(b-a)/n;
double result =0;
double sum1=0,sum2=0,sum3=0,sum4=0;
for(int i=1;i<=n;i++){
sum1 +=f(a+(i-1)*h+h/4);
}
for(int i=1;i<=n;i++){
sum2 +=f(a+(i-1)*h+h/2);
}
for(int i=1;i<=n;i++){
sum3 +=f(a+(i-1)*h+3*h/4);
}
for(int i=1;i<=n-1;i++){
sum4 +=f(a+i*h);
}
result =h/90.0*(7*f(a)+32*sum1+12*sum2+32*sum3+14*sum4+7*f(b));
return result;
}
double definiteintegral::V_T_Integral(double a, double b, double(*f)(double),double e){
double h=(b-a);
double T1=h/2.0*(f(a)+f(b));
double T2=T1/2.0+h/2.0*f(a+h/2.0);
double error=fabs(T2-T1);
while(error>=e){
T1=T2;
h=h/2;
double x=a+h/2;
double sum=0;
while(x<b){
sum+=f(x);
x+=h;
}
T2=T1/2.0+h/2.0*sum;
error=fabs(T2-T1);
}
return T2;
}
表格:
n=30 | n=50 | n=70 | n=100 | n=150 |
0.785352 | 0.785381 | 0.785390 | 0.785394 | 0.785396 |
2.用变步长梯形积分求解,给出代码,并用表格记载求解过程。
代码块:
double definiteintegral::V_T_Integral(double a, double b, double(*f)(double),double e){
double h=(b-a);
double T1=h/2.0*(f(a)+f(b));
double T2=T1/2.0+h/2.0*f(a+h/2.0);
double error=fabs(T2-T1);
while(error>=e){
T1=T2;
h=h/2;
double x=a+h/2;
double sum=0;
while(x<b){
sum+=f(x);
x+=h;
}
T2=T1/2.0+h/2.0*sum;
error=fabs(T2-T1);
}
return T2;
}
表格:

3.比较复化积分与变步长积分,分析实验出现的问题,总结解决办法。
复化积分是将一个区间分成若干子区间,然后在每个子区间上应用数值积分方法。它的优点是简单易实现,计算结果比较稳定。但是,如果子区间的数量不够多,或者函数在某些子区间上变化较大,可能会导致计算结果的误差较大。为了解决这个问题,可以增加子区间的数量,或者使用自适应方法,根据函数的变化情况来调整子区间的数量。
变步长积分是根据函数的变化情况,调整积分步长来提高计算精度。它的优点是能够更好地适应函数的变化情况,减小误差。但是,如果调整步长的策略不合理,可能会导致计算时间过长。为了解决这个问题,可以采用适当的步长调整策略,如自适应选取步长或者根据函数的一阶或二阶导数来调整步长。
【实验心得】
在本次实验中,我们学习了三种数值积分的方法,包括差值积分法、复化积分法和复化梯形公式。通过这些实验,我对数值积分的原理和计算方法有了更深入的了解。
在差值积分法中,我们使用了牛顿-科特斯公式对函数进行了差值,然后通过对差值多项式进行求和来计算积分。这种方法的优点是计算简单,适用于低次多项式的积分,但对于高次多项式的积分误差较大。
复化积分法是将计算区间分成若干小区间,然后对每个小区间应用数值积分方法。我们采用了复化梯形公式,其原理是通过将每个小区间近似为梯形来计算积分。这种方法误差较差值积分法要小,但计算较复杂。
综合考虑精度和计算复杂度,我们可以选择合适的数值积分方法。如果函数是低次多项式,可以使用差值积分法进行计算。对于复杂函数,可以采用复化积分法进行分区间计算。通过这些实验,我掌握了数值积分的基本原理和计算方法,并且了解了不同方法的优缺点,这对于解决实际问题具有重要的参考价值。
得 分_____________
评阅日期_____________
教师签名_____________
