大连理工大学选修课——图形学：第三四章 基本图形生成算法

第三四章 基本图形生成算法

图形生成

概念：如何在指定的输出设备上，根据坐标描述，构造基本二维几何图形

基本二维几何图形：点、直线、圆、多边形域、字符串及相关属性等。

图形生成的概念

是在指定的输出设备上，根据坐标描述构造二维几何图形。

图形的扫描转换：在光栅显示器等数字设备上，确定一个醉驾逼近于图形的像素集的过程。

光栅化

光栅就是德语中屏幕的意思，光栅化就是把图形画在屏幕上的过程，即将几何图形转化为像素化图像的过程。

基本过程：

1. 确定最佳逼近图形的像素集合。
2. 用图形的颜色或其它属性，按照扫描顺序，对像素进行某种写操作，完成图形在屏幕上的显示。

直线段和圆的光栅化

直线段和圆是最基本的图形元素，包括以下几种算法：

直线光栅化算法：DDA算法、Bresenham算法

圆光栅化算法：Bresenham画圆算法、中点算法、中点整数算法、中点整数优化算法。

直线的光栅化算法

要求：直、精确的起始点、亮度颜色均匀且沿直线不变，与直线长度、方向无关、快。

DDA算法

David F.Rogers的描述（适用于所有象限）

步骤如下：

1. 如果已知第$i$点的坐标，利用步长$StepX$和$StepY$，得到第$i+1$点的坐标，$i+1$点的坐标为：

$$x_{i+1}=x_i+StepX{y}_{i+1}=y_i+K\cdot StepX$$

1. 如图所示，$K<1,StepX=1，StepY=k$，将直线上每个点的坐标四舍五入，得到光栅点的位置：

   

James D.Foley的描述（只适用于第一象限，且K<1）

令：

$$k=\frac{y_2-y_1}{x_2-x_1}$$

有：

$$y_{i+1}=y_i+k\cdot StepX$$

若$0<k<1$，则$△x>△y$。

因为光栅单位为1，每次$x$方向增加1，y方向增加k，得到下一个直线点。

现有算法描述分析

Rogers：

采用$x_{i+1}=x_i+StepX{y}_{i+1}=y_i+K\cdot StepX$，逼近点并不是直线最好的逼近

D.Foley：可能引起累积误差

未分析直线端点不在像素点的情况，且只给出$0°$-$45°$的第一卦限的情况。

每次步长为一个单位，减少累积误差。

本教程描述——任意方向插补算法

if (fabs(dy)<fabs(dx)) {     //X方向长 ， 斜率 <=1Length=abs(Round(xe)-Round(xs));Flag=1; //最大的插补长度和方向标记ix= Round(xs); //初始 X点idx=isign(dx); //X方向单位增量y= ys+dy/dx*((float)(ix)-xs); //初始 Y点修正dy=dy/fabs(dx); //Y方向斜率增量
}else { // Y方向长 ， 斜率 >1Length=abs(Round(ye)-Round(ys));Flag=0;iy= Round(ys); //初始 Y点idy=isign(dy); //Y方向单位增量x= xs+dx/dy*((float)(iy)-ys); //初始 X点修正dx=dx/fabs(dy); //X方向斜率增量
}

Bresenham算法

Bresenham算法：

从另一个角度看直线光栅化显示算法的原理：由直线的斜率确定选择在$x$方向或$y$方向上每次递增1个单位，另一变量递增量为0或1，取决于实际直线与网格点的距离，四舍五入。

1. 基本原理

   假定直线斜率k在$0$-$1$之间，此时，$x$方向每次递增一个单位，决定$y$方向每次递增0或1。

   (斜率大于1，y每次递增1，小于1，x每次递增1）

   假设：当前点为$(x_i,y)$，当前光栅点为$(x_i,y_i)$

   则下一点为： ( x i + 1 , y + k ) , k ∈ { 0 , 1 } (x_i+1,y+k),k\in\{0,1\} (xi​+1,y+k),k∈{0,1}

   

   记直线与它垂直方向最近的下光栅点误差为$d$。

   当$d<0.5$：下一像素点为$(x_i+1,y_i)$

   当$d>0.5$：下一像素点为$(x_i+1,y_i+1)$

1. 对bresenham的简化

   令$e=d-0.5$，关于d的判别式和初值可简化成：

   $e<0$：取$(x_i+1,y_i)$

   $e>0$：取$(x_i+1,y_i+1)$，$e=e-1$

2. 整数Bresenham算法

   上述Bresenham算法在计算直线斜率和误差项时需要浮点运算和除法，采用整数算术运算和避免除法可以加快算法速度。

   只需作以下变换：

   初值：

   $$Error=△y/△x-0.5$$

   经过简单变换：

   $$NError=2\cdot Error\cdot △x=2△y-△x$$

   便得到了整数算法。

3. 一般Bresenham算法

   为了使第一卦限的Bresenham算法适用于一般直线，进行如下改造：

   1. 当直线斜率$|k|>1$时，改为y的增量总为1，判断$x$是否需要增加1
   2. $x$或$y$的增量可能是1或-1，视直线所在象限决定。

圆光栅化算法

简单方程方法

圆的极坐标方程为：

$$\begin{gathered} x=R\cos \theta \\ y=R\sin \theta \end{gathered}$$

每次给 $\theta$ $\theta$${\theta }_{i+1}={\theta }_i+△\theta$

那么：

$$\begin{gathered} x_{i+1}=round(R\cos {\theta }_{i+1}) \\ {y}_{i+1}=round(R\sin {\theta }_{i+1}) \end{gathered}$$

利用圆的八方对称画圆

Bresenham画圆算法

以圆心为坐标原点，建立局部坐标系

先考虑第一象限的八分之一圆弧：

设$P_{i-1}(x_{i-1},y_{i-1})$为已确定的逼近像素点

当$x_i=x_{i-1}+1$时，要决定$y_i$的取值

令$E(\frac{R}{\sqrt{2}},\frac{R}{\sqrt{2}})$

$$\begin{gathered} D(S_i)=[(x_{i-1}+1{)}^2+y_{i-1}^2]-R^2 \\ D(T_i)=[(x_{i-1}+1{)}^2+(y_{i-1}-1{)}^2]-R^2 \end{gathered}$$

若$|D(S_i)|\ge |D(T_I)|$,则$T_i$比$S_i$更接近实际的圆弧， 应选$T_i$
反之，选择$S_i$。

令$d_i=|D(S_i)|-|D(T_i)|$

于是，$d_i\ge 0$时，选$T_i$，反之，选择$S_i$。

分析情况ABCDE，可以将$d_i$改写为：

$$\begin{array}{rl}{d}_i=& D(S_i)+D(T_i)\\ =& [(x_{i-1}+1{)}^2+y_{i-1}^2]-R^2+[(x_{i-1}+1{)}^2+(y_{i-1}-1{)}^2]-R^2\end{array}$$

用$i+1$代替上式中的$i$，得：

$$\begin{array}{rl}{d}_{i+1}=& [(x_i+1{)}^2+y_i^2]-R^2+[(x_i+1{)}^2+(y_i-1{)}^2]-R^2\end{array}$$

用$d_{i+1}-d_i$，得：

$$d_{i+1}-d_i=2[(x_i+1{)}^2-(x_{i-1}+1{)}^2]+(y_i^2-y_{i-1}^2)+(y_i-1{)}^2-(y_{i-1}-1{)}^2$$

改进：

若$d_i\ge 0,$选$T_i$，此时：

$$\begin{gathered} x_i=x_{i-1}+1 \\ {y}_i=y_{i-1}-1 \\ {d}_{i+1}=d_i+4(x_{i-1}-y_{i-1})+10 \end{gathered}$$

反之，选$S_i$，此时

$$\begin{gathered} x_i=x_{i-1}+1 \\ {y}_i=y_{i-1} \\ {d}_{i+1}=d_i+4x_{i-1}+6 \end{gathered}$$

$d_i$的初值$d_1$可以由$(1)$求出，将$i=1,x_0=0,y_0=R$带入，得：

$$d_1=3-2R$$

显然，改进方法的计算量更小，效率高。

中点圆算法

设$d$为点$p(x,y)$到圆心的距离，有：

$$d=F(x,y)=x^2+y^2-R^2$$

以圆的下 2个可选像素 中点的函数值 d的符号 决定选择 2个可选像素 T和 B中哪一个更接近圆而作为圆的显示点 ：

$$d_M=F(x_M,y_M)=F(x_p+1,y_p-0.5)=(x_p+1{)}^2+(y_p-0.5{)}^2-R^2$$

如果$d_M\le 0$，表示下一个中点M在圆内，用T逼近，得：

$$\begin{gathered} d_{MT}=F(x_{MT},y_{MT})=F(x_p+2,y_p-0.5)=(x_p+2{)}^2+(y_p-0.5{)}^2-R^2 \\ △d_{MT}=d_{MT}-d_M=2x_p+3 \end{gathered}$$

反之，表示下一中点M在园外，用B逼近，得：

$$\begin{gathered} d_{MB}=F(x_{MB},y_{MB})=F(x_p+2,y_p-1.5) \\ △d_{MB}=d_{MB}-d_M=2x_p-2y_p+5 \end{gathered}$$

综上，中点圆算法为：

根据中点d的值，决定显示的光栅点，更新$△d$$(△d_{MT}或{△}_{MB})$，更新d。

初值

由$x_0=0,y_0=R$
得$x_{M0}=0+1=1,y_{M0}=R-0.5$
$d_{M0}=F(x_{M0},y_{M0})=1.25-R$

中点圆整数算法

为了将其改造为整数计算，定义新变量：$D=d-0.25$
判别式$d<0$等价于$D<-0.25$
在D为整数的情况下，$D<-0.25$等价于$D<0$
仍将D写为d（新的初值$d=1-radius$)，可得到中点圆整数算法

椭圆光栅化算法

设椭圆方程为：

$$F(x,y)=b^2{x}^2+a^2{y}^2-a^2{b}^2=0$$

该椭圆上一点$(x,y)$处的法向量为：

$$N(x,y)=\frac{\partial F}{\partial x}i+\frac{\partial F}{\partial y}j=2b^{2}xi+2a^{2}yj$$

在上半部分，法向量y的分量更大而在下部分, 法向量的x分量更大, 因而, 在上部分若当前最佳逼近理想椭圆弧的像素(xP,yP)满足下列不等式：

$$b^2(x_p+1)<a^2(y_p-0.5)$$

在上半部分，假设横坐标为$x_p$的像素中，与椭圆弧更接近的点是$(x_p,y_p)$,那么下一对候选像素的中点为$(x_p+1,y_p-0.5)$,判别式为：

$$d_1=F(x_p+1,y_p-0.5)=b^2(x_p+1{)}^2+a^2(y_p-0.5{)}^2-a^2{b}^2$$

若$d_1<0$，中点在椭圆内，则取正右方像素，判别式更新：

$$d_1^{,}=F(x_p+2,y_p-0.5)$$

若$d_1\ge 0$，中点在椭圆外，此时取右下方像素，更新判别式：

$$d_1^{\prime }=F(x_p+2,y_p-1.5)$$

由于弧的起点为$(0,b)$，第一中点为$(1,b-0.5)$,对应判别式为：

$$d_{10}=F(1,b-0.5)$$

**在下部分，**改为从正下方和右下方两个像素选择下一像素，计算与上半部分类似。

基本多边形扫描转换与区域填充

多边形的扫描转换，主要通过确定穿越区域的扫描线覆盖区间来填充。

区域填充是从给定的位置开始涂描，直到指定的边界条件为止。

多边形的扫描转换

顶点表示：用多边形的顶点序列刻画多边形。

点阵表示：用位于多边形内的像素集合来刻画多边形。

扫描转换多边形：从多边形的顶点信息出发，求出位于其内部的各个像素，并将颜色值写入帧缓存中相应单元的过程。

基本问题有：

1. 如何判断一个点是否位于多边形区域内？

   点在多边形内的包含性检验方法：检验夹角之和、射线法检验交点数。

转角法：若夹角和为0，则点$p$在多边形外；若夹角和为360，则点$p$在多边形内。

射线法：交点数为偶数，点在多边形外；交点数为奇数，点在多边形之内。

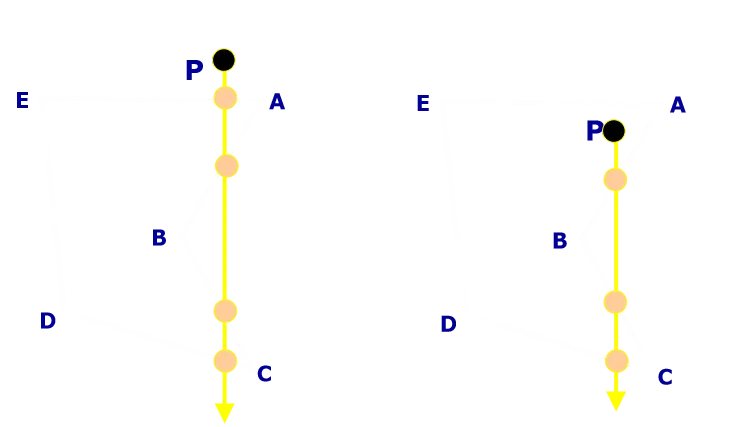
1. 逐点测试效率太低

采用包围盒法：对凸多边形效果好，但凹多边形效率仍然低下。

扫描线填充算法：

扫描线填充算法：按扫描线顺序，测试点的连贯性。

种子填充算法：从内部一个种子点出发，测试点的连贯性。

X-扫描线算法

基本思想：

按扫描线顺序，计算扫描线与多边形的相交区间；再用要求的颜色显示区间的所有像素。

算法步骤：

1. 确定多边形所占有的最大扫描线数，得到多边形顶点的最小、最大$y$值$(y_{min}和y_{max})$。
2. 从$y=y_{min}$到$y=y_{max}$，每次用一条扫描线进行填充。
3. 对一条扫描线填充的过程分为四个步骤：求交、排序、交点配对、区间填色。

取整规则

交点的取整规则：使生成的像素全部位于多边形之内。

为什么不采用四舍五入的规则？四舍五入可能导致部分像素位于多边形之外，从而不可用。

假定非水平边和扫描线y=e相交，交点横坐标为$x$，规则如下：

1. $x$为小数，即交点落在扫描线上两个相邻像素间时：

   1. 交点位于左边界上，向右取整。

   2. 交点位于右边界上，向左取整。

      

2. 边界上像素的取舍：为了避免填充扩大化，规定落在右边边界上的像素不予填充。

   • 具体实现时，对扫描线与多边形相交区间左闭右开。

     

3. 当扫描线与多边形顶点相交时：交点的取舍，保证交点正确配对。

   • 交点配对：当扫描线与多边形的顶点相交时：

     • 若共享顶点的两条边落在扫描线两边，交点只算一个。
     • 若共享顶点的两条边落在扫描线同一边，交点作为零或两个。

   • 实际处理中，只要检查顶点的两条边的另外两个端点的Y值，两个Y值中，大于交点Y值的个数为0\1\2，来决定取0\1\2个交点。

     

改进的有效边表算法（Y连贯性算法）

改进原理：

• 处理一条扫描线时，仅对有效边求交。
• 利用扫描线的连贯性。
• 利用多边形边的连贯性。

有效边：与当前扫描线相交的多边形的边，也称为活性边。
有效边表：把有效边按与扫描线交点x坐标递增的顺序存放在一个链表中，此链表称为有效边表。

有效边表中，每个结点的存储方式：

$$x{|}_{y_{min}}{y}_{max}\frac{1}{k}next$$

构造边表：

1. 首先构造一个纵向链表，链表的长度为多边形所占有的最大扫描线数，链表的每个结点，称为一个桶，对应多边形覆盖的每一条扫描线。

2. 将每条边的信息链入与该边最小y坐标（$y_{min}$ ）相对应的桶处。
   (也就是说，若某边的较低端点为$y_{min}$，则该边放在相应的扫描线桶中。）

3. 每条数据边形成一个结点，内容包括：

   1. 扫描线与该边的初始交点x（较低端点的x值）
   2. $\frac{1}{k}$
   3. 该边的最大$y$值$y_{max}$

4. 同一桶中，若干条边按$x$由小到大排序，若相等，按照$\frac{1}{k}$由小到大排序。

   

算法步骤：

1. 初始化：构造边表，AET表置空。
2. 将第一个不空的ET表中的边与AET表合并。
3. 由AET表中取出交点对进行填充。填充之后删除$y=y_{max}$的边。
4. $y_{i+1}=y_i+1$,根据$x_{i+1}=x_i+1/k$计算并修改AET表，同时合并ET表中$y=y_i+1$桶中的边，按次序插入到AET表中，形成新的AET表。
5. AET表不为空则转到3，否则end。

边缘填充算法

基本思想：按任意顺序，处理多边形的每条边。

处理时，先求出该边与扫描线的交点，再对扫描线上交点右方的所有像素取反。

算法简单，但对于复杂图形，每一个像素可能被访问多次。

栅栏填充算法

栅栏指的是一条过多边形顶点且与扫描线垂直的直线。它把多边形分为两半。

基本思想：按任意顺序处理多边形的每一条边，但处理每条边与扫描线的交点时，将交点与栅栏之间的像素取反。
这种算法尽管减少了被重复访问像素的数目，但仍有一些像素被重复访问。

边界标志算法

基本思想：先用特殊的颜色在帧缓存中将多边形的边界勾画出来，然后将着色的像素点依 x 坐标递增的顺序配对，再把每一对像素构成的区间置为填充色。
分为两个步骤：打标记-多边形扫描转化（利用直线的扫描转换实现），填充。

当用软件实现本算法时，速度与改进的有效边表算法相当，但本算法用硬件实现后速度会有很大提高

区域填充

基本概念：从区域内的某一个像素点（种子点）开始，由内向外将填充色扩展到整个区域内的过程
区域：已经表示成点阵形式的填充图形，它是相互连通的一组像素的集合。

边界表示法：把位于给定区域的边界上的像素一一列举出来的方法。
边界表示法中，由于边界由特殊颜色指定，填充算法可以逐个像素地向外处理，直到遇到边界颜色为止，这种方法称为边界填充算法。

内点表示法：枚举出给定区域内所有像素的表示方法。

以内点表示法为基础的区域填充算法称为泛填充算法。

4连通区域、8连通区域：

连通性：4连通可看作8连通区域，但对边界有要求。

边界填充算法

算法的输入：种子点坐标(x,y)，填充色以及边界颜色。

利用堆栈实现简单的种子填充算法。

• 算法从种子点开始检测相邻位置是否是边界颜色。
• 若不是就用填充色着色。
• 检测该像素点的相邻位置。
• 直到检测完区域边界颜色范围内的所有像素为止。

特点：

• 可以用于填充带有内孔的平面区域。
• 把太多的像素压入堆栈，降低了效率，同时需要较大的存储空间。
• 递归执行，算法简单，但效率不高，区域内每一像素都引起一次递归，进/出栈费时费内存。
• 通过沿扫描线填充水平像素段，来代替处理4-邻接点和8-邻接点。

扫描线种子算法

扫描线通过在任意不间断扫描线区间中只取一个种子像素的方法使堆栈的尺寸极小化。
不间断区间是指在一条扫描线上的一组相邻像素。

基本过程：当给定种子点时，首先填充种子点所在的扫描线上的位于给定区域的一个区段，然后确定与这一区段相通的上下两条扫描线上位于给定区域内的区段，并依次保存下来，重复以上过程。

算法步骤：在任意一个扫描线与多边形的相交区间中, 只取一个种子像素, 并将种子像素入栈, 当栈非空时作如下四步操作:

1. 栈顶像素出栈
2. 沿扫描线对出栈像素的左右像素进行填充, 直至遇到边界像素为止, 也就是对包含出栈像素的整个区间进行填充
3. 上述区间内最左最右的像素分别记为xl和xr
4. 在区间［xl, xr］中检查与当前扫描线相邻的上下两条扫描线的有关像素是否全为边界像素或已填充的像素, 若存在非边界、 非填充的像素, 则把每一区间的最右像素入栈。

字符处理

ASCII码：“美国信息交换用标准代码集”(American Standard Code for Information Interchange)

国际码：“中华人民共和国国家标准信息交换编码，简称为国际码，代号GB2312－80

字库：字库中储存了每个字符的图形信息

点阵字符

在点阵表示中，每个字符由一个点阵位图来表示，显示时，形成字符的像素图案。

特点： 定义和显示直接、简单、存储需要耗费大量空间。

改进：从一组点阵字符生成不同尺寸和不同字体的其他字符、采用压缩技术。

矢量字符

矢量字符采用直线和曲线段来描述字符形状，矢量字符库中记录的是笔划信息；显示时：解释字符的每个笔划信息。

轮廓字型法采用直线或二、三次曲线的集合来描述一个字符的轮廓线，轮廓线构成了一个或若干个封闭区域，显示时只要填充这些区域就可产生相应的字符

• 显示时可以“无极放缩”
• 占用空间少，美观，变换方便

属性处理

图素或图段的外观由其属性决定。

图形软件中实现属性选择的方法是提供一张系统当前属性值表，通过调用标准函数提供属性值表的设置和修改。进行扫描转换时，系统使用属性值表中的当前属性值进行显示和输出。

线宽

线刷子：垂直刷子、水平刷子

线刷子特点：

• 实现简单、效率高
• 斜线与水平(或垂直)线不一样粗
• 当线宽为偶数个像素时，线的中心将偏移半个像素
• 利用线刷子生成线的始末端总是水平或垂直的，看起来不太自然

解决方法：添加线帽

方帽：调整端点位置，使粗线的显示具有垂直于线段路径的正方形端点。

凸方帽：简单将线向两头延伸一半线宽并添加方帽。

圆帽：通过对每个方帽添加一个填充的半圆得到。

当比较接近水平的线与比较接近垂直的线汇合时，汇合处外角将有缺口。

解决方法：斜角连接、圆角连接、斜切连接。

方刷子：

方刷子绘制的线条（斜线）比用线刷子所绘制的线条要粗一些，斜线与水平（或垂直）线不一样粗。线条自然地带有一个“方线帽”。

利用像素模板进行线宽处理：

用等距线方法:
线宽均匀、端口处与边垂直、生成的图形质量高。

线型

用位屏蔽器实现

位屏蔽器中每一位对应的是一个像素，而不是单位长度，不能满足要求
线型中的笔划长度与直线长度有关
斜线笔划长度比水平或垂直线笔划长
对工程图，这种变化是不允许的，不符合国标规定

用像素段方法实现：针对不同的线型，画线程序沿路径输出一些连续像素段，在每两个实心段之间有一段中间空白段，他们的长度（像素数目）可用像素模板(pixel mask)指定
如何保证任何方向的划线长度近似相等呢？

• 可根据线的斜率来调整实心段和中间空白段的像素数目。

曲线的线性和线宽

采用像素模板的方法对圆的线型处理：

• 从一个八分象限转入下一个八分象限时要交换像素的位置，以保持划线长度近似相等。
• 在沿圆周移动时调整画每根划线的像素数目以保证划线长度近似相等。
• 改进：采用沿等角弧画像素代替用等长区间的像素模板来生成等长划线。

曲线的线宽

线刷子：经过曲线斜率为1和-1处，必须切换刷子
（曲线接近水平与垂直的地方，线条更粗）

方刷子：接近水平垂直的地方，线条更细
（要显示一致的曲线宽度可通过旋转刷子方向以使其在沿曲线移动时与斜率方向一致）

圆弧刷子：采用填充方法

区域填充属性

区域填充属性选择包括颜色、图案和透明度。

确定区域与模板之间的位置关系（对齐方式）

反走样

用离散量表示连续量引起的失真，就叫做走样。

产生原因：数学意义上的图形是由无限多个连续的、面积为零的点构成；
光栅显示器上，用有限多个离散的，具有一定面积的像素来近似地表示他们

走样现象：

1. 光栅图形产生的阶梯形
2. 图形中包含相对微小的物体时

用于减少或消除这种效果的技术，称为反走样

简单的方法：过取样（后滤波）、区域取样（前滤波）

分辨率提高一倍，阶梯程度减小一倍

过取样

在高于显示分辨率的较高分辨率下用点取样方法计算，然后对几个像素的属性进行平均得到较低分辨率下的像素属性。

简单过取样：在x，y方向把分辨率都提高一倍，使每个像素对应4个子像素，然后扫描转换求得各子像素的颜色亮度，再对4个像素的颜色亮度进行平均，得到较低分辨率下的像素颜色亮度。。

重叠过取样

为了得到更好的效果，在对一个像素点进行着色处理时，不仅仅只对其本身的子像素进行采样，同时对其周围的多个像素的子像素进行采样，来计算该点的颜色属性

基于加权模板的过取样

前面在确定像素的亮度时，仅仅是对所有子像素的亮度进行简单的平均。更常见的做法是给接近像素中心的子像素赋予较大的权值，即对所有子像素的亮度进行加权平均。

简单的区域取样

在整个像素区域内进行采样，这种技术称为区域取样。

由于像素的亮度是作为一个整体被确定的，不需要划分子像素，故也被称为前置滤波。

如何计算直线段与像素相交区域的面积？

1. 将屏幕像素分割成n个更小的子像素
2. 计算中心落在直线段内的子像素的个数m
3. m/n为线段与像素相交区域面积的近似值。

在过取样中，我们对所有子像素的亮度进行简单平均或加权平均来确定像素的亮度。

在区域取样中，我们使用覆盖像素的连续的加权函数（Weighting Function）或滤波函数(Filtering Function)来确定像素的亮度。

将加权函数在整个二维显示图形上积分，得到具有一定体积的滤波器（Filter），该滤波器的体积为1
将加权函数在显示图形上进行积分，得到滤波器的一个子体，该子体的体积介于0到1之间，用它来表示像素的亮度。

特点：

接近理想直线的像素将被分配更多的灰度值。
相邻两个像素的滤波器相交，有利于缩小直线条上相邻像素的灰度差。