6.9.单源最短路径问题-BFS算法
一.前言:

问题1:
以上述图片为例,比如从G港到Y城,可以是G港->R城->Y城,也可以是G港->P城->Y城等,有很多条路径都可以实现从G港到Y城,但要从中找出G港到Y城距离最短的那一条路径,这就是单源最短路径问题。
单源最短路径问题就是只有一个源头,从该源头出发,到达其他任意一个顶点可以走的最短路径。
对于单源最短路径的题型,需要掌握BFS算法(可以求无权图的单源最短路径)和Dijkstra算法(可以求带权图和无权图的单源最短路径)。
问题2:
上述图片的各个城市需要往来,相互之间怎么走距离最近呢?比如R城和M城之间要走哪条路比较划算即距离最近,Y城和P城之间要走哪条路比较划算即距离最近,所以在这样的应用场景之下,我们就要确定每对顶点间的最短路径。
对于各顶点间的最短路径的题型,需要掌握Floyd算法(可以求带权图和无权图的各顶点间的最短路径)。
二.BFS算法求无权图的单源最短路径的准备工作:
1.注意:无权图可以视为一种特殊的带权图,只是每条边的权值都为1或者权值都一样的边

2.实例:

以上述图片为例,从2号顶点出发,求出到达各个顶点的最短路径,如下图:

如上图,通过BFS算法,从2号顶点出发,可以找到与2号顶点相邻的的顶点即1、6号顶点,2号顶点与1、6号顶点之间的距离都是1(无向图的边的权值可以视为1),如下图:

如上图,通过1、6号顶点可以找到5、3、7号顶点,2号顶点到达5、3、7号顶点的最短路径都是2,如下图:

如上图,继续往下找可以找到4、8号顶点,2号顶点到达4、8号顶点的最短路径都是3,如下图:

所以对上述图片里的图执行一次BFS算法即广度优先遍历,就可以得到2号顶点到达其他所有顶点的最短路径。
三.BFS算法求无权图的单源最短路径的代码实现:
1.代码:

如上图,需要在原有的BFS算法的代码上进行改造->在BFS函数中用visit函数来抽象地表示出对某一个顶点的访问,改造成求最短路径,只需要把visit函数的作用进行改造即可,如下图:

上述图片的代码解读:
-
BFS_MIN_Distance函数的第一个形参Graph G表示图,第二个形参int u表示当前顶点的编号,G.vexnum表示图的顶点个数;
-
d[]数组用来记录起始顶点到各个顶点的最短路径的长度;path[]数组用来记录每一个顶点在这个最短路径上的直接前驱,path数组就是记录这条最短路径是从哪个顶点过来的;
2.举例:

如上图,以2号顶点为例,求2号顶点到达其他顶点的最短路径->
BFS_MIN_Distance函数的第一个形参Graph G表示图,第二个形参int u表示当前顶点的编号,
由于此时操作的是2号顶点,因此BFS_MIN_Distance函数的第二个形参u等于2;
d[]数组用来记录起始顶点到各个顶点的最短路径的长度;path[]数组用来记录每一个顶点在这个最短路径上的直接前驱,path数组就是记录这条最短路径是从哪个顶点过来的,
由于一开始并不知道顶点间的距离和顶点前驱,因此第一个for循环把d数组的值都初始化为无穷,path数组的值都初始化为-1,
d[u]就是起始顶点到第u号顶点的最短路径,由于2号顶点是起始顶点,第u号顶点也是2号顶点,2号顶点到2号顶点的最短路径为0,因此d[2]=0;
visited[u]=true表示第u号顶点已经被访问过,EnQueue(Q,u)函数代表第u号顶点进入队列Q,
此时就是visited[2]=true即2号顶点被访问过,并把第2号顶点放入队列Q中,如下图:

如上图,继续判断是否执行while循环,
Q队列为空时isEmpty(Q)的值为true,Q队列非空时isEmpty(Q)的值为false,
由于此时队列Q中有2号顶点即Q队列非空,因此isEmpty(Q)的值为false,!isEmpty(Q)的值为true,
此时执行while循环,首先执行DeQueue(Q,u)函数弹出队头元素即弹出第u号顶点,此时是弹出第2号顶点,如下图:

如上图,接下来执行while循环里的for循环,for循环可以找到与第u号顶点相邻的所有顶点,此时就是找到与2号顶点相邻的所有顶点,现在可以找到1、6号顶点,以1号顶点为例,此时w为1,
如果其中的某个顶点即w号顶点没有被访问过即对应的visited值为false,!visited[w]为true,那么就会执行if语句,由于此时w为1,1号顶点没有被访问过,因此执行if语句,
d[w]=d[u]+1意味着当前顶点即第u号顶点到达相邻顶点即第w号顶点的最短路径加1,此时就是d[1]=d[2]+1,由于d[2]为0,那么d[1]为1,意味着从2号顶点到1号顶点的最短路径为1,
还需要修改path数组的值,path数组就是记录这条最短路径是从哪个顶点过来的,1号顶点是从2号顶点过来的,所以1号顶点的直接前驱是2号顶点即path[1]=2,
访问过的顶点visited的值修改为true,即visited[1]=true,
执行EnQueue(Q,w)让第w号顶点入Q队列,此时让1号顶点入Q队列,
同理,d[6]为1,path[6]=2,visited[6]=true,6号顶点入Q队列,
至此2号顶点处理完毕,如下图:

如上图,继续判断是否执行while循环,
Q队列为空时isEmpty(Q)的值为true,Q队列非空时isEmpty(Q)的值为false,
由于此时队列Q中有1、6号顶点即Q队列非空,因此isEmpty(Q)的值为false,!isEmpty(Q)的值为true,
此时执行while循环,首先执行DeQueue(Q,u)函数弹出队头元素即弹出第u号顶点,此时是弹出第1号顶点(注:虽然一开始u是第2号顶点,但DeQueue函数中的具体内容已经把u的赋值操作完成了即把2改为1,就是把队头元素即第1号顶点弹出队列,之后的u就代表当前顶点即1号顶点),
开始操作第1号顶点->
如上图,接下来执行while循环里的for循环,for循环可以找到与第u号顶点相邻的所有顶点,此时就是找到与1号顶点相邻的所有顶点,现在可以找到2、5号顶点,第一个找到的是2号顶点,由于2号顶点已经被访问过,因此不会执行if语句,会跳过2号顶点,
第二个找到的是5号顶点,此时w为5,
如果其中的某个顶点即w号顶点没有被访问过即对应的visited值为false,!visited[w]为true,那么就会执行if语句,由于此时w为5,5号顶点没有被访问过,因此执行if语句,
d[w]=d[u]+1意味着当前顶点即第u号顶点到达相邻顶点即第w号顶点的最短路径加1,此时就是d[5]=d[1]+1,由于d[1]为1,那么d[5]为2,意味着从2号顶点到5号顶点的最短路径为2,
还需要修改path数组的值,path数组就是记录这条最短路径是从哪个顶点过来的,5号顶点是从1号顶点过来的,所以5号顶点的直接前驱是1号顶点即path[5]=1,
访问过的顶点visited的值修改为true,即visited[5]=true,
执行EnQueue(Q,w)让第w号顶点入Q队列,此时让5号顶点入Q队列,
至此1号顶点处理完毕,如下图:

如上图,继续判断是否执行while循环,
Q队列为空时isEmpty(Q)的值为true,Q队列非空时isEmpty(Q)的值为false,
由于此时队列Q中有6、5号顶点即Q队列非空,因此isEmpty(Q)的值为false,!isEmpty(Q)的值为true,
此时执行while循环,首先执行DeQueue(Q,u)函数弹出队头元素即弹出第u号顶点,此时是弹出第6号顶点(注:虽然一开始u是第1号顶点,但DeQueue函数中的具体内容已经把u的赋值操作完成了即把1改为6,就是把队头元素即第6号顶点弹出队列,之后的u就代表当前顶点即6号顶点),
开始操作第6号顶点->
如上图,接下来执行while循环里的for循环,for循环可以找到与第u号顶点相邻的所有顶点,此时就是找到与6号顶点相邻的所有顶点,现在可以找到2、3、7号顶点,第一个找到的是2号顶点,由于2号顶点已经被访问过,因此不会执行if语句,会跳过2号顶点,
第二个找到的是3号顶点,此时w为3,
如果其中的某个顶点即w号顶点没有被访问过即对应的visited值为false,!visited[w]为true,那么就会执行if语句,由于此时w为3,3号顶点没有被访问过,因此执行if语句,
d[w]=d[u]+1意味着当前顶点即第u号顶点到达相邻顶点即第w号顶点的最短路径加1,此时就是d[3]=d[6]+1,由于d[6]为1,那么d[3]为2,意味着从2号顶点到3号顶点的最短路径为2,
还需要修改path数组的值,path数组就是记录这条最短路径是从哪个顶点过来的,3号顶点是从6号顶点过来的,所以3号顶点的直接前驱是6号顶点即path[3]=6,
访问过的顶点visited的值修改为true,即visited[3]=true,
执行EnQueue(Q,w)让第w号顶点入Q队列,此时让3号顶点入Q队列,
同理,d[7]为2,path[7]=6,visited[7]=true,7号顶点入Q队列,
至此6号顶点处理完毕,如下图:

如上图,继续判断是否执行while循环,
Q队列为空时isEmpty(Q)的值为true,Q队列非空时isEmpty(Q)的值为false,
由于此时队列Q中有5、3、7号顶点即Q队列非空,因此isEmpty(Q)的值为false,!isEmpty(Q)的值为true,
此时执行while循环,首先执行DeQueue(Q,u)函数弹出队头元素即弹出第u号顶点,此时是弹出第5号顶点(注:虽然一开始u是第6号顶点,但DeQueue函数中的具体内容已经把u的赋值操作完成了即把6改为5,就是把队头元素即第5号顶点弹出队列,之后的u就代表当前顶点即5号顶点),
开始操作第5号顶点->
如上图,接下来执行while循环里的for循环,for循环可以找到与第u号顶点相邻的所有顶点,此时就是找到与5号顶点相邻的所有顶点,现在可以找到1号顶点,由于1号顶点已经被访问过,因此不会执行if语句,会跳过1号顶点,
至此5号顶点处理完毕,如下图:

如上图,继续判断是否执行while循环,
Q队列为空时isEmpty(Q)的值为true,Q队列非空时isEmpty(Q)的值为false,
由于此时队列Q中有3、7号顶点即Q队列非空,因此isEmpty(Q)的值为false,!isEmpty(Q)的值为true,
此时执行while循环,首先执行DeQueue(Q,u)函数弹出队头元素即弹出第u号顶点,此时是弹出第3号顶点(注:虽然一开始u是第5号顶点,但DeQueue函数中的具体内容已经把u的赋值操作完成了即把5改为3,就是把队头元素即第3号顶点弹出队列,之后的u就代表当前顶点即3号顶点),
开始操作第3号顶点->
如上图,接下来执行while循环里的for循环,for循环可以找到与第u号顶点相邻的所有顶点,此时就是找到与3号顶点相邻的所有顶点,现在可以找到4、6、7号顶点,
第一个找到的是4号顶点,此时w为4,
如果其中的某个顶点即w号顶点没有被访问过即对应的visited值为false,!visited[w]为true,那么就会执行if语句,由于此时w为4,4号顶点没有被访问过,因此执行if语句,
d[w]=d[u]+1意味着当前顶点即第u号顶点到达相邻顶点即第w号顶点的最短路径加1,此时就是d[4]=d[3]+1,由于d[3]为2,那么d[4]为3,意味着从2号顶点到4号顶点的最短路径为3,
还需要修改path数组的值,path数组就是记录这条最短路径是从哪个顶点过来的,4号顶点是从3号顶点过来的,所以4号顶点的直接前驱是3号顶点即path[4]=3,
访问过的顶点visited的值修改为true,即visited[4]=true,
执行EnQueue(Q,w)让第w号顶点入Q队列,此时让4号顶点入Q队列,
之后依次找到的是6、7号顶点,由于6、7号顶点已经被访问过,因此不会执行if语句,会跳过6、7号顶点,
至此3号顶点处理完毕,如下图:

如上图,继续判断是否执行while循环,
Q队列为空时isEmpty(Q)的值为true,Q队列非空时isEmpty(Q)的值为false,
由于此时队列Q中有7、4号顶点即Q队列非空,因此isEmpty(Q)的值为false,!isEmpty(Q)的值为true,
此时执行while循环,首先执行DeQueue(Q,u)函数弹出队头元素即弹出第u号顶点,此时是弹出第7号顶点(注:虽然一开始u是第3号顶点,但DeQueue函数中的具体内容已经把u的赋值操作完成了即把3改为7,就是把队头元素即第7号顶点弹出队列,之后的u就代表当前顶点即7号顶点),
开始操作第7号顶点->
如上图,接下来执行while循环里的for循环,for循环可以找到与第u号顶点相邻的所有顶点,此时就是找到与7号顶点相邻的所有顶点,现在可以找到3、4、6、8号顶点,前三次依次找到的是3、4、6号顶点,由于3、4、6号顶点已经被访问过,因此不会执行if语句,会跳过3、4、6号顶点,
第四个找到的是8号顶点,此时w为8,
如果其中的某个顶点即w号顶点没有被访问过即对应的visited值为false,!visited[w]为true,那么就会执行if语句,由于此时w为8,8号顶点没有被访问过,因此执行if语句,
d[w]=d[u]+1意味着当前顶点即第u号顶点到达相邻顶点即第w号顶点的最短路径加1,此时就是d[8]=d[7]+1,由于d[7]为2,那么d[8]为3,意味着从2号顶点到8号顶点的最短路径为3,
还需要修改path数组的值,path数组就是记录这条最短路径是从哪个顶点过来的,8号顶点是从7号顶点过来的,所以8号顶点的直接前驱是7号顶点即path[8]=7,
访问过的顶点visited的值修改为true,即visited[8]=true,
执行EnQueue(Q,w)让第w号顶点入Q队列,此时让8号顶点入Q队列,
至此7号顶点处理完毕,如下图:
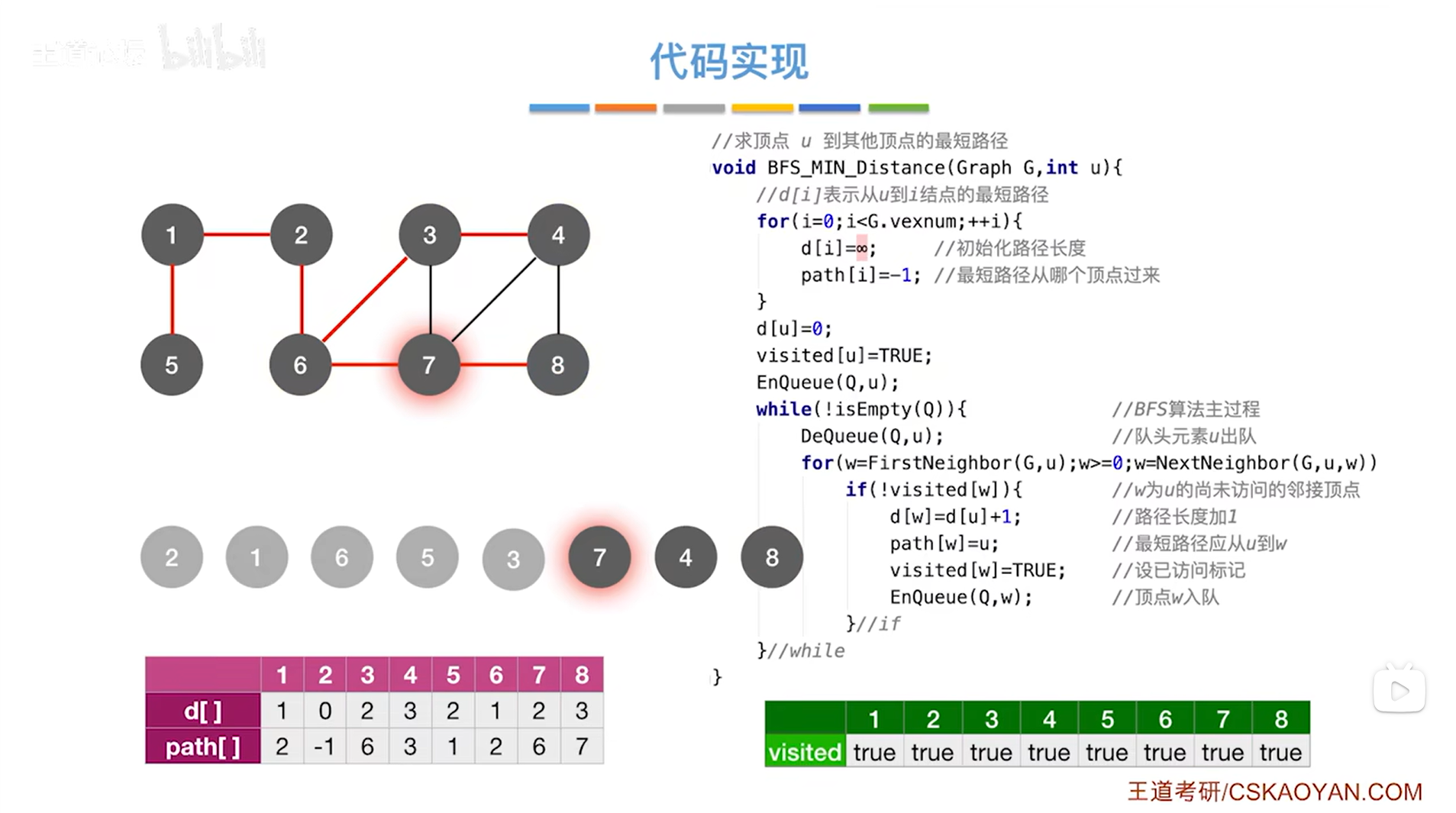
如上图,继续判断是否执行while循环,
Q队列为空时isEmpty(Q)的值为true,Q队列非空时isEmpty(Q)的值为false,
由于此时队列Q中有4、8号顶点即Q队列非空,因此isEmpty(Q)的值为false,!isEmpty(Q)的值为true,
此时执行while循环,首先执行DeQueue(Q,u)函数弹出队头元素即弹出第u号顶点,此时是弹出第4号顶点(注:虽然一开始u是第7号顶点,但DeQueue函数中的具体内容已经把u的赋值操作完成了即把7改为4,就是把队头元素即第4号顶点弹出队列,之后的u就代表当前顶点即4号顶点),
开始操作第4号顶点->
如上图,接下来执行while循环里的for循环,for循环可以找到与第u号顶点相邻的所有顶点,此时就是找到与4号顶点相邻的所有顶点,现在可以找到3、7、8号顶点,由于3、7、8号顶点都已经被访问过,因此都不会执行if语句,会跳过3、7、8号顶点,
至此4号顶点处理完毕,如下图:

如上图,继续判断是否执行while循环,
Q队列为空时isEmpty(Q)的值为true,Q队列非空时isEmpty(Q)的值为false,
由于此时队列Q中有8号顶点即Q队列非空,因此isEmpty(Q)的值为false,!isEmpty(Q)的值为true,
此时执行while循环,首先执行DeQueue(Q,u)函数弹出队头元素即弹出第u号顶点,此时是弹出第8号顶点(注:虽然一开始u是第4号顶点,但DeQueue函数中的具体内容已经把u的赋值操作完成了即把4改为8,就是把队头元素即第8号顶点弹出队列,之后的u就代表当前顶点即8号顶点),
开始操作第8号顶点->
如上图,接下来执行while循环里的for循环,for循环可以找到与第u号顶点相邻的所有顶点,此时就是找到与8号顶点相邻的所有顶点,现在可以找到4、7号顶点,由于4、7号顶点都已经被访问过,因此都不会执行if语句,会跳过4、7号顶点,
至此8号顶点处理完毕,如下图:

如上图,继续判断是否执行while循环,
Q队列为空时isEmpty(Q)的值为true,Q队列非空时isEmpty(Q)的值为false,
由于此时队列Q中没有顶点即Q队列为空,因此isEmpty(Q)的值为true,!isEmpty(Q)的值为false,
此时不再执行while循环了,至此BFS_MIN_Distance函数结束,
如下图:

如上图,最终得到了从2号顶点出发,到达其他所有顶点的最短路径长度,还有最短路径中完整的路径信息即path数组。
3.代码核心:该算法的核心就是BFS算法,只不过在BFS算法上增加了d数组和path数组,对于d数组和path数组的使用如下
以刚才的例子为例,如下图:

如上图,比如要想知道2号顶点到8号顶点的最短路径的信息,只需要找到8号顶点对应的d数组和path数组即可,
从d数组可以得知从2号顶点到8号顶点的最短路径长度为3,
通过path数组可以得知8号顶点的前驱是7号顶点,7号顶点的前驱是6号顶点,6号顶点的前驱是2号顶点,最终逆向找到了最原始的起点即找到了2号顶点,因此这条最短路径就是2->6->7->8,如下图:

如上图,上述图片里的图可以得出一个广度优先生成树,如下图,
通过观察可以发现,各个顶点在树的第几层,也直接的反映了从起点2到达其他顶点的最短路径是多少,因为该广度优先生成树是通过BFS算法得出的,那么该生成树的深度(高度)也一定是最小的,
比如8号顶点在树的第四层,那么2号顶点到达8号顶点的最短路径长度为3,最短路径是2->6->7->8:

