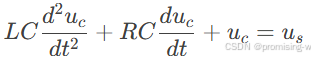信号与系统第二章学习(五)
第二章 连续系统的时域分析

2.1连续系统的建立——电路图建立微分方程

本章研究对象就是线性时不变连续系统
Z2.1连续系统的描述:电路图建立微分方程
1.数学模型

1. 电路分析
考虑一个简单的RLC串联电路,包含电阻 RR、电感 LL 和电容 CC。根据基尔霍夫电压定律,电路中的总电压降等于激励电压 us(t)us(t)。因此,我们可以写出:
其中:
是电阻上的电压,
是电感上的电压,
是电容上的电压。
2. 元件电压-电流关系
根据电路元件的电压-电流关系:
电阻:
电感:
电容:
3. 代入KVL方程
将元件的电压-电流关系代入KVL方程:
4. 微分方程
为了消除积分,我们对整个方程对时间 t 求导:
由于
,我们可以将
用
表示:
简化后得到:
这就是第一个方程:
5. 初始条件
初始条件
分别表示电容电压及其一阶导数在
时刻的值。
6. 一般形式的微分方程
将上述方程写成一般形式的二阶常系数线性微分方程:
其中:
这就是第二个方程。
总结
通过基尔霍夫电压定律和元件的电压-电流关系,我们得到了描述RLC电路行为的二阶常系数线性微分方程。这个方程可以用来分析电路在不同激励下的响应。
2.相似系统
相似系统:能用相同方程描述的系统。

Z2.2 微分方程的模拟框图
1.基本部件

基本运算:数乘、微分、相加
基本部件:加法器、数乘器(放大器)、积分器
- 加法器:

- 数乘器:

- 积分器:积分器的抗干扰比微分器好

2.模拟框图
模拟框图:将微分方程用基本部件的相互连接表征出来的图,简称框图。


绘制步骤为:
- 先画出两个积分器;
- 以最后一个积分器的输出端为y(t);
- 左边第一个积分器的输入端就是y''(t), 也是加法器的输出。

引入辅助函数 x(t)x(t) 的目的是为了简化原微分方程的处理,特别是当方程的右边包含输入函数 f(t)f(t) 的导数时。以下是详细解释为什么辅助函数要那样列方程:
1. 原方程的复杂性
原方程为:
这个方程的右边包含了 f(t) 的导数 f′(t),这使得直接求解y(t) 变得复杂,因为我们需要处理 f′(t) 的影响。
2. 引入辅助函数的目的
为了简化问题,我们引入一个辅助函数x(t),使得:
这个方程描述了一个更简单的系统,其输入是 f(t),输出是x(t)。通过这种方式,我们可以将原方程中的 f(t) 和 f′(t)的影响分离出来。
3. 表达 y(t) 与 x(t) 的关系
假设 y(t)可以表示为 x(t)及其导数的线性组合:
这个假设基于原方程中 f(t)和 f′(t) 的系数。通过这种表示,我们可以将 y(t) 的表达式中包含 f′(t)的部分转化为 x′(t)。
4. 验证关系的正确性
为了验证这个假设的正确性,我们将 y(t)=4x′(t)+x(t) 代入原方程:
y′′(t)+3y′(t)+2y(t)=4f′(t)+f(t)
通过一系列的推导和简化,我们发现这个假设是成立的。这表明通过引入辅助函数 x(t),我们可以将原方程转化为一个更易处理的形式。
5. 简化系统分析
通过引入辅助函数x(t),我们将原系统分解为两个部分:
一个子系统,其输入为f(t),输出为x(t)。
另一个子系统,其输入为x(t) 和 x′(t),输出为 y(t)=4x′(t)+x(t)。
这种分解使得我们可以分别分析和处理每个子系统,从而简化了整个系统的分析和设计。
总结
引入辅助函数 x(t)x(t) 的目的是为了将原方程中的复杂项(特别是f′(t))分离出来,使得我们可以更容易地处理和分析系统。通过这种方式,我们可以将原系统分解为更简单的子系统,从而简化整个系统的分析和设计过程。