数据结构实验6.1：矩阵的螺旋方阵输出

---

一，实验目的

1. 深入理解数组的存储结构与操作原理，熟练掌握矩阵的基本运算规则，包括矩阵的加法、乘法等，能够运用数组准确表示矩阵并实现相关运算，提升对数据结构中基础内容的应用能力。
2. 全面掌握稀疏矩阵的三元组表示方法，清晰理解其存储原理，包括非零元素的行、列和值如何在三元组中记录，能够灵活运用该表示方法对稀疏矩阵进行高效存储与操作。
3. 熟练掌握基于稀疏矩阵三元组表示的各种运算，如矩阵的转置、加法、乘法等，通过实际编程实现这些运算，深入体会稀疏矩阵在节省存储空间和提高运算效率方面的优势，增强对复杂数据结构运算的编程实现能力。

二，问题描述

已知一个6×6的螺旋方阵如下，编程实现输出n×n（n<20）阶的螺旋方阵（逆时针方向旋转）。

三，基本要求

• 定义螺旋方阵数据结构：使用二维数组作为存储螺旋方阵的基本数据结构，例如 int matrix[n][n]，其中 n 为方阵的阶数。该二维数组能够直观地表示方阵中每个位置的元素，方便后续对元素的访问和修改操作。同时，可考虑辅助使用一些变量，如记录当前填充位置的行索引 row、列索引 col 等，来帮助在填充过程中准确控制元素的位置。
• 设计求解螺旋方阵的算法，要进行算法分析：
  • 算法设计：从方阵的左上角开始，按照逆时针方向逐层填充数字。使用四个循环分别控制每一圈中左、下、右、上四个方向的数字填充。在填充每一圈时，先填充左边的列（从上到下），再填充下边的行（从左到右），接着填充右边的列（从下到上），最后填充上边的行（从右到左）。每填充完一圈，更新下一圈的起始位置和结束条件。
  • 算法分析：时间复杂度方面，由于要填充n×n个元素，每个元素填充操作的时间基本固定，所以总的时间复杂度为 $O(n^2)$ 。空间复杂度上，除了输入的n×n阶二维数组用于存储螺旋方阵外，仅使用了少量辅助变量（如行索引、列索引等），辅助变量占用空间与n无关，因此空间复杂度为 $O(n^2)$ 。
• 在参考程序的下划线处填入适当的语句：仔细阅读参考程序，根据程序的逻辑结构和已有的代码上下文，准确理解每个下划线处的功能需求。通过分析算法步骤和数据流向，确定需要填入的语句，可能涉及变量的赋值、循环条件的设置、数组元素的操作等，确保填入的语句能够使程序正确实现螺旋方阵的生成功能。
• 上机调试、测试，保存并打印测试结果，对结果进行分析：在集成开发环境中输入编写好的代码，进行编译和调试，利用断点、输出中间变量值等调试手段，排查程序中可能存在的语法错误和逻辑错误。设计多种测试用例，包括n取较小值（如2、3）和较大值（接近20）的情况，观察程序输出的螺旋方阵是否符合预期。将测试结果保存并打印出来，从正确性（方阵元素是否按逆时针螺旋规律排列）、效率（程序运行时间是否在可接受范围内，特别是当n增大时）等方面对结果进行分析，针对发现的问题进一步优化程序。

四，算法分析

• 可用一个二维数组来保存n阶螺旋方阵：二维数组具有直观的行列结构，与螺旋方阵的布局相契合，能够方便地通过行列索引访问和修改方阵中的元素。例如，对于方阵中第 i 行第 j 列的元素，可直接通过 matrix[i][j] 进行操作，这种数据结构选择为螺旋方阵的生成和后续处理提供了便利的基础。
• 一个n阶的螺旋方阵共有(n+1)/2圈，因是逆时针旋转，每一圈应先产生左方的数字，再产生下方的数字，第三产生右方的数字，最后产生上方的数字，注意控制好每一圈各方产生的数字长度：对于n阶螺旋方阵，从最外层开始，每向内一层，边长减2，通过数学推导可得圈数为(n+1)/2 。在填充每一圈时，按照逆时针顺序，先确定左边列的填充范围（从上到下，列索引固定，行索引变化），再确定下边行的填充范围（从左到右，行索引固定，列索引变化），接着确定右边列的填充范围（从下到上，列索引固定，行索引变化），最后确定上边行的填充范围（从右到左，行索引固定，列索引变化）。通过合理设置循环条件和索引变化规则，精确控制每一圈各方产生的数字长度，确保螺旋方阵能够正确生成。

五，实验操作

1，双击Visual Studio程序快捷图标，启动程序。

2，之前创建过项目的话，直接打开即可，这里选择【创建新项目】。

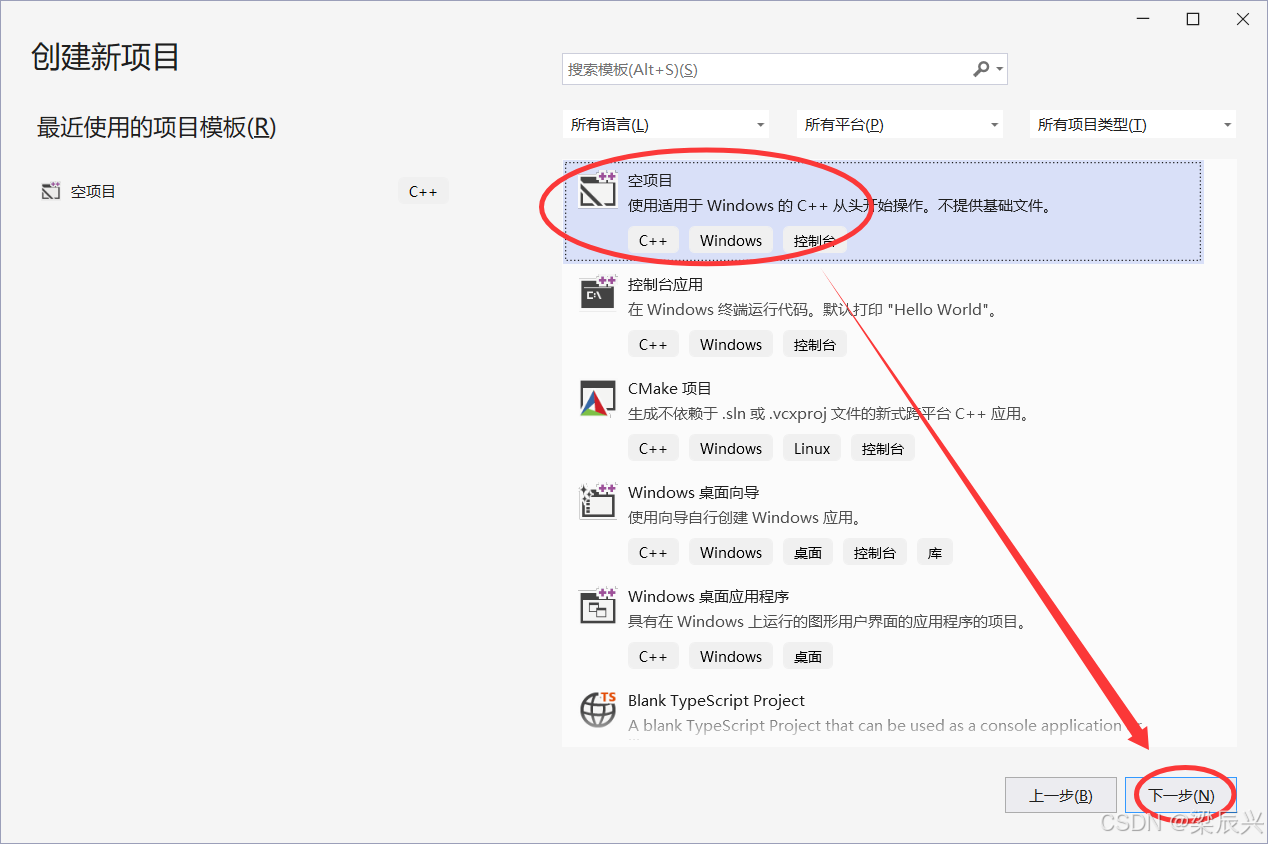
3，单击选择【空项目】——单击【下一步】按钮。

4，编辑好项目的名称和存放路径，然后单击【创建】按钮。

5，创建C++程序文件，右击【源文件】——选择【添加】——【新建项】。

6，输入项目名称，单击【添加】按钮。

7，编写代码，单击运行按钮，运行程序。

六，示例代码

#define MAXN 20
#include <stdio.h>

void fun(int M[MAXN][MAXN], int n)
{
    int i, j, k = 0;
    for (i = 0; i < (n + 1) / 2; i++) {
        // 产生第i圈左边的数字（从上到下）
        for (j = i; j < n - i; j++) {
            k++;
            M[j][i] = k;
        }
        // 产生第i圈下边的数字（从左到右）
        for (j = i + 1; j < n - i; j++) {
            k++;
            M[n - 1 - i][j] = k;
        }
        // 产生第i圈右边的数字（从下到上）
        for (j = n - 2 - i; j >= i; j--) {
            k++;
            M[j][n - 1 - i] = k;
        }
        // 产生第i圈上边的数字（从右到左）
        for (j = n - 2 - i; j > i; j--) {
            k++;
            M[i][j] = k;
        }
    }
}

void main()
{
    int i, j, n;
    int M[MAXN][MAXN];
    while (1) {
        do {
            printf("\n  输入矩阵的阶(0-%d)(0:结束!)==>", MAXN - 1);
            scanf("%d", &n);
        } while (n < 0 || n >= MAXN);
        if (n == 0) return;
        fun(M, n);
        for (i = 0; i < n; i++) {
            for (j = 0; j < n; j++)
                printf("%4d", M[i][j]);
            printf("\n");
        }
    }
}

七，运行效果

1，实验要求的运行效果。

2，编写程序运行后的效果。