人工智能基础知识笔记五：相关分析

人工智能基础知识笔记五：相关分析

1、相关分析

相关分析是研究两个或两个以上的变量之间相关程度及大小的一种统计方法。

在数学上，研究两个或两个以上处于同等地位的事物之间相关程度的强弱，并用适当的统计指标表示出来的过程，称为相关分析。根据相关分析，可以从不同角度对事物的相关性进行分类。

1.1、相关分析的类型

1. 按照相关程度可以分成完全相关、不完全相关和不相关。一个变量的数量变化由另一个变量的数量变化所确定，称为完全相关,即函数关系;两个变量的数量变化各自独立，称为不相关介于完全相关与不相关之间的称不完全相关。
2. 按照相关的方向分为正相关和负相关。正相关指相关变量的数量变动方向一致，负相关指相关变量的数量变动方向相反。
3. 按照相关的形式分成线性相关和非线性相关。将相关变量值作为直角坐标系的坐标,变量的不同取值如果呈直线分布，称为线性相关;如果呈曲线分布，称为非线性相关。

1.2、线性相关

线性相关的两个变量之间的相关程度可以通过一个量化的相关系数r来表示。相关系数有以下几个特点。

1. r的数值范围是-1~+1。
2. r的绝对值表示变量之间的密切程度(即强度)。绝对值越接近1，表示两个变量之间关系越密切;越接近0，表示两个变量之间关系越不密切。
3. r的正负号表示变化方向。+”号表示变化方向一致，即正相关;“_”号表示变化方向相反，也就是负相关。
4. 相关系数的值仅仅是一个比值。它不是由相等单位度量而来的(即不等距)，也不是百分比，因此，不能直接进行算术运算。
5. 相关系数只能描述两个变量之间的变化方向及密切程度，并不能揭示两者之间的内在本质联系，即相关的两个变量不一定存在因果关系。

可以通过散点图来直观地观察随机变量之间的相关性。下面来看一下相关系数取不同值时对应的图形。

上图将具有相关关系的变量值作为直角坐标系中点的坐标，变量的不同取值对应不同的坐标点，绘制这些离散的点就构成散点图。可以看到在图(a)中，相关系数是-0.93，两个量之间存在较强的负相关，变量之间的变化基本符合直线关系，一个变量增加时，另一个变量倾于减少。在图(b)中，相关系数为 +0.92，两个变量之间存在较强的正相关，变量之间的变化基本符合直线关系，一个变量增加时，另一个变量也倾向于增加。

下面来看较弱的相关形式和非线性相关的图形。

上图显示了较弱的正相关和非线性相关的图形。可以看到在上图(a)中，相关系数是+0.23，两个变量之间存在较弱的正相关，变量有同向正向变化的趋势。上图(b)中，线性相关系数为0，可是变量之间却存在一种有意义的非线性相关关系。由此可见，相关系数是描述线性相的量，不能描述变量之间的非线性相关关系。

1.3、线性相关系数

1.3.1、皮尔森相关系数

皮尔森(Pearson)相关系数是用来度量两个连续型的随机正态变量之间的线性关系的一种随机变量特征量。连续型随机变量是指可以进行算术运算的一些量，如国民收人与居民储蓄存款、身高与体重、高中成绩与高考成绩等。皮尔森相关系数和随机变量的协方差关系比较密切，下面先来看一下什么是协方差。

协方差是反映两个随机变量相关程度的指标，下面是协方差的数学表示。

cov(x,)=E{x-E(x)][r-E(r)]}=E(xY)-E(X)E(Y)

上式中X、Y是随机变量,E表示随机变量的期望值。当随机变量相互独立时，由公式(13-1)可知，协方差cov为0;当随机变量相互不独立，即存在相关关系时，cov不为0;cov>0，表示两者正相关;cov<0，表示两者负相关。

对于样本数据，可以构建样本协方差如下：

协方差可以在一定程度上反映随机变量的相关性，但协方差受方差的影响较大，不同的相关变量的方差差异很大时，协方差数值很难建立不同组相关变量对的相关关系的对比。

为了更好地度量两个随机变量的相关程度，对协方差公式进行修正，可以在其基础上除以两个随机变量的标准差，这就是皮尔森相关系数，可以用以下公式表示。

上式中，X、Y是随机变量，Px是皮尔森相关系数,ax和。,是标准差,E是随机变量的期望值,皮尔森系数是一个介于-1~1的值，当两个变量的线性关系增强时，相关系数趋于1或-1;当一个变量增大，另一个变量也增大时，表明它们之间是正相关的，相关系数大于0;如果一个变量增大，另一个变量却减小，表明它们之间是负相关的，相关系数小于0;如果相关系数等于0,表明它们之间不存在线性相关关系。

皮尔森相关系数对于随机变量是对称的，即Px=pn;对于两组数据，皮尔森系数是一个具体的值;对于多组数据，要求出两两之间的相关系数，则相关系数实际上是一个矩阵。

皮尔森系数能够较好地描述两个变量的相关关系。当皮尔森系数为0时，坐标点完全离散化;当皮尔森系数为正时，散点图沿斜率为正的直线分布;当皮尔森系数为1时，散点图基本上呈现为条斜率为正的直线。

使用 Python 代码计算二维数组中行数据之间的皮尔森相关系数和列数据之间的皮尔森相关系数。

import numpy as np

tang =np.array([[9,7,6，2，5][3，7，1，5，3]，[8,9,2,3，2]])





row_coef = np.corrcoef(tang)

print("corrcoef between row')

print(row_coef)



col_coef = np.corrcoef(tang,rowvar=0)

print("corrcoef between column')

print(col_coef)

计算出具体的系数之后，可以根据https://blog.csdn.net/jimmyleeee/article/details/145858390介绍假设检验检验一下相关系数的显著性校验，来进一步判断计算的结果是否可信。

1.3.2、皮尔森相关系数

斯皮尔曼等级相关(Spearman's Correlation Coefcient for Ranked Data)主要用于解决名称数据和顺序数据相关的问题。当两个变量值以等级次序排列或以等级次序表示时，两个相应的总体并不定呈正态分布，样本容量也不一定大于30，这种情况下可以用斯皮尔曼等级相关来描述两个变之间的相关关系。

斯皮尔曼等级相关由英国统计学家斯皮尔曼根据积差相关的概念推导而来，用公式可以表示为：

式中n为等级个数，d为二列成对变量的等级差数。

从公式可以看出，斯皮尔曼等级相关简单而言，就是无论两个变量的数据如何变化符合什么样的分布，我们只关心每个数值在变量内的排列顺序。如果两个变量的对应值在各组内的排序顺位是相同或类似的，则这两个变量具有显著的相关性。严格来说，公式主要用于同一变量无相同等级时斯皮尔曼等级相关系数的计算;当同变量有相同等级时，也可用它进行近似计算。

斯皮尔曼等级相关系数显著性检验

在统计学上，经常需要根据样本推断总体的一些性质。一般的做法是根据样本数据提出某些关于总体的假设，再根据样本数据确定这些假设在统计学上是有意义的，这实际上就是假设检验。上皮尔森系数的显著性检验类似，根据斯皮尔曼系数推断数据相关性的显著性水平，也可以用1检验其检验统计量如下：

式中"表示斯皮尔曼相关系数，"表示样本数据个数。在实际使用时，可以按照以下步骤进行显著性检验。

(1)建立关于总体的两个假设，H:P=0，H:p≠0。

(2)设定一个显著性水平，比如 a=0.01。

(3)根据表格得到双边检验或单边检验的a分位点。

(4)根据样本数据，计算当前t值。

(5)如果t≥4，说明小概率事件发生，即假设H:p-0不合理，样本数据存在斯皮尔曼相关关系;反之，则不能说明样本数据之间存在斯皮尔曼相关关系。

计算斯皮尔曼等级相关系数的python示例代码如下：

import numpy as np

import scipy.stats as stats



x=[3.78,5.75,2.38,9.12,1.98,8.78,3.25,7.81,9.35,11.21]

y=[4.32,5.25,2.31,5.23,1.87,5.12,1.99,3.89,5.21，6.01]



correlation,pvalue =stats.spearmanr(x,y)



print('correlation',correlation)

print('pvalue',pvalue)

1.3.2、肯德尔系数

皮尔森相关、斯皮尔曼等级相关描述的是两个变量的相关程度，当表示多个(两个以上)处之间相关关系时，就要用到肯德尔系数。

肯德尔(Kandal)相关系数(即和谐系数)是用来描述多个(即两个以上)等级变量之间的一致性程度的量。通常为K个评分者评N个对象，或者也可以是同一个人先后K次评N个对象，通过肯德尔系数描述K个评分者对N个对象评价的一致性。肯德尔系数按照同一评价者有无相同等级评定，可以分成以下两种情况。

        1. 同一评价者无相同等级评定时

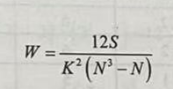
式中，N表示被评的对象数，K表示评分者人数或评分所依据的标准数，S表示每个被评对象所评等级之和R与所有这些和的平均数的离差平方和。

其中S又可以表示为：

式中R是K个评委对第i个对象所评等级之和，表示所有等级之和的平均数。

当评分者意见完全一致时，S取得最大值，可见相关系数是实际求得的S与其最大可能取值的比值，所以O≤W≤1。

        2. 同一评价者有相同等级评定时

式中，K、N、S的意义同公式(13-6);其中，可以表示为：

这里，m为第i个评价者评定结果中有重复等级的个数;nij为第个评价者的评定结果中第i个重复等级的次数;对评定结果无相同等级的评价者，Ti=0，因此只需对评定结果有相同等级的评价者计算Ti。

1.4、质量相关性分析

1.4.1 二列相关

当两个变量都是正态连续变量，其中一个变量被人为地划分成二分变量(如按一定标准将属于正泰连续交量的考试分数划分为及格与不及格、录取与未录取，把某一体育项目测验结果划分为通过与未通过、达标与未达标，把健康状况划分为好与差等)，这个正态连续变量与二分变量之间的朕关系称为二列相关。二列相关可以用如下数学公式表示。

式中p表示二分变量中某一类别频率的比率,q表示二分变量中另一类别频率的比率，表示与二分变量中p类别相对应的连续变量的平均数，表示与二分变量中q类别相对应的连续变量平均数,σ表示连续变量的标准差，表示正态曲线中与累积概率p相对应的概率密度函数值。根据二列相关定义，二列相关的使用条件如下：

(1)两个变量都是连续变量，且总体呈正态分布或接近正态分布，至少是单峰对称分布。

(2)两个变量之间是线性关系。

(3)二分变量是人为划分的，其分界点应尽量靠近中值。

(4)样本容量应大于80。

1.4.2 点二列相关

质量分析中用来描述事物总体性质的离散变量，如果其本质上就具有离散性质，而不是人为地将连续变量划分成离散变量，这时候的相关关系称为点二列相关。

有两个随机变量，其中一个是正态连续变量，另一个是真正的二分名义变量(例如，男与女已婚和未婚、色盲与非色盲、生与死等)，这两个变量之间的相关关系称为点二列相关。点二列相关关系可以用以下公式表示：

p表示二分变量中某一类别频率的比率,q表示二分变量中另一类别频率的比率，表示与分变量中p类别相对应的连续变量的平均数，表示与二分变量中q类别相对应的连续变量平均数，σ表示连续变量的标准差。

Python示例代码如下：

import scipy.stats as stats

x=[1,0,0,0,0,0,0,1,1,1,1,0,1,1,1,1,1,0,0,0]

y=[85,81,75,61,71,75,78,86,89,91,79,81,91,93,95,87,91,76,75,72]



coef,pvalue=stats.pointbiserialr(x，y)

print('点二列相关系数',coef)

print('P值',pvalue)

1.5、品质相关性分析

1.5.1、列联相关系数

列联相关系数（Contingency Coefficient）是一种用于衡量两个分类变量之间关联程度的统计量，特别适用于列联表（交叉表）数据。它的核心思想是看两个变量的分类是否有关联（比如：性别是否与喜欢的颜色有关）。

两个都是分类变量（如性别-男/女，教育程度-高中/大学等）。基于卡方检验（χ²）的统计量，公式为：

χ2：卡方值（反映实际频数与期望频数的差异）。

n：总样本量。

结果范围：0 到 1 之间（但达不到1）。0表示完全无关联；接近1：关联性强（但实际最大值取决于分类数，例如2×2表时最大为0.707）。

列联相关系数是描述分类变量关联性的指标，值越大关联越强，但需注意其局限性。实际分析中，Cramer's V可能更通用。

1.5.2、φ 相关

当两个变量都是二分变量，无论是真正的二分变量还是人为的二分变量，这两个变量之间的相关系数称为φ相关系数(Phi-Coecient)。如性别与体育成绩是否达标的相关关系，城镇户口与农村户口和创新能力强弱之间的相关关系等。

两个变量都是二分类的，比如：性别（男/女） vs. 是否吸烟（是/否）；考试（通过/不通过） vs. 补习（参加/未参加）等。

通过卡方值（χ²）计算得出：

χ2：卡方值（反映实际频数与期望频数的差异）。

n：总样本量。

结果范围：0：两变量完全无关。+1：完全正相关（比如“男性全吸烟，女性全不吸烟”）。-1：完全负相关（比如“男性全不吸烟，女性全吸烟”）。

总之，φ相关系数是二分类变量的“关联强度计”，-1到1之间，0代表无关，±1代表完全关联。

1.6、偏相关和复相关

1.6.1、偏相关

偏相关（Partial Correlation）是一种用于衡量两个变量之间的“纯关系”的统计方法，即在排除其他变量影响后，看这两个变量到底有多相关。

有时候两个变量看似相关，但实际上是因为它们都受第三个变量的影响。比如：冰淇淋销量（X）和溺水事件（Y）在夏季都增加，看似相关，但其实是因为气温（Z）升高。用偏相关可以排除气温（Z）的影响，直接看X和Y的关系。

例如：控制Z变量计算X和Y的相关关系：

rXY​：X和Y的普通相关系数。

rXZ、rYZ​：X和Z、Y和Z的相关系数

结果: 范围是-1到1，和普通相关系数一样。0：排除Z后，X和Y无线性关系。正值/负值：排除Z后，X和Y仍存在正向/负向关联。

偏相关是“排除干扰后”的纯净相关系数，帮你揪出变量之间真实的关联。

1.6.2、复相关

复相关是衡量一个变量（比如考试成绩）和多个其他变量（比如学习时间、智商、睡眠质量）整体关联程度的指标，范围在0到1之间，越接近1表示整体关联性越强。

普通相关（如Pearson）只能分析两个变量的关系，而复相关可以回答：“如果把学习时间、智商、睡眠一起考虑，它们对考试成绩的整体解释力有多强？”常用于多元回归分析中，评估模型的预测效果。

复相关系数（R）是因变量（Y）与多个自变量（X₁, X₂…）的联合预测值之间的相关系数。计算公式：

式中，ry1表示变量y和x1之间的相关系数，ry2表示变量y和x2在排除了x1影响时的偏相关关系系数。

当有3个自变量x1、x2、x3时，复相关系数可以按照下面的公式进行计算。

随着变量的增多，可以以此类推。

对于复相关系数，有以下几个性质：

1. 反映几个要素与某一个要素之间的复相关程度。复相关系数介于 0~1。
2. 复相关系数越大，则表明要素(变量)之间的相关程度越密切。复相关系数为1，表示完全相关;复相关系数为0，表示完全无关。
3. 复相关系数必大于或至少等于单相关系数的绝对值。
4. 复相关系数必大于或至少等于同一系列数据所求得的偏相关系数的绝对值，即      R1，23>|r123|。

注意事项：

1. 复相关只反映线性关系，如果实际关系是非线性的（如U型曲线），可能需要其他方法。
2. 高R值不一定因果：即使多个X联合与Y强相关，仍需验证是否存在因果关系。
3. 变量选择很重要：加入无关变量可能虚高R值，建议结合理论筛选变量。

总之，复相关是“多对一”的关联强度指标，帮你回答：“这些因素加起来，到底对结果有多大影响？” 它是多元分析中的重要工具，但需谨慎解释结果！