【动态规划】路径问题

个人主页 ： zxctscl
如有转载请先通知

前言

在上一篇有关动态规划的博客中，谈到做这类题目的步骤，有需要的可以点这个链接: 【动态规划】斐波那契额数列模型。继续分享这个模型类型的题目。

1. 62.不同路径

1.1 分析

题目要求不能回退，就是不能往左和往上。
如果有3*2个表格：那么到达就有三种情况：

1. 状态表示：以i位置为结尾，就是走到i位置有多少种方式。
2. 状态转移方程：根据最近的一步划分有两种情况：到达[i][j]位置，（1）从上面一个[i-1][j]下来一步;（2）从左边[i][j-1]过来一步
   状态转移方程：dp[i][j]=dp[i-1][j]+dp[i]dp[j-1]。
3. 初始化，下面这些位置可能会存在越界
   所以可以先初始化这些可能初始化的位置。还可以在外面先虚拟一些空间，让下面这些就不会越界：
   
   这些虚拟空间的值要保证后面填表顺序是正确的，要想填表正确，虚拟空间值设置就是：
   
4. 填表顺序：从左往右，从上往下
5. 返回值：看题目要求直接返回dp[m][n]就行

1.2 代码

class Solution {
public:
    int uniquePaths(int m, int n) {

        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        dp[0][1] = 1;

        for (int i = 1; i <= m; i++)
            for (int j = 1; j <= n; j++)
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        return dp[m][n];

    }
};

2. 63.不同路径 II

2.1 分析

题目与上面的类型是相同的，就是多了一个障碍物。

1. 状态表示：以i位置为结尾，就是走到i位置有多少种方式。
2. 状态转移方程：根据最近的一步划分有三种情况：到达[i][j]位置，（1）从上面一个[i-1][j]下来一步;（2）从左边[i][j-1]过来一步；（3）这个位置时障碍物那么就是0，就多加一个判断障碍物就可以了。
   状态转移方程：dp[i][j]=dp[i-1][j]+dp[i]dp[j-1]。
3. 初始化，下面这些位置可能会存在越界，所以就多开一组虚拟空间，得注意下标的映射。如果是障碍物位置就得对应减一。
   
4. 填表顺序：从左往右，从上往下
5. 返回值：看题目要求直接返回dp[m][n]就行

2.2 代码

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m=obstacleGrid.size(),n=obstacleGrid[0].size();

       vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        dp[0][1] = 1;

        for (int i = 1; i <= m; i++)
            for (int j = 1; j <= n; j++)
             if(obstacleGrid[i-1][j-1]==0)
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        return dp[m][n];
    }
};

3. LCR166. 珠宝的最高价值

3.1 分析

1. 状态表示
   以[i][j]位置为结尾，表示到达[i][j]位置时，此时的最大价值。

2. 状态转移方程
   要在[i][j]位置时候得到最大价值，要么从它上面的一个下来，要么从它左边一个过来，但是选择的是价值更大的那一个,再加上它本身那一个所对应的价值
   dp[i][j]=max(dp[i-1][j],dp[i][j-1])+frame[i][j]

3. 初始化
   这里也是要涉及到可能会越界问题，就直接多开一行和一列，为了不影响价值计算的结果就全部都初始化为0。这里得注意下标的映射，此时在dp[i][j]位置就对应frame[i-1][j-1]，写代码时候得注意。
   

4. 填表顺序
   从上往下，从左往右

5. 返回值
   直接返回dp[m][n]就行
   

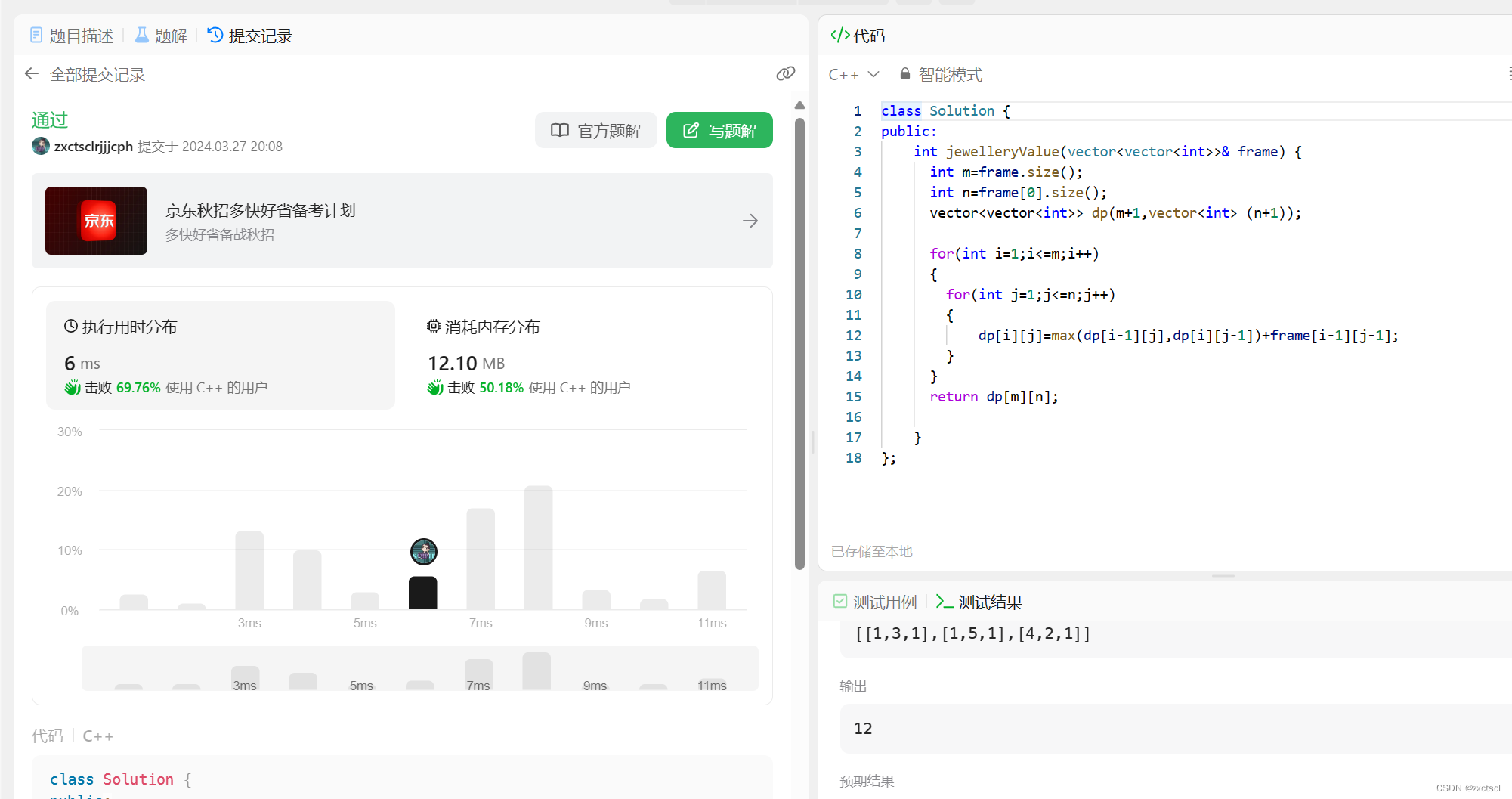
3.2 代码

class Solution {
public:
    int jewelleryValue(vector<vector<int>>& frame) {
      int m=frame.size();
      int n=frame[0].size();
      vector<vector<int>> dp(m+1,vector<int> (n+1));
    
      for(int i=1;i<=m;i++)
      {
        for(int j=1;j<=n;j++)
        {
            dp[i][j]=max(dp[i-1][j],dp[i][j-1])+frame[i-1][j-1];
        }
      }
      return dp[m][n];

    }
};

4. 931.下降路径最小和

4.1 分析

1. 状态表示
   同样是以[i][j]位置结尾，来找下降路径的最小和。

2. 状态转移方程

想要到达[i][j]位置有三种方式[i-1][j-1]和[i-1][j]还有[i-1][j+1]，

而题目要求的是最小和，那么就取这三个位置的最小值和，再加上这个位置本身的值

3. 初始化
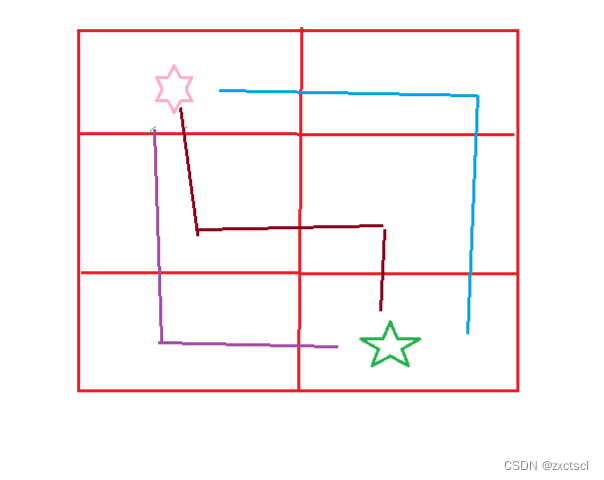
   像绿色星号标注的位置可能会存在越界的问题，所以就多开两列和一行。但是想让填表时候第一行位置所在的值不变，那么新开空间的第一行就初始化为0：
   
   但如果也把左边开的这一列初始化为0，那么红色格子这格的最小值和可能就会用到这个0，所以这里不能写0，为了不改变选择的结果，就把这些初始化为INT_MAX

4. 填表顺序
   从上往下

5. 返回值
   返回最后一行最小的值
   

4.2 代码

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
     int n=matrix.size();
     vector<vector<int>> dp(n+1,vector<int> (n+2,INT_MAX));
     for(int j=0;j<n+2;j++)dp[0][j]=0;

     for(int i=1;i<=n;i++)
     {
        for(int j=1;j<=n;j++)
        {
            dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j],dp[i-1][j+1]))+matrix[i-1][j-1];
        }
     }
     int ret=INT_MAX;
     for(int j=1;j<=n;j++)
       ret=min(ret,dp[n][j]);

    return ret;
    }
};

5. 64.最小路径和

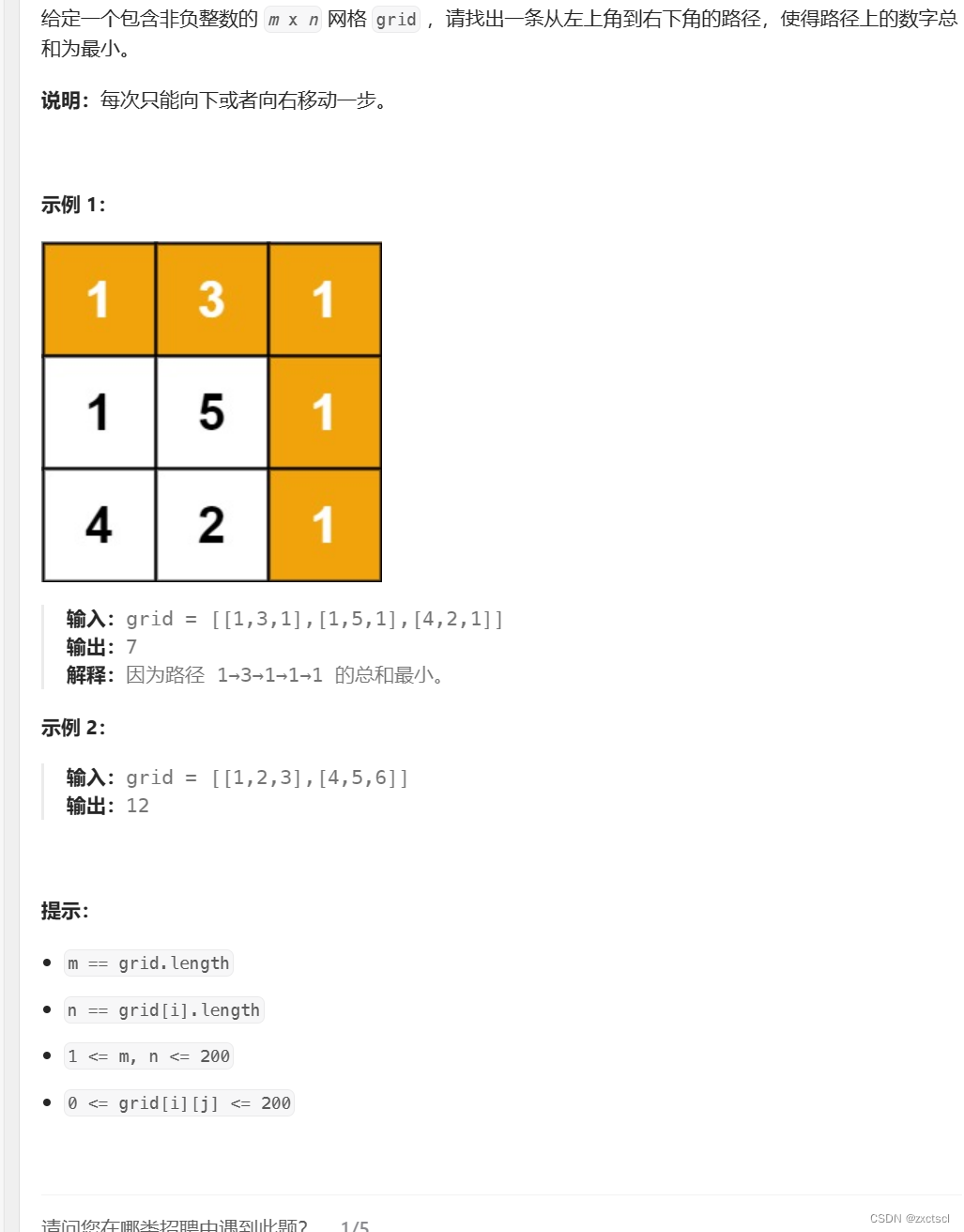
5.1 分析

1. 状态表示
   以[i][j]为结尾，找最小和。
   dp[i][j]表示到达[i][j]位置时，最小路径和。

2. 状态转移方程
   根据最近的一步划分问题。
   到到达[i][j]位置有两种方式，一种从上面，一种从左边
   
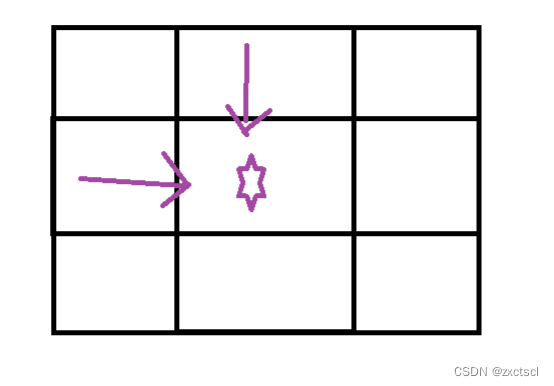
   一种是以最小的路径到上面，然后加上当前位置的值；
   另一种是最小的路径到左边，然后加上当前位置的值。
   
   所以到达的dp[i][j]最小值就是，两种中取最下的那一个
   

3. 初始化
   这里可能会存在越界访问的情况，所以多开一行和一列。但要注意里面填的值，要保证在后面计算的结果是正确的。
   第一行第一列为了值不被改变，就得在新开空间的上面一格和左边一格的值为0，其他的为了不影响后面取最小值和的计算，都初始化为INT_MAX
   

4. 填表顺序
   从上往下，从左往右

5. 返回值
   要求每个位置的最小值，就直接返回dp[m][n]
   

5.2 代码

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
     
     int m=grid.size(),n=grid[0].size();
     vector<vector<int>> dp(m+1,vector<int> (n+1,INT_MAX));
     dp[0][1]=dp[1][0]=0;

     for(int i=1;i<=m;i++)
     {
        for(int j=1;j<=n;j++)
        {
            dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
        }
     }
     return dp[m][n];
    }
};

6. 174. 地下城游戏

6.1 分析

1. 状态表示
   如果以某一个位置为结尾，那么dp[i][j]表示：从起点出发，到达[i][j]位置的时候，所需的最低初始健康点数。
   填表顺序是从上往下，从左往右，要考虑到达这个位置时的最低健康点数，它前面一个位置，可能是上方，也可能是左方。想要继续往右下角走，这个位置的最低健康点数，又受到下一个位置的影响，不能更新这个状态，所以用这个状态表示就不合适。
   
   

以某个位置为起点，此时的dp[i][j]表示：从[i][j]位置出发，到达终点，所需的最低初始健康点数。

2. 状态表示方程

从[i][j]位置出发，要到达终点，就得往右或者往下出发，直到到达终点。

就分两种情况：
（1）往右走：得考虑假设最初的健康指数是x，那么要想到达右边，x加上原表中d[i][j]的值就得大于d[i][j+1]，所以此时所需要的最低健康指数就是dp[i][j+1]-d[i][j]。
（2）往下走：同理，要想到达下边x加原表[i][j]的值就得大于dp[i+1][j]，所以此时所需要的最低健康指数就是dp[i+1][j]-d[i][j]。

要得到的是最低健康点数，就取这两种情况的最小值：dp[i][j]=min(dp[i][j+1],dp[i+1][j])-d[i][j]。
但是如果dp[i][j]很大，减出来小于或者等于0，就不符合要求，此时就和1比较，取最大，也就是dp[i][j]=max(1,dp[i][j])。

3. 初始化
   保证填表时候不越界，要依靠的是右边和下边，就在最右边加一列，最下边加一行。
   当救完公主后的dp[i][j]要的是是健康点数的最大值，为了不影响，它的右边和下边都是1。而其它位置求的是最小健康点数，就用正无穷。
   

4. 填表顺序
   从下往上填每一行，每一行从右往左。

5. 返回值
   返回dp[0][0]就行。

6.2 代码

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int m=dungeon.size(),n=dungeon[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));

        dp[m][n-1]=dp[m-1][n]=1;

        for(int i=m-1;i>=0;i--)
        {
            for(int j=n-1;j>=0;j--)
            {
                dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j];
                dp[i][j]=max(1,dp[i][j]);
            }
        }
        return dp[0][0];      
    }    
};

有问题请指出，大家一起进步！！！