理解线性动力学中的模态叠加法

线性动力学中的模态叠加方法

模态叠加法是线性动力学中一种有价值的工具，可以有效地确定频域或时域中的系统响应。对于某些类型的线性动力学分析，有必要使用此方法，因此了解该过程对于获得准确的结果至关重要。在本博客中，我们将简要介绍各种类型的线性动力学分析，并提供有价值的见解，以帮助用户更好地理解并将这些方法应用于他们的工程问题。那么，让我们立即开始吧！

理解模态分析

 

图 1：固有频率结果示例

模态分析是模态叠加法的基石，为了解结构如何振动提供了重要见解。该技术有助于提取有关设计的关键信息：

• 固有频率
• 模态振型
• 模式参与因素
• 预应力效应

工程师可以利用模态分析的结果更深入地了解结构在不同动态载荷条件下的行为方式。

什么是模态叠加法？

模态叠加法 (MSUP) 是一种快速有效的解决动态问题的方法。它涉及以线性方式组合多个模态。模态叠加是一种强大的技术，它使用从模态分析中获得的固有频率和模态形状来有效捕捉结构在各种激励下的动态行为。 

使用模态叠加法解决动力学问题需要进行模态分析，包括：

• 谐波
• 随机振动
• 反应谱
• 瞬态动力学

 

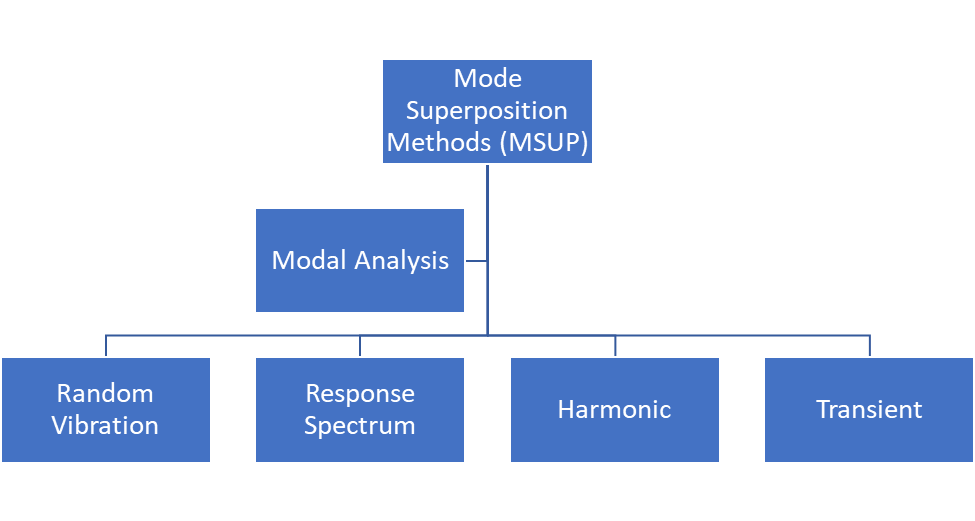
随机振动分析

随机振动分析用于确定组件如何响应随机振动。输出是功率谱下的响应概率分布，表示激励的概率分布。示例包括：

• 受风致振动的桥梁
• 生产线上或车辆内的零件
• 在道路上行驶的车辆
• 航天器发射期间

反应谱分析

响应谱分析主要用于代替时间历史分析，以确定结构在表示响应的谱下对随机或时间相关的载荷条件的响应。示例包括：

• 地震期间经历地震活动的建筑物。
• 暴风雨期间桥梁面临强风。
• 恶劣天气条件下的海上平台遭遇海浪载荷。
• 火箭发动机振动。
• 冲击测试。

谐波分析

谐波分析用于确定结构对稳定谐波载荷（正弦变化）的响应，从而为结构如何响应提供重要见解。示例包括：

• 受到旋转不平衡力的机械系统
• 高层建筑受风致谐波荷载的影响
• 正弦扫频
• 频率扫描

瞬态分析

瞬态分析可用于计算结构对时变载荷的响应。

• 对突然冲击或碰撞的结构响应
• 跌落测试
• 铁路影响
• 冲击测试