什么是有限元力学?分而治之,将复杂问题转化为可计算的数学模型
有限元力学是应用有限元方法(Finite Element Method, FEM)解决力学问题的学科,属于计算力学的重要分支。它通过将复杂的连续体结构离散化为有限个简单单元的组合,结合数学和物理原理,近似求解力学行为(如应力、应变、变形等),广泛应用于工程设计和科学研究。
核心概念
-
离散化
将复杂的几何结构或连续域划分为许多小的、简单的单元(如三角形、四边形、六面体等),这些单元通过节点相互连接,形成网格(mesh)。 -
单元与节点
每个单元内的物理行为(如应力、温度分布)通过数学插值函数(形函数)近似描述,节点处的未知量(如位移、温度)作为求解的核心变量。 -
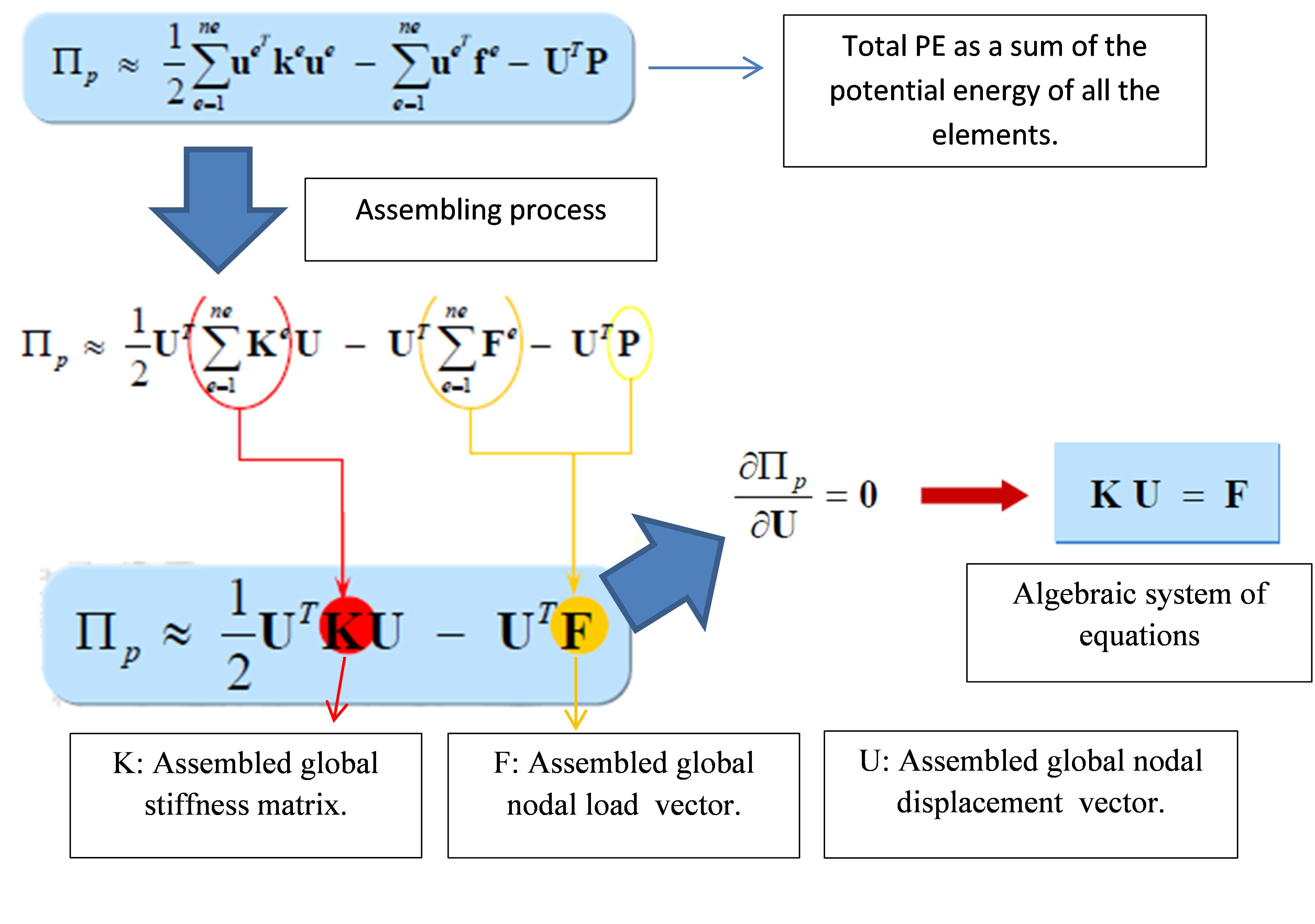
全局方程组
通过单元分析(建立单元刚度矩阵、载荷向量等)和整体组装,形成一个大型线性方程组,求解后得到节点处的物理量(如位移),再通过插值得到整个区域的解。
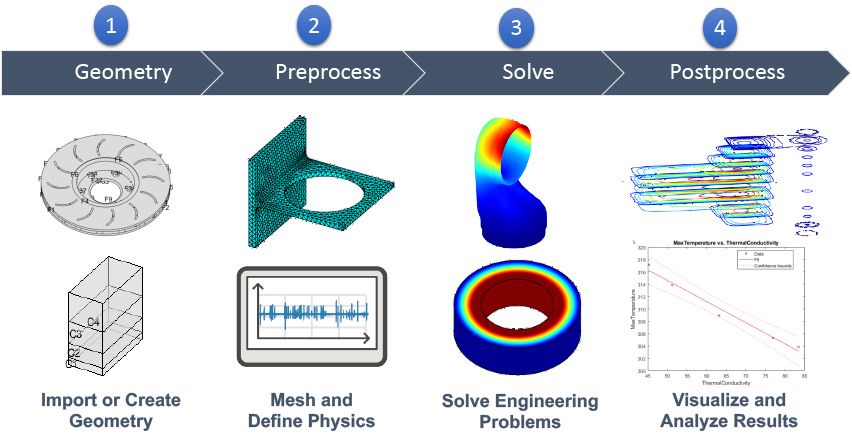
基本步骤
-
前处理
• 几何建模与网格划分:将问题域离散为有限元网格。
• 材料属性与边界条件:定义材料行为(如弹性模量)、载荷(如力、温度)和约束(如固定支撑)。 -
单元分析
• 对每个单元建立局部方程(如平衡方程),基于物理定律(如胡克定律、能量守恒)推导单元刚度矩阵和载荷向量。 -
整体组装
• 将单元方程组合为全局方程组,体现所有节点间的相互作用。 -
求解方程组
• 通过数值方法(如高斯消元法、迭代法)求解节点未知量(如位移)。 -
后处理
• 可视化结果(如应力云图、变形动画),评估安全性或优化设计。
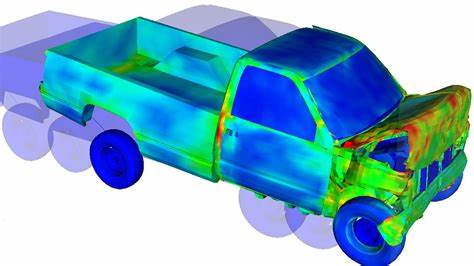
主要应用领域
• 结构力学:分析建筑物、桥梁、飞机机翼的应力与变形。
• 热力学:模拟散热器、电子元件的温度分布。
• 流体力学:计算流体在管道或机翼表面的流动特性。
• 电磁学:优化电机、天线的电磁场分布。
• 生物医学:模拟骨骼受力、心脏血流等。
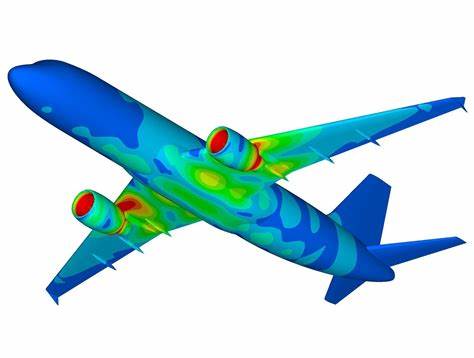
优势与特点
• 适应复杂几何:可处理不规则形状和非均匀材料。
• 灵活性与通用性:适用于多种物理场问题(多物理场耦合)。
• 高精度:通过细化网格或高阶单元提高计算精度。
• 工程实用性强:商业软件(如ANSYS、ABAQUS、COMSOL)已广泛集成FEM,支持工程设计与优化。
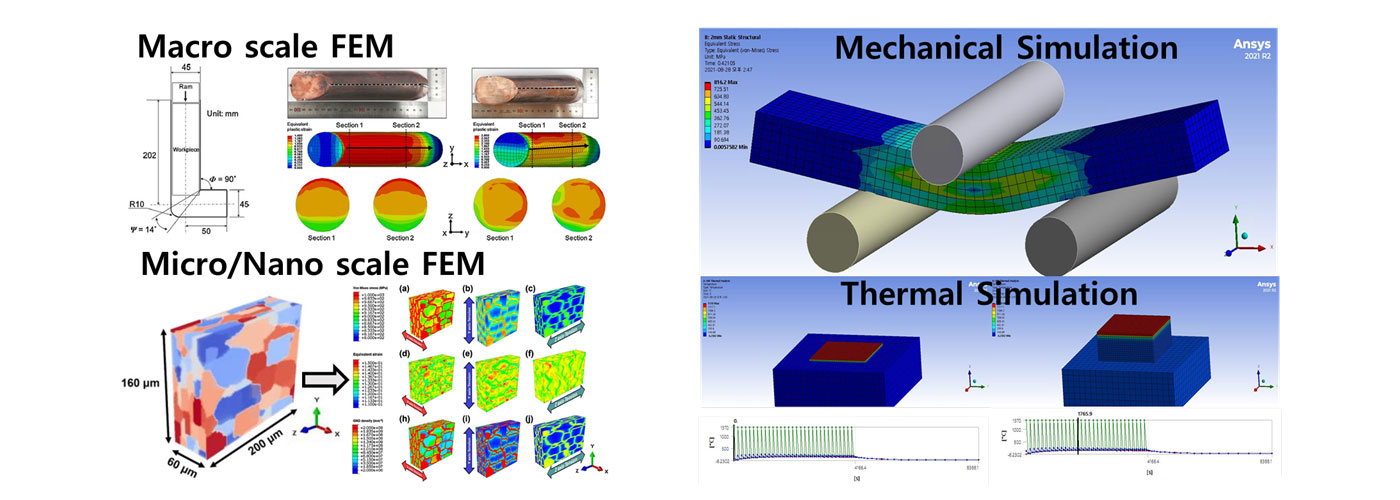
对比其他数值方法
• 有限差分法:适合规则网格和简单几何,但难以处理复杂边界。
• 边界元法:仅需离散边界,但限于线性问题。
• 有限体积法:常用于流体力学,强调守恒性。
简单案例
例如,在分析一座桥梁的受力时,FEM会将其离散为多个梁单元或壳单元,计算每个节点在载荷下的位移和应力,最终预测桥梁是否会发生断裂或过度变形。
总结来说,有限元方法通过“分而治之”的策略,将复杂问题转化为可计算的数学模型,成为现代工程分析和科学研究的基石之一。
