NRBO-Transformer牛顿-拉夫逊算法优化编码器多变量时间序列预测（Matlab实现）

NRBO-Transformer牛顿-拉夫逊算法优化编码器多变量时间序列预测（Matlab实现）

预测效果

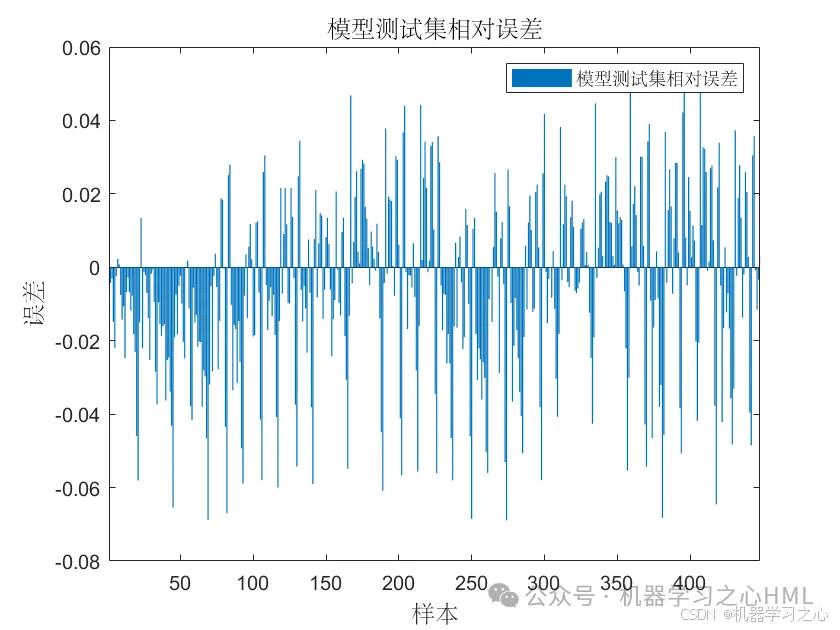
基本介绍

1.Matlab实现NRBO-Transforme牛顿-拉夫逊算法优化编码器多变量时间序列预测，运行环境Matlab2023b及以上；

牛顿-拉夫逊优化算法算法（Newton-Raphson-based optimizer，NRBO）是一种全新的元启发式优化方法，其灵感来源主要基于两个关键原理：Newton-Raphson搜索规则(NRSR)和陷阱避免算子(TAO)。NRSR使用Newton-Raphson方法来提高NRBO的探索能力，并提高收敛速度以达到改进的搜索空间位置。TAO有助于NRBO避免局部最优陷阱。NRBO具有进化能力强、搜索速度快、寻优能力强的特点。这一成果由Sowmya等人于2024年2月发表在中科院2区顶级SCI期刊《Engineering Applications of Artificial Intelligence》上。

代码中文注释清晰，质量极高，赠送测试数据集，可以直接运行源程序。替换你的数据即可用 适合新手小白

2.excel数据，方便替换，可在下载区获取数据和程序内容。

3.优化参数为注意力机制头数、学习率、正则化系数，图很多，包括预测效果图、误差分析图、决定系数图。

4.data为数据集，输入多个特征，输出单个变量，考虑历史特征的影响，多变量时间序列预测，main.m为主程序，运行即可,所有文件放在一个文件夹，运行环境为Matlab2023b及以上。

5.代码特点：参数化编程、参数可方便更改、代码编程思路清晰、注释明细。可在下载区获取数据和程序内容。

6.命令窗口输出R2、MSE、RMSE、MAE、MAPE、MBE等多指标评价；

注：程序和数据放在一个文件夹

程序设计

• 完整源码和数据获取方式私信回复NRBO-Transformer牛顿-拉夫逊算法优化编码器多变量时间序列预测（Matlab实现）。

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

%%  导入数据
result = xlsread('数据集.xlsx');

%%  数据分析
num_samples = length(result);  % 样本个数
kim = 2;                       % 延时步长（前面多行历史数据作为自变量）
zim =  1;                      % 跨zim个时间点进行预测
nim = size(result, 2) - 1;     % 原始数据的特征是数目

%%  划分数据集
for i = 1: num_samples - kim - zim + 1
    res(i, :) = [reshape(result(i: i + kim - 1 + zim, 1: end - 1)', 1, ...
        (kim + zim) * nim), result(i + kim + zim - 1, end)];
end

%%  数据集分析
outdim = 1;                                  % 最后一列为输出
num_size = 0.7;                              % 训练集占数据集比例
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim;                  % 输入特征长度

%%  划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);

P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, -1, 1);%将训练集和测试集的数据调整到0到1之间
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, -1, 1);% 对测试集数据做归一化
t_test = mapminmax('apply', T_test, ps_output);

%%  数据平铺
%   将数据平铺成1维数据只是一种处理方式
%   也可以平铺成2维数据，以及3维数据，需要修改对应模型结构
%   但是应该始终和输入层数据结构保持一致
p_train =  double(reshape(p_train, f_, 1, 1, M));
p_test  =  double(reshape(p_test , f_, 1, 1, N));
t_train =  double(t_train)';
t_test  =  double(t_test )';

%%  数据格式转换
for i = 1 : M
    Lp_train{i, 1} = p_train(:, :, 1, i);
end

for i = 1 : N
    Lp_test{i, 1}  = p_test( :, :, 1, i);
end

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/128577926?spm=1001.2014.3001.5501
[2] https://blog.csdn.net/kjm13182345320/article/details/128573597?spm=1001.2014.3001.5501