当前位置：首页 > news >正文

Leetcode 55

news 2025/11/17 13:50:32

1 题目

797. 所有可能的路径

给你一个有 n 个节点的 有向无环图（DAG），请你找出从节点 0 到节点 n-1 的所有路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

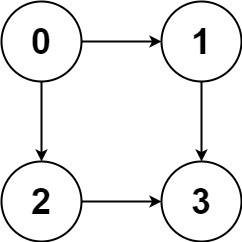
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

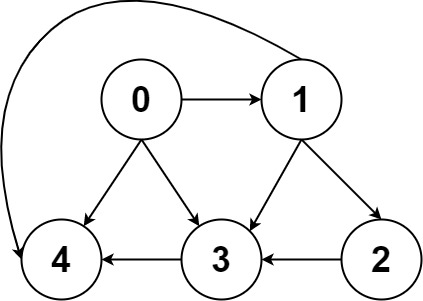
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

提示：

n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i（即不存在自环）
graph[i] 中的所有元素 互不相同
保证输入为 有向无环图（DAG）

2 代码实现

1. LeetCode 核心代码模式（只需要实现 Solution 类）

#include <vector>
using namespace std;class Solution {
private:vector<vector<int>> result;  // 存储所有路径vector<int> path;            // 存储当前路径// 深度优先搜索函数void dfs(int current, const vector<vector<int>>& graph, int target) {path.push_back(current);  // 当前节点加入路径// 如果到达终点，记录路径if (current == target) {result.push_back(path);} else {// 遍历所有可到达的下一个节点，递归搜索for (int next : graph[current]) {dfs(next, graph, target);}}path.pop_back();  // 回溯：移除当前节点，尝试其他路径}public:vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {int target = graph.size() - 1;  // 终点是最后一个节点（n-1）dfs(0, graph, target);          // 从起点0开始搜索return result;}
};

2. ACM 模式（完整可运行代码，包含输入输出）

#include <iostream>
#include <vector>
using namespace std;class Solution {
private:vector<vector<int>> result;vector<int> path;void dfs(int current, const vector<vector<int>>& graph, int target) {path.push_back(current);if (current == target) {result.push_back(path);} else {for (int next : graph[current]) {dfs(next, graph, target);}}path.pop_back();}public:vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {int target = graph.size() - 1;dfs(0, graph, target);return result;}
};int main() {// 读取输入（图的邻接表）int n;cin >> n;  // 节点数量vector<vector<int>> graph(n);for (int i = 0; i < n; ++i) {int m;cin >> m;  // 第i个节点的邻接节点数量graph[i].resize(m);for (int j = 0; j < m; ++j) {cin >> graph[i][j];  // 邻接节点的值}}// 计算并输出结果Solution solution;vector<vector<int>> paths = solution.allPathsSourceTarget(graph);// 按照题目要求的格式输出所有路径cout << "[";for (size_t i = 0; i < paths.size(); ++i) {cout << "[";for (size_t j = 0; j < paths[i].size(); ++j) {cout << paths[i][j];if (j != paths[i].size() - 1) {cout << ",";}}cout << "]";if (i != paths.size() - 1) {cout << ",";}}cout << "]" << endl;return 0;
}

输入输出说明（ACM 模式）

输入格式：第一行输入节点数量 n接下来 n 行，每行先输入一个整数 m（表示当前节点的邻接节点数量），然后输入 m 个整数（邻接节点的值）
示例输入（对应示例 1）：
```
4
2 1 2
1 3
1 3
0
```
输出格式：按照 LeetCode 要求的格式输出所有路径（如 [[0,1,3],[0,2,3]]）

可以直接将 ACM 模式代码复制到本地编译器（如 Dev-C++、VS Code）中运行，输入示例数据即可看到结果。

详解

一、彻底理解问题：什么是 “图” 和 “路径”？

1. 图的表示方式

题目里的 graph 是一个二维数组，叫做 “邻接表”，专门用来表示图。比如 graph = [[1,2],[3],[3],[]] ：

索引 i 表示 “当前节点”（地点）
graph[i] 里的元素表示 “从节点 i 出发，能直接到达的节点”（从当前地点出发的单向路）

具体来说：

graph[0] = [1,2] → 节点 0 有两条路：0→1，0→2
graph[1] = [3] → 节点 1 有一条路：1→3
graph[2] = [3] → 节点 2 有一条路：2→3
graph[3] = [] → 节点 3 没有路（终点）

2. 什么是 “路径”？

路径就是 “从起点到终点，依次经过的节点序列”。比如上面的例子，起点是 0，终点是 3（因为 n=4，n-1=3），所以路径就是：

0→1→3（先从 0 到 1，再从 1 到 3）
0→2→3（先从 0 到 2，再从 2 到 3）

二、解题思路：如何找到所有路径？

因为要找 “所有可能的路径”，我们需要一种 “不遗漏” 的搜索方法。可以想象成 “走迷宫”：从起点出发，尝试所有岔路，走到终点就记录路线，走不通就回头换一条路。这就是深度优先搜索（DFS）。

搜索步骤（以示例 1 为例）：

从起点 0 出发，当前路径是 [0]
0 有两个岔路：1 和 2，先试试 1：
- 走到 1，路径变成 [0,1]
- 1 只有一个岔路 3，走到 3，路径变成 [0,1,3]
- 3 是终点，记录这条路径
- 回头（回溯）到 1，再回头到 0，路径变回 [0]
再试试 0 的另一个岔路 2：
- 走到 2，路径变成 [0,2]
- 2 只有一个岔路 3，走到 3，路径变成 [0,2,3]
- 3 是终点，记录这条路径
- 回溯到 2，再回溯到 0，所有路都试完了

三、代码逐行解析（超详细版）

我们用 C++ 实现，核心是用 DFS 递归 + 回溯。

1. 准备工作：定义变量

#include <iostream>
#include <vector>  // 用vector存储路径和结果
using namespace std;class Solution {
public:// 存储所有找到的路径（最终要返回的答案）vector<vector<int>> result;// 存储当前正在走的路径（临时变量，随时更新）vector<int> path;

2. DFS 函数：递归探索路径

    // 函数作用：从当前节点current出发，探索所有可能的路径// 参数：// current：当前所在的节点（比如0、1、2等）// graph：整个图的邻接表（地图）// target：终点（n-1，比如示例1中的3）void dfs(int current, const vector<vector<int>>& graph, int target) {// 第一步：把当前节点加入“当前路径”中path.push_back(current);  // 比如当前在0，path就变成[0]// 第二步：判断是否到达终点if (current == target) {// 如果到终点了，就把当前路径存入resultresult.push_back(path);  // 比如[0,1,3]存入result} else {// 没到终点，就遍历当前节点的所有“岔路”（邻居节点）for (int next : graph[current]) {  // graph[current]是当前节点能去的所有节点dfs(next, graph, target);  // 递归：去下一个节点探索}}// 第三步：回溯（关键！）path.pop_back();  // 把当前节点从路径中移除，回到上一步}

3. 主函数：启动搜索

    // 函数作用：入口函数，返回所有从0到n-1的路径vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {int n = graph.size();  // n是节点总数（比如示例1中graph有4个元素，n=4）int target = n - 1;    // 终点是最后一个节点（n-1）// 从起点0开始搜索dfs(0, graph, target);return result;  // 返回所有找到的路径}
};

4. 测试代码

int main() {// 测试示例1：graph = [[1,2],[3],[3],[]]vector<vector<int>> graph1 = {{1,2}, {3}, {3}, {}};Solution solution;vector<vector<int>> result1 = solution.allPathsSourceTarget(graph1);// 打印结果cout << "示例1的所有路径：" << endl;for (const auto& p : result1) {  // 遍历每条路径for (int node : p) {         // 遍历路径中的每个节点cout << node << " ";}cout << endl;  // 每条路径换行}// 输出应该是：// 0 1 3 // 0 2 3 return 0;
}