当前位置：首页 > news >正文

二叉树的前序遍历

news 2025/11/17 9:10:29

一、题目内容

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：

输入：root = [1,null,2,3]

输出：[1,2,3]

解释：

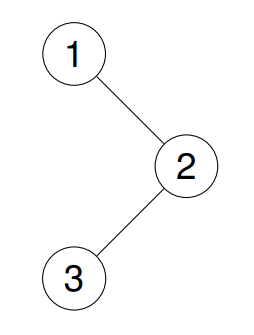
示例 2：

输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]

输出：[1,2,4,5,6,7,3,8,9]

解释：

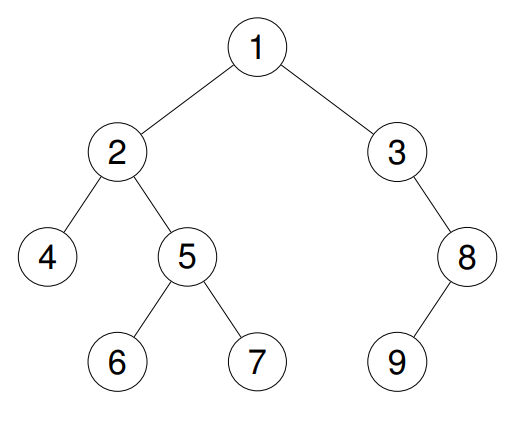
示例 3：

输入：root = []

输出：[]

示例 4：

输入：root = [1]

输出：[1]

二、源代码（部分)

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/
void preorder(struct TreeNode* root, int* res, int* resSize) {if (root == NULL) {return;}res[(*resSize)++] = root->val;preorder(root->left, res, resSize);preorder(root->right, res, resSize);
}int* preorderTraversal(struct TreeNode* root, int* returnSize) {int* res = malloc(sizeof(int) * 2000);*returnSize = 0;preorder(root, res, returnSize);return res;
}

三、题目解析

1. 函数功能概述

该代码实现了二叉树的前序遍历（Preorder Traversal），即按照 “根节点→左子树→右子树” 的顺序访问二叉树的所有节点，并将节点值按访问顺序存储在数组中返回。

2. 核心函数解析

preorder 函数（递归辅助函数）作用：递归实现前序遍历，将节点值存入结果数组。参数说明：
- struct TreeNode* root：当前遍历的二叉树节点（初始调用时为根节点）。
- int* res：存储遍历结果的数组。
- int* resSize：指向结果数组当前元素个数的指针（用于动态记录数组长度）。
逻辑：
1. 若当前节点 root 为 NULL（空节点），直接返回（递归终止条件）。
2. 否则，将当前节点值 root->val 存入结果数组 res 的第 *resSize 位，然后将 resSize 自增（记录新元素）。
3. 递归遍历当前节点的左子树：preorder(root->left, res, resSize)。
4. 递归遍历当前节点的右子树：preorder(root->right, res, resSize)。
preorderTraversal 函数（主函数）作用：初始化结果数组，调用递归函数完成遍历，并返回结果。参数说明：
- struct TreeNode* root：二叉树的根节点。
- int* returnSize：指向一个整数的指针，用于输出遍历结果的元素个数（供调用者获取数组长度）。
逻辑：
1. 分配一个大小为 2000 的整数数组 res（题目假设二叉树节点数不超过 2000，避免动态扩容的复杂度）。
2. 初始化 returnSize 为 0（初始时结果数组为空）。
3. 调用递归函数 preorder 开始遍历，将结果存入 res，并通过 returnSize 记录长度。
4. 返回结果数组 res。

四、实验总结

1. 实验目的

实现二叉树的前序遍历，验证递归算法在二叉树遍历中的正确性和可行性。

2. 实验原理

前序遍历的核心规则是 “根→左→右”：先访问当前节点，再递归遍历左子树，最后递归遍历右子树。通过递归的方式，利用函数栈自动维护遍历顺序，无需手动管理节点访问的先后关系。

3. 实验结果分析

正确性：对于任意二叉树（包括空树、只有根节点的树、完全二叉树、斜树等），代码均能按 “根→左→右” 的顺序输出节点值。例如：对二叉树 1(NULL, 2(3, NULL))（根为 1，右子树为 2，2 的左子树为 3），遍历结果为 [1, 2, 3]，符合预期。
时间复杂度：O(n)，其中 n 为二叉树的节点数。每个节点被访问一次，递归过程中无重复操作。
空间复杂度：
- 数组空间：O(2000)（固定大小，实际可优化为动态扩容）。
- 递归栈空间：最坏情况下（斜树，所有节点只有左子树或右子树），递归深度为 n，空间复杂度为 O(n)；平均情况下为 O(log n)（平衡二叉树）。

4. 优缺点

优点：
1. 实现简洁直观，直接反映前序遍历的逻辑（根→左→右），易于理解和维护。
2. 递归无需手动管理栈，减少了代码复杂度。
缺点：
1. 依赖函数递归栈，当二叉树深度过大（如超过系统栈容量）时，可能导致栈溢出。
2. 结果数组大小固定为 2000，若节点数超过此值会导致数组越界（需优化为动态扩容，如使用 realloc）。