变分自编码器（VAE）的原理方法（一）

变分自编码器（VAE）的原理方法（二）

关键词：
变分自编码器（VAE）

一、说明

无论是概率人工智能爱好者、深度学习专家，还是现代人工智能领域的先驱，变分自编码器VAE 都对他们极具吸引力。它的应用范围涵盖数据生成、异常检测以及表征学习等，涉及图像、音频、文本和信号处理等多个领域。基于 VAE 的论文也经常出现在如今的 NeurIPS 会议上。在深入学习 VAE 之前，让我们先来了解一下密度估计。
如果说有一类模型在今天仍然像十多年前刚问世时那样具有现实意义，那非变分自动编码器（VAE）莫属。

二、密度估计

密度估计是许多人工智能系统的核心。给定一个产生数据的随机现象，密度估计涉及借助一些已采集的样本数据来猜测该现象的潜在概率密度函数（PDF ） 。

假设我们有观测值$x_1,x_2\dots$，我们的目标是猜测生成该数据集X 的潜在PDF(概率密度函数)$p(x)$。一旦我们做到了这一点，我们就能了解生成这些数据的随机现象，并可以模拟它，即我们可以自己生成更多的训练数据。如果数据集带有标签，我们可以通过估计条件分布p(给定x 的 y)来进行预测！

2.1 非参数密度估计？

1)直方图估计法
猜测概率密度函数 (PDF) 最直接的方法是估计点x处的概率密度与 x附近观测值的数量成正比。如果 x周围的观测值很多，那么该点的概率密度就高，反之亦然。实际上，一种古老而直观的概率密度估计方法是使用直方图。我们只需将样本空间划分成一系列小区间（区间越小越好），然后用落入对应区间的训练数据点的比例来近似每个区间中心的概率密度！就是这么简单！而且效果也很好。
2）KDE核密度估计
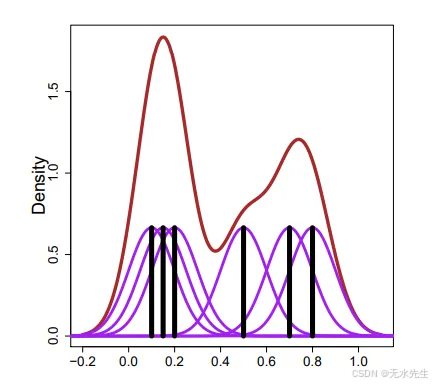
核密度估计( KDE ) 是一种类似的方法，但略微复杂一些。它将每个数据点$x_i$平滑成小的轮廓线，然后将所有这些轮廓线相加，得到最终的密度估计值。在下图所示的示例中，有 6 个数据点（黑色垂直线）。KDE 首先将每个数据点平滑成一个紫色的密度凸起，然后将它们相加，得到最终的密度估计值——棕色曲线！

3.2 参数密度估计

以上两种方法都属于“非参数”类型。我们不对潜在分布的类型做任何假设，仅使用数据集X进行估计。其中不涉及任何“参数”。在参数方法中，我们假设某种分布类型（例如高斯分布），然后通过观察数据集来估计该分布的参数（即均值和方差）。我们通过寻找使观测到这些数据点的似然性最大化的参数来估计密度……没错，这就是最大似然估计 ( MLE)方法。这些参数可以是泊松分布的 λ 值、高斯分布的μ均值/σ^2方差组合，甚至是线性回归模型的权重。一旦我们估计出这些参数，我们就知道如何进行密度估计，并且可以将这些知识用于回归、分类、聚类、异常值检测、生成等任务。

三、变分自编码器（VAE）原理

在本部分，我们将重点讨论如何估计生成过程中的密度。Dall-E 和其他现代人工智能模型都建立在本文使用的核心概念之上。具体来说，我们将看到看似简单的正态分布如何在生成式人工智能中发挥重要作用，这种方法被称为变分自编码器 (VAE)。为了理解 VAE，我们首先来了解一下自编码器，这是一个相当简单的概念。

这是概率人工智能系列文章的倒数第二篇，面向希望了解人工智能模型背后的数学原理的从业者。阅读本文的前提是具备随机变量、概率分布及其参数和概率密度函数（PDF）等基本概念，这些概念已在本篇文章中介绍。最好也具备贝叶斯推断的基本概念。

自编码器是一种神经网络，它简单地学习如何将输入复制到输出。它由一个编码器和一个解码器组成。编码器将输入压缩成一个（更小的）潜在空间表示，解码器则尝试从潜在空间重建原始输入。你可能会觉得这有点傻——既然可以直接使用输入，为什么还要做这么多工作呢？实际上，我们根本不关心自编码器的输出，我们关心的是中间部分，也就是潜在空间，有时也称为Z 空间。由于这个空间本身就是低维的，因此它可以完美地充当“数据压缩工具”——一个数据压缩工具！

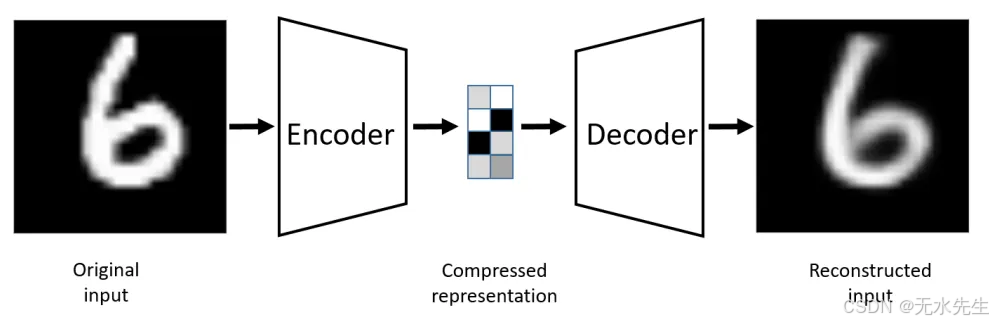
常规自编码器架构

因此，我们将（例如）1000维数据输入编码器，得到（例如）50维输出，该输出保留了大部分核心信息。基本上，输入被转换成一个50维编码向量，其中每个维度代表输入的某个（已学习的）属性。这50个维度中的每一个都是一个浮点值。将这个编码向量输入解码器，即可得到一个1000维输出，该输出是对原始输入的（近似）重构。虽然我们可能无法得到完美的重构——这是可以接受的。

编码器和解码器都是神经网络。前者由一组权重θ参数化，后者由一组权重φ参数化。当然，我们更感兴趣的是中间层，它除了作为压缩模块之外，还能发挥其他重要作用。你可能还记得，在上一篇文章中，我们学习了潜在变量。这些变量无法直接观测，但它们会影响任何观测到的数据。例如，人类的健康状况可以直接观测，但影响我们健康的基因却无法直接观测。通过更深入地研究相关的潜在变量，我们可以了解任何数据集（包括人体）的许多信息。自编码器的中间层揭示了输入图像的潜在属性！

你看，许多复杂的分布都可以通过利用其潜在的属性来估计。例如，请看下图左侧的图像。直接估计该分布的概率密度函数 (PDF) 比较困难。但如果​​你看它右侧的图像，你会发现该分布实际上是三个高斯分布的简单混合。混合比例由我们称之为Z 的潜在变量决定。这是一个简单的例子，展示了潜在变量的强大功能。

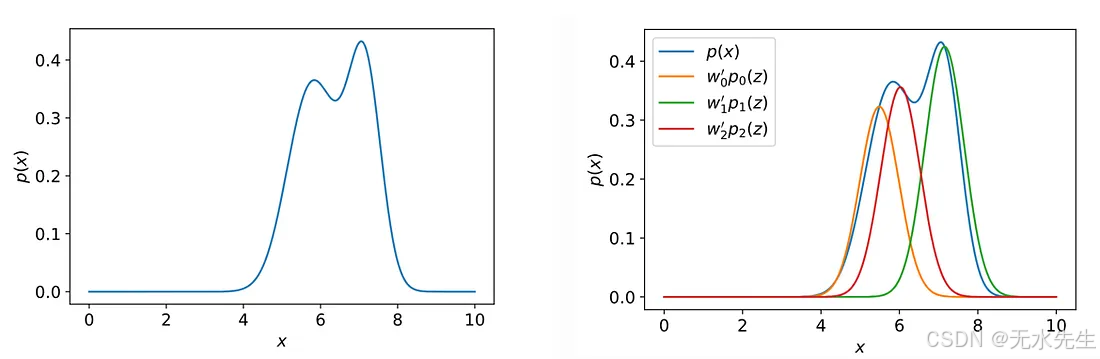
示例展示了潜在变量的强大作用

考虑一个更复杂的情况：使用包含大量人脸的完整数据集来训练自编码器。这里，潜在维度Z可以是一组面部特征，例如：人是微笑还是皱眉，是否有胡须，是否佩戴墨镜，头发颜色等等。自编码器的中间层捕获这些潜在特征，并将它们编码为浮点数（FP）——每个潜在维度对应一个浮点数。这些潜在特征组合起来，最终生成解码器的输出（重建的人脸）。由于潜在特征的数量非常少（上述例子中只有 50 个，而不是 1000 个），因此也很容易处理！事实上，我们稍后会尝试组合这些潜在特征，生成一些有趣的人脸组合。请注意，潜在特征/维度/属性在这里可以互换使用。

自编码器的这些潜在特征不仅对数据压缩有用，它们还可以用于异常值检测。因为模型没有学习压缩异常值，训练数据中不存在这些异常值，所以无法轻易地重建异常值）。但更重要的是，它们还可以进行数据生成！不过，要实现这一点，你需要对自编码器的设计稍作调整。首先，我们不再将每个潜在维度视为单个（浮点）值，而是假设它们服从某种概率分布！但首先，让我们了解一下为什么基本形式的自编码器不能用作生成模型。

四、自编码器在“生成”方面的局限性

传统的自编码器会将每个输入图像映射到“ Z ”空间（即潜在空间）中的不同点。这样，在需要时就能非常轻松地重建相同的图像。虽然我们并没有明确设计这种映射方式，但这正是自编码器在训练过程中学习的方式。这种映射几乎就像一个查找表。Z空间并非连续，它们之间存在许多间隙。在进行图像重建时，这种方式是可以接受的（而且确实是正确的做法），但它不适用于生成训练数据中从未出现过的全新图像。你能猜到为什么吗？

常规自动编码器的局限性

是的！这是由于Z空间中的间隙造成的。请看上图，其中自编码器已在 MNIST 数据集（包含 0 到 9 的一系列数字图像）上训练完成。将编码可视化为二维潜在空间，可以发现其中形成了被大量空白区域隔开的明显簇。当我们从这个Z空间创建新图像时，这些间隙代表什么呢？解码器会生成一些不切实际的输出，因为它不知道如何处理潜在空间中的这部分区域。在训练过程中，它从未见过来自这部分区域的编码向量。因此，我们需要对设计进行一些调整来帮助它！

五、VAE——快速直觉

在训练自编码器时，我们并没有将输入图像映射到Z空间中的一个点，而是强制它略微扩散开来。我们想要的不是Z空间中的一个点，而是一个在均值周围有大片扩散区域、周围有一些小斑点的分布。我们还确保画布本身很小，也就是说，Z空间所能占据的整个区域应该非常小（尽可能小，同时还要保证图像之间仍然彼此区分）。这个小画布确保了不同的图像表示在潜在空间中彼此靠近，而不是分散在有很多间隙的大片区域。这两个条件共同确保了Z画布上近乎连续的“绘画” 。现在，就可以生成新的图像了！

对于第一个条件，我们让 Z 空间映射成为一个以均值为中心的分布（方差较小的 Gaussian 分布），而不是点对点映射。对于第二个条件，我们确保 Z 空间的整体分布尽可能接近一个小 Gaussian 分布（单位 Gaussian 分布）。这使得所有数据点都趋于一致。这就像一个分布正则化器！

第一个条件是我们熟悉的图像重建故事，只不过加入了一些“光滑”元素。假设我们仍然经历从1000维到50维再到1000维的转换过程。在常规的自编码器中，编码器处理后会得到一个50维的向量。而在变分自编码器（VAE）中，我们会生成一个均值向量和一个方差向量（Z的每个维度对应一个向量，总共50个）。这种“光滑”无疑减少了数据间隙，但它还有另一个显著的优势——它为解码器提供了更多的数据——来自均值附近任何位置的样本都会与原始输入非常相似，同时又存在一些细微的差异！

虽然这能提供一个很好的直观理解，但我们不妨也从更正式的角度来探讨这个问题。让我们来了解一下VAE中的关键角色。对于忙碌的应用人工智能爱好者来说，如果他们想学习概率人工智能，最大的障碍（在我看来）并非数学（这并不奇怪），而是那些可能让他们偏离正轨的符号和语义。

六、构建VAE

先别管自编码器，我们从零开始。设X为图像数据集，$x_1,x_2\dots$为单个图像。每张图像由一系列像素值组成。这些像素值组合起来决定了图像的外观。

• p(x)是x的分布，它是所有相关像素的联合分布。如果我们知道这个分布，就可以生成任何我们想要的图像。然而，直接获取这个分布却非常困难。为什么呢？假设图像尺寸为 1048×720 像素，每个像素有 3 种颜色，每种颜色有 256 个值，那么可能的图像数量为 (256×3)¹⁰⁴⁸*⁷²⁰。图像的数量是不可数的。因此，这个分布在实际应用中是无法研究的！
• 实际上，图像的某些特性简化了我们的工作。例如，相邻像素通常颜色相似。生成模型的任务就是捕捉像素之间的这些依赖关系。模型还需要确保对于真实图像， p(x)值较高；对于非真实图像，p( x )值较低。更实际的期望是，模型应该能够通过学习训练样本中的概念来生成新的图像。当然，要实现这一点，我们需要一个庞大的训练数据集！
• 正如我们之前讨论的，较小的潜在空间“ Z ”通常有助于解决这类问题。因此，与其费力理解p(x)，不如尝试创建一个更简单的概率分布p( 给定输入x时z的概率)，即p(z|x)。虽然一旦我们知道了p(z|x)就很容易处理，但遗憾的是，要获取p(z|x)本身却非常困难。我们可以做的是训练一个神经网络，得到一个足够接近p(z|x)的分布q(z|x) （没错——这个神经网络就是我们自编码器的编码器部分）。假设这个分布是高斯分布是合理的（当然，我们也可以进行实验）。
• 因此，编码器需要为每个输出维度提供一个均值/方差组合。如果Z是 50 维的，那么编码器应该提供50 个均值和 50 个方差。设编码器由φ参数化，φ 是它的权重集（我们将对其进行调整）。值得注意的是，这里的φ并非高斯分布的均值/方差组合，而是我们将要调整的编码器的权重。调整完成后，这些权重会输出输入图像的均值/方差组合，也就是说，编码器学习将输入x映射到分布q的参数。从这个意义上讲，φ参数化了分布，因此可以将编码器输出的分布写成q φ (z|x)。有时，我们直接使用q(z|x)，这样更容易阅读。
• 因此，编码器以x作为输入，输出q(z|x)分布的均值/方差组合。具体来说，编码器并非像通常那样对z的每个维度进行点编码（即返回一个浮点数） ，而是返回每个维度的分布，也就是返回一个包含均值和方差的向量。该向量的长度等于z的维度。好了，编码器完成！
  接下来，我们从上述q(z|x)中“采样”一个潜在向量，记为z 。因此，z是从潜在分布q(z|x)中抽取的一个样本。如果编码器训练良好，那么z应该包含描述x 的几乎所有信息。

现在我们的任务是从远小于原图的z值重建原图x。由于我们讨论的是概率模型而非确定性模型，我们需要的是概率分布p(x|z)，而不是直接重建x。我们需要训练另一个神经网络，使其接收z 值并给出p(x|z) 。是的，这对应于我们的解码器。然后，我们可以通过（例如）取该分布的均值来重建原图，得到图像x’。如果解码器也训练得当，那么x’将非常接近原图x。事实上，我们稍后会看到，我们的损失函数正是(xx’)²与其他项的组合。假设解码器网络的权重由θ参数化。因此，正式的表达式是pθ (x|z)，但我们通常会使用p(x|z)。

注意，对于图像处理，神经网络的每个维度都对应一个像素值。例如，解码器需要为每个像素输出一个值。解码器的输入是z，假设它是 50 维的。它的输出应该是x’，其维度与x相同，即 1000 维。因此，解码器的最后一层应该输出 1000 个值——每个像素对应一个值。这些值实际上是高斯分布p(x|z)的均值。这些像素值组合起来就形成了x’。

等等！为什么解码器只输出高斯分布的“均值”像素值？它难道不应该也输出高斯分布的方差吗？毕竟，解码器的目标是生成高斯概率分布p(x|z)，而我们需要均值和方差！为什么不生成 1000 个方差呢？好吧，我们暂时先搁置这个问题，因为本文的“实用 VAE”部分会详细讨论。现在，我们先不要让实际应用方面的内容干扰我们的主要流程。

解码器部分也完成了，但我们再回到编码器部分吧！

如前所述，我们还需要确保编码器输出的潜在分布绘制在一个较小的画布上。让我们为该分布设置一个“单位高斯先验” 。如您所知，我们在观测任何数据x之前设置先验。因此，潜在变量z的概率分布p(z)服从N(0,1)分布。显然，这是一个多变量分布，其维度与z 的维度相同。我们的后验分布为p(z|x)，其中x是观测数据。如前所述，由于p(z[x])难以计算，我们使用近似后验分布q(z|x)。在所有计算中，我们都使用这个近似后验分布，而不是实际的后验分布。
现在编码器和解码器一起训练，我们得到最优神经网络权重φ和θ。一旦模型训练完成，编码器和解码器模块就开始输出每个输出维度的均值/方差组合。由此，我们从编码器获得所需的分布，即q φ (z|x) ……然后从中采样z并将其输入解码器，解码器生成p θ (x|z)……最终由此生成最终输出。

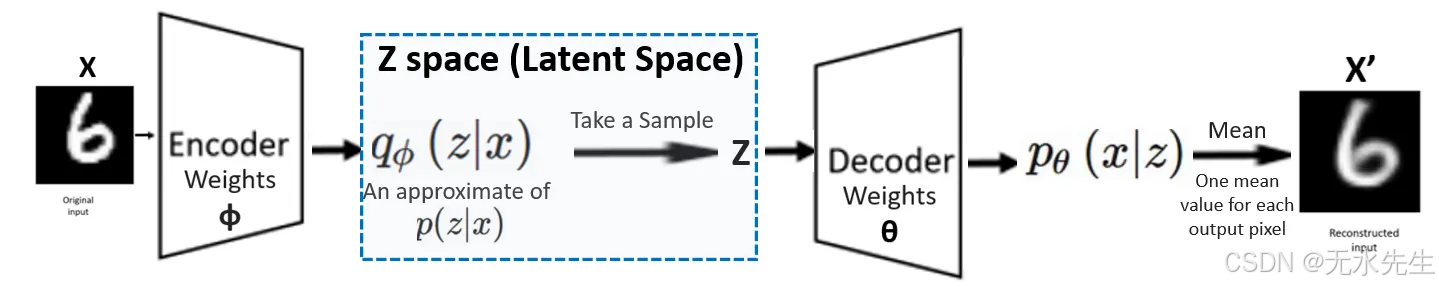
VAE最终架构

最后一点是——我们应该使用什么损失函数来联合训练编码器-解码器网络，以获得最佳的φ和θ值！我们知道这个损失函数肯定包含重构误差项x- x’。还有什么需要注意的吗？我们也讨论过它应该惩罚qφ (z|x)与单位高斯分布之间的偏差。还有其他需要注意的地方吗？与其凭直觉来判断，不如使用我们可靠的老朋友——最大似然估计（MLE）来找到最佳的损失函数？