力扣-环形链表

核心思路

判断链表是否有环的核心思路是 “利用速度差来制造相遇”。

我们将这个思想应用到链表上：

定义两个指针，一个 慢指针 (slow) 和一个 快指针 (fast)。慢指针每次只移动一步，快指针每次移动两步。如果链表 没有环，快指针会比慢指针先到达链表的末尾（NULL）。

如果链表 有环，快指针会进入环内并开始 “兜圈子”。由于它的速度比慢指针快，它最终一定会在环内的某个节点 “追上” 慢指针。

结论：如果在遍历过程中，快慢指针指向了同一个节点，就说明链表有环。

 

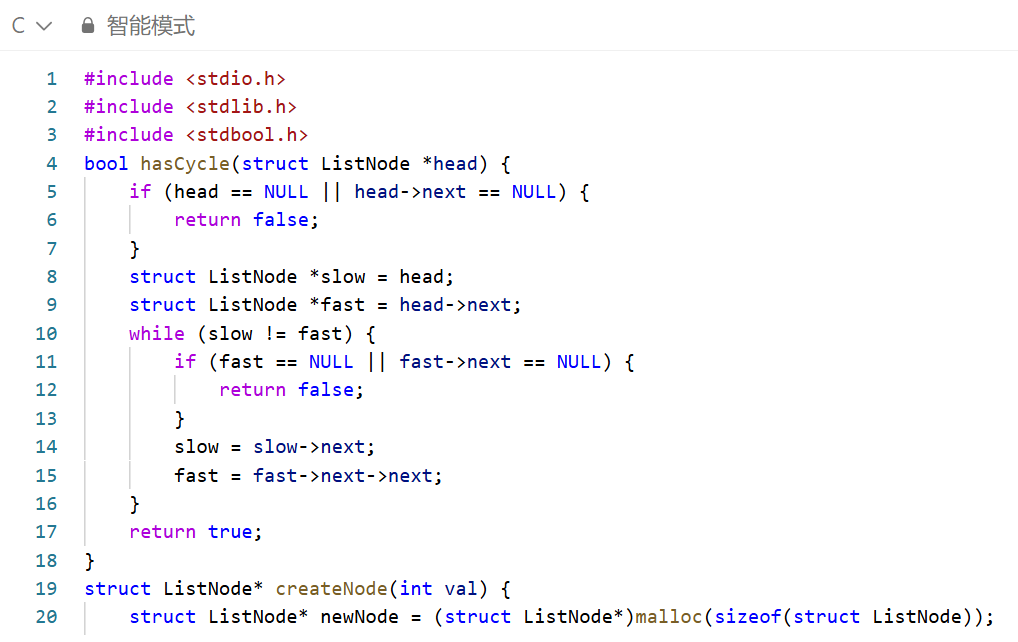
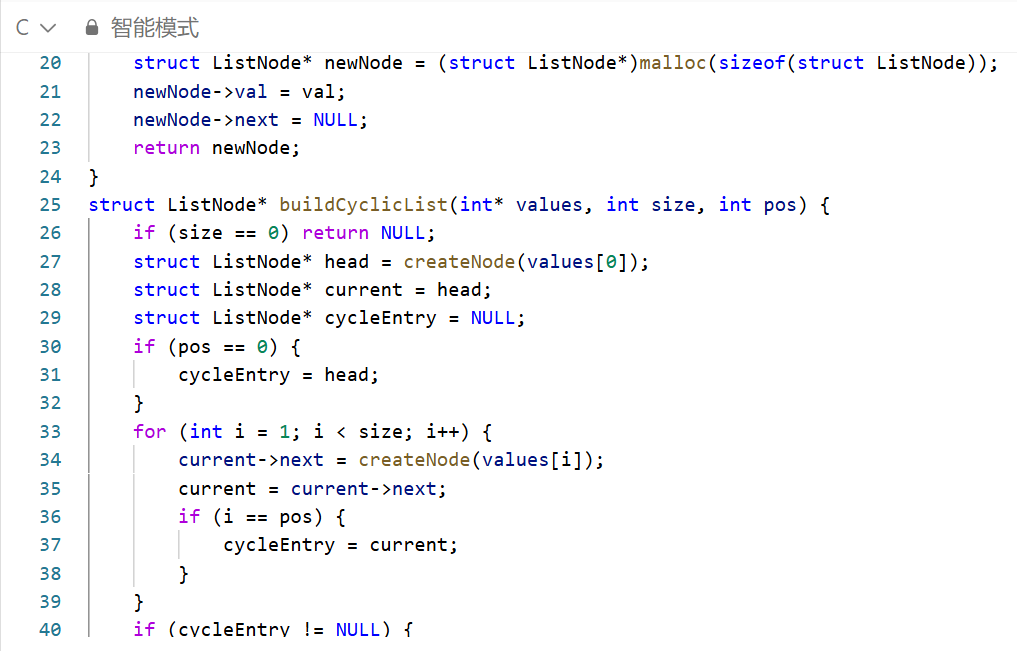
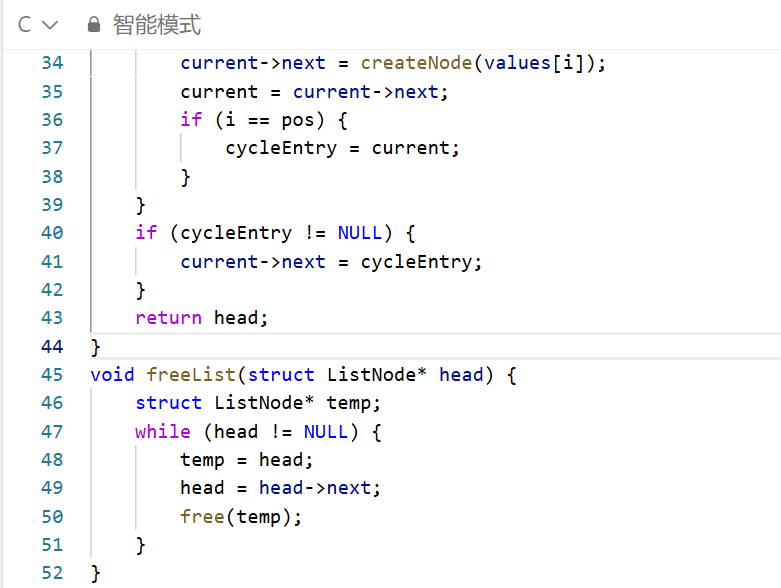
方法：快慢指针法 (Floyd's Tortoise and Hare Algorithm)

这是解决此问题最经典、最高效的方法，也被称为 “Floyd 判圈算法”。

初始化：

慢指针 slow 和快指针 fast 都指向链表的头节点 head。

为了算法启动，可以将 slow 初始化为 head，fast 初始化为 head->next，这样可以避免初始状态下 slow == fast。

遍历与移动：

进入一个循环，循环的条件是 slow != fast。

在循环内部，慢指针 slow 向前移动一步 (slow = slow->next)。

快指针 fast 向前移动两步 (fast = fast->next->next)。

关键检查：在移动快指针之前，必须先检查 fast 和 fast->next 是否为 NULL。如果是，则说明链表走到了尽头，不存在环。

判断结果：

如果循环因为 slow == fast 而退出，说明两个指针在环内相遇，链表存在环，返回 true。

如果循环因为快指针到达 NULL 而退出，链表不存在环，返回 false。

优点

快慢指针法之所以被推崇，是因为它具有显著的优点：

时间效率高：

时间复杂度为 O(n)。其中 n 是链表节点的数量。如果链表无环，快指针会在 n/2 步内到达末尾。如果链表有环，两个指针相遇的时间取决于环的长度，最坏情况下为 O(n)。

空间效率极高：

空间复杂度为 O(1)。

该算法只使用了两个额外的指针，不占用任何与链表长度成比例的额外存储空间。这使得它在处理大规模数据时非常节省内存。

实现简洁优雅：

算法逻辑直观，代码实现简单，只需要一个循环和几个指针操作。

结论

正确性：快慢指针法是判断链表是否存在环的 正确且可靠 的方法。其正确性基于一个简单的事实：在一个封闭的环内，速度快的物体必然会追上速度慢的物体。

最优性：在时间和空间复杂度上，快慢指针法都是解决该问题的 最优解法。它完美地平衡了时间和空间开销。

适用性：该方法不仅可以判断是否存在环，还可以进一步用于 寻找环的入口节点 和 计算环的长度，是处理链表环相关问题的基石。

总结：对于 “判断链表是否有环” 这一问题，快慢指针法（Floyd's Algorithm）是首选的、标准的解决方案，因为它高效、节省空间且易于实现。