当前位置：首页 > news >正文

MATLAB基于RBF神经网络与DE-NSGAII算法的钢轨闪光焊工艺参数优化

news 2025/11/17 7:54:24

一、引言与研究背景

问题重要性：
- 钢轨闪光焊是高速、重载铁路无缝线路建设的核心工艺，其接头质量直接关系到铁路运输的安全与平稳。
- 焊接接头存在的典型缺陷（如灰斑、未焊合、过热等）与工艺参数设置密切相关。
传统优化方法的局限性：
- 试验法（如正交试验）：成本高昂、周期长，难以全面覆盖高维参数空间。
- 单目标优化：焊接质量是典型的“多指标”问题（如拉伸强度、疲劳性能、硬度分布等），这些指标往往相互冲突，单目标优化无法获得均衡解。
- 标准遗传算法/NSGA-II：在处理复杂、高维、非凸的帕累托前沿时，可能陷入局部最优，且收敛速度有待提升。
研究创新点：
- RBF神经网络作为代理模型：用少量实验数据，构建工艺参数（输入）与质量指标（输出）之间高精度的非线性映射关系，替代耗时耗力的物理实验或有限元仿真，为优化算法提供快速目标函数评估。
- DE-NSGA-II混合优化算法：
  - 差分进化（DE）：强大的全局探索能力，变异操作能有效维持种群多样性。
  - NSGA-II（非支配排序遗传算法）：经典的多目标优化框架，利用快速非支配排序和拥挤度计算来寻找分布均匀的帕累托最优解集。
  - 融合优势：将DE的变异、交叉策略引入NSGA-II，增强算法跳出局部最优和收敛到全局帕累托前沿的能力。

二、核心理论与关键技术

钢轨闪光焊工艺分析
- 关键工艺参数（输入变量）：次级电压、闪光速度、闪光留量、顶锻压力、顶锻留量、顶锻速度、烧化量等。
- 质量评价指标（输出目标）：落锤试验次数（衡量韧性）、拉伸强度、疲劳寿命、焊缝冲击韧性、硬度（HAZ与母材的硬度比）等。这些目标通常是相互矛盾的（例如，提高强度可能降低韧性）。
RBF（径向基函数）神经网络
- 原理：一种三层前馈网络，通过径向基函数（如高斯函数）作为隐层激活函数，实现从输入到输出的非线性映射。
- 优势：结构简单、训练速度快、具有全局逼近能力，非常适合构建高精度的代理模型。
- 建模流程：
  1. 数据收集：通过历史数据、正交试验或有限元仿真获取样本数据集 {X, Y}。
  2. 网络训练：确定隐层中心（如K-means聚类）、宽度（如最近邻法）和输出层权重（如最小二乘法）。
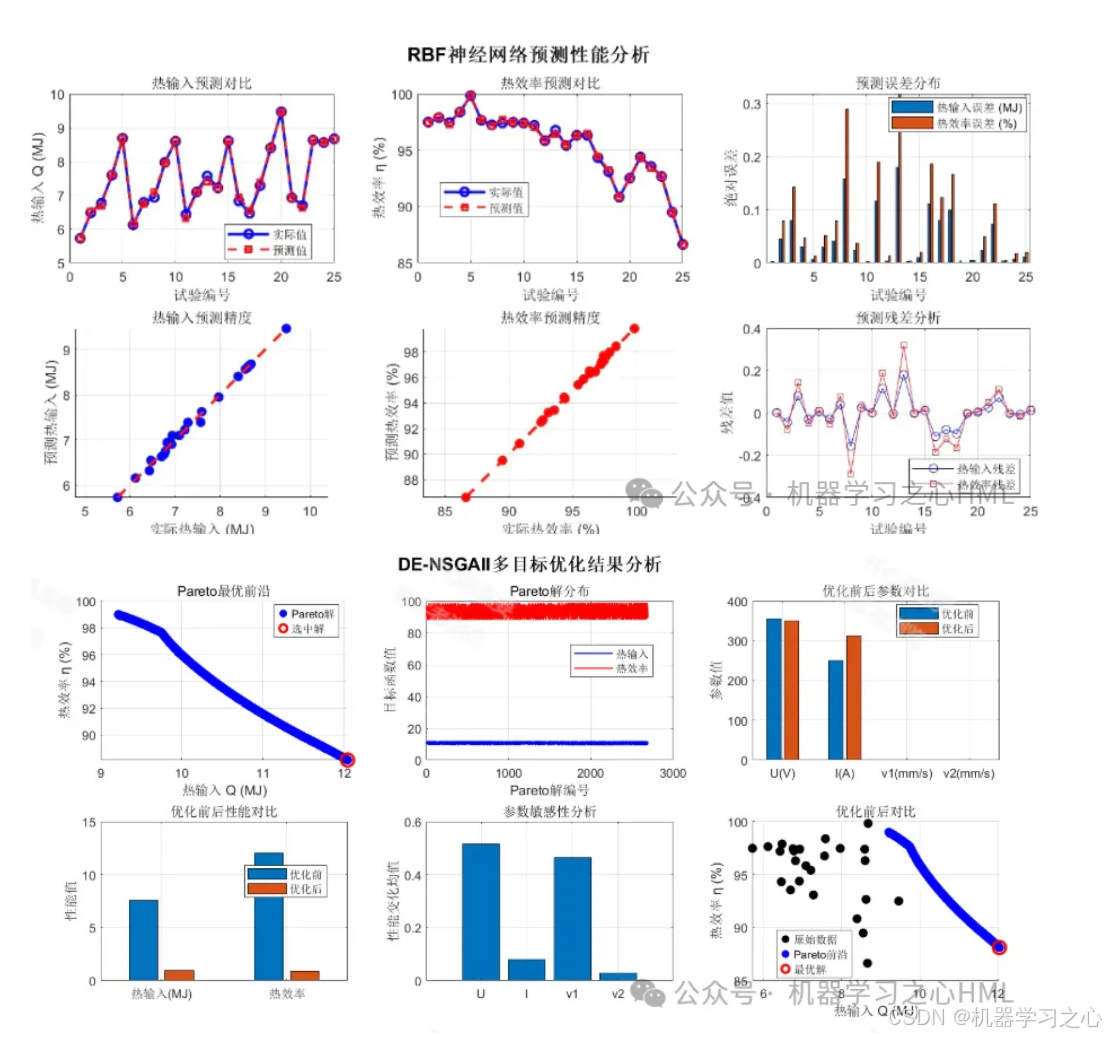
  3. 模型验证：使用留出法或交叉验证法评估模型的预测精度（如R², RMSE）。
DE-NSGA-II混合多目标优化算法
- 差分进化（DE）操作：
  - 变异：对于每个个体 ( \vec{x}i )，生成变异向量 ( \vec{v}i = \vec{x}{r1} + F \cdot (\vec{x}{r2} - \vec{x}_{r3}) )，其中F为缩放因子。这种基于差分的变异具有强大的探索能力。
  - 交叉：将变异向量 ( \vec{v}_i ) 与目标向量 ( \vec{x}_i ) 进行交叉，生成试验向量 ( \vec{u}_i )。
- NSGA-II框架：
  - 快速非支配排序：将种群个体划分为不同等级的非支配层。
  - 拥挤度计算：衡量同一非支配层中个体周围的密度，以保持解集的多样性。
- 混合策略：用DE的变异/交叉操作替代NSGA-II中原有的模拟二进制交叉（SBX）和多项式变异（PM），或者将DE作为一种额外的搜索算子嵌入循环中。这能有效提升算法的全局搜索性能和收敛速度。

三、整体优化模型构建流程

阶段一：数据准备与代理模型构建

实验设计与数据采集：采用拉丁超立方采样或中心复合设计等实验设计方法，在工艺参数可行域内生成有限的样本点，并通过实际焊接实验或高保真仿真获取对应的质量指标数据。
RBF代理模型训练与验证：
- 将样本数据分为训练集和测试集。
- 使用训练集数据训练多个RBF神经网络，每个网络对应一个质量指标（如一个RBF网络预测“落锤次数”，另一个预测“拉伸强度”）。
- 利用测试集验证模型的预测精度，确保其能够可靠地替代真实物理过程。

阶段二：DE-NSGA-II多目标优化

优化问题数学描述：
- 决策变量：闪光焊工艺参数集合 X = [x1, x2, ..., xn]。
- 目标函数：Minimize/Maximize F(X) = [f1(X), f2(X), ..., fm(X)]，其中 fi(X) 由训练好的RBF神经网络计算得出。
- 约束条件：工艺参数的上下限、质量指标的合格范围等。
DE-NSGA-II算法流程：
1. 初始化：在决策空间内随机生成初始种群。
2. 评价：使用训练好的RBF代理模型，快速计算种群中每个个体的所有目标函数值。
3. 主循环（迭代直至满足终止条件）：
  - 选择：根据非支配排序和拥挤度比较，选择父代。
  - DE操作：对父代种群执行差分进化的变异和交叉操作，生成子代种群。
  - 合并：将父代与子代种群合并。
  - 环境选择：对合并种群进行非支配排序和拥挤度计算，选出新一代种群。
4. 输出：获得一组帕累托最优解集（Pareto Front），即一组无法在不让其他目标变差的情况下使任一目标变好的工艺参数方案。