深度学习周报(11.10~11.16)
目录
摘要
Abstract
1 文献总结
1.1 GPT-1 与 GPT-2 对比
1.2 拓展
1.2.1 GELU 与 ReLu
1.2.2 零样本任务
1.2.3 BPE
2 shor算法代码梳理
2.1 经典算法
2.2 shor算法
3 总结
摘要
本周首先总结了前面阅读的两篇文献,对比了GPT-1与GPT-2的各方面差异,同时对GELU与ReLu激活函数的区别、零样本任务以及BPE等知识点进行了拓展;其次梳理了shor算法的代码,包括其经典实现与量子实现,深入理解了其过程。
Abstract
This week, I first summarized the two previously read papers, comparing the differences between GPT-1 and GPT-2 in various aspects. Additionally, I expanded my knowledge on topics such as the distinctions between the GELU and ReLU activation functions, zero-shot tasks, and Byte Pair Encoding (BPE). Secondly, I reviewed the code for Shor's algorithm, including its classical and quantum implementations, gaining a deeper understanding of its process.
1 文献总结
1.1 GPT-1 与 GPT-2 对比
两者在核心思想与目标、模型架构与训练过程、执行方式、能力与影响上都有所不同。
在核心思想与目标上,GPT-1 明确知道要解决的是什么具体任务(任务感知),一开始通过预训练得到一个强大的初始化模型,然后通过微调来适配具体任务;而 GPT-2 作为一个通用的系统,本身不针对任何具体任务调整(任务不可知),它面对的任务完全由输入时的提示或指令来定义。
在模型架构与训练过程上,GPT-1 包括 1.17 亿参数 ,采用标准初始化、40000 BPE 的词汇表以及 512 tokens 的上下文长度,层归一化位于每个子块之后,在 BooksCorpus 数据集上进行训练;GPT-2 最大包括 15.42 亿参数,按残差层数进行缩放初始化,采用 50257 字节级BPE,能处理任何 Unicode 字符串,无需预处理,上下文长度增加至 1024 tokens,能捕捉更长的依赖关系,其层归一化移至每个子块的输入处,并进行最终层归一化,训练更稳定,且在从Reddit高赞链接收集的 WebText 数据集上训练,质量更高更多样。
执行方式是两者最关键?的差异,GPT-1 为每个任务设计一个特定的输入格式,并在预训练模型后添加一个简单的线性输出层,然后用有标签数据对整个模型进行微调;而 GPT-2 不进行任何微调。将任务描述和示例作为自然语言提示,直接输入给模型,让模型通过生成文本来完成任务。
在能力与影响上,GPT-1 确立了 Transformer Decoder+生成式预训练+微调 这一NLP新范式的有效性,泛化能力强,但依赖高质量的标注数据进行微调;而 GPT-2 提出了 “语言模型即多任务求解器” 的革命性设想,泛化能力更强,它展示了前所未有的零样本泛化能力,表明模型能从数据中学习到通用的推理模式,还证明了模型规模的极端重要性,直接引领了大模型时代的到来。此外,由于担心滥用风险(如生成假新闻、恶意内容等),GPT-2最初仅发布了小模型和示例,引发了关于AI伦理的空前讨论。
1.2 拓展
1.2.1 GELU 与 ReLu
GELU(高斯误差线性单元)是一个在现代深度学习,尤其是在 Transformer 模型中广泛使用的激活函数。
它本质上是一种更平滑的 ReLU。ReLU主要基于输入的符号(正或负)进行开关;GELU则基于输入的值,对其进行加权。值越大,被开启或保留的权重就越高;值越小,被关闭或缩小的权重就越高,它不是非黑即白的,而是一个平滑的过渡。
ReLU在 时是线性增长,在
时完全关闭;Leaky ReLU / ELU,在
时有一个非零的输出,通常是线性的或渐进饱和的;而 GELU 在所有区域都是平滑的曲线,在
时,输出并不完全是零,而是一个被平滑压制后的值;在
时,也并非立刻线性增长,而是有一个平滑的过渡。这种特性使其更符合自然的概率分布。
1.2.2 零样本任务
零样本任务(Zero-Shot Task)指的是一个模型在未经任何特定任务的数据训练或微调的情况下,直接执行该任务的能力,换句话说,它是指模型在测试阶段能够处理在训练阶段从未见过类别的任务。其中零样本即指模型没有见过这个任务的任何(输入,输出)配对示例。
零样本学习的核心思想是通过某种形式的辅助信息(如属性、描述、词向量等)来建立已知类别(训练类别)和未知类别(测试类别)之间的联系,从而使得模型能够识别或处理未知类别。
它通常采用两种方法。第一种是基于属性的方法,每个类别(包括已知和未知)都用一组属性来表示,模型学习从输入到属性向量的映射,在测试时,对于未知类别的样本,模型预测其属性向量,然后通过与未知类别的属性向量进行比较来分类;另一种是基于嵌入的方法,它将图像(或文本)特征和类别标签都映射到一个共同的嵌入空间,模型学习将输入特征映射到嵌入空间,并且使得同一类别的样本在嵌入空间中靠近,在测试时,未知类别的样本被映射到嵌入空间,然后通过计算与未知类别标签嵌入的相似度来进行分类。
零样本学习可以应用于多种任务,包括但不限于图像分类、文本分类、物体检测、图像生成。
与少样本学习相比,零样本学习完全不提供未知类别的样本,但少样本学习会提供少量样本;与无监督学习相比,零样本学习通常利用辅助信息来连接已知和未知类别,而无监督学习完全不使用标签信息。
1.2.3 BPE
BPE(Byte Pair Encoding, 字节对编码) 是一种数据压缩算法,在 NLP 中用于在单词级和字符级之间找到一个平衡点。它从基础字符(如字母)开始,通过不断合并频率最高的相邻符号对,逐步合并成更常见的子词甚至整个单词来构建词汇表。
GPT-1 采用的是标准 BPE。它的基础单元是 Unicode 码点,这意味着它的基础词汇是所有可能的Unicode字符,数量超过13万个,而在实际操作中,并不会使用全部13万个字符作为起点。它会从一个预定义的、较大的子集(比如包含几万个常见字符)开始进行 BPE 合并,最终词汇表大小为 40000 个合并后的令牌。虽然 BPE 能处理多数未知词,但如果输入中出现一个极其罕见的、不在初始字符集中的 Unicode 字符,模型就会无法处理,从而退回到一个 [UNK](未知)令牌。同时它会为同一个单词的不同形式(如 dog, dog., dog!)分别创建令牌,浪费宝贵的词汇表位置和模型容量
p.s. 码点可以被理解成计算机给每个字符(包括英文字母、中文汉字等)分配的一个唯一数字ID。
GPT-2 采用的是字节级 BPE,它的基础单元是字节。由于计算机中,所有数据最终都表示为字节,任何 Unicode 字符都可以通过 UTF-8 编码转换成 1 到 4 个字节的序列,因此,它的基础词汇表大小固定为 256。这是一个极小且完备的集合。它不再在字符级别进行合并,而是在字节序列上进行合并,同时为了防止像 GPT-1 那样出现低效合并(即 dog, dog., dog!),GPT-2 引入了一个关键规则,即禁止 BPE 跨字符类别进行合并,除了空格(因为空格是一个重要的单词边界信号),最终词汇表大小为 50257 个令牌。由于任何字符串都可以被分解为字节序列,而基础字节只有256个,所以 GPT-2 可以为任何 Unicode 字符串分配一个概率,彻底告别了 [UNK] 令牌。同时它具有更强的稳健性和更高的效率。
2 shor算法代码梳理
2.1 经典算法
不使用量子的代码大致如下所示:
import random
import math
import itertoolsdef period_find_classical(a, N):for r in itertools.count(start=1): #itertools.count(),默认起始点为0,步长为1,对应创建一个从0开始逐渐递增的无限的计数迭代器if (a**r) % N == 1:return rdef shor_algorithm_classical(N):assert(N>0)assert(int(N) == N) #否则报错while True:a = random.randint(0, N-1)g = math.gcd(a, N)if g!=1 or N==1: #此时a与N不互质first_factor = gsecond_factor = int(N/g)return first_factor, second_factorelse: #此时a与N互质r = period_find_classical(a, N)if r % 2 != 0:continueelif a**(int(r/2)) % N == -1 % N: #这个检查很重要!!!continueelse:first_factor = math.gcd(a**int(r/2)+1, N)second_factor = math.gcd(a**int(r/2)-1, N)if first_factor == N or second_factor == N:continueelse:return first_factor, second_factor代码中关于 对 N 取余是否为 -1 的检查是不可忽视的。实际在数学上,我们要求的是
且
,两者中若有一个条件不满足就会出现公式中的两个因子一定有一个为 N 的倍数,从而只能得到平凡因子 N 或 1,得不到非平凡因子。后者要相等,只有
时才成立,而它已经在寻找周期的函数中被设置为从1开始,故此处只检查前者。
另外可以加入检查是否为质数的模块,不过需要进行分解的 N 本身是两个质数的乘积,分解得到的结果也只会是两个质数。
p.s. 对于一个整数而言,平凡因子指的是总是存在的两个因子,即 1 和其本身;非平凡因子指的则是除平凡因子以外的所有因子。
2.2 shor算法
Qiskit 库里内置了 shor类,可以方便地进行整数分解,但为了梳理其过程,还是自行进行了编写。
逆量子傅里叶变换:
def qft_dagger(n):"""生成n量子比特的逆量子傅里叶变换"""qc = QuantumCircuit(n)# 逆QFT电路for qubit in range(n//2):qc.swap(qubit, n-qubit-1)for j in range(n):for m in range(j):qc.cp(-np.pi/float(2**(j-m)), m, j)qc.h(j)return qc.to_instruction()
量子电路:
def quantam_circuit(a, N, m):n_count = m # 计算寄存器n_state = N.bit_length() # 状态寄存器,N.bit_length()返回表示整数 N 所需的最小二进制位数# 创建量子电路(量子比特数,经典比特数)qc = QuantumCircuit(n_count + n_state, n_count)# 初始化计算寄存器为叠加态for q in range(n_count):qc.h(q)# 初始化状态寄存器# n_count是第一个寄存器的长度,也是第二个寄存器起始的索引# 在第二个寄存器的第一个量子比特上应用X门,将其从初始状态|0⟩变为|1⟩qc.x(n_count)# 此处应实现模幂运算,使|x⟩|y⟩ -> |x⟩|y ⊕ a^x mod N⟩# 比较复杂,暂时不写,后续可尝试# 应用逆量子傅里叶变换到计算寄存器qc.append(qft_dagger(n_count), range(n_count))# 测量计算寄存器qc.measure(range(n_count), range(n_count))return qc在原有的两个量子寄存器(计算与状态)之外,代码还设置了一个经典寄存器,用于存储测量结果,进行经典后处理。它的作用可能会与状态寄存器的作用混淆,状态寄存器主要用于存储 的值以辅助计算。
实际的量子电路实现中不会在中间步骤进行测量,所以上周测量状态(第二个)寄存器的操作在实际实现中并不会进行。
同时,纠正上周的一个错误,对计算(第一个)寄存器是进行逆量子傅里叶变换而非量子傅里叶变换。
最终,通过上述代码,得到一个包含测量步骤的量子电路。
周期寻找:
def find_period_quantam(a, N, shots=1024):# 设定计算寄存器大小n_count = 8 # 足够大的寄存器来获得好的精度# 创建并运行量子电路qc = quantam_circuit(a, N, n_count)# 使用模拟器运行backend = Aer.get_backend('qasm_simulator')result = execute(qc, backend, shots=shots).result()counts = result.get_counts()# 从测量结果中提取相位measured_phases = []for output in counts:decimal = int(output, 2)phase = decimal / (2 ** n_count)measured_phases.append(phase)# 使用连分数展开找到周期for phase in measured_phases:# 将相位转换为分数frac = Fraction(phase).limit_denominator(N)r = frac.denominator# 验证周期if a ** r % N == 1:return r# 如果没有找到有效周期,返回最常见的候选phase_counter = Counter()for output in counts:decimal = int(output, 2)phase = decimal / (2 ** n_count)frac = Fraction(phase).limit_denominator(N)phase_counter[frac.denominator] += counts[output]# 返回最可能的周期return phase_counter.most_common(1)[0][0]连分数的形式大概如下所示:
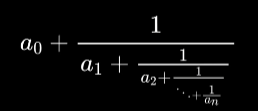
这种形式也被称为简单有限连分数,其中 1 被称为偏分子, 则统称为部分商或偏分母。
连分数展开就是一种将实数表示为上述形式的数学方法,通常被用于寻找实数的最佳有理数近似。
3 总结
本周主要是对前面学习的内容进行回顾总结,拓展学习了新东西,纠正了前面学习的误区,有了更深的理解。
