对于数据结构：链式二叉树的超详细保姆级解析—中

开篇介绍：

Hello 亲爱的朋友们！还记得上一篇博客里，我们一起从 “数组存储的局限性” 切入，一步步搭建起链式二叉树的基础框架吗？我们先是拆解了节点结构体的设计逻辑 —— 为什么必须包含数据域和左右指针域，如何通过指针让零散的节点串联成树；接着手动创建了一棵示例树，看着一个个独立的节点通过left和right指针建立关联，从孤立的 “零件” 变成完整的 “树形结构”；最后花了大量篇幅剖析前序、中序、后序三种递归遍历的核心逻辑，从执行步骤的拆解到生活化例子的类比，再到函数调用栈帧的逐步分析，甚至还手把手带大家实现了 LeetCode 上的遍历真题，就是为了让大家不仅 “会用” 遍历，更能 “看透” 遍历背后的递归本质。

现在回想起来，当时跟着栈帧变化一步步追踪节点访问顺序的过程，是不是既有挑战又很有成就感？当大家终于理清 “前序先根、中序夹根、后序后根” 的差异，甚至能独立写出把遍历结果存入数组的代码时，其实已经打通了链式二叉树的 “入门关卡”。但我必须告诉大家：遍历只是链式二叉树操作体系的 “冰山一角”—— 它更像是我们探索树结构的 “基础工具”，帮我们初步摸清树的节点分布和数据存储规律，而真正在实际场景中解决问题时，还需要更多 “进阶操作” 来支撑。

比如，当我们需要在树中找到某个特定值的节点时，总不能每次都靠遍历打印出来再人工查找吧？这就需要 “节点查找” 操作，让程序能自动定位目标节点的位置；又比如，当我们想评估一棵二叉树的 “深度”—— 比如文件系统中文件夹的嵌套层级、组织架构中管理层级的深度时，就需要 “树的高度计算” 操作，用代码量化树的纵向规模；再比如，在统计某棵树的 “叶子节点数量”（比如统计一棵决策树的最终结果节点、统计一棵水果树的果实节点）时，总不能逐个遍历计数，这就需要专门的 “叶子节点统计” 逻辑，高效筛选出那些左右子树都为空的节点；甚至有时候，我们还需要调整树的结构，比如交换某个节点的左右子树，或者判断两棵树是否完全相同，这些 “结构调整与比较” 的操作，也是链式二叉树应用中绕不开的核心技能。

所以呀，在今天这一篇博客里，我们将从 “基础遍历” 迈向 “深度操作”，带着大家逐一攻克这些实用且高频的链式二叉树操作。我们会延续之前 “原理拆解 + 代码实现 + 场景应用” 的风格：讲解 “节点查找” 时，会对比 “递归查找” 和 “非递归查找” 的差异，告诉大家什么时候用递归更简洁，什么时候非递归更高效；计算 “树的高度” 时，会从 “叶子节点高度为 1” 和 “叶子节点高度为 0” 两种常见定义入手，避免大家踩坑；统计 “叶子节点” 时，会拆解判断叶子节点的核心条件，再结合遍历逻辑实现计数；至于 “树的结构调整”，会通过具体例子展示交换左右子树的效果，甚至还会延伸到 “判断两棵树是否相同” 的逻辑 —— 毕竟只有先理解 “相同” 的定义，才能更好地处理 “调整” 的需求。

我知道，对于刚掌握遍历的大家来说，这些进阶操作可能会有一些挑战，比如计算树的高度时需要理解 “递归的返回值传递”，统计叶子节点时需要注意 “递归终止条件的边界处理”。但请相信，这些操作的核心逻辑依然离不开 “分治思想”—— 把 “操作整棵树” 拆成 “操作左子树 + 操作右子树 + 处理当前节点”，和我们之前学的遍历逻辑是一脉相承的。只要大家跟着我的节奏，一步步拆解原理、分析代码、验证效果，就能慢慢打通这些操作之间的关联，最终构建起一套完整的链式二叉树 “技能树”。

那么，接下来就让我们带着上一篇的基础，开启链式二叉树进阶操作的探索之旅吧！相信这一次的学习，会让大家对链式二叉树的理解更上一层楼，以后再面对与二叉树相关的问题时，不仅能想到 “用遍历解决”，更能灵活运用各种进阶操作，真正做到 “游刃有余” 地驾驭链式二叉树！

统计二叉树结点个数：

那么首当其冲的就是，我们要如何去统计一棵二叉树的节点个数，我们依旧是以这棵树作为例子：

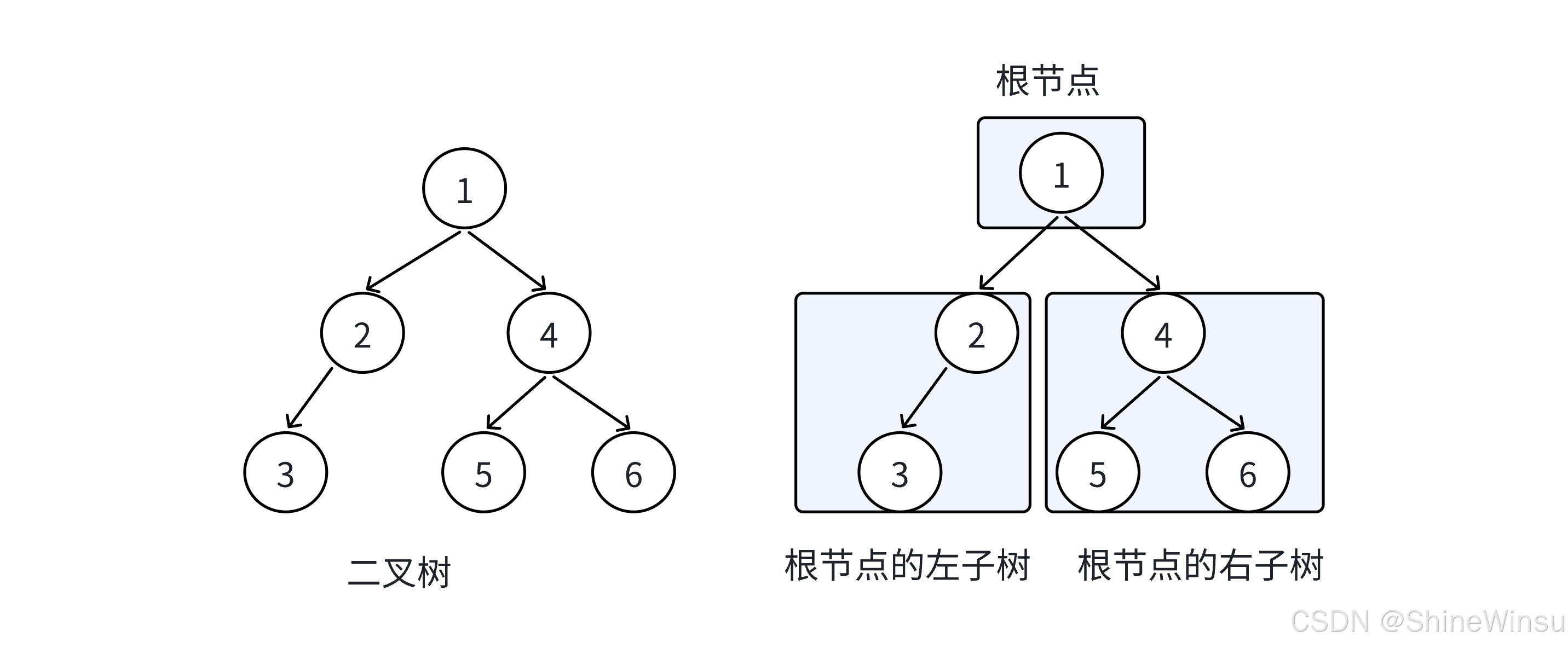
可以看到，这棵二叉树一共有6个节点，那么，我们要怎么进行统计呢？

首先，我们需要明确，我们依旧是需要使用递归，去将一棵二叉树拆分为根节点，左子树，右子树的问题。

而且，我们本质上还是需要我们上篇博客中所提到的后序遍历，只不过稍微有些变化罢了。

那么呢，我们的递归返回条件，依旧得是碰到NULL就返回0，因为我们要求函数返回类型要是整型，那么然后呢？我们要怎么操作呢？

其实很简单，因为我们知道，统计一棵二叉树的节点个数，其实本质上就是统计一棵二叉树的根节点个数罢了，那么，我们是不是可以，先去走左子树，走完某个根节点的左子树之后，暂时忽略那一个根节点，去走它的右子树，走完右子树后，我们再去访问这个根节点，同时执行加一，这个加一是指这个根节点，表示这里有一个根节点。

大家要把上面这段话仔细理解理解，并结合着图去进行分析，本质是不难的，但是也有需要着重注意的点，那就是由于这是统计数据，并不是打印数据，所以我们不能类似后序遍历一样，去走了左子树，再走了右子树后，去表达数据，因为我们去return，只是return某个值，并不能进行累加，所以即使统计了有很多个节点，函数也依然只是返回一个1，不会去进行累加，所以，我们得直接返回遍历完某个根节点的左右子树后再加一，或者返回1的时候，后面调用递归的返回得是递归左右子树的相加，这么一来，才能实现累加，可千万不能直接返回1，而不进行相加的操作。

其实统计节点个数和遍历的核心逻辑很像，都是用递归把 "统计整棵树" 拆成 "统计子树" 的小问题，关键思路就是：整棵树的节点个数 = 左子树的节点个数 + 右子树的节点个数 + 1（当前根节点自己）。刚开始可能会有点绕，但跟着例子一步步走，你会发现：哦，原来和遍历的逻辑是通的，只是把 "访问节点" 换成了 "统计节点并累加" 而已！

我们还是以之前的二叉树（根节点为 1，左子树以 2 为根，右子树以 4 为根）为例，先把树的结构再明确一下，方便后续对照：

        1        （根节点）/ \2   4      （第2层）/   / \3   5   6    （第3层）

接下来，咱们从 "执行步骤"" 生活化例子 ""代码实现"" 递归栈帧细节 " 四个部分，把统计二叉树节点个数彻底讲透。

一、统计节点个数的执行步骤（核心：左子树节点数 + 右子树节点数 + 1）

统计二叉树节点个数的规则是：如果当前节点为空，返回 0（没有节点）；否则，返回左子树的节点个数 + 右子树的节点个数 + 1（当前根节点自己）。而且对左、右子树的统计，也完全遵循这个规则，直到遇到空节点才停止。

咱们一步一步拆解整个过程：

步骤 1：从整棵树的根节点 1 开始，统计其节点个数

因为根节点 1 不为空，所以需要统计左子树（以 2 为根的子树）的节点个数、右子树（以 4 为根的子树）的节点个数，然后相加再 +1（根节点 1 自己）。

子步骤 1.1：统计节点 2 所在左子树的节点个数

节点 2 不为空，所以需要统计它的左子树（以 3 为根的子树）的节点个数、右子树（空）的节点个数，然后相加再 +1（节点 2 自己）。

子步骤 1.1.1：统计节点 3 所在左子树的节点个数

节点 3 不为空，统计它的左子树（空）的节点个数（返回 0）、右子树（空）的节点个数（返回 0），相加再 +1（节点 3 自己），结果为 0 + 0 + 1 = 1。所以节点 3 所在子树的节点个数是 1。

子步骤 1.1.2：节点 2 的右子树为空，返回 0。所以节点 2 所在子树的节点个数是 1（左子树节点数） + 0（右子树节点数） + 1（节点 2 自己） = 2。

步骤 2：统计节点 1 的右子树（以 4 为根的子树）的节点个数

节点 4 不为空，统计它的左子树（以 5 为根的子树）的节点个数、右子树（以 6 为根的子树）的节点个数，然后相加再 +1（节点 4 自己）。

子步骤 2.1：统计节点 5 所在左子树的节点个数

节点 5 不为空，其左子树和右子树都为空，所以节点 5 所在子树的节点个数是 0 + 0 + 1 = 1。

子步骤 2.2：统计节点 6 所在右子树的节点个数

节点 6 不为空，其左子树和右子树都为空，所以节点 6 所在子树的节点个数是 0 + 0 + 1 = 1。

所以节点 4 所在子树的节点个数是 1（左子树节点数） + 1（右子树节点数） + 1（节点 4 自己） = 3。

步骤 3：整棵树的节点个数

整棵树的节点个数是 2（左子树节点数） + 3（右子树节点数） + 1（根节点 1 自己） = 6，与我们手动数的结果一致。

二、生活化例子："公司组织架构人数统计"

把二叉树想象成一个公司的组织架构，根节点是 CEO，左子树是技术部门，右子树是业务部门。每个部门又可以分成更小的团队（子树）。统计公司总人数，就需要统计技术部门人数、业务部门人数，然后加上 CEO（1 人）。

1. 节点对应的公司职位明确

• 根节点 1：CEO（负责整个公司）
• 左子树根 2：技术总监（管理技术部门）
• 左子树的左子树 3：开发团队组长（管理开发团队）
• 右子树根 4：业务总监（管理业务部门）
• 右子树的左子树 5：销售团队组长（管理销售团队）
• 右子树的右子树 6：市场团队组长（管理市场团队）

2. 统计人数的流程

第一步：统计技术部门人数

HR 说："先统计技术部门的人数，技术部门由技术总监 2 管理。"技术总监 2 说："我管理的技术部门又分成了开发团队，由组长 3 管理，我自己也算 1 人，我的右方没有其他技术团队了。"开发团队组长 3 说："我管理的开发团队没有再分组了，我自己算 1 人。" 所以开发团队人数是 1，技术部门总人数是 1（开发团队） + 0（无其他团队） + 1（技术总监 2 自己） = 2。

第二步：统计业务部门人数

HR 接着说："再统计业务部门的人数，业务部门由业务总监 4 管理。"业务总监 4 说："我管理的业务部门分成了销售团队和市场团队，分别由组长 5 和组长 6 管理，我自己也算 1 人。"销售团队组长 5 说："我管理的销售团队没有再分组，我自己算 1 人。"市场团队组长 6 说："我管理的市场团队没有再分组，我自己算 1 人。" 所以业务部门人数是 1（销售团队） + 1（市场团队） + 1（业务总监 4 自己） = 3。

第三步：统计公司总人数

HR 最后说："公司总人数是技术部门人数 + 业务部门人数 + CEO（1 人）。" 即 2 + 3 + 1 = 6 人，和实际数的一致。

3. 统计节点个数的本质："分治累加"

从公司人数统计的例子能看出来，统计节点个数的逻辑是 "分而治之，累加求和"。把大的统计问题（整棵树的节点数）分解成小的统计问题（左、右子树的节点数），然后将子问题的结果累加，再加上当前节点的 1 个，就得到了当前树的节点总数。这种思想在很多算法问题中都有应用，比如计算树的高度、求树中某类节点的数量等。

三、统计节点个数的递归代码实现

统计节点个数的代码逻辑清晰，基于 "左子树节点数 + 右子树节点数 + 1（当前节点）" 的规则。咱们直接上代码，关键地方加了注释：

// 1. 先定义二叉树节点结构体（和之前一致）
typedef struct BinaryTreeNode {int data;                       // 节点存储的数据struct BinaryTreeNode* left;    // 指向左子节点的指针struct BinaryTreeNode* right;   // 指向右子节点的指针
} btn;  // 结构体别名，简化后续使用// 2. 统计节点个数的函数：参数是当前子树的根节点，返回该子树的节点个数
int countNodes(btn* root) {// 递归终止条件：如果当前节点是空，返回 0（没有节点）if (root == NULL) {return 0;}// 核心逻辑：当前树的节点个数 = 左子树节点个数 + 右子树节点个数 + 1（当前根节点）int leftCount = countNodes(root->left);   // 统计左子树的节点个数int rightCount = countNodes(root->right); // 统计右子树的节点个数return leftCount + rightCount + 1;        // 返回总数
}

代码的核心就是递归地统计左、右子树的节点数，然后相加再加上当前节点的 1 个。比如咱们的示例树，调用 countNodes(root)（root 指向节点 1），最终会返回 6，和我们手动计算的结果一致。

四、统计节点个数的递归栈帧细节（彻底理解 "怎么跑的"）

为了彻底理解递归统计节点个数的过程，我们还是以 countNodes(root)（root 指向节点 1）为例，拆解每一步的栈状态、执行操作和返回结果。

核心概念：函数调用栈

递归的时候，每次调用 countNodes 函数，系统都会在 "函数栈" 里新增一个 "栈帧"—— 这个栈帧记录着当前函数的参数（比如 root 指向哪个节点）、局部变量（leftCount、rightCount）以及 "下一步要执行的代码位置"（断点）。当函数执行到 return，这张 "便签" 就会被撕掉（栈帧弹出），程序回到上一张便签的 "断点位置" 继续执行。

1. 初始调用：countNodes(1)（根节点 1）

• 栈状态（从上到下是最近调用的函数，栈帧里记录 "函数名 + root 值 + 断点"）：[countNodes(1)：root=1，断点在"计算 leftCount 后"]
• 执行步骤：
  1. 检查 root=1 不为空，不触发终止条件。
  2. 执行 "统计左子树节点个数"→ 调用 countNodes(root->left)，也就是 countNodes(2)（节点 1 的左子树是 2）。
  3. 栈帧变化：把 countNodes(1) 的栈帧暂停（断点记在 " 计算完 countNodes(2) 后，要计算 rightCount"），新增 countNodes(2) 的栈帧压入栈。此时栈状态：[countNodes(1)（暂停）, countNodes(2)：root=2，断点在"计算 leftCount 后"]。
• 当前返回结果：无（还没到返回步骤）。

2. 执行 countNodes(2)（节点 2，节点 1 的左子树）

• 栈状态：[countNodes(1)（暂停）, countNodes(2)：root=2，断点在"计算 leftCount 后"]
• 执行步骤：
  1. 检查 root=2 不为空，不触发终止条件。
  2. 执行 "统计左子树节点个数"→ 调用 countNodes(root->left)，也就是 countNodes(3)（节点 2 的左子树是 3）。
  3. 栈帧变化：暂停 countNodes(2)（断点记在 " 计算完 countNodes(3) 后，要计算 rightCount"），新增 countNodes(3) 的栈帧压入栈。此时栈状态：[countNodes(1)（暂停）, countNodes(2)（暂停）, countNodes(3)：root=3，断点在"计算 leftCount 后"]。
• 当前返回结果：无。

3. 执行 countNodes(3)（节点 3，节点 2 的左子树）

• 栈状态：[countNodes(1)（暂停）, countNodes(2)（暂停）, countNodes(3)：root=3，断点在"计算 leftCount 后"]
• 执行步骤：
  1. 检查 root=3 不为空，不触发终止条件。
  2. 执行 "统计左子树节点个数"→ 调用 countNodes(root->left)，也就是 countNodes(NULL)（节点 3 的左子树是空）。
  3. 栈帧变化：暂停 countNodes(3)（断点记在 " 计算完 countNodes(NULL) 后，要计算 rightCount"），新增 countNodes(NULL) 的栈帧压入栈。此时栈状态：[countNodes(1)（暂停）, countNodes(2)（暂停）, countNodes(3)（暂停）, countNodes(NULL)：root=NULL]。
• 当前返回结果：无。

4. 执行 countNodes(NULL)（节点 3 的左子树）

• 栈状态：[countNodes(1)（暂停）, countNodes(2)（暂停）, countNodes(3)（暂停）, countNodes(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发终止条件，返回 0。
  2. 执行 return，撕掉 countNodes(NULL) 的栈帧（弹出栈），回到 countNodes(3) 的 "断点位置"—— 也就是 " 计算完 countNodes(left) 后，准备计算 rightCount"。
• 当前返回结果：0（leftCount = 0）。

5. 回到 countNodes(3)，继续执行

• 栈状态：[countNodes(1)（暂停）, countNodes(2)（暂停）, countNodes(3)：root=3，断点在"计算 leftCount 后"]
• 执行步骤：
  1. 执行 "统计右子树节点个数"→ 调用 countNodes(root->right)，也就是 countNodes(NULL)（节点 3 的右子树是空）。
  2. 栈帧变化：暂停 countNodes(3)（断点记在 " 计算完 countNodes(NULL) 后，要返回结果 "），新增 countNodes(NULL) 的栈帧压入栈。此时栈状态：[countNodes(1)（暂停）, countNodes(2)（暂停）, countNodes(3)（暂停）, countNodes(NULL)：root=NULL]。
• 当前返回结果：0（leftCount = 0）。

6. 再执行 countNodes(NULL)（节点 3 的右子树）

• 栈状态：[countNodes(1)（暂停）, countNodes(2)（暂停）, countNodes(3)（暂停）, countNodes(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发终止条件，返回 0。
  2. 执行 return，撕掉 countNodes(NULL) 的栈帧（弹出栈），回到 countNodes(3) 的 "断点位置"—— 也就是 " 计算完 countNodes(right) 后，准备返回结果 "。
  3. countNodes(3) 的 leftCount = 0，rightCount = 0，所以返回 0 + 0 + 1 = 1。
  4. 执行 return，撕掉 countNodes(3) 的栈帧（弹出栈），回到 countNodes(2) 的 "断点位置"—— 也就是 " 计算完 countNodes(left) 后，准备计算 rightCount"。
• 当前返回结果：1（leftCount = 1）。

7. 回到 countNodes(2)，继续执行

• 栈状态：[countNodes(1)（暂停）, countNodes(2)：root=2，断点在"计算 leftCount 后"]
• 执行步骤：
  1. 执行 "统计右子树节点个数"→ 调用 countNodes(root->right)，也就是 countNodes(NULL)（节点 2 的右子树是空）。
  2. 栈帧变化：暂停 countNodes(2)（断点记在 " 计算完 countNodes(NULL) 后，要返回结果 "），新增 countNodes(NULL) 的栈帧压入栈。此时栈状态：[countNodes(1)（暂停）, countNodes(2)（暂停）, countNodes(NULL)：root=NULL]。
• 当前返回结果：1（leftCount = 1）。

8. 执行 countNodes(NULL)（节点 2 的右子树）

• 栈状态：[countNodes(1)（暂停）, countNodes(2)（暂停）, countNodes(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发终止条件，返回 0。
  2. 执行 return，撕掉 countNodes(NULL) 的栈帧（弹出栈），回到 countNodes(2) 的 "断点位置"—— 也就是 " 计算完 countNodes(right) 后，准备返回结果 "。
  3. countNodes(2) 的 leftCount = 1，rightCount = 0，所以返回 1 + 0 + 1 = 2。
  4. 执行 return，撕掉 countNodes(2) 的栈帧（弹出栈），回到 countNodes(1) 的 "断点位置"—— 也就是 " 计算完 countNodes(left) 后，准备计算 rightCount"。
• 当前返回结果：2（leftCount = 2）。

9. 回到 countNodes(1)，继续执行

• 栈状态：[countNodes(1)：root=1，断点在"计算 leftCount 后"]
• 执行步骤：
  1. 执行 "统计右子树节点个数"→ 调用 countNodes(root->right)，也就是 countNodes(4)（节点 1 的右子树是 4）。
  2. 栈帧变化：暂停 countNodes(1)（断点记在 " 计算完 countNodes(4) 后，要返回结果 "），新增 countNodes(4) 的栈帧压入栈。此时栈状态：[countNodes(1)（暂停）, countNodes(4)：root=4，断点在"计算 leftCount 后"]。
• 当前返回结果：2（leftCount = 2）。

10. 执行 countNodes(4)（节点 4，节点 1 的右子树）

• 栈状态：[countNodes(1)（暂停）, countNodes(4)：root=4，断点在"计算 leftCount 后"]
• 执行步骤：
  1. 检查 root=4 不为空，不触发终止条件。
  2. 执行 "统计左子树节点个数"→ 调用 countNodes(root->left)，也就是 countNodes(5)（节点 4 的左子树是 5）。
  3. 栈帧变化：暂停 countNodes(4)（断点记在 " 计算完 countNodes(5) 后，要计算 rightCount"），新增 countNodes(5) 的栈帧压入栈。此时栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(5)：root=5，断点在"计算 leftCount 后"]。
• 当前返回结果：2（leftCount = 2）。

11. 执行 countNodes(5)（节点 5，节点 4 的左子树）

• 栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(5)：root=5，断点在"计算 leftCount 后"]
• 执行步骤：
  1. 检查 root=5 不为空，不触发终止条件。
  2. 执行 "统计左子树节点个数"→ 调用 countNodes(root->left)，也就是 countNodes(NULL)（节点 5 的左子树是空）。
  3. 栈帧变化：暂停 countNodes(5)（断点记在 " 计算完 countNodes(NULL) 后，要计算 rightCount"），新增 countNodes(NULL) 的栈帧压入栈。此时栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(5)（暂停）, countNodes(NULL)：root=NULL]。
• 当前返回结果：2（leftCount = 2）。

12. 执行 countNodes(NULL)（节点 5 的左子树）

• 栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(5)（暂停）, countNodes(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发终止条件，返回 0。
  2. 执行 return，撕掉 countNodes(NULL) 的栈帧（弹出栈），回到 countNodes(5) 的 "断点位置"—— 也就是 " 计算完 countNodes(left) 后，准备计算 rightCount"。
• 当前返回结果：0（leftCount = 0）。

13. 回到 countNodes(5)，继续执行

• 栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(5)：root=5，断点在"计算 leftCount 后"]
• 执行步骤：
  1. 执行 "统计右子树节点个数"→ 调用 countNodes(root->right)，也就是 countNodes(NULL)（节点 5 的右子树是空）。
  2. 栈帧变化：暂停 countNodes(5)（断点记在 " 计算完 countNodes(NULL) 后，要返回结果 "），新增 countNodes(NULL) 的栈帧压入栈。此时栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(5)（暂停）, countNodes(NULL)：root=NULL]。
• 当前返回结果：0（leftCount = 0）。

14. 再执行 countNodes(NULL)（节点 5 的右子树）

• 栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(5)（暂停）, countNodes(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发终止条件，返回 0。
  2. 执行 return，撕掉 countNodes(NULL) 的栈帧（弹出栈），回到 countNodes(5) 的 "断点位置"—— 也就是 " 计算完 countNodes(right) 后，准备返回结果 "。
  3. countNodes(5) 的 leftCount = 0，rightCount = 0，所以返回 0 + 0 + 1 = 1。
  4. 执行 return，撕掉 countNodes(5) 的栈帧（弹出栈），回到 countNodes(4) 的 "断点位置"—— 也就是 " 计算完 countNodes(left) 后，准备计算 rightCount"。
• 当前返回结果：1（leftCount = 1）。

15. 回到 countNodes(4)，继续执行

• 栈状态：[countNodes(1)（暂停）, countNodes(4)：root=4，断点在"计算 leftCount 后"]
• 执行步骤：
  1. 执行 "统计右子树节点个数"→ 调用 countNodes(root->right)，也就是 countNodes(6)（节点 4 的右子树是 6）。
  2. 栈帧变化：暂停 countNodes(4)（断点记在 " 计算完 countNodes(6) 后，要返回结果 "），新增 countNodes(6) 的栈帧压入栈。此时栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(6)：root=6，断点在"计算 leftCount 后"]。
• 当前返回结果：1（leftCount = 1）。

16. 执行 countNodes(6)（节点 6，节点 4 的右子树）

• 栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(6)：root=6，断点在"计算 leftCount 后"]
• 执行步骤：
  1. 检查 root=6 不为空，不触发终止条件。
  2. 执行 "统计左子树节点个数"→ 调用 countNodes(root->left)，也就是 countNodes(NULL)（节点 6 的左子树是空）。
  3. 栈帧变化：暂停 countNodes(6)（断点记在 " 计算完 countNodes(NULL) 后，要计算 rightCount"），新增 countNodes(NULL) 的栈帧压入栈。此时栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(6)（暂停）, countNodes(NULL)：root=NULL]。
• 当前返回结果：1（leftCount = 1）。

17. 执行 countNodes(NULL)（节点 6 的左子树）

• 栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(6)（暂停）, countNodes(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发终止条件，返回 0。
  2. 执行 return，撕掉 countNodes(NULL) 的栈帧（弹出栈），回到 countNodes(6) 的 "断点位置"—— 也就是 " 计算完 countNodes(left) 后，准备计算 rightCount"。
• 当前返回结果：0（leftCount = 0）。

18. 回到 countNodes(6)，继续执行

• 栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(6)：root=6，断点在"计算 leftCount 后"]
• 执行步骤：
  1. 执行 "统计右子树节点个数"→ 调用 countNodes(root->right)，也就是 countNodes(NULL)（节点 6 的右子树是空）。
  2. 栈帧变化：暂停 countNodes(6)（断点记在 " 计算完 countNodes(NULL) 后，要返回结果 "），新增 countNodes(NULL) 的栈帧压入栈。此时栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(6)（暂停）, countNodes(NULL)：root=NULL]。
• 当前返回结果：0（leftCount = 0）。

19. 再执行 countNodes(NULL)（节点 6 的右子树）

• 栈状态：[countNodes(1)（暂停）, countNodes(4)（暂停）, countNodes(6)（暂停）, countNodes(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发终止条件，返回 0。
  2. 执行 return，撕掉 countNodes(NULL) 的栈帧（弹出栈），回到 countNodes(6) 的 "断点位置"—— 也就是 " 计算完 countNodes(right) 后，准备返回结果 "。
  3. countNodes(6) 的 leftCount = 0，rightCount = 0，所以返回 0 + 0 + 1 = 1。
  4. 执行 return，撕掉 countNodes(6) 的栈帧（弹出栈），回到 countNodes(4) 的 "断点位置"—— 也就是 " 计算完 countNodes(right) 后，准备返回结果 "。
• 当前返回结果：1（rightCount = 1）。

20. 回到 countNodes(4)，继续执行

• 栈状态：[countNodes(1)（暂停）, countNodes(4)：root=4，断点在"计算 rightCount 后"]
• 执行步骤：
  1. countNodes(4) 的 leftCount = 1，rightCount = 1，所以返回 1 + 1 + 1 = 3。
  2. 执行 return，撕掉 countNodes(4) 的栈帧（弹出栈），回到 countNodes(1) 的 "断点位置"—— 也就是 " 计算完 countNodes(right) 后，准备返回结果 "。
• 当前返回结果：3（rightCount = 3）。

21. 回到 countNodes(1)，继续执行

• 栈状态：[countNodes(1)：root=1，断点在"计算 rightCount 后"]
• 执行步骤：
  1. countNodes(1) 的 leftCount = 2，rightCount = 3，所以返回 2 + 3 + 1 = 6。
  2. 执行 return，撕掉 countNodes(1) 的栈帧（弹出栈）。
• 当前返回结果：6。

22. 统计节点个数结束

• 栈状态：空（所有栈帧都已弹出）
• 最终返回结果：6
• 核心统计逻辑：整棵树的节点个数 = 左子树节点数（2） + 右子树节点数（3） + 1（根节点） = 6

五、总结：统计节点个数的核心要点

通过上面的详细拆解，我们可以总结出统计二叉树节点个数的几个核心要点：

1. 统计逻辑：严格遵循 "左子树节点数 + 右子树节点数 + 1（当前节点）"，这是递归统计的核心公式。
2. 递归本质：利用二叉树的递归结构，将 "统计整棵树" 拆成 "统计左子树 + 统计右子树 + 加 1"，子树的统计逻辑与整棵树完全一致。
3. 终止条件：遇到空节点（NULL）时返回 0，这是递归能正常结束的关键，避免无限循环。
4. 栈的作用：递归调用时，函数栈自动记录 "未完成的父节点计算"，确保左、右子树都统计完后能回到父节点，继续累加计算。
5. 时间复杂度：O (n)，其中 n 是树的节点个数，因为每个节点都会被访问并统计一次。
6. 空间复杂度：O (h)，其中 h 是树的高度，主要是递归调用栈的空间开销。在最坏情况下（单链树），h = n，空间复杂度为 O (n)；在最好情况下（完全二叉树），h = log n，空间复杂度为 O (log n)。

掌握了统计节点个数的方法，你会发现它和遍历的逻辑是相通的 —— 都是 "递归拆解 + 栈帧管理"，区别只是把 "访问节点" 换成了 "统计节点并累加"。这种 "统一逻辑 + 微小差异" 的特点，正是二叉树操作的精髓所在。记住：统计节点个数的核心就是 "左子树节点数 + 右子树节点数 + 1"，这是解决很多二叉树问题的基础。

下面是完整代码：；

//求出二叉树的节点个数
int binarytreesize(btn* root)
{//如果节点为NULL，就代表这里没有节点if (root == NULL){return 0;}//如果节点不为空，就代表这里有节点，即它是根节点，有左右子树//那么我对于这个节点，就得返回它的左右子树的节点的数量//同时也得加1，因为以防该根节点的两个子树都是NULL，//那么+1就代表算上这个根节点的数量//使用递归，一路判断下去,所有的根节点//直到遇到NULL，开始返回//我们这里直接返回，是因为我们是从最上面的根节点开始的//所以对于最上面的根节点而言，它的左右子树节点个数//再加一（即根节点本身），不就是二叉树的所有节点数量了吗//类似后序遍历，先左子树，再右子树，最后根节点return binarytreesize(root->left) + binarytreesize(root->right) + 1;
}

我觉得大家要理解，就必须要结合着上面所说的例子进行详细理解。

下面给上我的手写解析：

其实本质上还是不难的。

统计二叉树的叶子节点个数：

其实这一个功能，和我们统计二叉树节点个数是很类似的，只不过还是有所不同的，不同点就在于，我们上面的统计二叉树节点个数是只要你是个根节点，即只要你不为空，你就得被统计进去，而对于叶子节点的个数的话，可就不是只要你不为空，你就得被统计进去了。

我们先来了解一下，什么是叶子节点：

在树（包括二叉树、多叉树等各种树结构）的相关概念里，叶子节点（也叫叶节点）是一个基础且重要的定义，我们可以从以下几个方面详细理解：

1. 核心定义

叶子节点是树中没有子节点的节点，也就是节点的 “度” 为 0（“度” 指的是一个节点拥有的子节点的数量）。

2. 结合树的结构理解

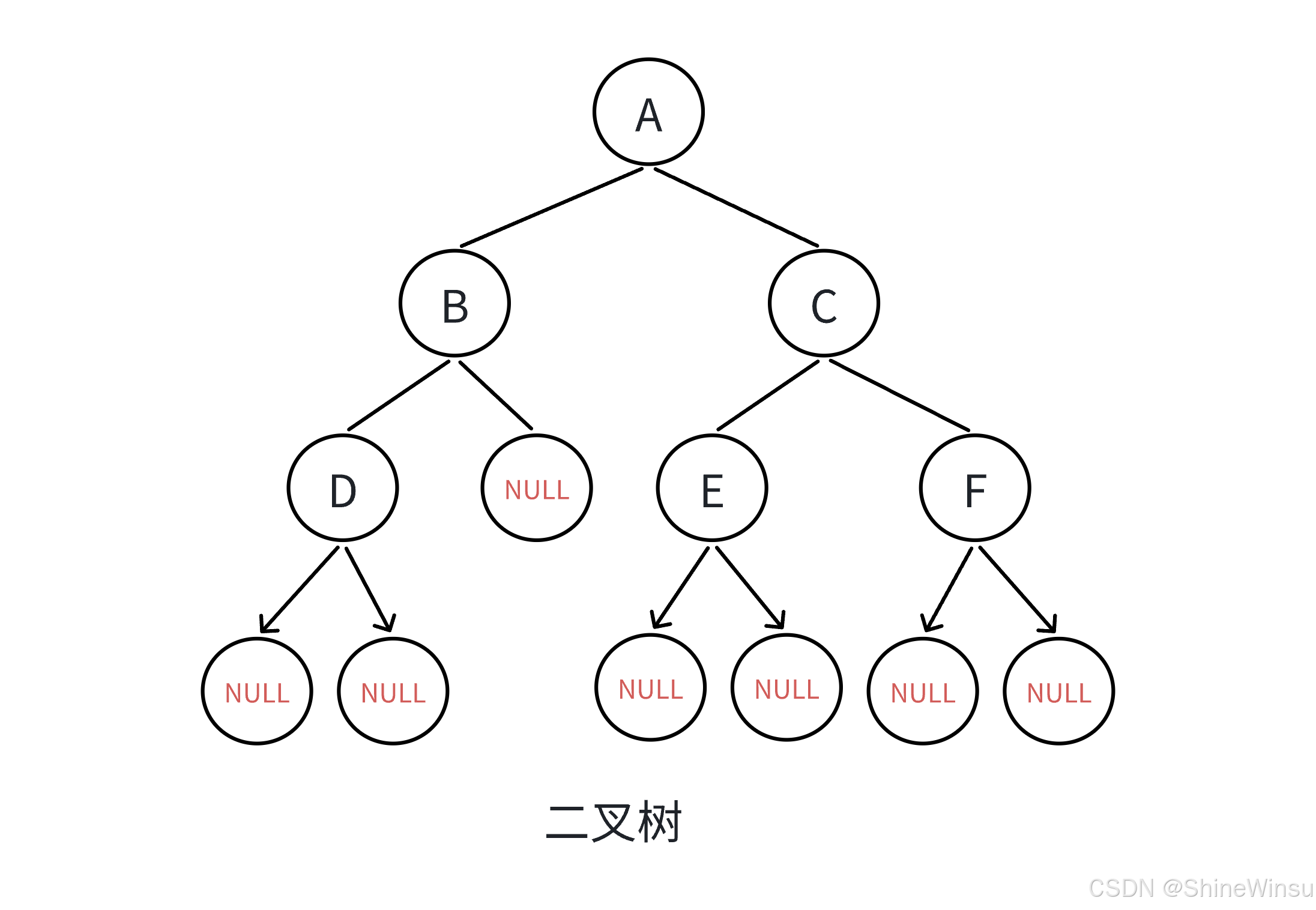
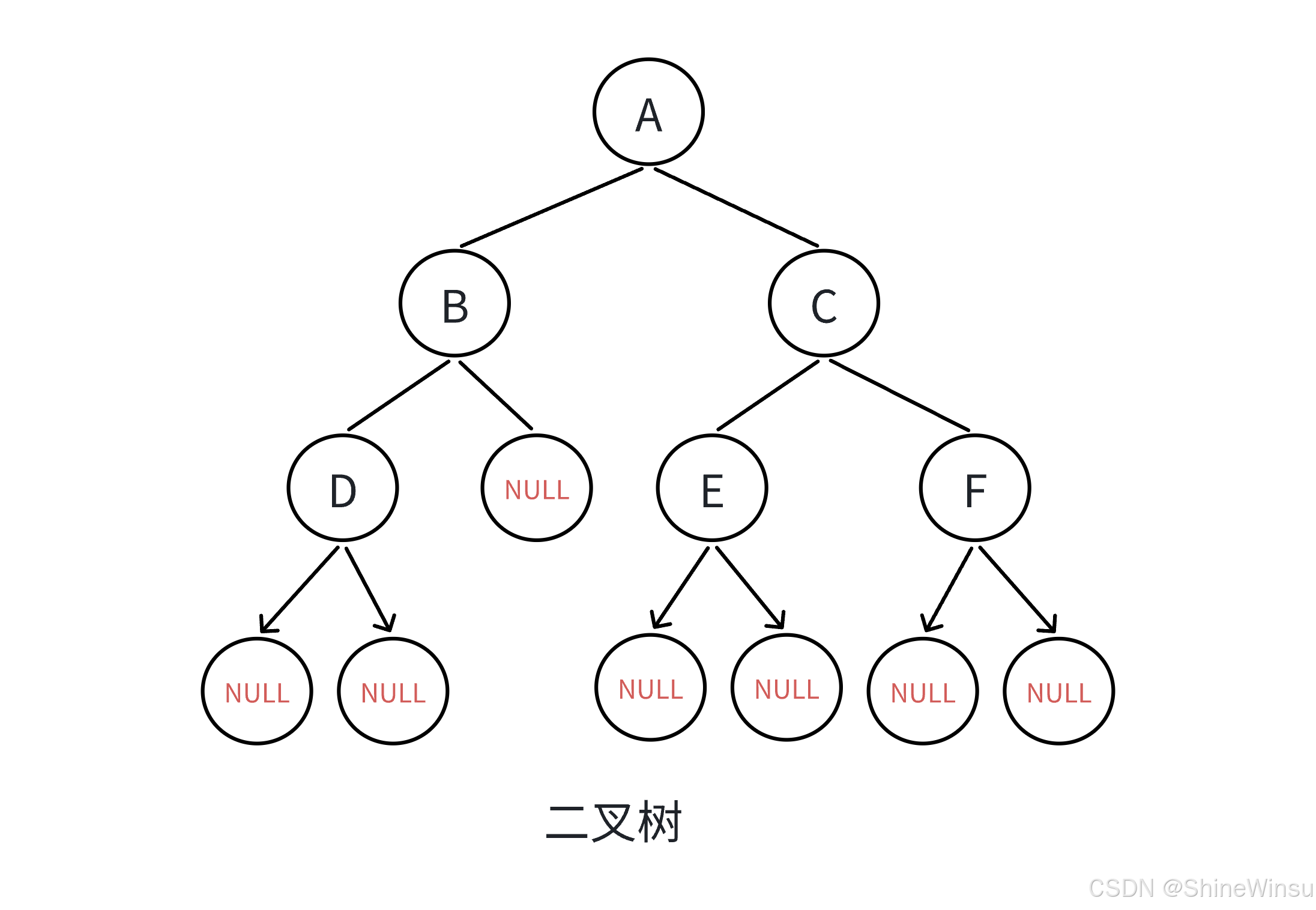
以二叉树为例，来看一个具体的树结构：

        A        （根节点，度为2，有2个子节点B、C）/ \B   C      （B的度为2，有子节点D、E；C的度为1，有子节点F）/ \   \D   E   F    （D的度为0，无子女；E的度为0，无子女；F的度为0，无子女）

在这个二叉树中：

• 根节点 A 有子节点 B 和 C，所以它不是叶子节点（度为 2）。
• 节点 B 有子节点 D 和 E，不是叶子节点（度为 2）；节点 C 有子节点 F，不是叶子节点（度为 1）。
• 节点 D、E、F 都没有子节点，所以它们都是叶子节点（度为 0）。

3. 与其他节点的对比

树中的节点除了叶子节点，还有 “分支节点”（也叫内部节点）。分支节点是有子节点的节点（度 ≥ 1），比如上面例子中的 A、B、C 都是分支节点。

4. 叶子节点的特点

• 位置特点：通常位于树的 “最底层”（但不是绝对的，比如如果树只有一个节点，这个节点既是根节点也是叶子节点）。
• 数量影响：叶子节点的数量会影响树的一些性质，比如在二叉树中，若叶子节点数为 n0​，度为 2 的节点数为 n2​，则有 n0​=n2​+1（这是二叉树的一个重要性质）。
• 作用：在很多树的应用场景中，叶子节点往往存储着最终的数据或结果，比如在 “决策树” 中，叶子节点代表最终的决策结果；在 “文件系统的目录树” 中，叶子节点可能代表具体的文件（而目录是分支节点）。

简单来说，叶子节点就是树里 “没有孩子” 的节点，是树结构的 “末端节点”。

我总结一下，其实叶子节点就是二叉树中左右孩子都是NULL的根节点啦

那么，这个和我们上面的统计二叉树节点个数有什么联系，又有什么不同呢？

其实呢，首先依旧是用后序遍历，（当然，什么遍历都行，但是后序遍历会更好理解且好用一些），如何呢，我们递归的返回条件依旧得是碰到NULL就返回，注意，要返回0，毕竟我们已经要求了函数返回类型是整型。

然后呢，我要像什上面统计节点个数一样直接进行加吗，肯定不是的，因为我们的叶子节点不完全等于根节点，所以，为了能够单独找到叶子结点，我们就得用条件判断，当某个根节点能符合叶子节点的特征之后，我们再return 1，此时就代表记录了这个根节点，在这里存储了1，后面我再return递归左子树+递归右子树，此时就能记录二叉树中叶子节点的个数了。

统计叶子节点个数和统计总节点个数的核心逻辑很像，都是用递归把 "统计整棵树" 拆成 "统计子树" 的小问题，但关键区别在于：只有当节点是叶子节点时才计数，非叶子节点只负责汇总左右子树的结果。刚开始可能会有点绕，但跟着例子一步步走，你会发现：哦，原来和统计总节点数的逻辑是通的，只是把 "每个节点都计数" 换成了 "只有叶子节点才计数" 而已！

我们还是以之前的二叉树（根节点为 1，左子树以 2 为根，右子树以 4 为根）为例，先把树的结构再明确一下，方便后续对照：

        1        （根节点，非叶子节点）/ \2   4      （第2层，都不是叶子节点）/   / \3   5   6    （第3层，都是叶子节点）

在这棵树中，叶子节点是 3、5、6（它们都没有子节点），所以叶子节点总数是 3。

接下来，咱们从 "执行步骤"" 生活化例子 ""代码实现"" 递归栈帧细节 " 四个部分，把统计叶子节点个数彻底讲透。

一、统计叶子节点个数的执行步骤（核心：只有叶子节点才计数）

统计叶子节点个数的规则是：

1. 如果当前节点为空，返回 0（没有节点，自然没有叶子节点）
2. 如果当前节点是叶子节点（左、右子树都为空），返回 1（这个节点本身就是叶子节点）
3. 否则，返回左子树的叶子节点个数 + 右子树的叶子节点个数（当前节点不是叶子，汇总子树的结果）

而且对左、右子树的统计，也完全遵循这个规则，直到遇到空节点或叶子节点才停止。

咱们一步一步拆解整个过程：

步骤 1：从整棵树的根节点 1 开始，判断它是否为叶子节点

节点 1 有左子树（节点 2）和右子树（节点 4），所以它不是叶子节点。按照规则 3，需要统计左子树（以 2 为根的子树）的叶子节点个数、右子树（以 4 为根的子树）的叶子节点个数，然后相加。

子步骤 1.1：统计节点 2 所在左子树的叶子节点个数

节点 2 有左子树（节点 3），所以它不是叶子节点。按照规则 3，需要统计它的左子树（以 3 为根的子树）的叶子节点个数、右子树（空）的叶子节点个数，然后相加。

子步骤 1.1.1：统计节点 3 所在左子树的叶子节点个数

节点 3 的左子树和右子树都为空，所以它是叶子节点。按照规则 2，返回 1。

子步骤 1.1.2：节点 2 的右子树为空，按照规则 1，返回 0。所以节点 2 所在子树的叶子节点个数是 1（左子树） + 0（右子树） = 1。

步骤 2：统计节点 1 的右子树（以 4 为根的子树）的叶子节点个数

节点 4 有左子树（节点 5）和右子树（节点 6），所以它不是叶子节点。按照规则 3，需要统计它的左子树（以 5 为根的子树）的叶子节点个数、右子树（以 6 为根的子树）的叶子节点个数，然后相加。

子步骤 2.1：统计节点 5 所在左子树的叶子节点个数

节点 5 的左子树和右子树都为空，所以它是叶子节点。按照规则 2，返回 1。

子步骤 2.2：统计节点 6 所在右子树的叶子节点个数

节点 6 的左子树和右子树都为空，所以它是叶子节点。按照规则 2，返回 1。

所以节点 4 所在子树的叶子节点个数是 1（左子树） + 1（右子树） = 2。

步骤 3：整棵树的叶子节点个数

整棵树的叶子节点个数是 1（左子树） + 2（右子树） = 3，与我们手动数的结果一致。

二、生活化例子："植物生长监测系统"

把二叉树想象成一棵果树的枝干结构，我们需要统计健康的叶子数量来评估树的生长状况。叶子节点就像是真正的树叶，只有当一个枝干末端没有再分叉时，才会长出叶子。

1. 节点对应的植物结构明确

• 根节点 1：树干（主茎，支撑整棵树）
• 左子树根 2：左主枝（从树干分出的主要枝条）
• 左子树的左子树 3：左末梢枝（左主枝末端的小枝条，长叶子）
• 右子树根 4：右主枝（从树干分出的主要枝条）
• 右子树的左子树 5：右主枝的左末梢枝（长叶子）
• 右子树的右子树 6：右主枝的右末梢枝（长叶子）

2. 统计叶子数量的流程（植物学家的工作）

第一步：检查左主枝的叶子数量

植物学家拿着记录本和放大镜，来到果园开始工作。他先从左边的主枝开始检查：

"让我看看这棵树的生长情况，先从左边的主枝开始。" 植物学家一边说着，一边仔细观察左主枝（节点 2）。

他发现左主枝还在继续分叉，没有直接长叶子，于是沿着枝条继续检查。走到左末梢枝（节点 3）时，他停下脚步，仔细观察："这个小枝条已经到末端了，没有再分叉，而且末端长着一片健康的叶子。"

植物学家在记录本上认真记录："左末梢枝：1 片叶子，叶片翠绿，无病虫害，生长状况良好。"

记录完毕后，他沿着原路返回，回到左主枝的位置。"左主枝的右边没有其他分支了，所以左主枝这一侧总共只有 1 片叶子。"

第二步：检查右主枝的叶子数量

完成左主枝的检查后，植物学家来到树的右侧，开始检查右主枝：

"现在看看右边的主枝，同样要仔细检查每个分支。" 他观察右主枝（节点 4），发现这个枝条也在继续分叉。

他先检查右边主枝的左侧分支，走到右主枝的左末梢枝（节点 5）："这个小枝条也到末端了，没有再分叉，末端有一片健康的叶子。" 他记录："右主枝左末梢：1 片叶子，叶片完整，光合作用活跃。"

回到右主枝后，他又检查右边的分支，来到右主枝的右末梢枝（节点 6）："这个小枝条同样是末端，没有分叉，有一片健康的叶子。" 他继续记录："右主枝右末梢：1 片叶子，叶片饱满，生长态势良好。"

"右主枝的两个分支各有 1 片叶子，所以右主枝这一侧总共有 2 片叶子。" 植物学家在记录本上汇总道。

第三步：统计整棵树的叶子总数

完成所有分支的检查后，植物学家回到树的根部，开始汇总数据：

"让我整理一下今天的检查结果：左主枝有 1 片叶子，右主枝有 2 片叶子，整棵树总共有 3 片叶子。"

他继续分析："从叶子的分布来看，这棵树的左右两侧生长相对均衡，所有叶子都很健康，没有发现病虫害。不过叶子总数偏少，可能需要加强施肥和浇水，促进更多新叶的生长。"

3. 统计叶子节点个数的本质："层层筛选，汇总末端"

从植物监测的例子能看出来，统计叶子节点个数的逻辑是 "只有末端的节点才是叶子，非末端节点只负责汇总"。就像植物的枝干，只有最末梢的小枝条才会长叶子，主枝和分枝只是支撑结构。这种 "筛选末端" 的思想在很多实际场景中都有应用，比如：

• 电路设计中的 "端点检测"
• 网络拓扑中的 "终端设备统计"
• 产品质量检验中的 "最终产品计数"

三、统计叶子节点个数的递归代码实现

统计叶子节点个数的代码逻辑清晰，基于 "空节点返回 0，叶子节点返回 1，非叶子节点返回左右子树之和" 的规则。咱们直接上代码，关键地方加了注释：

// 1. 先定义二叉树节点结构体（和之前一致）
typedef struct BinaryTreeNode {int data;                       // 节点存储的数据struct BinaryTreeNode* left;    // 指向左子节点的指针struct BinaryTreeNode* right;   // 指向右子节点的指针
} btn;  // 结构体别名，简化后续使用// 2. 统计叶子节点个数的函数：参数是当前子树的根节点，返回该子树的叶子节点个数
int countLeafNodes(btn* root) {// 规则1：如果当前节点是空，返回0（没有节点，自然没有叶子节点）if (root == NULL) {return 0;}// 规则2：如果当前节点是叶子节点（左、右子树都为空），返回1if (root->left == NULL && root->right == NULL) {return 1;}// 规则3：否则，返回左子树的叶子节点个数 + 右子树的叶子节点个数int leftLeafCount = countLeafNodes(root->left);   // 统计左子树的叶子节点个数int rightLeafCount = countLeafNodes(root->right); // 统计右子树的叶子节点个数return leftLeafCount + rightLeafCount;            // 返回总数
}

代码的核心就是三个判断条件，特别直观。比如咱们的示例树，调用 countLeafNodes(root)（root 指向节点 1），最终会返回 3，和我们手动计算的结果一致。

四、统计叶子节点个数的递归栈帧细节（彻底理解 "怎么跑的"）

为了彻底理解递归统计叶子节点个数的过程，我们还是以 countLeafNodes(root)（root 指向节点 1）为例，拆解每一步的栈状态、执行操作和返回结果。

核心概念：函数调用栈

递归的时候，每次调用 countLeafNodes 函数，系统都会在 "函数栈" 里新增一个 "栈帧"—— 这个栈帧记录着当前函数的参数（比如 root 指向哪个节点）、局部变量（leftLeafCount、rightLeafCount）以及 "下一步要执行的代码位置"（断点）。当函数执行到 return，这张 "便签" 就会被撕掉（栈帧弹出），程序回到上一张便签的 "断点位置" 继续执行。

1. 初始调用：countLeafNodes(1)（根节点 1）

• 栈状态（从上到下是最近调用的函数，栈帧里记录 "函数名 + root 值 + 断点"）：[countLeafNodes(1)：root=1，断点在"判断是否为叶子节点后"]
• 执行步骤：
  1. 检查 root=1 不为空，不触发规则 1。
  2. 检查 root=1 的左、右子树都不为空（有节点 2 和 4），所以不是叶子节点，不触发规则 2。
  3. 执行规则 3：统计左子树叶子节点个数→ 调用 countLeafNodes(root->left)，也就是 countLeafNodes(2)（节点 1 的左子树是 2）。
  4. 栈帧变化：把 countLeafNodes(1) 的栈帧暂停（断点记在 " 计算完 countLeafNodes(2) 后，要计算 rightLeafCount"），新增 countLeafNodes(2) 的栈帧压入栈。此时栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(2)：root=2，断点在"判断是否为叶子节点后"]。
• 当前返回结果：无（还没到返回步骤）。

2. 执行 countLeafNodes(2)（节点 2，节点 1 的左子树）

• 栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(2)：root=2，断点在"判断是否为叶子节点后"]
• 执行步骤：
  1. 检查 root=2 不为空，不触发规则 1。
  2. 检查 root=2 的左子树不为空（有节点 3），所以不是叶子节点，不触发规则 2。
  3. 执行规则 3：统计左子树叶子节点个数→ 调用 countLeafNodes(root->left)，也就是 countLeafNodes(3)（节点 2 的左子树是 3）。
  4. 栈帧变化：暂停 countLeafNodes(2)（断点记在 " 计算完 countLeafNodes(3) 后，要计算 rightLeafCount"），新增 countLeafNodes(3) 的栈帧压入栈。此时栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(2)（暂停）, countLeafNodes(3)：root=3，断点在"判断是否为叶子节点后"]。
• 当前返回结果：无。

3. 执行 countLeafNodes(3)（节点 3，节点 2 的左子树）

• 栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(2)（暂停）, countLeafNodes(3)：root=3，断点在"判断是否为叶子节点后"]
• 执行步骤：
  1. 检查 root=3 不为空，不触发规则 1。
  2. 检查 root=3 的左、右子树都为空，所以是叶子节点，触发规则 2，返回 1。
  3. 执行 return，撕掉 countLeafNodes(3) 的栈帧（弹出栈），回到 countLeafNodes(2) 的 "断点位置"—— 也就是 " 计算完 countLeafNodes(left) 后，准备计算 rightLeafCount"。
• 当前返回结果：1（leftLeafCount = 1）。

4. 回到 countLeafNodes(2)，继续执行

• 栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(2)：root=2，断点在"判断是否为叶子节点后"]
• 执行步骤：
  1. 执行规则 3：统计右子树叶子节点个数→ 调用 countLeafNodes(root->right)，也就是 countLeafNodes(NULL)（节点 2 的右子树是空）。
  2. 栈帧变化：暂停 countLeafNodes(2)（断点记在 " 计算完 countLeafNodes(NULL) 后，要返回结果 "），新增 countLeafNodes(NULL) 的栈帧压入栈。此时栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(2)（暂停）, countLeafNodes(NULL)：root=NULL]。
• 当前返回结果：1（leftLeafCount = 1）。

5. 执行 countLeafNodes(NULL)（节点 2 的右子树）

• 栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(2)（暂停）, countLeafNodes(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发规则 1，返回 0。
  2. 执行 return，撕掉 countLeafNodes(NULL) 的栈帧（弹出栈），回到 countLeafNodes(2) 的 "断点位置"—— 也就是 " 计算完 countLeafNodes(right) 后，准备返回结果 "。
  3. countLeafNodes(2) 的 leftLeafCount = 1，rightLeafCount = 0，所以返回 1 + 0 = 1。
  4. 执行 return，撕掉 countLeafNodes(2) 的栈帧（弹出栈），回到 countLeafNodes(1) 的 "断点位置"—— 也就是 " 计算完 countLeafNodes(left) 后，准备计算 rightLeafCount"。
• 当前返回结果：1（leftLeafCount = 1）。

6. 回到 countLeafNodes(1)，继续执行

• 栈状态：[countLeafNodes(1)：root=1，断点在"判断是否为叶子节点后"]
• 执行步骤：
  1. 执行规则 3：统计右子树叶子节点个数→ 调用 countLeafNodes(root->right)，也就是 countLeafNodes(4)（节点 1 的右子树是 4）。
  2. 栈帧变化：暂停 countLeafNodes(1)（断点记在 " 计算完 countLeafNodes(4) 后，要返回结果 "），新增 countLeafNodes(4) 的栈帧压入栈。此时栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(4)：root=4，断点在"判断是否为叶子节点后"]。
• 当前返回结果：1（leftLeafCount = 1）。

7. 执行 countLeafNodes(4)（节点 4，节点 1 的右子树）

• 栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(4)：root=4，断点在"判断是否为叶子节点后"]
• 执行步骤：
  1. 检查 root=4 不为空，不触发规则 1。
  2. 检查 root=4 的左、右子树都不为空（有节点 5 和 6），所以不是叶子节点，不触发规则 2。
  3. 执行规则 3：统计左子树叶子节点个数→ 调用 countLeafNodes(root->left)，也就是 countLeafNodes(5)（节点 4 的左子树是 5）。
  4. 栈帧变化：暂停 countLeafNodes(4)（断点记在 " 计算完 countLeafNodes(5) 后，要计算 rightLeafCount"），新增 countLeafNodes(5) 的栈帧压入栈。此时栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(4)（暂停）, countLeafNodes(5)：root=5，断点在"判断是否为叶子节点后"]。
• 当前返回结果：1（leftLeafCount = 1）。

8. 执行 countLeafNodes(5)（节点 5，节点 4 的左子树）

• 栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(4)（暂停）, countLeafNodes(5)：root=5，断点在"判断是否为叶子节点后"]
• 执行步骤：
  1. 检查 root=5 不为空，不触发规则 1。
  2. 检查 root=5 的左、右子树都为空，所以是叶子节点，触发规则 2，返回 1。
  3. 执行 return，撕掉 countLeafNodes(5) 的栈帧（弹出栈），回到 countLeafNodes(4) 的 "断点位置"—— 也就是 " 计算完 countLeafNodes(left) 后，准备计算 rightLeafCount"。
• 当前返回结果：1（leftLeafCount = 1）。

9. 回到 countLeafNodes(4)，继续执行

• 栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(4)：root=4，断点在"判断是否为叶子节点后"]
• 执行步骤：
  1. 执行规则 3：统计右子树叶子节点个数→ 调用 countLeafNodes(root->right)，也就是 countLeafNodes(6)（节点 4 的右子树是 6）。
  2. 栈帧变化：暂停 countLeafNodes(4)（断点记在 " 计算完 countLeafNodes(6) 后，要返回结果 "），新增 countLeafNodes(6) 的栈帧压入栈。此时栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(4)（暂停）, countLeafNodes(6)：root=6，断点在"判断是否为叶子节点后"]。
• 当前返回结果：1（leftLeafCount = 1）。

10. 执行 countLeafNodes(6)（节点 6，节点 4 的右子树）

• 栈状态：[countLeafNodes(1)（暂停）, countLeafNodes(4)（暂停）, countLeafNodes(6)：root=6，断点在"判断是否为叶子节点后"]
• 执行步骤：
  1. 检查 root=6 不为空，不触发规则 1。
  2. 检查 root=6 的左、右子树都为空，所以是叶子节点，触发规则 2，返回 1。
  3. 执行 return，撕掉 countLeafNodes(6) 的栈帧（弹出栈），回到 countLeafNodes(4) 的 "断点位置"—— 也就是 " 计算完 countLeafNodes(right) 后，准备返回结果 "。
  4. countLeafNodes(4) 的 leftLeafCount = 1，rightLeafCount = 1，所以返回 1 + 1 = 2。
  5. 执行 return，撕掉 countLeafNodes(4) 的栈帧（弹出栈），回到 countLeafNodes(1) 的 "断点位置"—— 也就是 " 计算完 countLeafNodes(right) 后，准备返回结果 "。
• 当前返回结果：2（rightLeafCount = 2）。

11. 回到 countLeafNodes(1)，继续执行

• 栈状态：[countLeafNodes(1)：root=1，断点在"判断是否为叶子节点后"]
• 执行步骤：
  1. countLeafNodes(1) 的 leftLeafCount = 1，rightLeafCount = 2，所以返回 1 + 2 = 3。
  2. 执行 return，撕掉 countLeafNodes(1) 的栈帧（弹出栈）。
• 当前返回结果：3。

12. 统计叶子节点个数结束

• 栈状态：空（所有栈帧都已弹出）
• 最终返回结果：3
• 核心统计逻辑：整棵树的叶子节点个数 = 左子树叶子节点数（1） + 右子树叶子节点数（2） = 3

五、总结：统计叶子节点个数的核心要点

通过上面的详细拆解，我们可以总结出统计二叉树叶子节点个数的几个核心要点：

1. 统计规则：严格遵循 "空节点返回 0，叶子节点返回 1，非叶子节点返回左右子树之和"，这是递归统计的核心公式。

2. 叶子节点定义：叶子节点是左、右子树都为空的节点（度为 0 的节点），这是判断的关键条件。需要同时检查左、右两个子树是否都为空，缺一不可。

3. 递归本质：利用二叉树的递归结构，将 "统计整棵树" 拆成 "统计左子树 + 统计右子树"，只有叶子节点才会计数。递归的魅力在于将复杂问题分解为相似的简单问题。

4. 终止条件：遇到空节点返回 0，遇到叶子节点返回 1，这两个条件确保递归能正常结束，避免无限循环。

5. 栈的作用：递归调用时，函数栈自动记录 "未完成的父节点计算"，确保左右子树都统计完后能回到父节点，继续累加计算。栈的这种特性使得递归能够正确地处理嵌套结构。

6. 时间复杂度：O (n)，其中 n 是树的节点个数，因为每个节点都会被访问并判断一次。这种线性时间复杂度说明算法效率很高。

7. 空间复杂度：O (h)，其中 h 是树的高度，主要是递归调用栈的空间开销。在最坏情况下（单链树），h = n，空间复杂度为 O (n)；在最好情况下（完全二叉树），h = log n，空间复杂度为 O (log n)。

8. 应用场景：

   • 数据结构分析：统计树的结构特征
   • 电路设计：检测电路的端点
   • 网络拓扑：统计终端设备数量
   • 产品质量检验：计数最终产品
   • 植物学研究：监测植物生长状况

掌握了统计叶子节点个数的方法，你会发现它和统计总节点数的逻辑是相通的 —— 都是 "递归拆解 + 栈帧管理"，区别只是处理节点的方式不同。这种 "统一逻辑 + 差异化处理" 的特点，正是二叉树操作的精髓所在。记住：统计叶子节点个数的核心就是 "只有末端节点才计数，非末端节点只汇总"，这是解决很多二叉树筛选问题的基础。

下面是完整代码：

//求出二叉树的叶子节点个数
int binarytreeleafsize(btn* root)
{//叶子结点是指树结构中没有子结点的节点，也称为终端结点或度为0的结点。//它们是树的最末端节点，通常用于表示数据结构中的最终数据或状态//如果碰到了空节点，就代表它是没有节点的//就得返回0//这是递归的边界条件，防止无限递归。if (root == NULL){return 0;}//同时，如果只有一个根节点，它的左右子树全部为空//就代表它是叶子节点，我们要返回1,代表有一个叶子节点了//其实这也是为了和上面的二叉树全部的节点个数区分开来//上面是只要你是根节点，都要加一//而在我们的查找叶子节点函数中//则是只有某个根节点的左子树和右子树都为空//此时证明它是叶子节点//那么这个时候才能加一if (root->left == NULL && root->right == NULL){return 1;}//接着我们就得使用递归，去将每个根节点的左右子树都遍历一遍//递归的核心是将大问题分解为相似的小问题，//这里将 "求整棵树的叶子节点数" 分解为//"求左子树的叶子节点数" 和 "求右子树的叶子节点数" 之和。return binarytreeleafsize(root->left) + binarytreeleafsize(root->right);}

我觉得大家要理解，就必须要结合着上面所说的例子进行详细理解。其实本质上还是不难的。

求出二叉树的深度/高度：

这个又是一个二叉树的经典操作，即一棵二叉树有多深，以下图为例：

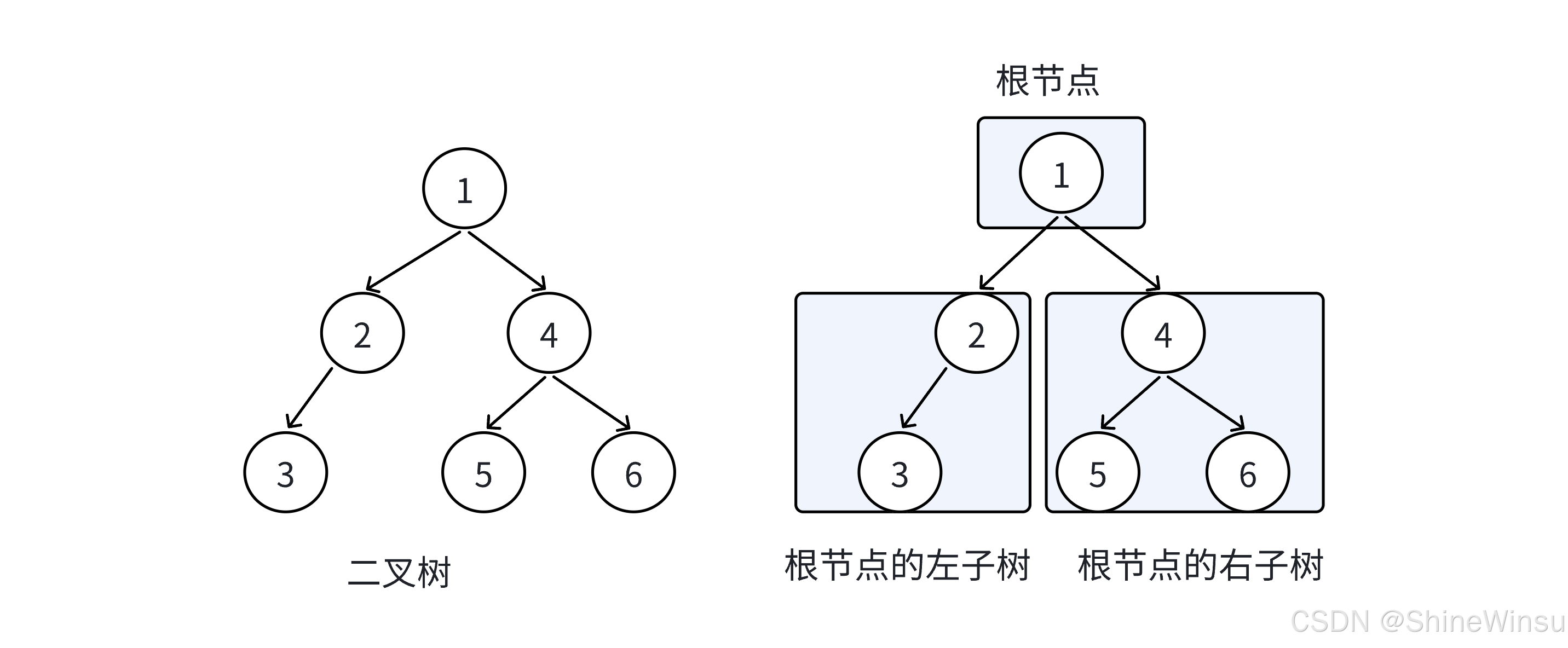
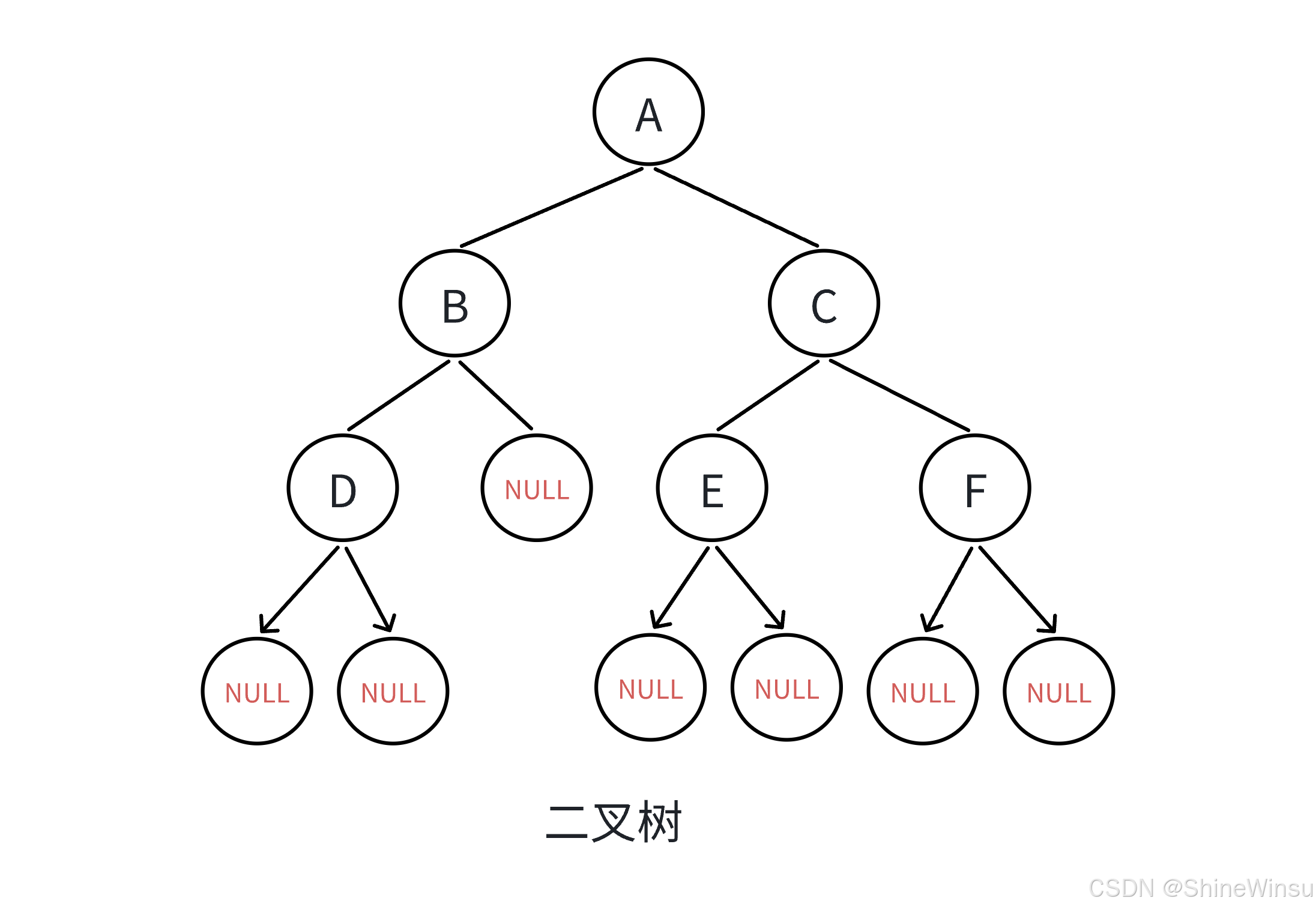
我们不难看出，这一棵二叉树的深度是3层，那么，我们要怎么让编译器去帮我们数一棵二叉树的深度呢？

其实，我们依旧是要利用递归去解决这个问题，我们观察一下上图，上面的3层我们是怎么得到的呢？除了直接数，我们也可以根据刚才这课二叉树最上面的根节点的左右子树中，哪棵子树的深度更大，然后再加1得到，这个加一是为了算上最上面这个根节点的那一层。由上图，两个子树一样深，那么我们就任取一个，再加一即可，最后得出结果为3，正好符合。

上面所说的，便可以用来我们的递归，我们依旧是借助递归去拆分，去统计每一个根节点的左右子树深度，然后再去比较左右子树中哪个更深，选取更深的那一个子树的深度去执行加一，那么这个时候的结果便是这个根节点到二叉树最下面的深度。并且由此不断递归，直到最后变成统计二叉树最上面的一个根节点的左右子树深度，并且选取较深的树的深度执行加一，那么这个时候得出的结果就是一整棵二叉树的深度了。

二叉树的深度（也叫高度）是指从根节点到最远叶子节点的最长路径上的节点数。统计二叉树深度和之前的统计操作核心逻辑很像，都是用递归把 "统计整棵树" 拆成 "统计子树" 的小问题，但关键区别在于：深度是取左右子树深度的最大值再加 1。刚开始可能会有点绕，但跟着例子一步步走，你会发现：哦，原来和之前的统计逻辑是通的，只是把 "计数" 换成了 "求最大值" 而已！

我们还是以之前的二叉树（根节点为 1，左子树以 2 为根，右子树以 4 为根）为例，先把树的结构再明确一下，方便后续对照：

        1        （根节点）/ \2   4      （第2层）/   / \3   5   6    （第3层）

在这棵树中，从根节点 1 到最远叶子节点 3、5、6 的路径长度都是 3（经过 3 个节点），所以树的深度是 3。

接下来，咱们从 "执行步骤"" 生活化例子 ""代码实现"" 递归栈帧细节 " 四个部分，把统计二叉树深度彻底讲透。

一、统计二叉树深度的执行步骤（核心：取左右子树深度的最大值再加 1）

统计二叉树深度的规则是：

1. 如果当前节点为空，返回 0（空树的深度为 0）
2. 否则，返回左子树深度和右子树深度中的最大值 + 1（当前节点的深度是子树深度的最大值加 1）

而且对左、右子树的深度统计，也完全遵循这个规则，直到遇到空节点才停止。

咱们一步一步拆解整个过程：

步骤 1：从整棵树的根节点 1 开始，计算它的深度

节点 1 不为空，按照规则 2，需要计算左子树（以 2 为根的子树）的深度、右子树（以 4 为根的子树）的深度，然后取最大值再加 1。

子步骤 1.1：计算节点 2 所在左子树的深度

节点 2 不为空，按照规则 2，需要计算它的左子树（以 3 为根的子树）的深度、右子树（空）的深度，然后取最大值再加 1。

子步骤 1.1.1：计算节点 3 所在左子树的深度

节点 3 不为空，计算它的左子树（空）的深度（返回 0）、右子树（空）的深度（返回 0），取最大值 0 再加 1，结果为 0 + 1 = 1。所以节点 3 所在子树的深度是 1。

子步骤 1.1.2：节点 2 的右子树为空，深度为 0。取左子树深度 1 和右子树深度 0 的最大值 1，再加 1，所以节点 2 所在子树的深度是 1 + 1 = 2。

步骤 2：计算节点 1 的右子树（以 4 为根的子树）的深度

节点 4 不为空，按照规则 2，需要计算它的左子树（以 5 为根的子树）的深度、右子树（以 6 为根的子树）的深度，然后取最大值再加 1。

子步骤 2.1：计算节点 5 所在左子树的深度

节点 5 不为空，其左子树和右子树都为空，所以节点 5 所在子树的深度是 0 + 1 = 1。

子步骤 2.2：计算节点 6 所在右子树的深度

节点 6 不为空，其左子树和右子树都为空，所以节点 6 所在子树的深度是 0 + 1 = 1。

取左子树深度 1 和右子树深度 1 的最大值 1，再加 1，所以节点 4 所在子树的深度是 1 + 1 = 2。

步骤 3：整棵树的深度

取左子树深度 2 和右子树深度 2 的最大值 2，再加 1，所以整棵树的深度是 2 + 1 = 3，与我们手动计算的结果一致。

二、生活化例子："公司组织架构层级统计"

把二叉树想象成一个公司的组织架构，根节点是 CEO，每个节点代表一个员工，子节点代表该员工的下属。统计树的深度就像是统计公司的管理层级 —— 从 CEO 到最基层员工的层级数。

1. 节点对应的公司职位明确

• 根节点 1：CEO（公司最高层）
• 左子树根 2：技术总监（直接向 CEO 汇报）
• 左子树的左子树 3：开发团队组长（直接向技术总监汇报）
• 右子树根 4：业务总监（直接向 CEO 汇报）
• 右子树的左子树 5：销售团队组长（直接向业务总监汇报）
• 右子树的右子树 6：市场团队组长（直接向业务总监汇报）

2. 统计管理层级的流程（人力资源部门的工作）

第一步：统计技术部门的层级

HR 部门开始统计公司的管理层级，先从技术部门开始：

"我们需要知道从 CEO 到最基层员工有多少个层级。先看看技术部门的情况。"HR 经理说道。

技术总监 2 汇报："我管理着开发团队，开发团队由组长 3 负责。"开发团队组长 3 汇报："我没有下属员工了，我是最基层的管理者。"HR 经理记录："开发团队组长 3 是第 3 层级（CEO → 技术总监 → 开发组长），技术部门的层级是 3 层。"

第二步：统计业务部门的层级

接着 HR 部门统计业务部门：

业务总监 4 汇报："我管理着销售团队和市场团队，分别由组长 5 和组长 6 负责。"销售团队组长 5 汇报："我没有下属员工了。"市场团队组长 6 汇报："我也没有下属员工了。"HR 经理记录："销售团队组长 5 和市场团队组长 6 都是第 3 层级（CEO → 业务总监 → 销售 / 市场组长），业务部门的层级也是 3 层。"

第三步：统计全公司的管理层级

HR 经理汇总数据："技术部门和业务部门的最高层级都是 3 层，所以公司的管理层级是 3 层。"

这意味着从 CEO 到最基层的团队组长，需要经过 3 个层级，与我们树的深度计算结果一致。

3. 统计二叉树深度的本质："取最长路径"

从公司组织架构的例子能看出来，统计二叉树深度的逻辑是 "取左右子树深度的最大值再加 1"。就像公司的管理层级，我们关心的是从最高层到最基层的最长路径，而不是平均路径。这种 "求最大值" 的思想在很多实际场景中都有应用，比如：

• 建筑设计中的 "楼层高度计算"
• 网络传输中的 "最长路径分析"
• 项目管理中的 "任务层级规划"

三、统计二叉树深度的递归代码实现

统计二叉树深度的代码逻辑清晰，基于 "空节点返回 0，非空节点返回左右子树深度的最大值加 1" 的规则。咱们直接上代码，关键地方加了注释：

// 1. 先定义二叉树节点结构体（和之前一致）
typedef struct BinaryTreeNode {int data;                       // 节点存储的数据struct BinaryTreeNode* left;    // 指向左子节点的指针struct BinaryTreeNode* right;   // 指向右子节点的指针
} btn;  // 结构体别名，简化后续使用// 2. 统计二叉树深度的函数：参数是当前子树的根节点，返回该子树的深度
int treeDepth(btn* root) {// 规则1：如果当前节点是空，返回0（空树的深度为0）if (root == NULL) {return 0;}// 规则2：否则，返回左子树深度和右子树深度中的最大值 + 1int leftDepth = treeDepth(root->left);   // 计算左子树的深度int rightDepth = treeDepth(root->right); // 计算右子树的深度// 返回左右子树深度的最大值 + 1（当前节点的深度）return (leftDepth > rightDepth ? leftDepth : rightDepth) + 1;
}

代码的核心就是计算左右子树的深度，然后取最大值加 1。比如咱们的示例树，调用 treeDepth(root)（root 指向节点 1），最终会返回 3，和我们手动计算的结果一致。

四、统计二叉树深度的递归栈帧细节（彻底理解 "怎么跑的"）

为了彻底理解递归统计二叉树深度的过程，我们还是以 treeDepth(root)（root 指向节点 1）为例，拆解每一步的栈状态、执行操作和返回结果。

核心概念：函数调用栈

递归的时候，每次调用 treeDepth 函数，系统都会在 "函数栈" 里新增一个 "栈帧"—— 这个栈帧记录着当前函数的参数（比如 root 指向哪个节点）、局部变量（leftDepth、rightDepth）以及 "下一步要执行的代码位置"（断点）。当函数执行到 return，这张 "便签" 就会被撕掉（栈帧弹出），程序回到上一张便签的 "断点位置" 继续执行。

1. 初始调用：treeDepth(1)（根节点 1）

• 栈状态（从上到下是最近调用的函数，栈帧里记录 "函数名 + root 值 + 断点"）：[treeDepth(1)：root=1，断点在"计算 leftDepth 后"]
• 执行步骤：
  1. 检查 root=1 不为空，不触发规则 1。
  2. 执行规则 2：计算左子树深度→ 调用 treeDepth(root->left)，也就是 treeDepth(2)（节点 1 的左子树是 2）。
  3. 栈帧变化：把 treeDepth(1) 的栈帧暂停（断点记在 " 计算完 treeDepth(2) 后，要计算 rightDepth"），新增 treeDepth(2) 的栈帧压入栈。此时栈状态：[treeDepth(1)（暂停）, treeDepth(2)：root=2，断点在"计算 leftDepth 后"]。
• 当前返回结果：无（还没到返回步骤）。

2. 执行 treeDepth(2)（节点 2，节点 1 的左子树）

• 栈状态：[treeDepth(1)（暂停）, treeDepth(2)：root=2，断点在"计算 leftDepth 后"]
• 执行步骤：
  1. 检查 root=2 不为空，不触发规则 1。
  2. 执行规则 2：计算左子树深度→ 调用 treeDepth(root->left)，也就是 treeDepth(3)（节点 2 的左子树是 3）。
  3. 栈帧变化：暂停 treeDepth(2)（断点记在 " 计算完 treeDepth(3) 后，要计算 rightDepth"），新增 treeDepth(3) 的栈帧压入栈。此时栈状态：[treeDepth(1)（暂停）, treeDepth(2)（暂停）, treeDepth(3)：root=3，断点在"计算 leftDepth 后"]。
• 当前返回结果：无。

3. 执行 treeDepth(3)（节点 3，节点 2 的左子树）

• 栈状态：[treeDepth(1)（暂停）, treeDepth(2)（暂停）, treeDepth(3)：root=3，断点在"计算 leftDepth 后"]
• 执行步骤：
  1. 检查 root=3 不为空，不触发规则 1。
  2. 执行规则 2：计算左子树深度→ 调用 treeDepth(root->left)，也就是 treeDepth(NULL)（节点 3 的左子树是空）。
  3. 栈帧变化：暂停 treeDepth(3)（断点记在 " 计算完 treeDepth(NULL) 后，要计算 rightDepth"），新增 treeDepth(NULL) 的栈帧压入栈。此时栈状态：[treeDepth(1)（暂停）, treeDepth(2)（暂停）, treeDepth(3)（暂停）, treeDepth(NULL)：root=NULL]。
• 当前返回结果：无。

4. 执行 treeDepth(NULL)（节点 3 的左子树）

• 栈状态：[treeDepth(1)（暂停）, treeDepth(2)（暂停）, treeDepth(3)（暂停）, treeDepth(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发规则 1，返回 0。
  2. 执行 return，撕掉 treeDepth(NULL) 的栈帧（弹出栈），回到 treeDepth(3) 的 "断点位置"—— 也就是 " 计算完 treeDepth(left) 后，准备计算 rightDepth"。
• 当前返回结果：0（leftDepth = 0）。

5. 回到 treeDepth(3)，继续执行

• 栈状态：[treeDepth(1)（暂停）, treeDepth(2)（暂停）, treeDepth(3)：root=3，断点在"计算 leftDepth 后"]
• 执行步骤：
  1. 执行规则 2：计算右子树深度→ 调用 treeDepth(root->right)，也就是 treeDepth(NULL)（节点 3 的右子树是空）。
  2. 栈帧变化：暂停 treeDepth(3)（断点记在 " 计算完 treeDepth(NULL) 后，要返回结果 "），新增 treeDepth(NULL) 的栈帧压入栈。此时栈状态：[treeDepth(1)（暂停）, treeDepth(2)（暂停）, treeDepth(3)（暂停）, treeDepth(NULL)：root=NULL]。
• 当前返回结果：0（leftDepth = 0）。

6. 再执行 treeDepth(NULL)（节点 3 的右子树）

• 栈状态：[treeDepth(1)（暂停）, treeDepth(2)（暂停）, treeDepth(3)（暂停）, treeDepth(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发规则 1，返回 0。
  2. 执行 return，撕掉 treeDepth(NULL) 的栈帧（弹出栈），回到 treeDepth(3) 的 "断点位置"—— 也就是 " 计算完 treeDepth(right) 后，准备返回结果 "。
  3. treeDepth(3) 的 leftDepth = 0，rightDepth = 0，取最大值 0 再加 1，所以返回 0 + 1 = 1。
  4. 执行 return，撕掉 treeDepth(3) 的栈帧（弹出栈），回到 treeDepth(2) 的 "断点位置"—— 也就是 " 计算完 treeDepth(left) 后，准备计算 rightDepth"。
• 当前返回结果：1（leftDepth = 1）。

7. 回到 treeDepth(2)，继续执行

• 栈状态：[treeDepth(1)（暂停）, treeDepth(2)：root=2，断点在"计算 leftDepth 后"]
• 执行步骤：
  1. 执行规则 2：计算右子树深度→ 调用 treeDepth(root->right)，也就是 treeDepth(NULL)（节点 2 的右子树是空）。
  2. 栈帧变化：暂停 treeDepth(2)（断点记在 " 计算完 treeDepth(NULL) 后，要返回结果 "），新增 treeDepth(NULL) 的栈帧压入栈。此时栈状态：[treeDepth(1)（暂停）, treeDepth(2)（暂停）, treeDepth(NULL)：root=NULL]。
• 当前返回结果：1（leftDepth = 1）。

8. 执行 treeDepth(NULL)（节点 2 的右子树）

• 栈状态：[treeDepth(1)（暂停）, treeDepth(2)（暂停）, treeDepth(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发规则 1，返回 0。
  2. 执行 return，撕掉 treeDepth(NULL) 的栈帧（弹出栈），回到 treeDepth(2) 的 "断点位置"—— 也就是 " 计算完 treeDepth(right) 后，准备返回结果 "。
  3. treeDepth(2) 的 leftDepth = 1，rightDepth = 0，取最大值 1 再加 1，所以返回 1 + 1 = 2。
  4. 执行 return，撕掉 treeDepth(2) 的栈帧（弹出栈），回到 treeDepth(1) 的 "断点位置"—— 也就是 " 计算完 treeDepth(left) 后，准备计算 rightDepth"。
• 当前返回结果：2（leftDepth = 2）。

9. 回到 treeDepth(1)，继续执行

• 栈状态：[treeDepth(1)：root=1，断点在"计算 leftDepth 后"]
• 执行步骤：
  1. 执行规则 2：计算右子树深度→ 调用 treeDepth(root->right)，也就是 treeDepth(4)（节点 1 的右子树是 4）。
  2. 栈帧变化：暂停 treeDepth(1)（断点记在 " 计算完 treeDepth(4) 后，要返回结果 "），新增 treeDepth(4) 的栈帧压入栈。此时栈状态：[treeDepth(1)（暂停）, treeDepth(4)：root=4，断点在"计算 leftDepth 后"]。
• 当前返回结果：2（leftDepth = 2）。

10. 执行 treeDepth(4)（节点 4，节点 1 的右子树）

• 栈状态：[treeDepth(1)（暂停）, treeDepth(4)：root=4，断点在"计算 leftDepth 后"]
• 执行步骤：
  1. 检查 root=4 不为空，不触发规则 1。
  2. 执行规则 2：计算左子树深度→ 调用 treeDepth(root->left)，也就是 treeDepth(5)（节点 4 的左子树是 5）。
  3. 栈帧变化：暂停 treeDepth(4)（断点记在 " 计算完 treeDepth(5) 后，要计算 rightDepth"），新增 treeDepth(5) 的栈帧压入栈。此时栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(5)：root=5，断点在"计算 leftDepth 后"]。
• 当前返回结果：2（leftDepth = 2）。

11. 执行 treeDepth(5)（节点 5，节点 4 的左子树）

• 栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(5)：root=5，断点在"计算 leftDepth 后"]
• 执行步骤：
  1. 检查 root=5 不为空，不触发规则 1。
  2. 执行规则 2：计算左子树深度→ 调用 treeDepth(root->left)，也就是 treeDepth(NULL)（节点 5 的左子树是空）。
  3. 栈帧变化：暂停 treeDepth(5)（断点记在 " 计算完 treeDepth(NULL) 后，要计算 rightDepth"），新增 treeDepth(NULL) 的栈帧压入栈。此时栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(5)（暂停）, treeDepth(NULL)：root=NULL]。
• 当前返回结果：2（leftDepth = 2）。

12. 执行 treeDepth(NULL)（节点 5 的左子树）

• 栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(5)（暂停）, treeDepth(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发规则 1，返回 0。
  2. 执行 return，撕掉 treeDepth(NULL) 的栈帧（弹出栈），回到 treeDepth(5) 的 "断点位置"—— 也就是 " 计算完 treeDepth(left) 后，准备计算 rightDepth"。
• 当前返回结果：0（leftDepth = 0）。

13. 回到 treeDepth(5)，继续执行

• 栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(5)：root=5，断点在"计算 leftDepth 后"]
• 执行步骤：
  1. 执行规则 2：计算右子树深度→ 调用 treeDepth(root->right)，也就是 treeDepth(NULL)（节点 5 的右子树是空）。
  2. 栈帧变化：暂停 treeDepth(5)（断点记在 " 计算完 treeDepth(NULL) 后，要返回结果 "），新增 treeDepth(NULL) 的栈帧压入栈。此时栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(5)（暂停）, treeDepth(NULL)：root=NULL]。
• 当前返回结果：0（leftDepth = 0）。

14. 再执行 treeDepth(NULL)（节点 5 的右子树）

• 栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(5)（暂停）, treeDepth(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发规则 1，返回 0。
  2. 执行 return，撕掉 treeDepth(NULL) 的栈帧（弹出栈），回到 treeDepth(5) 的 "断点位置"—— 也就是 " 计算完 treeDepth(right) 后，准备返回结果 "。
  3. treeDepth(5) 的 leftDepth = 0，rightDepth = 0，取最大值 0 再加 1，所以返回 0 + 1 = 1。
  4. 执行 return，撕掉 treeDepth(5) 的栈帧（弹出栈），回到 treeDepth(4) 的 "断点位置"—— 也就是 " 计算完 treeDepth(left) 后，准备计算 rightDepth"。
• 当前返回结果：1（leftDepth = 1）。

15. 回到 treeDepth(4)，继续执行

• 栈状态：[treeDepth(1)（暂停）, treeDepth(4)：root=4，断点在"计算 leftDepth 后"]
• 执行步骤：
  1. 执行规则 2：计算右子树深度→ 调用 treeDepth(root->right)，也就是 treeDepth(6)（节点 4 的右子树是 6）。
  2. 栈帧变化：暂停 treeDepth(4)（断点记在 " 计算完 treeDepth(6) 后，要返回结果 "），新增 treeDepth(6) 的栈帧压入栈。此时栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(6)：root=6，断点在"计算 leftDepth 后"]。
• 当前返回结果：1（leftDepth = 1）。

16. 执行 treeDepth(6)（节点 6，节点 4 的右子树）

• 栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(6)：root=6，断点在"计算 leftDepth 后"]
• 执行步骤：
  1. 检查 root=6 不为空，不触发规则 1。
  2. 执行规则 2：计算左子树深度→ 调用 treeDepth(root->left)，也就是 treeDepth(NULL)（节点 6 的左子树是空）。
  3. 栈帧变化：暂停 treeDepth(6)（断点记在 " 计算完 treeDepth(NULL) 后，要计算 rightDepth"），新增 treeDepth(NULL) 的栈帧压入栈。此时栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(6)（暂停）, treeDepth(NULL)：root=NULL]。
• 当前返回结果：1（leftDepth = 1）。

17. 执行 treeDepth(NULL)（节点 6 的左子树）

• 栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(6)（暂停）, treeDepth(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发规则 1，返回 0。
  2. 执行 return，撕掉 treeDepth(NULL) 的栈帧（弹出栈），回到 treeDepth(6) 的 "断点位置"—— 也就是 " 计算完 treeDepth(left) 后，准备计算 rightDepth"。
• 当前返回结果：0（leftDepth = 0）。

18. 回到 treeDepth(6)，继续执行

• 栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(6)：root=6，断点在"计算 leftDepth 后"]
• 执行步骤：
  1. 执行规则 2：计算右子树深度→ 调用 treeDepth(root->right)，也就是 treeDepth(NULL)（节点 6 的右子树是空）。
  2. 栈帧变化：暂停 treeDepth(6)（断点记在 " 计算完 treeDepth(NULL) 后，要返回结果 "），新增 treeDepth(NULL) 的栈帧压入栈。此时栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(6)（暂停）, treeDepth(NULL)：root=NULL]。
• 当前返回结果：0（leftDepth = 0）。

19. 再执行 treeDepth(NULL)（节点 6 的右子树）

• 栈状态：[treeDepth(1)（暂停）, treeDepth(4)（暂停）, treeDepth(6)（暂停）, treeDepth(NULL)：root=NULL]
• 执行步骤：
  1. 检查 root=NULL，触发规则 1，返回 0。
  2. 执行 return，撕掉 treeDepth(NULL) 的栈帧（弹出栈），回到 treeDepth(6) 的 "断点位置"—— 也就是 " 计算完 treeDepth(right) 后，准备返回结果 "。
  3. treeDepth(6) 的 leftDepth = 0，rightDepth = 0，取最大值 0 再加 1，所以返回 0 + 1 = 1。
  4. 执行 return，撕掉 treeDepth(6) 的栈帧（弹出栈），回到 treeDepth(4) 的 "断点位置"—— 也就是 " 计算完 treeDepth(right) 后，准备返回结果 "。
• 当前返回结果：1（rightDepth = 1）。

20. 回到 treeDepth(4)，继续执行

• 栈状态：[treeDepth(1)（暂停）, treeDepth(4)：root=4，断点在"计算 rightDepth 后"]
• 执行步骤：
  1. treeDepth(4) 的 leftDepth = 1，rightDepth = 1，取最大值 1 再加 1，所以返回 1 + 1 = 2。
  2. 执行 return，撕掉 treeDepth(4) 的栈帧（弹出栈），回到 treeDepth(1) 的 "断点位置"—— 也就是 " 计算完 treeDepth(right) 后，准备返回结果 "。
• 当前返回结果：2（rightDepth = 2）。

21. 回到 treeDepth(1)，继续执行

• 栈状态：[treeDepth(1)：root=1，断点在"计算 rightDepth 后"]
• 执行步骤：
  1. treeDepth(1) 的 leftDepth = 2，rightDepth = 2，取最大值 2 再加 1，所以返回 2 + 1 = 3。
  2. 执行 return，撕掉 treeDepth(1) 的栈帧（弹出栈）。
• 当前返回结果：3。

22. 统计二叉树深度结束

• 栈状态：空（所有栈帧都已弹出）
• 最终返回结果：3
• 核心统计逻辑：整棵树的深度 = max (左子树深度（2）, 右子树深度（2）) + 1 = 3

五、总结：统计二叉树深度的核心要点

通过上面的详细拆解，我们可以总结出统计二叉树深度的几个核心要点：

1. 统计规则：严格遵循 "空节点返回 0，非空节点返回左右子树深度的最大值加 1"，这是递归统计的核心公式。

2. 深度定义：二叉树的深度是从根节点到最远叶子节点的最长路径上的节点数。需要注意的是，有些定义中深度是指路径上的边数（此时空树深度为 - 1），但我们这里采用节点数的定义。

3. 递归本质：利用二叉树的递归结构，将 "计算整棵树深度" 拆成 "计算左子树深度 + 计算右子树深度 + 取最大值加 1"，子树的深度计算逻辑与整棵树完全一致。

4. 终止条件：遇到空节点返回 0，这是递归能正常结束的关键，避免无限循环。

5. 栈的作用：递归调用时，函数栈自动记录 "未完成的父节点计算"，确保左右子树深度都计算完后能回到父节点，继续进行最大值比较和加 1 操作。

6. 时间复杂度：O (n)，其中 n 是树的节点个数，因为每个节点都会被访问并计算一次。

7. 空间复杂度：O (h)，其中 h 是树的高度，主要是递归调用栈的空间开销。在最坏情况下（单链树），h = n，空间复杂度为 O (n)；在最好情况下（完全二叉树），h = log n，空间复杂度为 O (log n)。

8. 应用场景：

   • 数据结构分析：评估树的平衡程度
   • 算法优化：确定递归深度限制
   • 数据库索引：影响查询效率
   • 人工智能：神经网络的深度设计

掌握了统计二叉树深度的方法，你会发现它和之前的统计操作逻辑是相通的 —— 都是 "递归拆解 + 栈帧管理"，区别只是处理节点的方式不同。这种 "统一逻辑 + 差异化处理" 的特点，正是二叉树操作的精髓所在。记住：统计二叉树深度的核心就是 "取左右子树深度的最大值再加 1"，这是解决很多二叉树路径问题的基础。

下面是完整代码：

////二叉树的深度/高度
//int binarytreedepth(btn* root)
//{
//	//二叉树的深度可以通过以下逻辑递归计算：
//	//空节点的深度为 0（递归终止条件）
//	//非空节点的深度 = 其左子树深度与右子树深度的最大值 + 1
//	//（ + 1 是因为当前节点本身算一层）
//
//
//	//我们依旧是使用递归的思想来解决
//	//当节点为NULL时，返回0，代表没有这一层
//	if (root == NULL)
//	{
//		return 0;
//	}
//
//	//接着我们要分别判断最上面的根节点的左右子树
//	//的层数，看哪个层数最大，就要那个，同时要加上1
//	//这个1是表示当前根节点的那一层
//	return binarytreedepth(root->left) > binarytreedepth(root->right) ? binarytreedepth(root->left) + 1 : binarytreedepth(root->right) + 1;
//}//但是上面的方法，效率不高//二叉树的深度/高度
int binarytreedepth(btn* root)
{//二叉树的深度可以通过以下逻辑递归计算：//空节点的深度为 0（递归终止条件）//非空节点的深度 = 其左子树深度与右子树深度的最大值 + 1//（ + 1 是因为当前节点本身算一层）//我们依旧是使用递归的思想来解决//当节点为NULL时，返回0，代表没有这一层if (root == NULL){return 0;}//接着我们要分别判断根节点的左右子树的层数，//看哪个层数最大，就要那个，同时要加上1//这个1是表示当前根节点的那一层int leftdepth = binarytreedepth(root->left);int rightdepth = binarytreedepth(root->right);//我们得设置变量去保存深度//不难每次都会重复调用递归，导致效率低下//这是因为我们要比较大小，所以就会重复递归//并不是像上面直接返回return leftdepth > rightdepth ? leftdepth + 1 : rightdepth + 1;
}

我觉得大家要理解，就必须要结合着上面所说的例子进行详细理解。其实本质上还是不难的。

下面给出我的手写解析：

求出二叉树第k层结点个数：

这一个部分相对于上面的几个部分，会更加难以理解一些说实话。

这个部分是要求，我们要统计出二叉树中第k层的节点有几个，这里注意一下，在二叉树中，我们是从第一层开始数的，并不是从第零层开始数的。

我们依旧以下图为例子：

假设我们要求这棵二叉树中第2层的节点个数，那么根据上图，我们一眼看出，有2个。

那么我们又要怎么利用递归去让编译器帮我们统计呢？

其实这也是一个非常巧妙的思想，在这里我真的是不得不感叹一句，先人的智慧，是真的厉害呀。

这个思想就是类似于大哥指使小弟，小弟指使它的小弟，小弟的小弟指使它的小弟，直到某一个小弟没有小弟了，那么这个时候，只能这个小弟自己干活，然后再返回，很显然，这也是我们递归的思想。

//比如一共5层，我们要找第3层
//那么当k到了1的时候，就相当于是到了第3层
//因为当k还为3的时候，此时是在第一层
//而后k-1，此时k==2，代表向下移动1层，也就是到了第二层
//接着再执行k-1，此时k==1，代表向下移动1层，也就是到了第三层
//那么这个时候就得停止继续往下移动了
//因为我们已经到了我们要查找的层数
//并且，我们还得记录我们所到这一层的节点的数量
//其实就是为1，因为我们此时是代表着移动到了这一层的某一个节点
//可能是在左子树，也可能是在右子树，还有可能是根节点
//但是都是一个节点，所以我们要返回1
//那么这个时候自然就要返回回去了
//但是在返回回去的同时，我们要进行加一
//其实就是记录一下这里有个节点

大家可以结合图像进行理解，那么实现这个功能最主要的，一个是要记得返回左子树相加右子树，这样子才能实现累加，还有一个就是我们要使用判断语句去判断是否到了第k层，并且要去看到第k层时的这一个节点是不是为NULL，是的话，我们就得返回0，代表这里没有节点，不是的话，就得返回1，代表这里有个节点。同时判断是否到了第k层的关键就是看k是否为1了。

统计第 k 层节点个数的核心思想是：如果当前节点在第 k 层，就计数；否则，递归统计左、右子树的第 k-1 层节点个数。刚开始可能会觉得有点绕，但跟着例子一步步走，你会发现：哦，原来就是 "逐层深入" 的过程，每向下一层，k 值就减 1，直到 k=1 时开始计数！

我们还是以之前的二叉树（根节点为 1，左子树以 2 为根，右子树以 4 为根）为例，先把树的结构再明确一下，方便后续对照：

        1        （根节点，第1层）/ \2   4      （第2层）/   / \3   5   6    （第3层）

在这棵树中：

• 第 1 层：只有节点 1，共 1 个节点
• 第 2 层：有节点 2 和节点 4，共 2 个节点
• 第 3 层：有节点 3、节点 5 和节点 6，共 3 个节点
• 第 4 层及以上：没有节点，共 0 个节点

接下来，咱们从 "执行步骤"" 生活化例子 ""代码实现"" 递归栈帧细节 " 四个部分，把统计二叉树第 k 层节点个数彻底讲透。

一、统计二叉树第 k 层节点个数的执行步骤（核心：逐层深入，k=1 时计数）

统计二叉树第 k 层节点个数的规则是：

1. 如果当前节点为空，返回 0（空树没有节点）
2. 如果 k=1，返回 1（当前节点就是第 k 层的节点，计数 1）
3. 否则，返回左子树第 k-1 层节点个数 + 右子树第 k-1 层节点个数（当前节点不是第 k 层，继续向下统计子树的第 k-1 层）

而且对左、右子树的统计，也完全遵循这个规则，直到遇到空节点或 k=1 才停止。

咱们以统计第 3 层节点个数为例，一步一步拆解整个过程：

步骤 1：从整棵树的根节点 1 开始，统计第 3 层节点个数

节点 1 不为空，k=3≠1，按照规则 3，需要统计左子树（以 2 为根的子树）的第 2 层节点个数、右子树（以 4 为根的子树）的第 2 层节点个数，然后求和。

子步骤 1.1：统计节点 2 所在左子树的第 2 层节点个数

节点 2 不为空，k=2≠1，按照规则 3，需要统计它的左子树（以 3 为根的子树）的第 1 层节点个数、右子树（空）的第 1 层节点个数，然后求和。

子步骤 1.1.1：统计节点 3 所在左子树的第 1 层节点个数

节点 3 不为空，k=1，按照规则 2，返回 1。所以节点 3 所在子树的第 1 层节点个数是 1。

子步骤 1.1.2：节点 2 的右子树为空，按照规则 1，返回 0。所以节点 2 所在左子树的第 2 层节点个数是 1 + 0 = 1。

步骤 2：统计节点 1 的右子树（以 4 为根的子树）的第 2 层节点个数

节点 4 不为空，k=2≠1，按照规则 3，需要统计它的左子树（以 5 为根的子树）的第 1 层节点个数、右子树（以 6 为根的子树）的第 1 层节点个数，然后求和。

子步骤 2.1：统计节点 5 所在左子树的第 1 层节点个数

节点 5 不为空，k=1，按照规则 2，返回 1。

子步骤 2.2：统计节点 6 所在右子树的第 1 层节点个数

节点 6 不为空，k=1，按照规则 2，返回 1。

所以节点 4 所在子树的第 2 层节点个数是 1 + 1 = 2。

步骤 3：整棵树的第 3 层节点个数

左子树第 2 层节点个数 1 + 右子树第 2 层节点个数 2 = 3，与我们手动计算的结果一致。

二、生活化例子："大楼楼层房间统计"

把二叉树想象成一栋大楼的结构，根节点是第 1 层（一楼大厅），每个节点代表一个房间，子节点代表下一层的房间。统计第 k 层节点个数就像是统计大楼第 k 层有多少个房间。

1. 节点对应的大楼结构明确

• 根节点 1：1 楼大厅（第 1 层）
• 左子树根 2：2 楼左侧走廊（第 2 层）
• 左子树的左子树 3：3 楼左侧房间（第 3 层）
• 右子树根 4：2 楼右侧走廊（第 2 层）
• 右子树的左子树 5：3 楼右侧左房间（第 3 层）
• 右子树的右子树 6：3 楼右侧右房间（第 3 层）

2. 统计第 3 层房间数量的流程（大楼管理员的工作）

第一步：管理员接到任务

大楼管理员接到任务："请统计我们这栋大楼第 3 层有多少个房间。"

管理员心想："第 3 层的房间都在第 2 层走廊的下面，我需要先去第 2 层，然后再往下一层就是第 3 层了。"

第二步：检查 2 楼左侧走廊

管理员来到 2 楼左侧走廊（节点 2），这里有一条向下的楼梯。管理员沿着楼梯下到下一层（k-1=2），发现这里有一个房间（节点 3）。管理员记录："2 楼左侧走廊下面有 1 个房间。"

第三步：检查 2 楼右侧走廊

管理员来到 2 楼右侧走廊（节点 4），这里有两条向下的楼梯。管理员先沿着左边的楼梯下到下一层，发现这里有一个房间（节点 5）。然后管理员沿着右边的楼梯下到下一层，发现这里也有一个房间（节点 6）。管理员记录："2 楼右侧走廊下面有 2 个房间。"

第四步：汇总统计结果

管理员汇总数据："2 楼左侧走廊下面 1 个房间 + 2 楼右侧走廊下面 2 个房间 = 3 个房间。所以第 3 层共有 3 个房间。"

这与我们树的第 3 层节点个数统计结果一致。

3. 统计二叉树第 k 层节点个数的本质："逐层深入"

从大楼房间统计的例子能看出来，统计二叉树第 k 层节点个数的逻辑是 "逐层深入"—— 每向下一层，k 值就减 1，直到 k=1 时开始计数。这种思想在很多实际场景中都有应用，比如：

• 公司组织架构中的 "层级员工统计"
• 文件系统中的 "特定深度文件统计"
• 网络拓扑中的 "特定跳数节点统计"

三、统计二叉树第 k 层节点个数的递归代码实现

统计二叉树第 k 层节点个数的代码逻辑清晰，基于 "空节点返回 0，k=1 返回 1，否则统计子树的 k-1 层" 的规则。咱们直接上代码，关键地方加了注释：

// 1. 先定义二叉树节点结构体（和之前一致）
typedef struct BinaryTreeNode {int data;                       // 节点存储的数据struct BinaryTreeNode* left;    // 指向左子节点的指针struct BinaryTreeNode* right;   // 指向右子节点的指针
} btn;  // 结构体别名，简化后续使用// 2. 统计二叉树第k层节点个数的函数：参数是当前子树的根节点和目标层数k，返回该子树第k层的节点个数
int countNodesAtLevelK(btn* root, int k) {// 规则1：如果当前节点是空，返回0（空树没有节点）if (root == NULL) {return 0;}// 规则2：如果k=1，返回1（当前节点就是第k层的节点）if (k == 1) {return 1;}// 规则3：否则，返回左子树第k-1层节点个数 + 右子树第k-1层节点个数return countNodesAtLevelK(root->left, k-1) + countNodesAtLevelK(root->right, k-1);
}

代码的核心就是逐层深入，每向下一层，k 值就减 1。比如咱们的示例树，调用 countNodesAtLevelK(root, 3)（root 指向节点 1），最终会返回 3，和我们手动计算的结果一致。

四、统计二叉树第 k 层节点个数的递归栈帧细节（彻底理解 "怎么跑的"）

为了彻底理解递归统计二叉树第 k 层节点个数的过程，我们还是以 countNodesAtLevelK(root, 3)（root 指向节点 1）为例，拆解每一步的栈状态、执行操作和返回结果。

核心概念：函数调用栈

递归的时候，每次调用 countNodesAtLevelK 函数，系统都会在 "函数栈" 里新增一个 "栈帧"—— 这个栈帧记录着当前函数的参数（比如 root 指向哪个节点，k 的值是多少）、局部变量以及 "下一步要执行的代码位置"（断点）。当函数执行到 return，这张 "便签" 就会被撕掉（栈帧弹出），程序回到上一张便签的 "断点位置" 继续执行。

1. 初始调用：countNodesAtLevelK(1, 3)（根节点 1，第 3 层）

• 栈状态（从上到下是最近调用的函数，栈帧里记录 "函数名 + root 值 + k 值 + 断点"）：[countNodesAtLevelK(1, 3)：root=1，k=3，断点在"计算左子树后"]
• 执行步骤：
  1. 检查 root=1 不为空，不触发规则 1。
  2. 检查 k=3≠1，不触发规则 2。
  3. 执行规则 3：计算左子树第 2 层节点个数→ 调用 countNodesAtLevelK(root->left, k-1)，也就是 countNodesAtLevelK(2, 2)（节点 1 的左子树是 2，k-1=2）。
  4. 栈帧变化：把 countNodesAtLevelK(1, 3) 的栈帧暂停（断点记在 " 计算完 countNodesAtLevelK(2, 2) 后，要计算右子树 "），新增 countNodesAtLevelK(2, 2) 的栈帧压入栈。此时栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(2, 2)：root=2，k=2，断点在"计算左子树后"]。
• 当前返回结果：无（还没到返回步骤）。

2. 执行 countNodesAtLevelK(2, 2)（节点 2，第 2 层）

• 栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(2, 2)：root=2，k=2，断点在"计算左子树后"]
• 执行步骤：
  1. 检查 root=2 不为空，不触发规则 1。
  2. 检查 k=2≠1，不触发规则 2。
  3. 执行规则 3：计算左子树第 1 层节点个数→ 调用 countNodesAtLevelK(root->left, k-1)，也就是 countNodesAtLevelK(3, 1)（节点 2 的左子树是 3，k-1=1）。
  4. 栈帧变化：暂停 countNodesAtLevelK(2, 2)（断点记在 " 计算完 countNodesAtLevelK(3, 1) 后，要计算右子树 "），新增 countNodesAtLevelK(3, 1) 的栈帧压入栈。此时栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(2, 2)（暂停）, countNodesAtLevelK(3, 1)：root=3，k=1]。
• 当前返回结果：无。

3. 执行 countNodesAtLevelK(3, 1)（节点 3，第 1 层）

• 栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(2, 2)（暂停）, countNodesAtLevelK(3, 1)：root=3，k=1]
• 执行步骤：
  1. 检查 root=3 不为空，不触发规则 1。
  2. 检查 k=1，触发规则 2，返回 1。
  3. 执行 return，撕掉 countNodesAtLevelK(3, 1) 的栈帧（弹出栈），回到 countNodesAtLevelK(2, 2) 的 "断点位置"—— 也就是 "计算完左子树后，准备计算右子树"。
• 当前返回结果：1（左子树第 1 层节点个数是 1）。

4. 回到 countNodesAtLevelK(2, 2)，继续执行

• 栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(2, 2)：root=2，k=2，断点在"计算左子树后"]
• 执行步骤：
  1. 执行规则 3：计算右子树第 1 层节点个数→ 调用 countNodesAtLevelK(root->right, k-1)，也就是 countNodesAtLevelK(NULL, 1)（节点 2 的右子树是空，k-1=1）。
  2. 栈帧变化：暂停 countNodesAtLevelK(2, 2)（断点记在 " 计算完 countNodesAtLevelK(NULL, 1) 后，要返回结果 "），新增 countNodesAtLevelK(NULL, 1) 的栈帧压入栈。此时栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(2, 2)（暂停）, countNodesAtLevelK(NULL, 1)：root=NULL，k=1]。
• 当前返回结果：1（左子树第 1 层节点个数是 1）。

5. 执行 countNodesAtLevelK(NULL, 1)（节点 2 的右子树，第 1 层）

• 栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(2, 2)（暂停）, countNodesAtLevelK(NULL, 1)：root=NULL，k=1]
• 执行步骤：
  1. 检查 root=NULL，触发规则 1，返回 0。
  2. 执行 return，撕掉 countNodesAtLevelK(NULL, 1) 的栈帧（弹出栈），回到 countNodesAtLevelK(2, 2) 的 "断点位置"—— 也就是 "计算完右子树后，准备返回结果"。
  3. countNodesAtLevelK(2, 2) 的左子树结果是 1，右子树结果是 0，所以返回 1 + 0 = 1。
  4. 执行 return，撕掉 countNodesAtLevelK(2, 2) 的栈帧（弹出栈），回到 countNodesAtLevelK(1, 3) 的 "断点位置"—— 也就是 "计算完左子树后，准备计算右子树"。
• 当前返回结果：1（左子树第 2 层节点个数是 1）。

6. 回到 countNodesAtLevelK(1, 3)，继续执行

• 栈状态：[countNodesAtLevelK(1, 3)：root=1，k=3，断点在"计算左子树后"]
• 执行步骤：
  1. 执行规则 3：计算右子树第 2 层节点个数→ 调用 countNodesAtLevelK(root->right, k-1)，也就是 countNodesAtLevelK(4, 2)（节点 1 的右子树是 4，k-1=2）。
  2. 栈帧变化：暂停 countNodesAtLevelK(1, 3)（断点记在 " 计算完 countNodesAtLevelK(4, 2) 后，要返回结果 "），新增 countNodesAtLevelK(4, 2) 的栈帧压入栈。此时栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(4, 2)：root=4，k=2，断点在"计算左子树后"]。
• 当前返回结果：1（左子树第 2 层节点个数是 1）。

7. 执行 countNodesAtLevelK(4, 2)（节点 4，第 2 层）

• 栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(4, 2)：root=4，k=2，断点在"计算左子树后"]
• 执行步骤：
  1. 检查 root=4 不为空，不触发规则 1。
  2. 检查 k=2≠1，不触发规则 2。
  3. 执行规则 3：计算左子树第 1 层节点个数→ 调用 countNodesAtLevelK(root->left, k-1)，也就是 countNodesAtLevelK(5, 1)（节点 4 的左子树是 5，k-1=1）。
  4. 栈帧变化：暂停 countNodesAtLevelK(4, 2)（断点记在 " 计算完 countNodesAtLevelK(5, 1) 后，要计算右子树 "），新增 countNodesAtLevelK(5, 1) 的栈帧压入栈。此时栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(4, 2)（暂停）, countNodesAtLevelK(5, 1)：root=5，k=1]。
• 当前返回结果：1（左子树第 2 层节点个数是 1）。

8. 执行 countNodesAtLevelK(5, 1)（节点 5，第 1 层）

• 栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(4, 2)（暂停）, countNodesAtLevelK(5, 1)：root=5，k=1]
• 执行步骤：
  1. 检查 root=5 不为空，不触发规则 1。
  2. 检查 k=1，触发规则 2，返回 1。
  3. 执行 return，撕掉 countNodesAtLevelK(5, 1) 的栈帧（弹出栈），回到 countNodesAtLevelK(4, 2) 的 "断点位置"—— 也就是 "计算完左子树后，准备计算右子树"。
• 当前返回结果：1（左子树第 1 层节点个数是 1）。

9. 回到 countNodesAtLevelK(4, 2)，继续执行

• 栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(4, 2)：root=4，k=2，断点在"计算左子树后"]
• 执行步骤：
  1. 执行规则 3：计算右子树第 1 层节点个数→ 调用 countNodesAtLevelK(root->right, k-1)，也就是 countNodesAtLevelK(6, 1)（节点 4 的右子树是 6，k-1=1）。
  2. 栈帧变化：暂停 countNodesAtLevelK(4, 2)（断点记在 " 计算完 countNodesAtLevelK(6, 1) 后，要返回结果 "），新增 countNodesAtLevelK(6, 1) 的栈帧压入栈。此时栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(4, 2)（暂停）, countNodesAtLevelK(6, 1)：root=6，k=1]。
• 当前返回结果：1（左子树第 1 层节点个数是 1）。

10. 执行 countNodesAtLevelK(6, 1)（节点 6，第 1 层）

• 栈状态：[countNodesAtLevelK(1, 3)（暂停）, countNodesAtLevelK(4, 2)（暂停）, countNodesAtLevelK(6, 1)：root=6，k=1]
• 执行步骤：
  1. 检查 root=6 不为空，不触发规则 1。
  2. 检查 k=1，触发规则 2，返回 1。
  3. 执行 return，撕掉 countNodesAtLevelK(6, 1) 的栈帧（弹出栈），回到 countNodesAtLevelK(4, 2) 的 "断点位置"—— 也就是 "计算完右子树后，准备返回结果"。
  4. countNodesAtLevelK(4, 2) 的左子树结果是 1，右子树结果是 1，所以返回 1 + 1 = 2。
  5. 执行 return，撕掉 countNodesAtLevelK(4, 2) 的栈帧（弹出栈），回到 countNodesAtLevelK(1, 3) 的 "断点位置"—— 也就是 "计算完右子树后，准备返回结果"。
• 当前返回结果：2（右子树第 2 层节点个数是 2）。

11. 回到 countNodesAtLevelK(1, 3)，继续执行

• 栈状态：[countNodesAtLevelK(1, 3)：root=1，k=3，断点在"计算右子树后"]
• 执行步骤：
  1. countNodesAtLevelK(1, 3) 的左子树结果是 1，右子树结果是 2，所以返回 1 + 2 = 3。
  2. 执行 return，撕掉 countNodesAtLevelK(1, 3) 的栈帧（弹出栈）。
• 当前返回结果：3。

12. 统计二叉树第 k 层节点个数结束

• 栈状态：空（所有栈帧都已弹出）
• 最终返回结果：3
• 核心统计逻辑：第 3 层节点个数 = 左子树第 2 层节点个数（1） + 右子树第 2 层节点个数（2） = 3

五、总结：统计二叉树第 k 层节点个数的核心要点

通过上面的详细拆解，我们可以总结出统计二叉树第 k 层节点个数的几个核心要点：

1. 统计规则：严格遵循 "空节点返回 0，k=1 返回 1，否则统计子树的 k-1 层"，这是递归统计的核心公式。

2. 层的定义：二叉树的第 1 层是根节点，第 2 层是根节点的子节点，以此类推。需要注意的是，有些定义中第 0 层是根节点，但我们这里采用第 1 层是根节点的定义。

3. 递归本质：利用二叉树的递归结构，将 "统计整棵树第 k 层" 拆成 "统计左子树第 k-1 层 + 统计右子树第 k-1 层"，每向下一层，k 值就减 1，直到 k=1 时开始计数。

4. 终止条件：遇到空节点返回 0，k=1 时返回 1，这两个条件共同确保递归能正常结束，避免无限循环。

5. 栈的作用：递归调用时，函数栈自动记录 "未完成的父节点计算" 和 "当前 k 值"，确保能正确地逐层深入和返回。

6. 时间复杂度：O (n)，其中 n 是树的节点个数，因为在最坏情况下（k 等于树的深度），每个节点都会被访问一次。

7. 空间复杂度：O (h)，其中 h 是树的高度，主要是递归调用栈的空间开销。在最坏情况下（单链树），h = n，空间复杂度为 O (n)；在最好情况下（完全二叉树），h = log n，空间复杂度为 O (log n)。

8. 应用场景：

   • 数据结构分析：评估树的各层分布情况
   • 算法优化：确定特定层的节点分布
   • 数据库索引：B 树、B + 树中的层统计
   • 人工智能：神经网络中的层分析

掌握了统计二叉树第 k 层节点个数的方法，你会发现它和之前的统计操作逻辑既有相似之处（都是递归拆解），又有自己的特点（逐层深入，k 值递减）。这种 "统一逻辑 + 差异化处理" 的特点，正是二叉树操作的精髓所在。记住：统计二叉树第 k 层节点个数的核心就是 "逐层深入，k=1 时计数"，这是解决很多二叉树层相关问题的基础。

下面是完整代码：

//求出二叉树第k层结点个数
int binarytreelevelksize(btn* root, int k)
{//我们依旧是使用递归//当节点为空时，就代表为0if (root == NULL){return 0;}//当节点不为空，且k==1//那就代表此时是到了相对于某一层的第一层//其实也就代表是到了我们要查找的第k层//比如一共5层，我们要找第3层//那么当k到了1的时候，就相当于是到了第3层//因为当k还为3的时候，此时是在第一层//而后k-1，此时k==2，代表向下移动1层，也就是到了第二层//接着再执行k-1，此时k==1，代表向下移动1层，也就是到了第三层//那么这个时候就得停止继续往下移动了//因为我们已经到了我们要查找的层数//并且，我们还得记录我们所到这一层的节点的数量//其实就是为1，因为我们此时是代表着移动到了这一层的某一个节点//可能是在左子树，也可能是在右子树，还有可能是根节点//但是都是一个节点，所以我们要返回1//那么这个时候自然就要返回回去了//但是在返回回去的同时，我们要进行加一//其实就是记录一下这里有个节点if (root != NULL && k == 1){return 1;}//其余的情况就是//返回左子树中，第k-1层的节点个数//加上//右子树中，第k-1层的节点个数//之所以要是k-1，是因为第k层，相对于第一层的左右子树来说//就是它们的第k-1层//话说有个 “二叉树家族”，辈分（层数）是这么排的：//老祖宗A是第 1 层，就他自己。//老祖宗生了俩孩子B和C，他俩是第 2 层。//B又生了个孩子D，C生了俩孩子E和F，这仨是第 3 层。//D还生了个孩子G，它是第 4 层。//现在家族要统计 “第 3 层有多少人”，就派你去数。你怎么数呢？//你先找到老祖宗A，问：“您这第 3 层有多少人啊？”//老祖宗A摸了摸胡子：“我这层是第 1 层，不是第 3 层。你得去问我儿子B和C，让他们数自己那一支的第 2 层有多少人，加起来就是家族第 3 层的人数啦～”//于是你找到B，问：“您那一支的第 2 层有多少人啊？”//B摆摆手：“我这层是第 2 层，但我是第 2 层的根啊，得问我儿子D和我那不存在的右孩子（因为B只有左孩子D），让他们数自己那一支的第 1 层有多少人，加起来就是我这一支第 2 层的人数～”//你又找到D，问：“您那一支的第 1 层有多少人啊？”//D一拍胸脯：“我就是第 1 层（相对于我爸B的子树来说），所以我这有 1 个人！”//至于B的右孩子（空的），它只能说：“我这没人，算 0。”//所以B那一支的第 2 层人数是1 + 0 = 1（就是D）。//接着你找到C，问：“您那一支的第 2 层有多少人啊？”//C点点头：“我得问我儿子E和F，让他们数自己那一支的第 1 层有多少人，加起来就是我这一支第 2 层的人数～”//你找到E，问：“您那一支的第 1 层有多少人啊？”//E说：“我就是，算 1！”你找到F，问：“您那一支的第 1 层有多少人啊？”//F说：“我就是，算 1！”所以C那一支的第 2 层人数是1 + 1 = 2（就是E和F）。//最后你汇总：B那支的 1 人 + C那支的 2 人 = 3 人。//这就是家族第 3 层的总人数（D、E、F）。//要是统计 “第 4 层有多少人”，流程也类似：//老祖宗让儿子们数第 3 层，儿子们让孙子们数第 2 层…… //最后会发现只有G这 1 个人～//你看，递归就是这样 “长辈把问题丢给晚辈，晚辈再丢给晚辈的晚辈，//最后把所有人的答案加起来” 的过程～//其实就是通过递归，去使程序移动到第k层，然后进行计数return binarytreelevelksize(root->left, k - 1) + binarytreelevelksize(root->right, k - 1);
}

这个函数的逻辑其实很清晰：如果当前节点为空，就返回 0；如果已经到了第 k 层（k=1），就返回 1；否则，就去左、右子树找第 k-1 层的节点。这样一层层往下找，直到找到第 k 层或者遇到空节点为止。

到了这里，本篇文章就又达到了40000多字，那么，我们暂时休息休息，将链式二叉树剩下的内容放在下一篇博客进行讲解。

结语：

当我们敲下 “统计第 k 层节点” 的最后一行代码，按下编译运行键，看着控制台跳出与预期完全一致的数字时 —— 或许是统计第 3 层时的 “3”，或许是统计第 2 层时的 “2”—— 我们总会下意识地停顿片刻。这一刻，屏幕上的数字不再只是一个冰冷的结果，而是这段关于链式二叉树学习旅程的缩影。从最初对着struct BinaryTreeNode结构体里的left和right指针发呆，反复琢磨 “这些零散的节点怎么才能像现实里的树一样，长出枝干、连成整体”，到如今能熟练地用递归思路拆解 “总节点统计”“叶子节点筛选”“树的深度计算”“第 k 层节点定位” 这四大核心问题，我们真正在代码里种下的，早已不是 “学会几个操作” 的表层技能，而是一套 “拆解复杂问题、串联核心逻辑” 的思维种子。

还记得第一次尝试写 “统计总节点个数” 函数时的手足无措吗？那时我们盯着屏幕上的二叉树示意图，总忍不住想 “从根节点开始，一个个往下数不就行了？” 于是提笔写下循环，试图用指针遍历每一个节点，却发现一旦遇到分叉（比如根节点既有左子树又有右子树），循环就会 “卡壳”—— 要么漏掉左子树的节点，要么重复统计右子树的节点。直到后来才猛然醒悟，树形结构的精髓从来不是 “线性遍历”，而是 “嵌套的子结构”——每一棵子树，本身就是一棵完整的树。就像一棵大树，它的左枝桠不是 “一段木头”，而是 “一棵小一点的树”；右枝桠也是如此，甚至枝桠上的每一片叶子，都可以看作 “只有一个节点的树”。

想通了这一点，“统计总节点” 的逻辑突然就清晰了：整棵树的节点数，不就是左子树的节点数、右子树的节点数，再加上当前这一个根节点吗？于是我们写下递归的终止条件 —— 如果节点为空（root == NULL），就返回 0，因为空树没有节点；然后递归调用左子树（countNodes(root->left)）和右子树（countNodes(root->right)），最后把两者的结果加 1（加上当前节点）。这段看似简单的代码return countNodes(root->left) + countNodes(root->right) + 1;，其实是 “分治思想” 在树形结构里的第一次具象化。就像面对一片茂密的森林，我们不再急于数清所有树木，而是先走到每一棵大树前，把它拆成 “左枝小树”“右枝小树” 和 “树干”，分别统计后再汇总 —— 这种 “化整为零” 的思路，从此成了我们解决树形问题的核心武器。

后来学习 “统计叶子节点”，我们又在这个基础上做了 “差异化调整”。叶子节点的定义是 “没有左子树也没有右子树的节点”，所以不能再像统计总节点那样 “只要非空就计数”，而是要给当前节点加一个精准的判断条件：只有当root->left == NULL && root->right == NULL时，才算是一个叶子节点，返回 1；如果不是叶子节点，就继续拆解左子树和右子树，汇总它们的叶子节点数。这个过程像极了在果园里筛选成熟的果实 —— 不是所有枝条都能结果，只有那些长在末梢、没有新枝芽的枝条，才挂着饱满的果子。我们在代码里写下的判断条件，就像是果农手里的筛选工具，精准地把 “叶子节点” 从众多节点里挑了出来。

有一次，我故意在一棵包含 5 层的二叉树里测试这个函数，手动数出叶子节点有 4 个，而代码返回的结果也是 4—— 那一刻的成就感，远不止 “代码跑通了” 那么简单。因为我知道，这段代码没有 “逐个遍历” 所有节点，而是通过 “分治递归”，自动找到了每一棵子树的叶子，再汇总起来。这就像给果树安装了自动采摘机，它不需要人工指引，就能顺着枝干找到末梢的果实 —— 这种 “让逻辑自己跑起来” 的感觉，正是编程的魅力所在。

再到 “计算树的深度”，逻辑又有了新的延伸。树的深度定义是 “从根节点到最远叶子节点的最长路径上的节点数”，所以核心不再是 “计数”，而是 “比较”。我们需要先算出左子树的深度，再算出右子树的深度，然后取两者中的最大值，最后加上当前这一层 —— 因为无论左子树和右子树哪一个更深，当前节点都是这条最长路径上的重要一环。比如一棵左子树深度为 3、右子树深度为 2 的二叉树，它的总深度就是 3+1=4，因为左子树的最长路径更长，而根节点是这条路径的起点。

这个逻辑让我想起建筑工人测量楼房高度的场景：要知道整栋楼的高度，不需要从一楼到顶楼逐阶攀爬、逐个计数，而是先测量每一层的高度，找到最高的那一段（比如中间有一层因为有阁楼，比其他层更高），再加上底层的基础高度。代码里的return max(leftDepth, rightDepth) + 1;，正是把这种 “找最长路径” 的现实逻辑，精准地转化成了可执行的代码指令。为了验证这个逻辑，我还特意画了一棵 “左深右浅” 的二叉树：根节点 1 的左子树是 2，2 的左子树是 3，3 的左子树是 4（左子树深度 3）；根节点 1 的右子树是 5，5 没有子节点（右子树深度 1）。手动计算总深度是 4，代码返回的结果也是 4—— 这一次，我不仅确认了逻辑的正确性，更感受到了 “代码与现实逻辑相通” 的奇妙。

而这次学习的 “统计第 k 层节点个数”，则是对 “分治递归” 思维的又一次深化。它不再是 “全局遍历统计”，而是 “精准定位到某一层”，这就要求我们让递归 “知道自己当前在第几层”，于是 “k 值递减” 的逻辑应运而生：父节点所在的层，比子节点所在的层高 1 层，所以父节点的第 k 层，就是子节点的第 k-1 层。当 k 减到 1 时，说明当前节点恰好就是目标层的节点，返回 1；如果节点为空，无论 k 是多少，都返回 0。

这个过程像极了快递员送包裹的场景：要把包裹送到某栋楼的 3 楼住户，快递员不需要在 1 楼就开始逐个敲门询问，而是先通过电梯到 2 楼 —— 因为 1 楼的 3 楼，对 2 楼来说就是 “下一层”（k-1=2）；到了 2 楼后，再找到通往 3 楼的楼梯，此时 k-1=1，刚好抵达目标楼层。代码里的return countLevelK(root->left, k-1) + countLevelK(root->right, k-1);，就是把 “逐层深入、精准定位” 的动作，转化成了递归的语言。为了彻底理解这个逻辑，我曾在纸上模拟过统计第 3 层节点的过程：

1. 根节点 1（第 1 层），k=3≠1，所以递归统计左子树 2 和右子树 4 的第 2 层节点；
2. 左子树 2（第 2 层），k=2≠1，递归统计左子树 3 和右子树（空）的第 1 层节点；
   • 左子树 3（第 3 层），k=1，返回 1；
   • 右子树（空），返回 0；
   • 左子树 2 的第 2 层节点数：1+0=1；
3. 右子树 4（第 2 层），k=2≠1，递归统计左子树 5 和右子树 6 的第 1 层节点；
   • 左子树 5（第 3 层），k=1，返回 1；
   • 右子树 6（第 3 层），k=1，返回 1；
   • 右子树 4 的第 2 层节点数：1+1=2；
4. 根节点 1 的第 3 层节点数：1+2=3，与实际节点 3、5、6 的数量一致。

当我在纸上画完这些步骤，看着数字一步步汇总成正确结果时，突然觉得 “递归” 不再是一个抽象的概念，而是一个 “有步骤、有方向” 的具体过程 —— 它就像一个不知疲倦的探索者，按照我们设定的规则，一层层深入，再把结果一层层带回来。

这四个操作看似各有不同，底层却共享着一套不变的逻辑框架：首先明确递归终止条件（空节点返回 0，这是所有树形递归的 “底线”）；然后根据需求处理当前节点（是计数、是比较，还是判断是否为目标层）；最后汇总子树的结果（左子树结果 + 右子树结果，或取两者的最大值）。就像用同一套积木，我们可以搭出 “统计总数” 的平房，也能搭出 “计算深度” 的高塔，还能搭出 “定位层级” 的楼阁 —— 而这套 “积木”，正是树形结构最核心的灵魂：分治思想。

更让人期待的是，今天我们在代码里写下的每一行，都在为未来的学习铺路。统计第 k 层时用到的 “逐层深入”，会成为我们理解 “层序遍历”（按层访问所有节点）的关键铺垫 —— 当我们学会了定位某一层，再扩展到遍历所有层，不过是多了一个 “从 1 到树的深度循环” 的步骤；计算树的深度时用到的 “子树比较”，更是判断 “平衡二叉树” 的核心基础 —— 平衡二叉树要求左子树和右子树的深度差不超过 1，本质上就是在 “计算深度” 的逻辑上多了一个 “差值判断”；甚至叶子节点的筛选逻辑，在实际应用中也有着重要作用：在决策树算法里，叶子节点对应着最终的决策结果（比如 “是否购买某件商品”“某个人是否有患病风险”），统计叶子节点数就是统计决策的类别数；在文件系统的目录树里，叶子节点代表着具体的文件（而非文件夹），筛选叶子节点就是查找所有非目录的文件；在 HTML 的 DOM 树里，叶子节点可能是文本节点或图片节点，定位叶子节点有助于精准修改页面内容。

或许此刻，你仍会对 “递归栈帧的变化” 感到些许模糊 —— 比如统计第 k 层时，递归调用栈是如何把 “root=1, k=3”“root=2, k=2”“root=3, k=1” 一层层压入，又如何在计算出结果后一层层弹出；也可能在 “k 值递减” 的逻辑里偶尔绕晕 —— 比如为什么根节点的第 3 层，到了左子树就变成了第 2 层，再到左子树的左子树就变成了第 1 层。但请一定不要着急，树形结构的理解本就不是 “一蹴而就” 的，它需要一个 “从模仿到熟练，从熟练到通透” 的过程。就像我们学骑自行车，刚开始总要盯着车轮害怕摔倒，双手紧握车把不敢放松，熟练后却能轻松掌控方向，甚至双手离把 —— 对于递归逻辑的理解，也是如此。

不妨试着做一些小实践：找一张白纸，画一棵包含 4 层、10 个节点的二叉树（比如根节点 1，第 2 层为 2 和 3，第 3 层为 4、5、6、7，第 4 层为 8、9、10），然后手动模拟一遍 “统计第 3 层节点个数” 和 “计算树的深度” 的过程。在模拟时，你可以用不同颜色的笔标注当前节点和 k 值（或当前子树的深度），看着这些标注一步步变化，你会清晰地看到递归是如何 “深入” 和 “返回” 的。

你也可以试着修改代码：比如在统计叶子节点的函数里，不再只返回个数，而是把所有叶子节点的值存入一个数组 —— 这就需要你在函数参数里增加一个数组指针和一个记录数组下标的变量，每找到一个叶子节点，就把它的值存入数组，并让下标加 1。这个小小的改动，会让你更深刻地理解 “如何在递归中传递和处理额外信息”，也会让你发现 —— 原来我们掌握的基础逻辑，能延伸出这么多新的可能。

再比如，你可以尝试写一个 “统计二叉树中偶数节点个数” 的函数。这个需求的核心逻辑，其实是在 “统计总节点” 的基础上，给当前节点加一个 “值是否为偶数” 的判断 —— 如果当前节点的值是偶数，就返回 “左子树偶数节点数 + 右子树偶数节点数 + 1”；如果不是偶数，就返回 “左子树偶数节点数 + 右子树偶数节点数”。当你写出这段代码并测试通过时，你会发现：只要掌握了 “分治递归” 的核心框架，无论需求如何变化，你都能快速找到修改方向。

下一次，我们会带着今天建立的 “分治思维”，继续探索链式二叉树的更多实用操作：如何查找树中某个特定值的节点（比如查找值为 5 的节点，返回它的地址）？如何销毁一棵二叉树以避免内存泄漏（因为链式结构的节点是动态分配的，不手动销毁会造成内存浪费）？这些问题看似更复杂，但本质上仍是 “拆解子树、处理当前节点、汇总结果” 的逻辑延伸。

比如 “查找特定值节点”，逻辑其实很简单：如果当前节点为空，返回 NULL（没找到）；如果当前节点的值等于目标值，返回当前节点的地址；如果不是，就先在左子树里找，如果左子树没找到，再在右子树里找 —— 这就是 “先左后右” 的查找逻辑。而 “销毁二叉树”，则需要注意销毁顺序：必须先销毁左子树，再销毁右子树，最后销毁当前节点 —— 因为如果先销毁当前节点，就会丢失左子树和右子树的地址，导致内存泄漏。这些逻辑看似细节满满，实则都是 “分治思想” 的具体应用。

相信那时你会更加深刻地体会到：当我们真正读懂了树形结构的 “生长逻辑”—— 每一棵子树都是完整的树，每一个节点都连接着左、右两个可能的世界 —— 再复杂的问题，也不过是枝干的再次组合。就像我们刚开始觉得 “统计第 k 层节点” 很难，学会后却发现它只是 “k 值递减” 的简单逻辑；未来面对 “平衡二叉树”“红黑树” 这些更复杂的树形结构时，我们也会发现，它们不过是在 “普通二叉树” 的基础上，增加了一些 “平衡规则” 或 “颜色规则”，核心的 “分治递归” 思维依然适用。

代码的世界里，每一段学习都是一次成长。从零散的节点到完整的树，从简单的遍历到复杂的统计，我们在代码里见证的，不仅是树形结构的生长，更是自己思维的生长。那些曾经让我们困惑的指针、递归和逻辑，最终都变成了我们手里的工具，帮助我们拆解更复杂的问题，探索更广阔的编程世界。

期待与你一起，在接下来的旅程里，继续解锁树形结构的更多奥秘，让每一行代码都生长出属于自己的力量 —— 因为我们知道，每一次敲击键盘，都是在为自己的思维搭建更坚实的 “枝干”；每一次调试成功，都是在为自己的知识 “挂上” 更饱满的 “果实”。