刷题感想之置换

这篇其实是之前下午讲课时用的

定义：

置换（Permutation）是一种将集合元素重新排列的函数，在密码学中经常用来实现加密操作。它是实

现加密操作的常客，像一把神奇的“排列钥匙”，能够打乱信息的原有顺序，让其变得难以被轻易解读。

置换是一个双射函数，将集合中的元素重新排列

先补充一下单射，满射和双射

单射：

对集合 A 中任意两个不同元素 a₁≠a₂，它们在 B 中的映射结果一定不同（A 中每个元素对应 B 中唯一元 素，B 中没有重复映射），可以简单理解为B集合范围大

满射：

集合 B 中的每一个元素，都能找到 A 中的至少一个元素与之对应

双射：

A 中每个元素对应 B 中唯一元素，且 B 中每个元素都有 A 中唯一元素对应

什么是置换呢？

类别：

置换有很多种顺序，简单的如恒等，顺时针，逆时针等。但是这里讲一些基础的

单置换：

举个例子：

集合{1,2,3}，定义置换 σ(1)=2,σ(2)=3,σ(3)=1

这个式子可以用轮换表示法 σ=(1 2 3)，圆括号表示循环。这是置换中一般的表示方法

计算方法可以表示为 1→2, 2→3, 3→1

可以用代码：

# 定义置换σ：用字典存储映射关系（键=原元素，值=置换后元素）
sigma = {1: 2, 2: 3, 3: 1}# 函数：应用置换到单个元素
def apply_sigma(x):if x not in sigma:raise ValueError(f"元素{x}不在置换定义域内（必须是1、2、3）")return sigma[x]# 测试单个元素的置换结果
print(apply_sigma(1))  
print(apply_sigma(2))  
print(apply_sigma(3)) 

这是三个元素都进行循环置换，还有一种是部分元素置换，部分元素不变

例如：

集合 {7,8,9} ，定义置换 ρ ： ρ(7)=8,ρ(8)=7,ρ(9)=9，

可以发现，第三个元素9仍未改变，就可以直观地表示为7↔8(9保持不变)，用双向箭头

用轮换表示法就是(78)(9)(而且这里的9是不变的，不变元素可省略，简记为(78))

# 定义置换τ：用字典存储映射关系
# 键=原元素（1,2,3），值=置换后元素（τ(1)=3, τ(3)=1, τ(2)=2）
tau = {1: 3, 3: 1, 2: 2}# 函数：对单个元素应用置换τ
def apply_tau(x):if x not in tau:raise ValueError(f"元素{x}不在置换定义域内（必须是1、2、3）")return tau[x]# 测试单个元素的置换结果
print(apply_tau(1))  
print(apply_tau(3))  
print(apply_tau(2))  

这是基础简便的置换，还有一个

复合置换：

复合置换是将两个或多个置换按顺序组合执行的操作，核心规则是「从右到左执行」—— 先应用右侧的 置换，再将结果代入左侧的置换，最终形成一个新的置换。

比如说定义两个基础置换a=(1,2,3)，b=(1,3)(2)如果将这两个置换合并为一个置换，假设a∘b=a(b(x))，根 据复合置换的先后顺序：

第1个元素，先算b(1)=3 ，再算a(3)=1 → 最终a∘b(1)=1

第2个元素，先算b(2)=2 ，再算a(2)=3 → 最终a∘b(2)=3

第3个元素：先算b(3)=1 ，再算a(1)=2 → 最终a∘b(3)=2

映射关系：a∘b(1)=1 ，a∘b(2)=3 ，a∘b(3)=2

轮换表示：(2,3)(1) ，简记为 (2,3)

直观映射：2↔3 （1 保持不变）

一个比较麻烦的例子，对于元素{1,2,3,4,5}

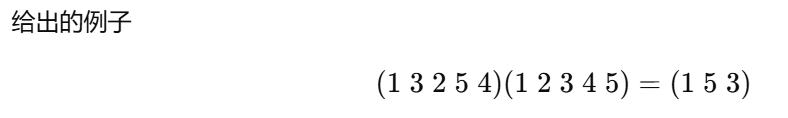
根据置换规则，右侧置换先执行1→2 ， 2→3 ， 3→4 ， 4→5 ， 5→1

左侧置换1→3 ， 3→2 ， 2→5 ， 5→4 ， 4→1

对每个元素整理，1→5 ， 5→3 ， 3→1 ； 2→2 ， 4→4，则1→5→3→1，(1,5,3),不变元素可忽略

复合置换的执行有前提：

定义域 / 值域相同（反例最常见）：

置换 σ ：作用于集合 {1,2,3} ， σ(1)=2 ， σ(2)=3 ， σ(3)=1

置换 τ ：作用于集合 {3,4,5} ， τ(3)=4 ， τ(4)=5 ， τ(5)=3

复合尝试：计算 σ∘τ(3) → 先 τ(3)=4 ，但 σ 的定义域是 {1,2,3} ，没有 4 的映射定义，无法继续算，复合失败。

通俗的讲，两个置换的集合不同，“右置换输出（4）” 不在 “左置换的输入范围（1-3）” 内，衔接断裂。

元素范围没有冲突：

置换 σ ：作用于 {A,B,C,D} ， σ(A)=B ， σ(B)=A ， σ(C)=D ， σ(D)=C （轮换表示： (AB)(CD) ）

置换 τ ：作用于 {A,B,C}， τ(A)=C ， τ(C)=A ， τ(B)=B

复合尝试：计算 σ∘τ(D) → τ 的定义域没有 D，无法先对 D 执行 τ 映射，复合失败。

问题：元素 D 在 σ 中存在，但在 τ 中无定义，无法完成 “先 τ 后 σ ” 的完整流程

参与复合的是双射（最基本的）：

函数 f （不是置换，非双射）：作用于 {1,2,3} ， f(1)=2 ， f(2)=2 ， f(3)=1 （非单射：1 和 2 都映射到 2）

置换 σ ：作用于 {1,2,3} ， σ(1)=2 ， σ(2)=3 ， σ(3)=1

复合尝试：计算 σ∘f(1)=σ(2)=3 ， σ∘f(2)=σ(2)=3 → 最终映射 1→3、2→3，出现 “多对一”，不再是置换（置换必须是双射），复合无意义。

核心问题： f 不是双射，导致复合结果失去置换的本质属性，无法形成有效的复合置换。这个其实就不 必多讲了，在开头提到置换的定义的时候就提到过

逆置换：

就是把置换反过来，也可以直接把箭头给反过来即可

# 原置换：1→2，2→3，3→1
p = {1:2, 2:3, 3:1}# 逆置换（键值互换）
p_inv = {v:k for k,v in p.items()}# 应用逆置换的简单函数
def inv(x):return p_inv[x]# 测试逆置换
print(inv(2))  # 1（对应原置换1→2的逆）
print(inv(3))  # 2（对应原置换2→3的逆）
print(inv(1))  # 3（对应原置换3→1的逆）

以具体的题目为例子，new star CTF2025 置换：

打开

前面给的例子之前就提到过，直接解析题。

记P1=(1 3 5 7)(2 4 6)(8 10 12 14)

P2=(1 2 3 4 5 6 7)(8 9 10 11 12 13 14)

根据复合置换规则，先P1，后P2,先分别得出

P1映射表

1→3,2→4,3→5,4→6,5→7,6→2,7→1,8→10,9→9,10→12,11→11,12→14,13→13,14→8.

P2映射表

1→2,2→3,3→4,4→5,5→6,6→7,7→1,8→9,9→10,10→11,11→12,12→13,13→14,14→8.

由此得出F映射

1→4,2→5,3→6,4→7,5→1,6→3,7→2,8→11,9→10,10→13,11→12,12→8,13→14,14→9

得到F=(1 4 7 2 5)(3 6)(8 11 12)(9 10 13 14)

根据这个例子及规则，这就是要求其逆置换

根据求出来的F，这个是不相交的，求逆置换可以相当于把箭头反过来（不相交就是两个置换间没有共同元素，从而两个置换不能构成复合置换）

则最终得到的是：

1→5,2→7,3→6,4→1,5→2,6→3,7→4,8→12,9→14,10→9,11→8,12→11,13→10,14→13.

将数字对应字母：

A -> E，B -> G，C -> F，D -> A，E -> B，F -> C，G -> D，H -> L，I -> N，J -> I，K -> H，L -> K，M -> J，N -> M

其它的不变。根据密文，得到置换后的结果  

SUCH A SIMPLE PERMUTATION WILL DEFINITELY NOT STUMP YOU.

这个就是答案，只是大小写的问题

应用：

置换在加密算法中的应用很广泛，包括RC4，AES，DES等，以RC4为例：

在第一，第二阶段都有

密钥调度算法(KSA)阶段：用密钥初始化 S 盒的置换

在初始化S盒后，通过置换，使 S 状态与密钥强关联且具有伪随机性

用密钥填充一个临时数组 K（密钥长度不足 256 则循环填充）

for i in range(256):
# 用密钥计算置换索引 j，完成 S 盒的首次置换
j = (j + S[i] + key[i % key_len]) % 256
S[i], S[j] = S[j], S[i] # 交换（置换核心操作）

举个简单的例子，以四元素S盒为例

[0,1,2,3]，密钥为[1,2]

i=0：j = (0 + S[0] + K[0]) % 4 = (0 + 0 + 1) %4 =1 → 交换 S[0] 和 S[1] → S 变为 [1, 0, 2, 3]

i=1：j = (1 + S[1] + K[1]) %4 = (1 + 0 + 2) %4 =3 → 交换 S[1] 和 S[3] → S 变为 [1, 3, 2, 0]

i=2：j = (3 + S[2] + K[2]) %4 = (3 + 2 + 1) %4 =6%4=2 → 交换 S[2] 和 S[2]（不变）→ S 仍为 [1, 3, 2,

0]。

i=3：j = (2 + S[3] + K[3]) %4 = (2 + 0 + 2) %4=4%4=0 → 交换 S[3] 和 S[0] → S 变为 [0, 3, 2, 1]。

伪随机数生成算法（PRGA）：动态置换生成密钥流：

i = j = 0
while True:
i = (i + 1) % 256
j = (j + S[i]) % 256
S[i], S[j] = S[j], S[i] # 动态置换 S 盒
t = (S[i] + S[j]) % 256
yield S[t] # 生成密钥流字节

每次生成密钥流前，S 都会被置换（交换 S[i] 和 S[j]）

用AI生成一个简单的RC4算法代码：

def rc4_key_schedule(key):
S = list(range(256)) # 初始 S 盒：[0,1,...,255]
j = 0
key_len = len(key)
for i in range(256):
# 用密钥计算置换索引 j，完成 S 盒的首次置换
j = (j + S[i] + key[i % key_len]) % 256
S[i], S[j] = S[j], S[i] # 交换（置换核心操作）
return S
def rc4_prga(S):
i = j = 0
while True:
i = (i + 1) % 256
j = (j + S[i]) % 256
S[i], S[j] = S[j], S[i] # 动态置换 S 盒
t = (S[i] + S[j]) % 256
yield S[t] # 生成密钥流字节
# 示例：用密钥 b"key" 初始化并生成密钥流
key = b"key"
S = rc4_key_schedule(key)
keystream = rc4_prga(S)
# 前 5 个密钥流字节（每次调用 next 都会触发 S 盒置换）
print([next(keystream) for _ in range(5)])

这里就不再过多讲述了，重点是置换思想。像前面提到的恒等，顺时针，逆时针置换道理一样，只是方法不同