2019年JCP SCI1区TOP，改进蚁群算法+多车场多目标绿色车辆路径规划，深度解析+性能实测

---

1.摘要

车辆路径问题（VRP）是运输科学中的重要研究方向，因其能够为物资配送中的组织带来显著的成本节约和服务提升机会。论文提出了一种多仓库绿色车辆路径问题（MDGVRP），该问题通过最大化收入并最小化成本、时间和排放来优化物流路径。为了解决这一问题，论文采用了一种改进蚁群优化算法（IACO），IACO算法通过创新的挥发信息更新机制，显著提高了解决方案的质量。实验结果表明，与传统的蚁群算法相比，IACO在解决MDGVRP时能够获得更优的解，并展示了较好的响应性和简洁性，适用于多目标优化问题的求解。

2.问题描述

多仓库绿色车辆路径问题（MDGVRP）在优化物资配送过程中车辆的行驶路线，以最大化收入、最小化成本、行驶时间和排放。研究采用了图论中的路由模型，将客户作为节点，通信路径作为边，构建了一个包含多个仓库和配送中心的运输网络。模型考虑了车辆容量限制，并将问题分为四个目标：收入最大化、成本最小化、行驶时间最小化和减少CO2排放。模型在多个目标下进行优化，使用了多种约束条件，包括每辆车的容量限制、每个客户仅接受一次配送、车辆从仓库出发且无法转移到其他仓库等。

收益最大化：
$$\max Z_1=\sum _S\sum _{j\in N}Flo{w}_{sj}.Price.x_{sj}$$

成本最小化:
$$\begin{array}{rl}\min Z_2& =\sum _S\sum _{j\in N}Flo{w}_{sj}.Tran{s}_{sj}.x_{sj}+\sum _{i\in N}\sum _{S}Tran{s}_{is}.x_{is}\\ & +\sum _{(i,j)\in A}Flo{w}_{ij}.Tran{s}_{ij}.x_{ij}\end{array}$$

耗费时间最小化：
$$\begin{array}{rl}\min Z_2& =\sum _S\sum _{j\in N}Flo{w}_{sj}.Tran{s}_{sj}.x_{sj}+\sum _{i\in N}\sum _{S}Tran{s}_{is}.x_{is}\\ & +\sum _{(i,j)\in A}Flo{w}_{ij}.Tran{s}_{ij}.x_{ij}\end{array}$$

污染最小化：
$$\begin{array}{rl}\min Z_4& =Poll.\left[\sum _S\sum _{j\in N}Dis{t}_{sj}.x_{sj}+\sum _{(i,j)\in A}Dis{t}_{ij}.x_{ij}\right]\\ & +\sum _{i\in N}\sum _{S}Dis{t}_{is}.x_{is}\end{array}$$

3.改进蚁群算法

改进蚁群算法通过更新信息素矩阵和启发式信息，避免蚂蚁过早收敛到最优路径。信息素蒸发机制用于逐步减少较差解的信息素浓度，而对于较优解，则增加信息素量。通过概率矩阵和累积概率矩阵的选择，车辆根据需求逐步服务客户，直到满足所有需求或容量达到上限。

为了更新信息素，采用蚁群权重策略：
$$\Delta {\tau }^{\mathrm{w}}=\{\begin{array}{llcc}\frac{Q}{\mathrm{global}-\mathrm{best}(\mathrm{It})}& ,\text{if allocation is done by ant w}& & \\ 0& ,& otherwise& \end{array}$$

其中，$Q$表示信息素蒸发率，$Globa{l}_{best}$表示蚂蚁$w$在上次迭代中找到的最佳解的总成本。信息素更新的目标是减少较差解的信息素浓度，并增加最佳解的信息素浓度。算法通过计算概率矩阵并选择随机数来确定仓库和首个客户。一旦车辆满足第一个需求，若容量已满或无法接受新请求，则返回仓库并结束路径；否则，继续计算新的概率矩阵并服务下一个客户。

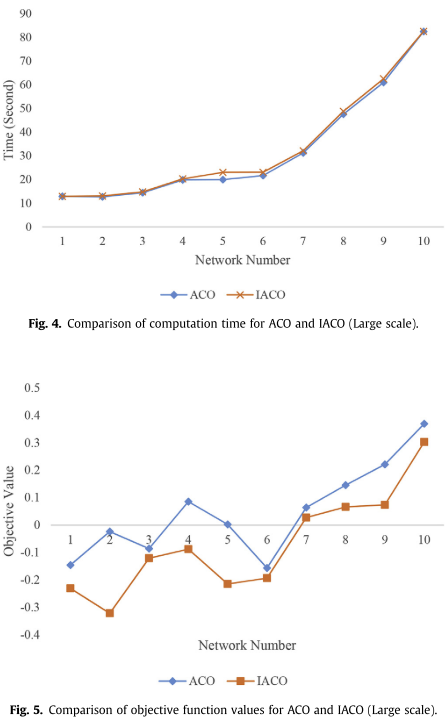
4.结果展示

5.参考文献

[1] Li Y, Soleimani H, Zohal M. An improved ant colony optimization algorithm for the multi-depot green vehicle routing problem with multiple objectives[J]. Journal of cleaner production, 2019, 227: 1161-1172.

6.代码获取

xx

7.算法辅导·应用定制·读者交流

xx