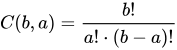【模板】组合数（牛客）

写在前面：

牛客每日一题持续更新中！

今天给亦菲彦祖们带来的是 【模板】组合数

题目如下：

题目描述

给定两个整数 a和 b，请你计算组合数 的值，并对模数 取模。

输入:

• 第一行输入一个整数 T，表示测试用例数量。
• 接下来 T 行，每行输入两个整数 。

输出:

• 对于每个测试用例，在一行上输出  的值。

解题思路

这是一个典型的求解组合数模质数的问题。由于有多组查询，使用预处理的方法效率最高。

• 组合数公式

  • 组合数 （在本题中是 ）的计算公式为：
  • 在模运算中，除法不能直接计算，需要转化为乘以除数的 模逆元。
• 模逆元

              非零实数 𝑎 ∈𝐑 的乘法逆元就是它的倒数 𝑎−1。类似地，数论中也可以定义一个                  整数 𝑎 在模 𝑚 意义下的逆元 𝑎−1mod𝑚，或简单地记作 𝑎−1。这就是 模逆元。

               a^p-1=1(modp) = a^p-2 * a = 1(mod p) 所以a^p-2 = 1/a(mod p)

                所以根据逆元我们可以将 1/a 转化为 a^p-2 (mod p) 理论成立 实践开始

1. 预处理

   • 由于 500000 的最大值可达500000! ，我们可以预先计算出从 0! 到 500000! 的阶乘值及其模逆元，并将它们存储在数组中。这样每次查询时就可以直接使用，达到 O(1) 的查询效率。
   • 预处理阶乘数组 fact: fact[i] = i! % MOD。
   • 预处理阶乘的逆元数组 invFact: invFact[i] = (i!)^-1 % MOD。
     • 直接对每个阶乘求逆元效率较低（）。
     • 更高效的方法是：先用快速幂求出最大阶乘 fact[N] 的逆元 invFact[N]。
     • 然后利用递推关系 invFact[i-1] = invFact[i] * i % MOD，从后向前计算出所有阶乘的逆元。这样总的预处理时间复杂度接近 。
     • 稍微需要注意一下invFact数组的计算 因为他是逆元分母 它的计算有点抽象 我们是先求出invFact[Maxn]即 1/Maxn! ，它的上一位 invFact[Maxn-1]，  即 1/(Maxn-1)! = 1/Maxn! *Maxn = invFact[Maxn] * Maxn so..

2. 计算组合数

   • 有了预处理的数组，计算组合数就变得非常简单：  
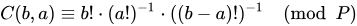
   • 如果 a>b，则组合数为0。

代码实现：

C/C++版本：

#include <iostream>
#include <vector>using namespace std;
using LL = long long;const int MOD = 1e9 + 7;        // 模数
const int MAXN = 500000;        // 最大可能的值LL fact[MAXN + 1];             // 存储阶乘 fact[i] = i! mod MOD
LL invFact[MAXN + 1];          // 存储阶乘的逆元 invFact[i] = 1/(i!) mod MOD// 快速幂算法：计算 base^exp mod MOD
LL power(LL base, LL exp) {LL res = 1;base %= MOD;while (exp > 0) {if (exp % 2 == 1) res = (res * base) % MOD;  // 如果指数是奇数，乘上当前的basebase = (base * base) % MOD;                  // 平方baseexp /= 2;                                   // 指数减半}return res;
}// 预处理阶乘和逆阶乘
void precompute() {fact[0] = 1;      // 0! = 1invFact[0] = 1;   // 1/0! = 1// 正向计算阶乘：fact[i] = fact[i-1] * ifor (int i = 1; i <= MAXN; i++) {fact[i] = (fact[i - 1] * i) % MOD;}// 计算最大阶乘的逆元invFact[MAXN] = power(fact[MAXN], MOD - 2);// 逆向计算逆阶乘：利用递推关系 invFact[i] = invFact[i+1] * (i+1)for (int i = MAXN - 1; i >= 1; i--) {invFact[i] = (invFact[i + 1] * (i + 1)) % MOD;}
}// 计算组合数 C(b, a) = b! / (a! * (b-a)!)
LL combinations(int b, int a) {if (a < 0 || a > b) {  // 边界检查return 0;}// C(b, a) = fact[b] * invFact[a] * invFact[b-a] mod MODreturn (((fact[b] * invFact[a]) % MOD) * invFact[b - a]) % MOD;
}// 处理每个测试用例
void solve() {int a, b;cin >> a >> b;cout << combinations(b, a) << '\n';  // 注意参数顺序：combinations(b, a) 对应 C(b, a)
}int main() {ios::sync_with_stdio(false);  // 加速C++输入输出cin.tie(0);                   // 解除cin和cout的绑定precompute();                 // 预处理阶乘和逆阶乘int t;cin >> t;while (t--) {solve();                  // 处理每个测试用例}return 0;
}

Python版本：

MOD = 10**9 + 7
MAXN = 500000# 预计算阶乘和逆阶乘
fact = [1] * (MAXN + 1)
inv_fact = [1] * (MAXN + 1)def power(base, exp):"""快速幂算法：计算 base^exp mod MOD"""res = 1base %= MODwhile exp > 0:if exp % 2 == 1:res = (res * base) % MODbase = (base * base) % MODexp //= 2return resdef precompute():"""预处理阶乘和逆阶乘"""# 计算阶乘for i in range(1, MAXN + 1):fact[i] = (fact[i - 1] * i) % MOD# 计算最大阶乘的逆元inv_fact[MAXN] = power(fact[MAXN], MOD - 2)# 逆向计算逆阶乘for i in range(MAXN - 1, 0, -1):inv_fact[i] = (inv_fact[i + 1] * (i + 1)) % MODdef combinations(b, a):"""计算组合数 C(b, a) = b! / (a! * (b-a)!) mod MOD"""if a < 0 or a > b:return 0return (fact[b] * inv_fact[a] % MOD) * inv_fact[b - a] % MODdef main():import sysinput = sys.stdin.readdata = input().split()precompute()  # 预处理t = int(data[0])idx = 1results = []for _ in range(t):a = int(data[idx]); b = int(data[idx + 1])idx += 2results.append(str(combinations(b, a)))  # 注意参数顺序print("\n".join(results))if __name__ == "__main__":main()

Java版本：

import java.io.*;
import java.util.*;public class CombinationCalculator {static final int MOD = 1000000007;static final int MAXN = 500000;static long[] fact = new long[MAXN + 1];static long[] invFact = new long[MAXN + 1];// 快速幂算法static long power(long base, long exp) {long res = 1;base %= MOD;while (exp > 0) {if ((exp & 1) == 1) {res = (res * base) % MOD;}base = (base * base) % MOD;exp >>= 1;}return res;}// 预处理阶乘和逆阶乘static void precompute() {fact[0] = 1;invFact[0] = 1;// 计算阶乘for (int i = 1; i <= MAXN; i++) {fact[i] = (fact[i - 1] * i) % MOD;}// 计算最大阶乘的逆元invFact[MAXN] = power(fact[MAXN], MOD - 2);// 逆向计算逆阶乘for (int i = MAXN - 1; i >= 1; i--) {invFact[i] = (invFact[i + 1] * (i + 1)) % MOD;}}// 计算组合数 C(b, a)static long combinations(int b, int a) {if (a < 0 || a > b) {return 0;}return (((fact[b] * invFact[a]) % MOD) * invFact[b - a]) % MOD;}public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));precompute();  // 预处理int t = Integer.parseInt(br.readLine());while (t-- > 0) {String[] input = br.readLine().split(" ");int a = Integer.parseInt(input[0]);int b = Integer.parseInt(input[1]);bw.write(combinations(b, a) + "\n");  // 注意参数顺序}bw.flush();bw.close();br.close();}
}

算法及复杂度

• 算法：组合数学、费马小定理、快速幂、预处理
• 时间复杂度：预处理 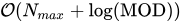，其中 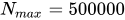。每个测试用例的查询为 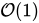。总时间复杂度为 。
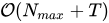• 空间复杂度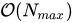：，用于存储阶乘和阶乘逆元的数组。

好了，各位码友，代码已经调试通过，文章也已commit，就等各位的push了。点赞不要 //TODO，关注务必 star！

写在后面：