二分查找算法+题目详解
目录
1.二分查找
2.在排序数组中查找元素的第一个和最后一个位置
3.x的平方根
4.搜索插入位置
5.山脉数组的峰顶索引
6.寻找峰值
7.点名
二分查找是一个非常基础的查找算法,但是效率却是十分的高效,既然又简单又高效,就说明他十分的‘恶心’,今天我们就来探索这个最‘恶心’的算法吧.
二分查找很多人认为只有在有序的情况下才可以用,但是其实只要满足‘二段性’就可以利用二分算法来解决题目,那么什么是‘二段性’呢? 所谓的二段性就是指当我们找到一个位置时,可以将数组分为左右两部分,根据判断条件判断,如果可以舍去其中一部分,只留下另一部分,我们将这种性质叫做‘二段性’
算法模板:
一般二分算法模板:
while(left <=right)
{mid = left+(right - left)/2;if(......)left = mid + 1;else if(.....)right = mid - 1;elsereturn mid; {求最左值的算法模板:
while(left < right){ int mid = left +(right - left)/2;if(......) left = mid+1;else right = mid ;
}
求最右值的算法模板:
while(left < right)
{int mid = left + (right-left+1)/2;if(......) right = mid-1;else left = mid;
}1.二分查找
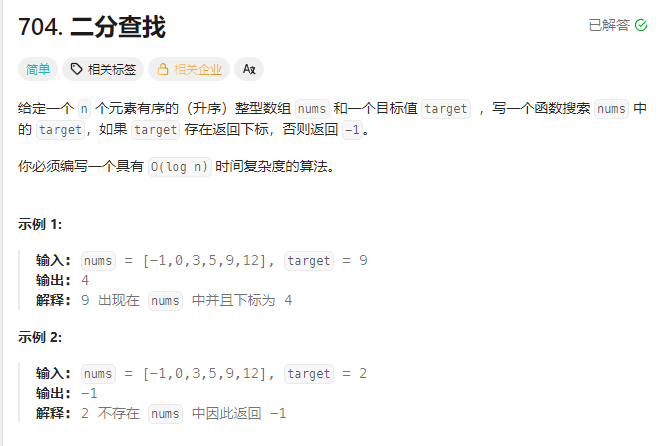
解题思路:这道题目的看题目就知道是利用二分查找算法来解决,所以我们直接开始我们的二分查找算法。详细代码解释在代码示例中展示
代码示例:
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0,right = nums.size()-1;//确定数组的左右边界while(left<=right) // 循环条件,只要当left>right之后结束查找{int mid = left + (right - left)/2;//寻找中间下标,这种求法可以防止由于left和right都接 //进int的极限值导致结果溢出if(nums[mid]==target)//如果和目标值相等说明找到了该位置,返回下标即可return mid;else if(nums[mid] < target)// 如果小于目标值,由于是有序数组,所以只需要将left的值改为中 //间值的右边一个即可left = mid+1;else // 如果大于目标值,由于是有序数组,所以只需要将right的值改为 //中间值的左边一个即可right = mid -1; }return -1;//运行到这里说明找不到目标元素}
};这道题目是最典型的一般二分查找算法题,我们直接运用模板就可以解决,因为它符合我们二分算法的前提——‘二段性’,当我们求mid时,可以根据mid的位置的数据大小来判断放弃其中那一部分,留下那一部分。
2.在排序数组中查找元素的第一个和最后一个位置

题目解析:
该题目的意思是要求我们在一个非递减顺序排列的数组中找到目标值target首次出现的位置和最后一次出现的位置,如果数组中没有该目标值则首尾位置都返回-1,同时如果是空数组首尾位置也都返回-1.
解题思路:
这道题目的暴力解法可以用便利数组来记录首尾位置,但是时间复杂度太高,题目要求时间复杂度为O(logn),所以我们选择二分算法,来寻找最左值和最右值。详细解释在代码示例中
代码示例:
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int left = 0,right = nums.size()-1; //left和right分别用来记录最左和最右的位置if(nums.size() == 0) //处理nums为空的情况return {-1,-1};// 寻找最左值while(left < right) //先看循环里面的内容再来仔细看循环条件的解释, 当left=right的时 //候,我们找到了一个最终的位置,只需要判断他们俩相等的时候是否和target相同即可{ int mid = left +(right - left)/2;//这里必须用这种求中点的方法,根据我们更新left和 // right的条件,这里的求中点如果不用left +(right - left)/2去用 left + (right- // left+1)/2,当nums[mid]>=target时,当只剩最后两个元素时,mid会一直等于第二个 //元素,出现死循环if(nums[mid]<target) left = mid+1;//如果nums[mid]小于目标值,说明此时mid所在的位置 //一定是不符合要求,所以我们可以丢掉mid的左半边 //将left改为mid+1,更新区间.else right = mid ;// 这里是当nums[mid]>=target的情况,当前位置等于target的时候, //我们没办法去确定这是不是最左值,所以我们只能将大于和等于两种情 //况合并,right变为mid不断所以区间来寻找最左值。}int begin = -1; //返回的起始位置if(nums[left] != target) return {-1,-1};//如果left和right相等的时候和target不相等, //说明数组中不存在targetelse begin = left;//将最左值更新;// 寻找最右值right = nums.size() -1;while(left < right)// 与求最左值的理由相同{int mid = left + (right-left+1)/2; //这里必须用这种求中点的方法,根据我们更新left和right的条件,这里的求中点如果不用left +(right - left+1)/2 去用 left + (right-left)/2,当nums[mid]<=target时,当只剩最后两个元素时,mid会一直等于第一个元素,出现死循环if(nums[mid] >target) right = mid-1;//如果nums[mid]大于目标值,说明此时mid所在 //的位置一定是不符合要求,所以我们可以丢掉//mid的右半边将right改为mid-1,更新区间.else left = mid;// 这里是当nums[mid]<=target的情况,当前位置等于target的时候, //我们没办法去确定这是不是最右值,所以我们只能将小于和等于两种情 //况合并,left变为mid不断所以区间来寻找最右值。}//有了最左值就一定右最右值,直接返回即可return {begin,right};}
};3.x的平方根

题目解析:
题目要求我们求出一个非负整数的x的平方根,我们只需要这个平方根的整数部分,也就是向下取整,所以我们所求的整数是小于等于x的算术平方根的。
解题思路:
可以用暴力解法去遍历1~x中间的所有数来求出答案,我们这里用二分查找来实现
class Solution {
public:int mySqrt(int x) {long long left = 0,right = x; //定义long long是为了防止数据溢出 left指向最左,right指向最右while(left<right){long long mid = left +(right -left+1)/2; //我们思考,当我们求出一个mid的值作为中间值时,我们可以判断mid的平方是否是满足要求的,如果mid的平方//是大于我们的x的,说明此时的mid落在的我们正确答案的右边,而且mid的右边不可能存在正确答案,所以我
//们就可以舍去右边,这就是符合我们所说的‘二段性’的,所以我们才可以用二分查找算法。那么我们此时的
//mid的平方是大于x的,所以我们要去mid的左边寻找答案,所以right就要更新为mid-1if(mid*mid > x) right = mid -1;//如果当mid的平方是小于等于x的,此时我们的mid可能是正确,也可能不是,所以我们不断缩小区间,让left
//不断的更新为mid,这里不是让left更新为mid是因为我们的答案有可能是小于x的平方根的,所以我们不敢断定
//此时的mid就一定不是正确答案,只有当left=right的时候,此时的值,才一定可以保证是正确答案。else left = mid; }return left;}
};4.搜索插入位置
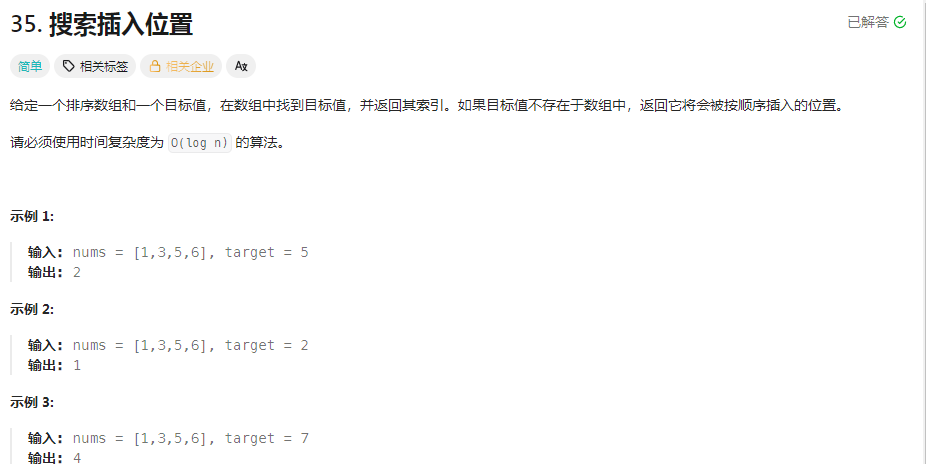
题目解析:
本道题很直接明了的告诉了我们目标就是将一个target值插入一个数组中,并且让他依旧是有序数组,所以我们只需要找到比target值大的值中的那个最小值,所以我们依旧二分算法;
解题思路:
我们只需要通过二分算法,寻找比target值大的那个值就可以了,符合我们的二分算法
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0,right = nums.size();//二分算法的老样子开头while(left < right ){int mid = left+(right - left)/2;if(nums[mid] >= target) right = mid; //当我们的nums[mid]的值大于等于target的时
候,我们这时mid有可能是正确答案,也有可能不是,我们要找比target大一点的值,所以我们只能让right = mid,而不能是right = mid+1;如果加一就有可能越过正确值//当我们的nums[mid]的值<target的时候,我们这时mid的左侧绝对不可能有正确答案,所以去mid的右侧寻找就可以。else left = mid +1;}
//跳出循环和就找到了那个值,返回其下表即可return left;}
};5.山脉数组的峰顶索引

题目解析:
改题目的意思就是要我们求一个数组里面的最大值的索引位置,并且给定的数组是按照先递增在递减的顺序的。
解题思路:
这道题目还是很显然的说出了要时间O(log(n))的时间复杂度,所以很容易想到二分的解法,所以我们用二分查找来解决这道问题.
代码示例:
class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int left =0 ,right = arr.size()-1;while(left < right){int mid = left+(right - left)/2; //当我们的找到的mid所对应的值大于mid+1对应的值时,我们可以发现mid可能是返回值,所 //以下一步的缩小区域就只能让right等于midif(arr[mid] > arr[mid +1]) right = mid;//当mid所对应的值小于mid+1对应的值时,此时mid不可能是要求的返回值,所以我们可以让 //left = mid+1;else left = mid +1;}return left;}
};6.寻找峰值
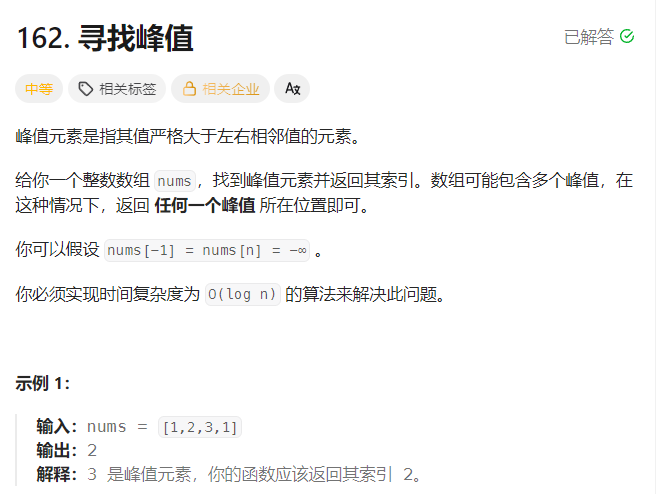
题目解析:
这道题目和第五到题目求山脉数组的峰顶索引是一模一样的,并且连代码都几乎毫无区别,所以这里就不再过多解释
代码示例:
class Solution {
public:int findPeakElement(vector<int>& nums) {int left =0 ,right = nums.size()-1;while(left < right){int mid = left+(right - left)/2; //当我们的找到的mid所对应的值大于mid+1对应的值时,我们可以发现mid可能是返回值,所 //以下一步的缩小区域就只能让right等于midif(nums[mid] > nums[mid +1]) right = mid;//当mid所对应的值小于mid+1对应的值时,此时mid不可能是要求的返回值,所以我们可以让 //left = mid+1;else left = mid +1;}return left;
};7.点名
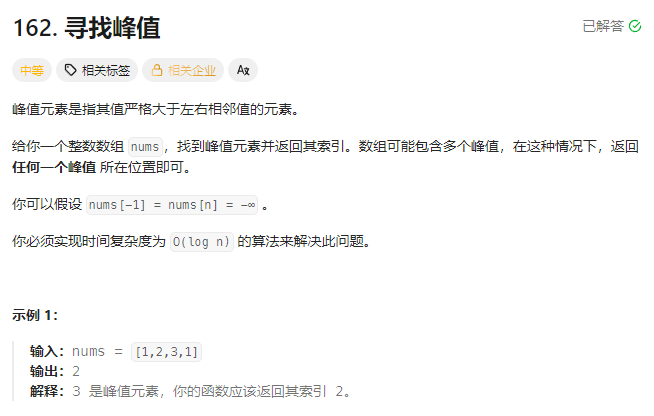
题目解析:
这道题目就是在一个有序数组中找到缺失的那位数,还是很简单的;
算法思路:
这道题目的解法有很多,暴力解法,位运算,哈希表,数学中的高斯求和,我们这里用二分查找来解决这道题目,由于数组是有序的,从0开始,所以每个数都是和它在数组中的下标所对应的,当我们第一次出现不对应的位置时,这个位置的下标就是我们要找的值,所以,这也是符合我们所用二分算法所需要的”二段性“;
代码示例:
class Solution {
public:int takeAttendance(vector<int>& records) {int left = 0,right = records.size()-1;while(left <right){int mid = left+(right - left)/2;//当数组中的值和和我们的下标相等的时候,此时mid一定不会是我们要找的目标值,所以 //left=mid+1;if(records[mid] == mid ) left = left+1;//当不相等的时候,此时的mid可能时我们的返回值,所以缩小区间只能让right = midelse right = mid;}//当数组中都是有序的时候,此时就是少了最后一个人,所以我们返回left+1return left == records.back() ? left +1: left;}