GJOI 11.11 题解

不知道哪里来的题目，感觉质量一般。听说是广大附中交换过来的。

1.洛谷 P1031 NOIP2002 均分纸牌 加强版

题意

思路

先研究要怎么相互给牌，记应该拿到的牌为 $need=\frac{\sum _{i=1}^n{a}_i}{n}$：

• $need\le a_i$：把自己的牌给后面的人；
• $need>a_i$：看 $i+1$ 的牌是否 $\ge need-a_i$，如果不能就继续往后找——直到有一个 $x$，$a_x\ge \sum _{t=i}^{n}need-a_i$，即找到一个人能够补足前面的人所有空缺，然后直接跳到 $x$。

这么看，时间复杂度均摊下来是 $O(n)$。而题目要求移动的字典序最小，因此可以想到答案应该长成：

• 一对 $x\to y$ 至多出现一次；
• 理想情况是 $i\to i+1$，如果 $need>a_i$ 就找到那个 $x$，然后 $x\to x-1$，$x-1\to x-2$，……，$i+1\to i$。

因为要先输出最小操作次数，所以就按照相互给牌的方法去模拟（即洛谷 P1031），记 $b_i=a_i-need$，$t_i=1/-1$ 为 $i$ 与 $i+1$ 的操作标记（决定是 $i\to i+1$ 还是 $i+1\to i$），按照 $b_i$ 的正负分类决定 $t_i$，每次都 $b_{i+1}\leftarrow b_i$。

然后就是像上文那样模拟方案。具体细节见代码。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=3e5+9;
ll n,a[N],b[N];
ll t[N];
ll sum;
int main()
{scanf("%lld",&n);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);sum+=a[i];}ll cnt=0;ll need=sum/n;bool flag=1;for(int i=1;i<=n;i++){b[i]=a[i]-need;if(b[i])flag=0;}if(flag){puts("0");return 0;}for(int i=1;i<=n;i++){if(b[i]>0){b[i+1]+=b[i];b[i]=0;t[i]=1;cnt++;}else if(b[i]<0){b[i+1]-=abs(b[i]);b[i]=0;cnt++;t[i]=-1;}else continue;}//其实求cnt和方案可以放一起，只是懒得存答案了printf("%lld\n",cnt);for(ll i=1;i<=n;i++)//保证i-1都处理好了{if(t[i]==1){printf("%lld %lld %lld\n",i,i+1,a[i]-need);a[i+1]+=a[i]-need;a[i]=need;}if(t[i]==-1){if(need-a[i]<=a[i+1])//i+1 可以承担 i 的补足{printf("%lld %lld %lld\n",i+1,i,need-a[i]);a[i+1]-=need-a[i];a[i]=need;}else //向后找到一个 x=pos，可以承担前面所有{ll pos=i,sum=0;while(pos<=n&&(t[pos]==-1&&sum+need-a[pos]>a[pos+1])){sum+=need-a[pos];pos++;}sum+=need-a[pos];for(ll j=pos;j>=i;j--){printf("%lld %lld %lld\n",j+1,j,sum);a[j+1]-=sum;sum-=need-a[j];a[j]+=sum;}i=pos;//前面都处理完了，直接跳到后面}}}return 0;
}

2.吞噬变异

题意

思路

终于自想到一道建模题了。

考虑模拟一种“松弛操作”，设 $f_i$ 表示得到异兽 $i$ 的最小花费，有初始化 $f_i=a_i$，然后对于可以合成异兽 $x$ 的 $u,v$ 建边，然后不断跑 spfa 或 dijkstra：

如果 $f_u+f_v<f_x$，那么 $f_x$ 被更新，$x$ 和某只异兽 $y$ 能够合成的异兽 $z$ 可能可以更新，于是把 $x$ 扔进（优先）队列即可。

时间复杂度 $O(n?)/O(n\log n)$。下面给出 spfa 的实现。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pll pair<ll,ll>
#define mk make_pair
#define fi first
#define se second
const ll N=1e5+9;
ll n,m,a[N];
struct edge
{ll to,next,pas;
}e[N<<1];
ll idx,head[N];
void addedge(ll u,ll v,ll pas)
{idx++;e[idx].to=v;e[idx].next=head[u];e[idx].pas=pas;head[u]=idx;
}
ll f[N];
void spfa()
{queue<pll>q;for(int i=1;i<=n;i++){f[i]=a[i];q.push(mk(a[i],i));}while(!q.empty()){pll tem=q.front();q.pop();ll u=tem.se;for(int i=head[u];i;i=e[i].next){ll v=e[i].to,pas=e[i].pas;if(f[u]+f[v]<f[pas]){f[pas]=f[u]+f[v];q.push(mk(f[pas],pas));}}}
}
int main()
{scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++)scanf("%lld",&a[i]);for(int i=1;i<=m;i++){ll u,v,pas;scanf("%lld%lld%lld",&u,&v,&pas);addedge(u,v,pas);addedge(v,u,pas);}spfa();for(int i=1;i<=n;i++)printf("%lld ",f[i]);return 0;
}

3.连线问题

题意

思路

还原出每个点的坐标，对 $y=a$ 那列的每个横坐标 $x{a}_i$，贪心地在 $x{b}_i$ 上二分第一个 $\ge$ 它的和第一个 $\le$ 它的，然后跑 MST。

为什么这样建边就是最优的？假使现在就只有 $x{a}_i$，第一个比 $x{a}_i$ 大的 $x{b}_j$ 和 $x{b}_{j+1}$，同样都要连接 $x{b}_j\to x{b}_{j+1}$，显然 $x{a}_i\to x{b}_j$ 的长度要短于 $x{a}_i\to x{b}_{j+1}$（三角函数）。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define dd double
const ll N=6e5+9;
ll n,m,t;
dd a0,b0;
dd aa[N],bb[N];
struct bian
{ll u,v;dd w;
}b[N<<2];
bool cmp(bian x,bian y)
{return x.w<y.w;
}
ll fa[N<<1];
ll fz(ll x)
{while(x!=fa[x])x=fa[x]=fa[fa[x]];return x;
}
dd Dis(ll xa,ll ya,ll xb,ll yb)
{return sqrt((xa-xb)*(xa-xb)+(ya-yb)*(ya-yb));
}
dd kruskal()
{for(int i=1;i<=n+m;i++)fa[i]=i;sort(b+1,b+t+1,cmp);dd ret=0;ll cnt=0;for(int i=1;i<=t;i++){ll fu=fz(b[i].u),fv=fz(b[i].v);if(fu==fv)continue;fa[fu]=fv;ret+=b[i].w;cnt++;if(cnt==n+m-1)break;}return ret;
}
int main()
{scanf("%lld%lld%lf%lf",&n,&m,&a0,&b0);ll tot=0;dd curx=0;for(int i=1;i<=n;i++){dd x;scanf("%lf",&x);curx+=x;aa[i]=curx;if(i>1)b[++t]=(bian){i-1,i,x};}curx=0;for(int i=1;i<=m;i++){dd x;scanf("%lf",&x);curx+=x;bb[i]=curx;if(i>1)b[++t]=(bian){i-1+n,i+n,x};}for(int i=1;i<=n;i++){//第一个大于的 if(aa[i]<bb[m]){ll pos=upper_bound(bb+1,bb+m+1,aa[i])-bb;b[++t]=(bian){i,pos+n,Dis(aa[i],a0,bb[pos],b0)};}//第一个小于等于的 if(aa[i]>=bb[1]){ll pos=upper_bound(bb+1,bb+m+1,aa[i])-bb-1;b[++t]=(bian){i,pos+n,Dis(aa[i],a0,bb[pos],b0)};}}printf("%.2lf",kruskal());return 0;
}

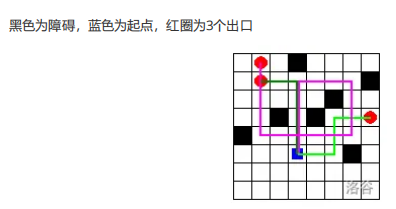
4.走迷宫

题意