【电机控制】基于STM32F103C8T6的二轮平衡车设计——LQR线性二次线控制器（算法篇）

【电机控制】基于STM32F103C8T6的二轮平衡车设计——LQR线性二次线控制器（算法篇）

---

前言

提示：以下是本篇文章正文内容，下面案例可供参考
PID控制器和LQR控制器各有优劣，
LQR控制器更依赖物理模型的建立，也就是白盒实验，需要知道系统内部，再进行调参；
而PID控制器给我的感受是，黑盒实验，即不需要知道物理模型，根据输出响应，直接调参就可以了；
当然，有同学会反驳我，PID控制器也需要物理模型，不可否认，PID也有白盒实验的情况；
但是，大多数的工程，还是经验调参，而不是算了半天，算完再调；
可能这也是为什么大家用脚投PID一票的原因吧；
遇事不决PID大法好…

【电机控制】基于STM32F103C8T6的二轮平衡车设计

一、实验目的

在二轮平衡小车的项目中，落地LQR线性二次型算法；

二、实验步骤一：MATLAB仿真验证

与卡尔曼滤波算法验证不同的是，LQR控制器的设计最终需要反馈增益矩阵K值，在代码里，K值是给定值，不是在代码里在线计算，而是离线进行仿真计算；
因此，需要先离线，在MATLAB中进行仿真；
【电机仿真】LQR控制器——二轮平衡小车控制
再将K值代入到代码里，在线验证；

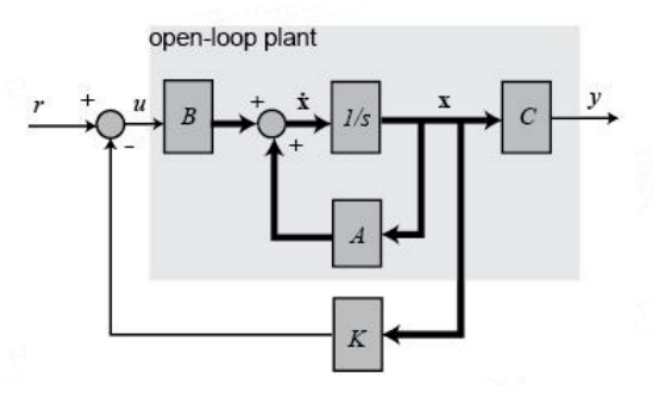
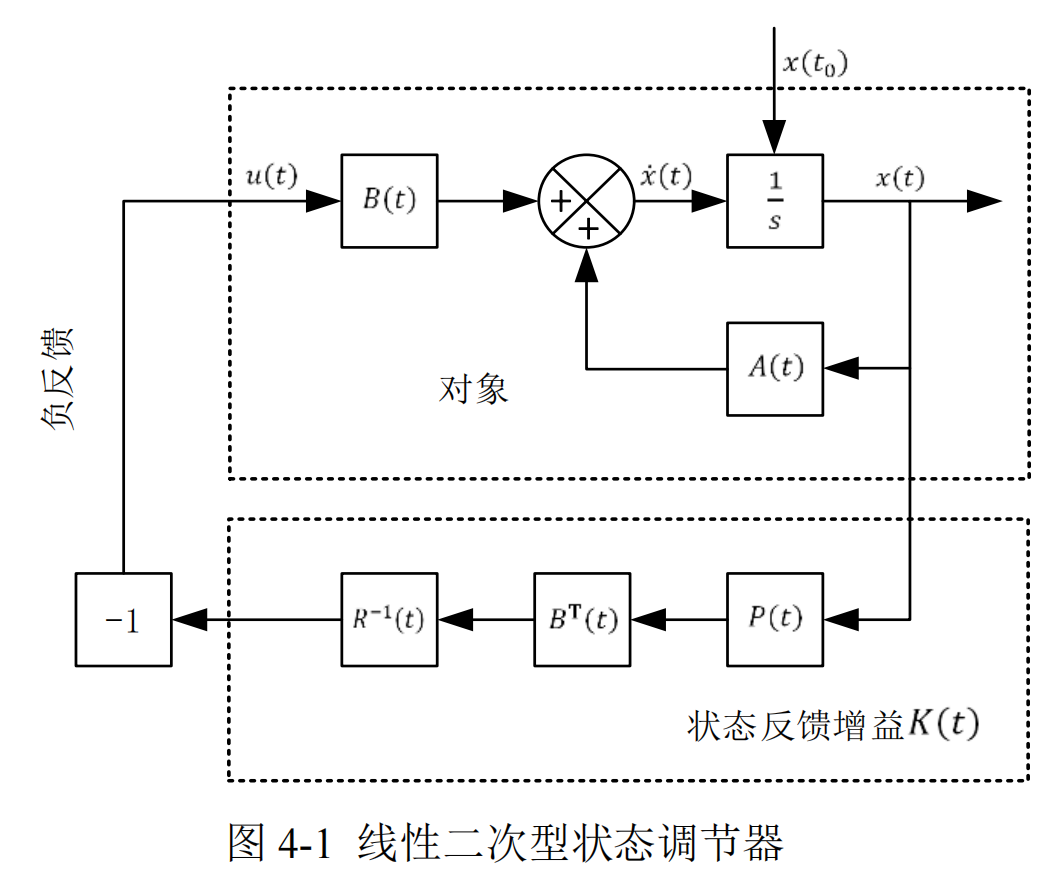
最优控制在现代控制理论中有着及其重要的位置，其研究目标是使受控系
统的性能指标达到最优时，所需要的基本条件，及其控制的综合方法。
线性二次型（LQR）控制，是一种线性状态反馈控制方法，是最优控制理
论中最成熟、最系统的方法。

1.系统状态方程

a.理论

b.代码

因为是离线控制，所以推导K的代码没有在STM32中；
输入参数为举例，并不代表本项目实际使用的输入参数
在MATLAB代码中，建立系统方程的步骤如下

m = 0.035;
r = 0.0672/2;
i = 0.5*m*r^2;
M = 0.757-2*m;
L = 0.5*0.0903;
J_p = (1/12)*M*(0.0903^2+0.0530^2);
d = 0.1612;
J_delta = (1/12)*M*(0.0930^2+0.0530^2);
g = 9.8;
Q_eq = J_p*M+(J_p+M*L^2)*(2*m+2*i/r^2);
A_23 = -(M^2*L^2*g)/Q_eq;
A_43 = M*L*g*(M+2*m+2*i/r^2)/Q_eq;
B_21 = (J_p+M*L^2+M*L*r)/(Q_eq*r);
B_22 = B_21;
B_41 = -(M*L/r+M+2*m+2*i/r^2)/Q_eq;
B_42 = B_41;
B_61 = 1/(r*(m*d+i*d/r^2+2*J_delta/d));
B_62 = -B_61;
A = [0 1 0 0 0 0; 0 0 A_23 0 0 0; 0 0 0 1 0 0; 0 0 A_43 0 0 0; 0 0 0 0 0 1; 0 0 0 0 0 0];
B = (i/r)*[0 0; B_21 B_22; 0 0; B_41 B_42; 0 0; B_61 B_62];

c.分析

状态方程中，状态转移矩阵内A和输入矩阵B的具体推导过程如下：
【电机仿真】LQR控制器——二轮平衡小车控制

2.性能指标

a.理论

性能泛函包含两项，一是系统的积累跟踪误差，二是控制能量。显然它着重权衡和惩罚大的跟踪积累误差和大的控制能量。泛函J取得极小值的含义是：在没有过大控制能量消耗的前提下，使系统输出量 Y(t)尽量接近理想输出量 r(t)，即跟踪误差最小。根据以上条件，最优控制存在且唯一。

b.代码

    Q = [1000 0 0 0 0 0; 0 0 0 0 0 0; 0 0 0 0 0 0; 0 0 0 1000 0 0; 0 0 0 0 1000 0; 0 0 0 0 0 0];R = [1 0; 0 1];

c.分析

Q的设置体现控制优先级：代码中Q(1,1)=1000**（位移误差）、Q(4,4)=1000（俯仰角速度误差）、Q(5,5)=1000（转向角误差）**，说明优先保证这三个状态的精度。R的设置限制控制量：R=eye(2)表示左 / 右轮力的代价相同，避免电机输出过大（如急加速导致的不稳定）。

3.Riccati代数方程——求K

a.理论

若有最优解，则Riccati代数方程=0，可求解P
求解P后可求解K

b.代码

K = lqr(A,B,Q,R);  % 调用MATLAB的lqr函数，输入A、B、Q、R，输出6×2增益矩阵K

在MATLAB代码底层函数中，可以看到

c.分析

对于连续时间系统，基于状态方程中的微分方程，性能函数为求积分，对应的Riccati代数方程为

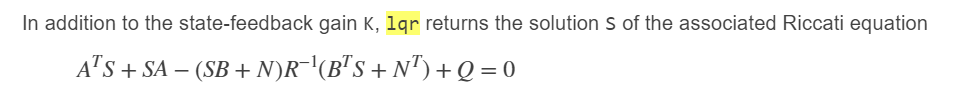
对于离散时间系统，基于状态方程中的差分方程，性能指标是离散求和形式，底层会调用离散 Riccati 方程的求解逻辑

4.反馈增益矩阵K——求u

a.理论

求解K后，可求解u

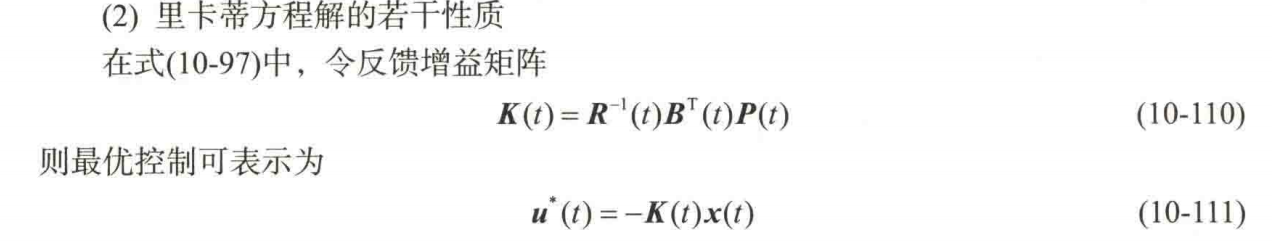
b.代码

最终，终于有STM32的代码，其实只有这两行；

L_accel=-(K1*x_pose+K2*(x_speed-Target_x_speed)+K3*(angle_x-Target_angle_x)+K4*gyro_x+K5*angle_z+K6*(gyro_z-Target_gyro_z));
R_accel=-(K1*x_pose+K2*(x_speed-Target_x_speed)+K3*(angle_x-Target_angle_x)+K4*gyro_x-K5*angle_z-K6*(gyro_z-Target_gyro_z));

c.分析

由于理论模型与实际小车存在误差（如摩擦、传感器噪声），仿真得到的K可能需要微调：

若小车平衡不稳定（左右摇晃）：
增大K3（倾角误差权重）或K4（倾角角速度权重）；

若转向过冲（转角度度过大）：
减小K5或K6；若速度跟踪不准：
增大K2（速度误差权重）。

四、实验结论

验证二轮平衡小车中，联立代码，分析理论，验证LQR线性二次线控制器算法的可行性；

五、参考资料

【电机仿真】LQR控制器——二轮平衡小车控制
【最优控制】5_线性二次型调节器(LQR)详细数学推导

总结

本文仅仅简单介绍了【电机控制】基于STM32F103C8T6的二轮平衡车设计——LQR线性二次线控制器（算法篇），评论区欢迎讨论。