当前位置：首页 > news >正文

基于PVLIB的光伏发电量计算模型：SAPM-Sandia模型的原理与全流程解析

news 2025/11/15 12:42:26

1. 引言

光伏组件的输出功率受到太阳高度角、光谱特性、大气质量、组件温度以及逆变器效率等多重因素共同影响。传统经验模型通常只描述部分环节，难以覆盖从辐照获取、光谱与角度修正、电池温度影响，到组件/逆变器电气特性的完整能量转换链路。

PVLIB-Python 为光伏系统建模提供了端到端的物理建模框架，包括：

太阳位置与大气质量模型
辐照度分解与倾斜面辐照度计算
组件温度模型
功率—电流曲线（IV curve）与直流功率模型
逆变器模型与交流功率计算

其中，SAPM（Sandia Array Performance Model） 是最完整、工程化程度最高的组件性能模型，支持光谱响应、入射角损失、电池温度、电压/电流辐照度修正等多维度效应。与 Sandia 逆变器模型联合后，可构成业界广泛采用的组件—逆变器联合建模方案。

本文的主要工作如下：

系统解析 PVLIB 中 SAPM 模型链条的物理机理与计算流程。
总结 SAPM 的关键参数物理意义、模型假设与工程取值范围。
给出与 pvlib 源码一致的数学公式与伪代码，便于复现与科研使用。

2. 模型总体框架

光伏发电量计算是一个多阶段能量转换过程，涉及天文模型、辐照度几何变换、光谱修正、组件热行为、电池电性能以及逆变器控制策略等环节。整体流程如图 1 所示：
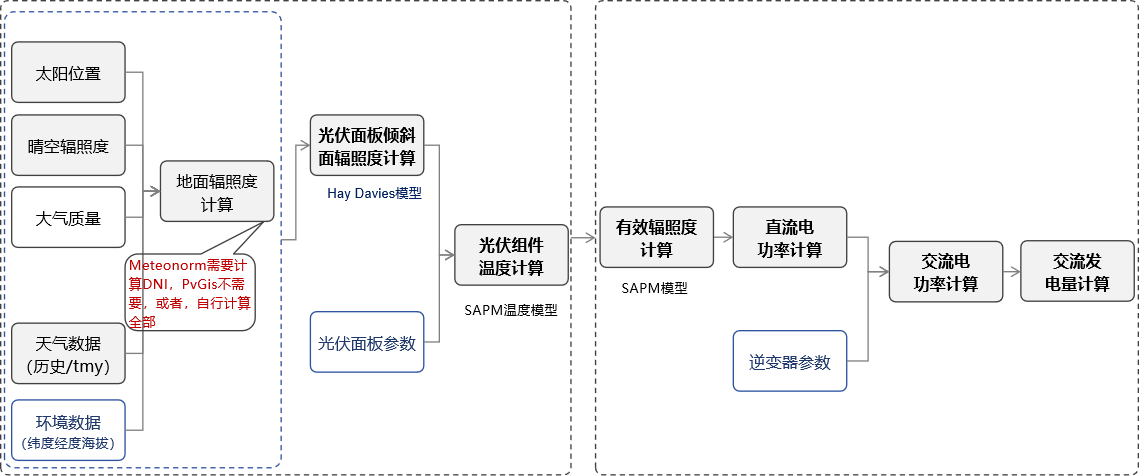
在这里插入图片描述

如下图所示，PVLIB 的四级模型链包括：

太阳位置 → 大气质量 → 晴空辐照度
GHI/DHI/DNI → 倾斜面辐照度（POA）
SAPM 温度模型 → 电池温度
SAPM 有效辐照度 → 直流功率 → Sandia 逆变器 → 交流功率

该流程适用于设计阶段性能评估、运行阶段性能诊断，以及微电网与储能系统中的实时能量管理。下面将逐一深入探讨各环节的公式推导、参数选取。

3. 太阳位置与辐照度计算

3.1. 太阳位置

PVLIB 中 solarposition.get_solarposition 采用 SPA/NOAA 等天文算法，输入经纬度、时间戳，输出太阳高度角、天顶角和方位角。

3.2. 大气质量（AM）

使用atmosphere.get_relative_airmass和atmosphere.get_absolute_airmass计算相对大气质量，默认采用Kasten-Young 1989模型。

$\frac{1}{\cos(\theta_z) + 0.50572 \times (96.07995 - \theta_z)^{-1.6364}}$

其中：

$θz\theta_z$ = 太阳天顶角（度）
当 $θz>90∘\theta_z > 90^\circ$ 时，返回NaN

绝对大气质量通过标准气压修正得到：
$AMa=AM⋅P101325AM_a = AM \cdot \frac{P}{101325}$

3.3. 晴空辐照度

缺乏观测数据时，没有实测辐照度数据（irradiance=None），clearsky.ineichen 模型可计算晴空下的直接辐照度（DNI）、水平总辐照度（GHI）和散射辐照度（DHI），是行业标准的快速晴空模型。

4. 光伏阵列倾斜面辐照度计算

光伏阵列倾斜面总辐照度：是将水平面辐照度转换为倾斜面辐照度（POA），由直接、散射和反射分量三部分组成，公式为：
$POAtotal=POAdirect+POAdiffuse+POAgroundPOA_{\text{total}} = POA_{\text{direct}} + POA_{\text{diffuse}} + POA_{\text{ground}}$

在 pvlib 中由 irradiance.get_total_irradiance 计算，默认使用 Hay–Davies 散射模型。

POA全局辐照度的完整公式：
$POAglobal=DNIcos⁡(AOI)+DHI[(1−F)1+cos⁡β2+FRb]+GHIρ1−cos⁡(β)2POA_{global} = DNI \cos(AOI) +DHI \left[(1-F)\frac{1+\cos\beta}{2} + F R_b\right]+ GHI \rho \frac{1 - \cos(\beta)}{2}$

其中：

$\frac{DNI} {E_0}$ ，晴朗指数，采用Spencer 1971方法（默认）：
- $E0=1366.1×[1.000110+0.034221cos⁡(b)+0.001280sin⁡(b)+0.000719cos⁡(2b)+0.000077sin⁡(2b)]E_0 = 1366.1 \times \left[1.000110 + 0.034221\cos(b) + 0.001280\sin(b) + 0.000719\cos(2b) + 0.000077\sin(2b)\right]$
- 其中：
  - $\frac{2\pi(doy - 1)}{365}$ （日角，弧度）
  - $d oy$ = 一年中的第几天（1-365）
$Rb=cos(AOI)cos(θz)R_b = \frac{cos(AOI)} {cos(θ_z)}$ ，倾斜面与水平面直射投影比
$A O I$ 为入射角
$arccos[\cos(\beta)\cos(\theta_{z}) + \sin(\beta) \sin(\theta_{z} )\cos(\phi_{s} - \phi)]$
- $θz\theta_{z}$ ：太阳天顶角，solar_zenith。
- $β\beta$ ：光伏阵列倾角（度），surface_tilt。
- $ϕs\phi_{s}$ ：太阳方位角，solar_azimuth。
- $ϕ\phi$ ：阵列方位角（北极为0°，南极为180°，东为90°）。

备注：详见光伏阵列平面辐照度（POA）计算模型分析与公式推导。

关键参数说明

参数	单位	默认值	说明
DNI	W/m²	-	法向直射辐照度，需通过太阳位置算法计算
DHI	W/m²	-	水平散射辐照度
GHI	W/m²	-	水平全局辐照度
$β\beta$	度	用户输入	光伏阵列与水平面的夹角
$ϕ\phi$	度	用户输入	阵列方位角（北为0°，东为90°，南为180°）
$ρ\rho$	-	0.25	地面反射率（草地0.2，雪地0.8，水面0.06）

注：pvlib使用通过pvlib.irradiance.get_total_irradiance计算。

5. 组件温度计算

温度模型：默认使用SAPM（Sandia Array Performance Model）温度模型，SAPM温度模型是一种基于经验的物理模型，用于预测光伏组件在不同环境温度和辐照度条件下的直流输出功率，其核心是通过温度修正系数量化温度对组件性能的影响，并结合辐照度、组件参数等输入变量进行功率计算，在PVLIB中通过temperature.sapm_cell计算电池温度。

5.1 模型公式

SAPM 温度模型为经验–物理混合模型，用于计算组件电池温度：

$Tcell=Tair+EPOAea+bWS+(EPOA1000)ΔTT_{cell} = T_{air} + E_{POA} e^{a + b WS} + \left(\frac{E_{POA}}{1000}\right) \Delta T$

其中：

$T_{air}$ 为环境温度 (°C)
$E_{POA}$ 为斜面总辐照度 (W/m²)
$W S$ 为风速 (m/s)
$\Delta T$ 为SAPM温度模型参数，取决于安装方式和模块类型
$EPOA×ea+b×WSE_{POA} \times e^{a + b \times WS}$ ：辐照度引起的温升，受风速影响
$EPOA1000×ΔT\frac{E_{POA}}{1000} \times \Delta T$ ：辐照度相关的温度修正项

5.2. SAPM 温度模型的 4 种参数组合

模型名称	安装方式	封装材料	a (℃/(W/m²))	b (℃/(m/s))	deltaT (℃)
`open_rack_glass_glass`	开放式支架	双层玻璃	-3.47	-0.0594	3
`close_mount_glass_glass`	密闭安装	双层玻璃	-2.98	-0.0471	1
`open_rack_glass_polymer`	开放式支架	玻璃+聚合物背板	-3.56	-0.0750	3
`insulated_back_glass_polymer`	背板保温型	玻璃+聚合物背板	-2.81	-0.0455	0

表格说明

安装方式：
- open_rack：开放式支架（如地面电站），通风良好。
- close_mount：密闭安装（如屋顶），通风受限。
- insulated_back：背板带保温层（如寒冷地区），减少热损失。
封装材料：
- glass_glass：双层玻璃封装，透光率高但散热一般。
- glass_polymer：玻璃前板+聚合物背板（如PVDF），背板散热更优。
参数物理意义：
- a：辐照度每增加1 W/m²，组件温度变化（℃）。绝对值越大，温度对辐照度越敏感。
- b：风速每增加1 m/s，组件温度变化（℃）。绝对值越大，散热对风速响应越强。
- deltaT：基准温度偏移量，补偿模型误差或环境因素（如地面反射热）。

6. SAPM 有效辐照度计算方法

在 pvsystem.py 中，sapm_effective_irradiance 函数实现了SAPM模型的有效辐照度计算，输入参数：

poa_direct, 入射到模块的直射辐照度。[W/m²]
poa_diffuse，入射到模块的散射辐照度。[W/m²]
airmass_absolute，绝对大气质量（无量纲）。
aoi，入射角（太阳光线与模块法线的夹角）。[度]

计算公式解析
$Ee=f1(AMa)(Ebf2(AOI)+fdEd)E_e = f_1(AM_a) \left( E_b f_2(AOI) + f_d E_d \right)$

变量定义：

$E_e$ ：有效辐照度（Effective Irradiance），即光伏组件实际吸收并转化为电能的辐照度（单位：W/m²）。
$AM_a$ ：大气质量（Air Mass），描述太阳光穿过大气层的路径长度（与太阳高度角相关）。
$E_b$ ：平面上的直射辐照度（Beam Irradiance）。
$A O I$ ：入射角（Angle of Incidence），即太阳光线与光伏平面法线的夹角。
$E_d$ ：平面上的散射辐照度（Diffuse Irradiance）。
$f_1(AM_a)$ ：与大气质量相关的修正函数（通常为多项式）。
$f_2(AOI)$ ：与入射角相关的直射辐照度修正函数（通常为多项式）。
$f_d$ ：散射辐照度的吸收比例（与表面反射率相关）。

模型物理意义

大气质量修正（ $f_1(AM_a)$ ）：
- 大气质量影响太阳光谱分布和强度。例如，当太阳高度角较低时（如清晨/傍晚），大气质量增大，光线穿过更厚的大气层，导致短波长光被散射或吸收更多。
- $f_1(AM_a)$ 通常通过实验数据拟合为四次多项式，用于修正不同大气质量下的辐照度。
直射辐照度修正（ $E_b f_2(AOI)$ ）：
- 直射辐照度 $E_b$ 随入射角 $A O I$ 变化显著。当 $A O I$ 增大（光线更倾斜），反射损失增加，实际被吸收的辐照度减少。
- $f_2(AOI)$ 通常为五次多项式，描述入射角对直射辐照度吸收效率的影响。
散射辐照度修正 $f_d E_d$ ）：
- 散射辐照度 $E_d$ 来自大气散射，分布较均匀。
- $f_d$ 表示光伏平面未反射的散射辐照度比例，与表面材料（如玻璃涂层）的反射率相关。

参数获取：

$E_b$ 和 $E_d$ 可通过气象站或卫星数据获取。
$AM_a$ 和 $A O I$ 需通过太阳位置算法（如SPA算法）计算。
局限性：多项式函数需通过实验数据拟合，通用性受限。

示例计算
假设：

$AM_a = 1.5$ ， $Eb=800W/m²E_b = 800\ \text{W/m²}$ ， $A O I = 30°$ ， $Ed=200W/m²E_d = 200\ \text{W/m²}$ ，
$f_1(1.5) = 0.95$ ， $f_2(30°) = 0.98$ ， $f_d = 0.9$ 。

则有效辐照度为：
$Ee=0.95×(800×0.98+0.9×200)=0.95×(784+180)=916.4W/m².E_e = 0.95 \times \left( 800 \times 0.98 + 0.9 \times 200 \right) = 0.95 \times (784 + 180) = 916.4\ \text{W/m²}.$

6.1. 大气质量修正（ $f_1(AM_a)$ ）

pvlib.spectrum.spectral_factor_sapm 使用Sandia阵列性能模型（Sandia Array Performance Model, SAPM）方法计算光谱修正因子 $f_1$ 。输入参数为：

airmass_absolute，绝对大气质量（无量纲）
注：若输入为np.nan，则输出为0。
module，定义SAPM参数的字典、Series或DataFrame，必须包含键'A0'至'A4'。更多详细信息请参见pvlib.pvsystem.sapm()的注释部分。

SAPM光谱因子函数是更广泛的Sandia阵列性能模型的一部分，该模型使用基于经验的光伏组件特定系数定义IV曲线上的五个点。SAPM的组件系数可从SAPM数据库中获取。并通过pvlib.pvsystem.retrieve_sam()在组件参数中使用。有关SAPM的更多详细信息，请参见[2]；关于确定经验模型系数（包括SAPM光谱修正系数）的完整流程描述，请参见[3]。SAPM光谱修正函数将 $f_1$ 参数化为绝对大气质量的四次多项式函数：

$f1=A0+A1⋅AMa+A2⋅AMa2+A3⋅AMa3+A4⋅AMa4f_1 = A_0 + A_1 \cdot AM_a + A_2 \cdot AM_a^2 + A_3 \cdot AM_a^3 + A_4 \cdot AM_a^4$

其中：

$f_1$ 为光谱修正因子，
$A0∼A4A_0 \sim A_4$ 为组件特定系数，
$AM_a$ 为绝对大气质量（通过对相对大气质量进行气压校正计算得出）。

有关此光谱修正函数的开发细节，请参见[4]。

6.2. 入射角修正系数 $f_2(AOI)$

数学公式：
$f2(AOI)=B0+B1×AOI+B2×AOI2+B3×AOI3+B4×AOI4+B5×AOI5f_2(AOI) = B_0 + B_1 \times AOI + B_2 \times AOI^2 + B_3 \times AOI^3 + B_4 \times AOI^4 + B_5 \times AOI^5$

其中：

$A O I$ 为入射角（单位：度）
$B_0$ 到 $B_5$ 是模块的入射角修正系数，取自SAPM数据库。

6.3. 散射辐照度系数 $f_d$

直接从模块参数中获取：

FD = module['FD']  # 通常在 0.95-1.0 之间

SandiaMod数据模型

retrieve_sam("sandiamod")对应data/sam-library-sandia-modules-2015-6-30.csv

6.4. SAPM模型具体展开

$Ee=(∑i=04Ai⋅AMai)×[Eb×(∑j=05Bj⋅AOIj)+fd×Ed]E_{e} = \left( \sum_{i=0}^{4} A_i \cdot AM_a^i \right) \times \left[ E_b \times \left( \sum_{j=0}^{5} B_j \cdot AOI^j \right) + f_d \times E_d \right]$

其中：

$A O I$ = 入射角 (AOI, degrees)
$AM_a$ = 绝对大气质量 (unitless)
$A_i$ = 光谱修正多项式系数
$B_j$ = 入射角修正多项式系数
$f_d$ = 散射辐照度系数

合成有效辐照度，将修正后的直接和散射分量相加，得到真正被光伏电池吸收并转换为电能的有效辐照度。这种"先分解、后修正、再合成"的方法比整体修正更符合物理实际，能够更准确地描述不同辐照度分量对光伏发电的影响。

6.5. 关键代码与公式对应关系

数学符号	代码变量	说明
$E_e$	`Ee`, `effective_irradiance`	有效辐照度
$f_1$	`F1`, `spectral_modifier`	光谱修正系数
$f_2$	`F2`, `aoi_modifier`	入射角修正系数
$f_d$	`FD`, `module['FD']`	散射辐照度系数
$E_b$	`poa_direct`	斜面直接辐照度
$E_d$	`poa_diffuse`	斜面散射辐照度

基于您提供的代码和pvlib源码，我来提取SAPM模型中的直流、交流功率计算公式及相关说明。

7. SAPM 直流模型与 Sandia 逆变器模型

直流功率：

从pvlib源码的pvsystem.sapm函数中提取的直流功率计算公式：

$P_{dc} = I_{mp} V_{mp}$

其中：

$I_{mp}$ = 最大功率点电流
$V_{mp}$ = 最大功率点电压

最大功率点直流电流：

$Imp=Imp0C0Ee[1+αImp(Tcell−Tref)]I_{mp} = I_{mp0} C_0 E_e \left[1 + \alpha_{I_{mp}} (T_{cell} - T_{ref})\right]$

参数说明：

$I_{mp0}$ ：参考条件下的最大功率点电流（来自Impo参数）
$C_0$ ：电流辐照度修正系数
$E_e$ ：有效辐照度（W/m²）
$αImp\alpha_{I_{mp}}$ ：电流温度系数（来自a_imp参数）
$T_{cell}$ ：电池温度（°C）
$T_{ref}$ ：参考温度（25°C）

最大功率点直流电压

$Vmp=Vmp0+C1Nsδ(Tc)+C2Nsδ(Tcell)2+βVmp(Tcell−Tref)V_{mp} = V_{mp0} + C_1 N_s \delta(T_c) + C_2 N_s \delta(T_{cell})^2 + \beta_{V_{mp}} (T_{cell} - T_{ref})$

其中：

$δ(Tcell)=ln⁡(Ee/E0)\delta(T_{cell}) = \ln(E_e / E_0)$
$E_0 = 1000$ W/m²（参考辐照度）

参数说明：

$V_{mp0}$ ：参考条件下的最大功率点电压（来自Vmpo参数）
$C_1, C_2$ ：电压辐照度修正系数
$N_s$ ：串联电池片数量
$βVmp\beta_{V_{mp}}$ ：电压温度系数（来自b_vmp参数）

合并直流功率公式
$Pdc=[Imp0C0Ee(1+αImp(Tc−25))][Vmp0+C1Nsln⁡(Ee1000)+C2Ns(ln⁡(Ee1000))2+βVmp(Tc−Tref)]P_{dc} = \left[I_{mp0} C_0 E_e \left(1 + \alpha_{I_{mp}} (T_c - 25)\right)\right] \left[V_{mp0} + C_1 N_s \ln\left(\frac{E_e}{1000}\right) + C_2 N_s \left(\ln\left(\frac{E_e}{1000}\right)\right)^2 + \beta_{V_{mp}} (T_c - T_{ref})\right]$

关键SAPM参数，从module_parameters中提取的关键参数：

参数	符号	说明	典型值
`Impo`	$I_{mp0}$	参考条件下MPP电流	4.5469 A
`Vmpo`	$V_{mp0}$	参考条件下MPP电压	36.3160 V
`a_imp`	$αImp\alpha_{I_{mp}}$	电流温度系数	0.000534
`b_vmp`	$βVmp\beta_{V_{mp}}$	电压温度系数	-0.13600
`Cells_in_Series`	$N_s$	串联电池片数	60
`C0`	$C_0$	电流辐照度系数	1.0000
`C1`	$C_1$	电压辐照度系数1	-0.002438
`C2`	$C_2$	电压辐照度系数2	0.000310

SAPM直流模型特点

经验基础：基于大量实测数据拟合的经验模型
温度修正：分别考虑温度对电流和电压的影响
辐照度修正：使用对数函数描述辐照度对电压的非线性影响
物理意义明确：每个参数都有明确的物理含义

逆变器交流功率：

从inverter.sandia函数中提取，核心Sandia逆变器交流功率公式：

$Pac=PdcPdc0[Pac0+C1(Pdc−Pdc0)+C2(Pdc−Pdc0)2]P_{ac} = \frac{P_{dc}}{P_{dc0}} \left[P_{ac0} + C_1 (P_{dc} - P_{dc0}) + C_2 (P_{dc} - P_{dc0})^2\right]$

考虑直流电压对效率的影响，电压修正因子：

$Pac=Pac[1+C3(Vdc−Vdc0)+C4(Vdc−Vdc0)2]P_{ac} = P_{ac} \left[1 + C_3 (V_{dc} - V_{dc0}) + C_4 (V_{dc} - V_{dc0})^2\right]$

从inverter_parameters中提取的关键参数：

参数	符号	说明	典型值
`Paco`	$P_{ac0}$	额定交流功率	250 W
`Pdco`	$P_{dc0}$	额定直流功率	259.5 W
`Vdco`	$V_{dc0}$	额定直流电压	40.5 V
`C0`	$C_0$	基本效率参数	-4.11e-05
`C1`	$C_1$	效率曲线系数1	-9.89e-04
`C2`	$C_2$	效率曲线系数2	-9.38e-04
`C3`	$C_3$	电压修正系数1	0.002129
`C4`	$C_4$	电压修正系数2	-0.01493

Sandia逆变器模型特点

多项式拟合：使用二次多项式描述效率曲线
电压修正：考虑直流电压波动对效率的影响
功率限制：确保输出功率不超过额定值
实际数据验证：基于大量逆变器测试数据

完整的SAPM计算流程：

import pvlib
from pvlib import location
from pvlib.modelchain import ModelChain
import pandas as pd
from pvlib.temperature import TEMPERATURE_MODEL_PARAMETERS
from pvlib.pvsystem import PVSystem# 获取组件和逆变器参数
mods = pvlib.pvsystem.retrieve_sam('sandiamod')
invs = pvlib.pvsystem.retrieve_sam('cecinverter')
module_parameters = mods['Canadian_Solar_CS5P_220M___2009_']
inverter_parameters = invs['ABB__MICRO_0_25_I_OUTD_US_240__240V_']
tparams = TEMPERATURE_MODEL_PARAMETERS['sapm']['open_rack_glass_glass']# 虚拟天气数据
weather = pd.DataFrame([[1050, 1000, 100, 30, 5]],columns=['ghi', 'dni', 'dhi', 'temp_air', 'wind_speed'],index=[pd.Timestamp('20250401 1200', tz='Asia/Shanghai')])# 创建光伏系统
system = PVSystem(surface_tilt=30, surface_azimuth=180,module_parameters=module_parameters,inverter_parameters=inverter_parameters,temperature_model_parameters=tparams)# 站点定义
site = location.Location(latitude=31.2, longitude=121.5, tz='Asia/Shanghai')# 创建SAPM模型链
mc = ModelChain(system, site,aoi_model='sapm',spectral_model='sapm',temperature_model='sapm',dc_model='sapm',ac_model='sandia')# 运行模型
mc.run_model(weather)# 输出结果
print("入射角:", mc.results.aoi)
print("电池温度:", mc.results.cell_temperature)
print("直流功率:", mc.results.dc)
print("交流功率:", mc.results.ac)

8. SAPM 模型的工程应用与局限性

工程优势：

基于大量实测数据拟合，精度高于线性经验模型
入射角、光谱效应等物理机制描述完备
逆变器模型能捕捉电压偏离对效率的影响

局限性：

需完整的组件/逆变器 SAPM 参数，国内组件并不总能提供
高纬度地区（如冬季太阳角度大）模型误差可能增大
光谱修正与灰尘污染、积雪等因素的耦合未建模

8. 总结

本文对 PVLIB 中 SAPM 模型链的物理机理进行了系统梳理，包括太阳辐照度建模、组件倾斜面辐照度计算、SAPM 温度模型、有效辐照度模型、Sapm 直流功率以及 Sandia 逆变器交流功率模型。通过对模型源码中参数及公式的拆解，给出了一个可复现、可用于工程仿真与学术研究的完整计算链路。

SAPM 模型的一大优势是将各种物理效应模块化，包括光谱、入射角、温度、电流/电压辐照度修正，使得模型具备较高的可解释性和工程适应性。结合 PVLIB 提供的组件与逆变器数据库，可方便构建从气象数据到交流输出的全面仿真系统，为光伏系统设计、发电预测与性能分析提供了可靠基础。

参考文献：

[1] D. King et al, “Sandia Photovoltaic Array Performance Model”, SAND2004-3535, Sandia National Laboratories, Albuquerque, NM

[2] King, D., Kratochvil, J., and Boyson W. (2004), “Sandia Photovoltaic Array Performance Model”, (No. SAND2004-3535), Sandia National Laboratories, Albuquerque, NM (United States). DOI: 10.2172/919131

[3] King, B., Hansen, C., Riley, D., Robinson, C., and Pratt, L. (2016). Procedure to determine coefficients for the Sandia Array Performance Model (SAPM) (No. SAND2016-5284). Sandia National Laboratories, Albuquerque, NM (United States). DOI: 10.2172/1256510

[4] King, D., Kratochvil, J., and Boyson, W. “Measuring solar spectral and angle-of-incidence effects on photovoltaic modules and solar irradiance sensors.” Conference Record of the 26th IEEE Potovoltaic Specialists Conference (PVSC). IEEE, 1997. DOI: 10.1109/PVSC.1997.654283

[5] B.H. King et al, “Recent Advancements in Outdoor MeasurementTechniques for Angle of Incidence Effects,” 42nd IEEE PVSC (2015).DOI: 10.1109/PVSC.2015.7355849

[6] Holmgren, W. F., Hansen, C. W., & Mikofski, M. A. (2018). pvlib python: a python package for modeling solar energy systems. Journal of Open Source Software, 3(29), 884.

[7] Kasten, F., & Young, A. T. (1989). Revised optical air mass tables and approximation formula. Applied Optics, 28(22), 4735–4738.

[8] Spencer, J. W. (1971). Fourier series representation of the position of the sun. Search, 2(5), 172.

[9] Ineichen, P. (2008). A broadband simplified version of the Solis clear sky model. Solar Energy, 82(8), 758–762.

[10] PVLIB 官方文档：https://github.com/pvlib/pvlib-python

查看全文

http://www.dtcms.com/a/611114.html