磁共振成像原理（理论）31：基本梯度回波成像 (Basic Gradient-Echo Imaging)

本专题主要参考《Principles of Magnetic Resonance Imaging A Signal Processing Perspective 》-Sec 7.5

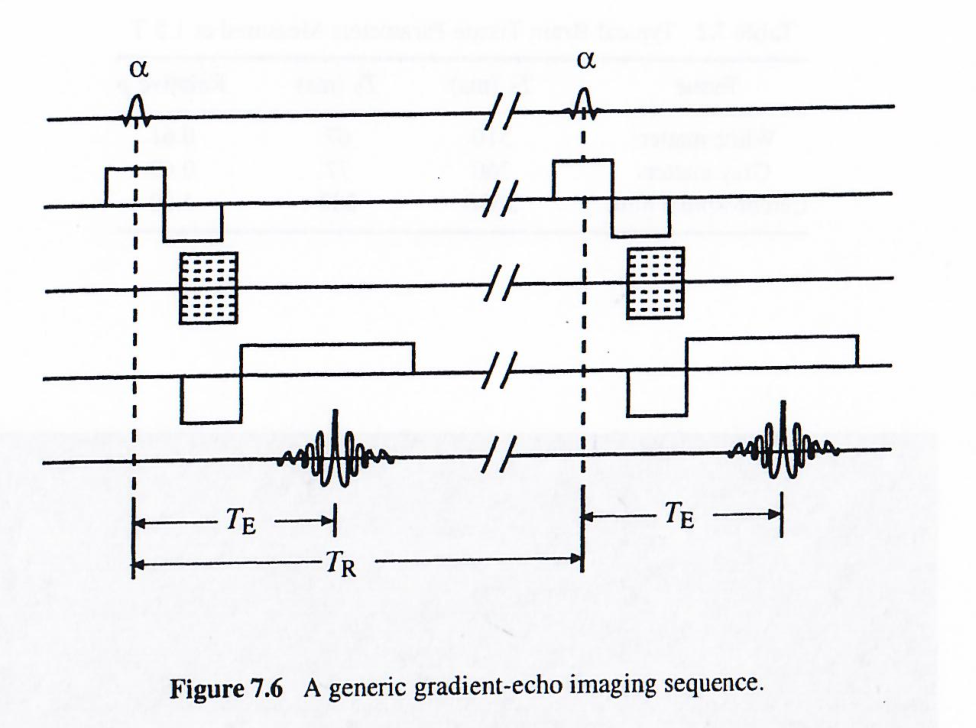
梯度回波成像的基本思想是用梯度重聚脉冲取代自旋回波序列中的180°重聚射频脉冲，如下图所示。这种替代使得使用小角度激发进行快速成像变得高效，这一主题将在后续详细讨论。

与自旋回波成像序列相比，梯度回波成像序列显示出更广泛的变化形式，因此其图像对比机制也显著更加丰富。具体而言，通过适当选择重复时间$T_R$、回波时间$T_E$和翻转角，梯度回波成像序列可以生成具有$T_1$加权、$T_1/T_2$加权、$T_2$加权、$T_2^{\ast }$加权以及自旋密度加权的对比度图像。本节将通过一个具体示例来阐述这一概念。关于其他梯度回波快速成像方法及其对比行为的更深入讨论可以在后面继续讨论。

梯度回波序列的数学模型

考虑上图所示的梯度回波序列（脉冲是$x^{\prime }$方向）。我们假设$T_R\gg T_2$，这意味着来自前一个激励脉冲的横向磁化已完全失相：
$$M_{x^{\prime }{y}^{\prime }}^{(n)}(0_{-})=0\text{\hspace{1em}(7.29)}$$

根据弛豫方程（式3.122）
$$\{\begin{array}{l}{M}_{x^{\prime }{y}^{\prime }}(t)=M_{x^{\prime }{y}^{\prime }}(0_{+})e^{-t/T_2}\\ M_{z^{\prime }}(t)=M_z^0(1-e^{-t/T_1})+M_{z^{\prime }}(0_{+})e^{-t/T_1}\end{array}\text{\hspace{1em}(3.122)}$$

我们得到纵向磁化强度的递推关系：
$$M_{z^{\prime }}^{(n)}(0_{-})=M_z^0(1-e^{-T_R/T_1})+M_{z^{\prime }}^{(n-1)}(0_{+})e^{-T_R/T_1}\text{\hspace{1em}(7.30)}$$

其中$M_{z^{\prime }}^{(n)}(0_{-})$和$M_{z^{\prime }}^{(n-1)}(0_{+})$分别表示第n个脉冲前和第(n-1)个脉冲后的纵向磁化强度，两者的时间间隔就是$T_R$，所以将$t\to T_R$导入3.122即可得到式7.30。

利用$x^{\prime }$方向射频脉冲对纵向磁化强度的影响关系，见式3.91：
$$R_{x^{\prime }}(\alpha )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \alpha & \sin \alpha \\ 0& -\sin \alpha & \cos \alpha \end{array}\right]\text{\hspace{1em}(3.91)}$$

因此得到了$\alpha$脉冲后的纵向磁化强度（注意脉冲前的横向磁化强度是0，因为$T_R\gg T_2$）：
$$M_{z^{\prime }}^{(n)}(0_{+})=M_{z^{\prime }}^{(n)}(0_{-})\cos \alpha \text{\hspace{1em}(7.31 A)}$$
$$M_{x^{\prime }{y}^{\prime }}^{(n)}(0_{+})=M_{z^{\prime }}^{(n)}(0_{-})\sin \alpha \text{\hspace{1em}(7.31 B)}$$
式(7.30)可以重写为：
$$M_{z^{\prime }}^{(n)}(0_{-})=M_z^0(1-e^{-T_R/T_1})+M_{z^{\prime }}^{(n-1)}(0_{-})\cos \alpha \cdot e^{-T_R/T_1}\text{\hspace{1em}(7.32)}$$

稳态条件的建立与求解

当第n-1个脉冲激发前的纵向磁化强度$M_{z^{\prime }}^{(n-1)}(0_{-})$，等于第n个射频脉冲激发前的纵向磁化强度$M_{z^{\prime }}^{(n)}(0_{-})$时，此时系统达到动态稳态。假设这个值是$M_{z^{\prime }}^{ss}(0_{-})$，由此可得：
$$M_{z^{\prime }}^{(n)}(0_{-})=M_{z^{\prime }}^{(n-1)}(0_{-})=M_{z^{\prime }}^{ss}(0_{-})\text{\hspace{1em}(7.33)}$$

将稳态条件代入式(7.32)，得到：
$$M_{z^{\prime }}^{ss}(0_{-})=M_z^0(1-e^{-T_R/T_1})+M_{z^{\prime }}^{ss}(0_{-})\cos \alpha \cdot e^{-T_R/T_1}\text{\hspace{1em}()}$$

整理后求解稳态纵向磁化强度：
$$M_{z^{\prime }}^{ss}(0_{-})(1-\cos \alpha \cdot e^{-T_R/T_1})=M_z^0(1-e^{-T_R/T_1})\text{\hspace{1em}()}$$

即
$$M_{z^{\prime }}^{ss}(0_{-})=\frac{M_z^0(1-e^{-T_R/T_1})}{1-\cos \alpha \cdot e^{-T_R/T_1}}\text{\hspace{1em}(7.34)}$$

横向磁化强度与回波信号

将稳态纵向磁化强度$M_{z^{\prime }}^{ss}(0_{-})$代入式7.31B和3.122，可以得到脉冲后的稳态横向磁化强度，注意此时$T_2\to T_2^{\ast }$，因为射频脉冲激发后，频率编码梯度就一直开着了，它会大大加速横向弛豫过程。
$$M_{x^{\prime }{y}^{\prime }}^{ss}(t)=M_{z^{\prime }}^{ss}(0_{-})\sin \alpha \cdot e^{-t/T_2^{\ast }}\text{\hspace{1em}(7.35)}$$

将式(7.34)代入，得到完整的横向磁化强度表达式：
$$M_{x^{\prime }{y}^{\prime }}^{ss}(t)=\frac{M_z^0(1-e^{-T_R/T_1})}{1-\cos \alpha \cdot e^{-T_R/T_1}}\sin \alpha \cdot e^{-t/T_2^{\ast }}\text{\hspace{1em}()}$$

回波幅度在$t=T_E$时刻为：
$$A_E=\frac{M_z^0(1-e^{-T_R/T_1})}{1-\cos \alpha \cdot e^{-T_R/T_1}}\sin \alpha \cdot e^{-T_E/T_2^{\ast }}\text{\hspace{1em}(7.36)}$$

对比度特性分析

式(7.36)清楚地表明，该梯度回波序列的图像强度同时携带$T_1$和$T_2^{\ast }$加权。$T_2^{\ast }$加权因子是梯度回波序列的特征，可通过调整回波时间$T_E$来控制，这与自旋回波成像序列中调整$T_2$对比度的方式相似。

然而，与自旋回波序列不同，梯度回波序列中的$T_1$对比度主要取决于翻转角$\alpha$而不是重复时间$T_R$。具体来说，当$\alpha$较小时，$\cos \alpha \approx 1$，$T_1$加权因子被消除。随着翻转角的增大，$T_1$加权因子变得更加显著，并且可以通过选择不同的重复时间进一步调节。

讨论

磁共振成像中的主要对比度类型

磁共振成像中有三种主要类型的对比度：自旋密度对比度、$T_1$对比度和$T_2$对比度。自旋密度对比度与组织自旋密度差异呈线性比例关系，而$T_1$和$T_2$对比度分别与组织$T_1$和$T_2$值呈指数关系。

正常软组织通常自旋密度变化较小，但具有差异较大的$T_1$值。因此，$T_1$加权成像是获得良好解剖定义图像的有效方法。许多疾病状态以组织$T_2$值的改变为特征，$T_2$加权成像是一种敏感的疾病检测方法。

对比度调控在实践中的考虑

对于给定的成像序列，所有三种对比度类型都可以对组织对比度做出贡献，但通常只强调其中一种。例如，在自旋回波成像中，可以通过大的$T_R$和小的$T_E$来消除$T_1$和$T_2$因子，得到的图像将是自旋密度加权的。

在实践中，可能的最小$T_E$值通常受系统硬件性能的限制，而最大$T_R$值则受成像时间和实际考虑因素的约束。

图像质量的其他影响因素

虽然大的对比度是良好组织可见性的重要因素，但还有许多其他影响因素，如图像像素大小和噪声。

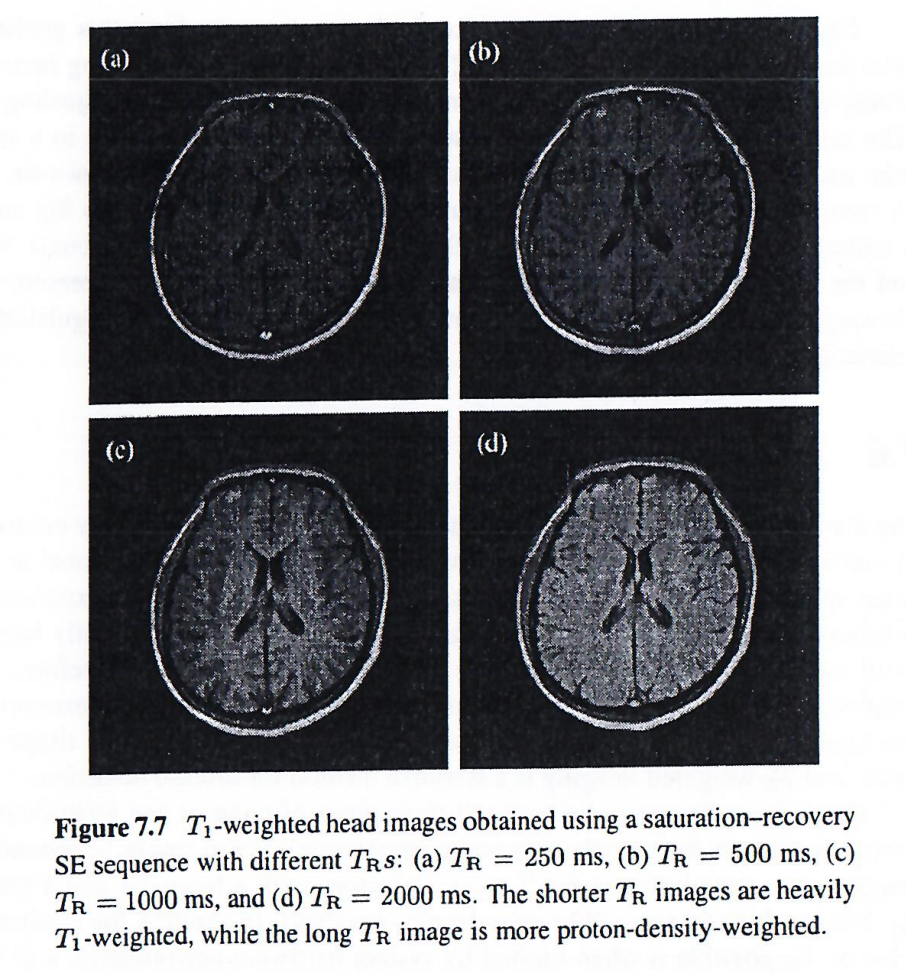
为了说明作为数据采集参数函数的组织对比度概念，下面两图使用具有不同$T_1$和$T_2$加权的饱和恢复自旋回波序列采集的。

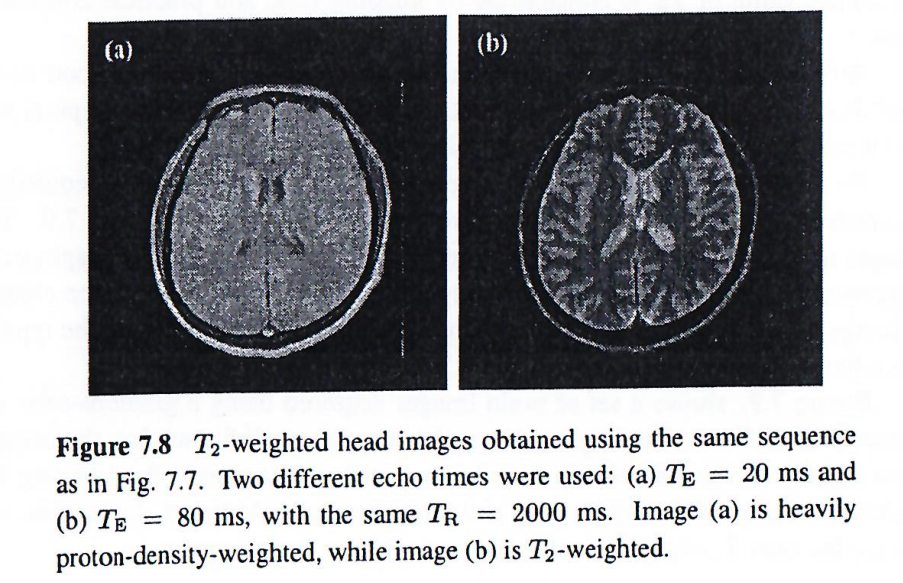
而下图显示了一组使用具有不同翻转角的梯度回波序列采集的脑部图像。可以看出，在小翻转角时，图像主要显示质子密度分布，脑脊液具有最高强度，其次是灰质和白质。在较大翻转角时，图像变为$T_1$加权。