LeetCode hot100:4.寻找两个正序数组的中位数 题解分析
题目分析

题目可以简单粗暴地理解为把两个数组连合在一起,然后再把两个数组排一下序 取中位数。如果没有时间复杂度要求的话这题O(m + n)的暴力做法很简单,但题目要求时间复杂度为O(log (m+n)),这就有很大的难度了。
先说一下基础思路,能否把两个数组再次在逻辑上进行拆分,使得第一个数组的最大值小于第二个数组的最小值,这样就可以根据两个数组长度之和 m + n 进行条件判断是奇数还是偶数再计算中位数。思路在这里,如何将两个数组进行上述的划分呢?
思路讲解
说明:逻辑数组array1、array2,实际数组a、b。
我们要做到array1中的最大值小于array2中的最小值,最开始假设b数组中所有的元素都在array2,a数组中的元素都在array1。初始结构如图。
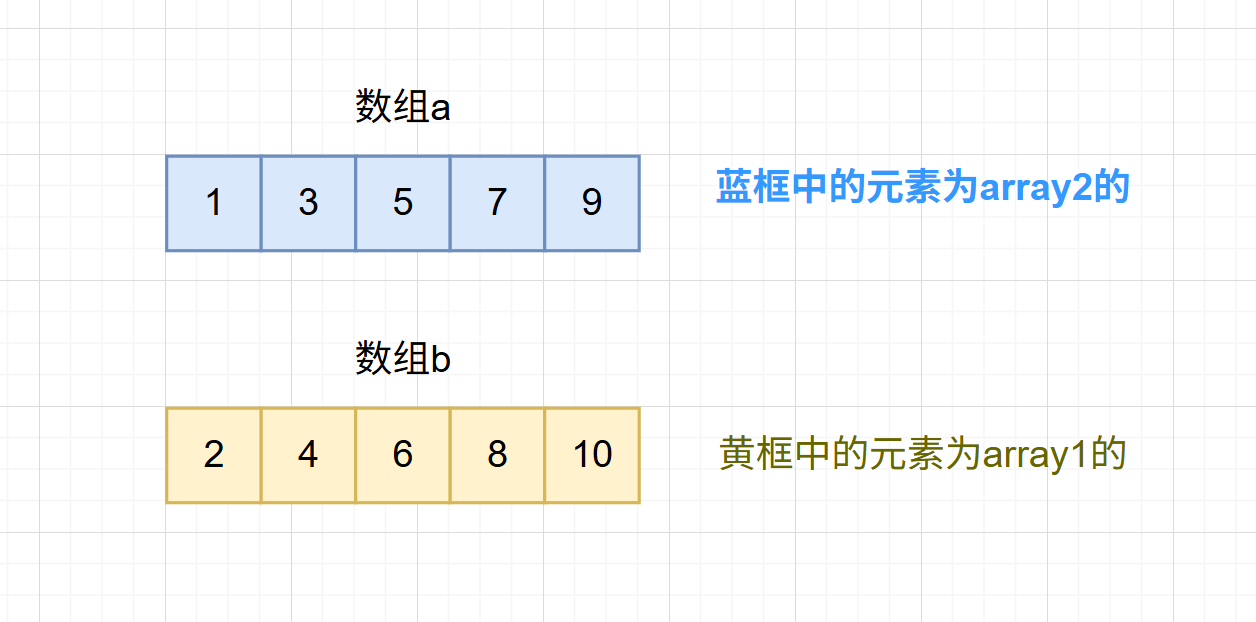
最终我们想要达到什么样的效果呢?

如图,我们要最后的结果为这样的,由图得array1末尾的元素为5,array2首位的元素为6,即可得中位数。
可以通过双指针法,在数组a、b中分别设立一个指针进行两个实际数组的值的比较。如果比较符合条件,就同步交换逻辑数组中的值。
指针i为数组a中有几个元素存储在array1中,指针j为数组b中有几个元素存储在array2中。最开始i = 0,j = (m + n + 1) / 2;
实际元素比较代码如下图。
while(true){if(a[i] <= b[j + 1] && a[i + 1] >= b[j]){int max1 = Math.max(a[i], b[j]);int min2 = Math.min(a[i + 1], b[j + 1]);return (m + n) % 2 > 0 ? max1 : (max1 + min2) / 2.0;}i++;j--;}a[i] <= b[j + 1]a[i]是数组a中当前划分点i右边的那个元素。b[j + 1]是数组b中当前划分点j右边的那个元素。- 这个条件确保了:
a数组划分到左边的部分,其最大值(a[i])不大于b数组划分到右边的部分的最小值(b[j + 1])。
a[i + 1] >= b[j]a[i + 1]是数组a中当前划分点i左边的那个元素。b[j]是数组b中当前划分点j左边的那个元素。- 这个条件确保了:
b数组划分到左边的部分,其最大值(b[j])不大于a数组划分到右边的部分的最小值(a[i + 1])。
当这两个条件同时满足时,意味着:
所有划分到 “左边” 的元素(a[0..i] 和 b[0..j])都小于或等于所有划分到 “右边” 的元素(a[i+1..m-1] 和 b[j+1..n-1])。
这正是我们想要的理想分割点!在这个分割点上,中位数就出现在 a[i], a[i+1], b[j], b[j+1] 这四个元素的附近。
这段代码的终止条件就是 if 条件判断成立。
这个 if 条件通过检查四个关键元素的大小关系,来确认是否找到了能将两个有序数组合并后正确分割出左右两部分的 “黄金分割点”。
一旦找到这个分割点,就可以根据合并后数组的总长度是奇数还是偶数,从这四个关键元素中计算出中位数并返回,从而终止循环。
为什么j 为(m + n + 1) / 2?
如果总长度为奇数的话,我们可以设定array1的末尾作为这个中位数,因此array1 默认要比 array2 大。
循环是否有越界风险?有没有可能结果在数组a、b末尾出现?
所以我们要在a、b数组的开头和结尾分别添加Integet.MIN_VALUE 和 Integer.MAX_VALUE。确保能够正确跳出循环。
整体流程图示



